On the Average Number of Octahedral Newforms of Prime Level
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Manjul Bhargava
The Work of Manjul Bhargava Manjul Bhargava's work in number theory has had a profound influence on the field. A mathematician of extraordinary creativity, he has a taste for simple problems of timeless beauty, which he has solved by developing elegant and powerful new methods that offer deep insights. When he was a graduate student, Bhargava read the monumental Disqui- sitiones Arithmeticae, a book about number theory by Carl Friedrich Gauss (1777-1855). All mathematicians know of the Disquisitiones, but few have actually read it, as its notation and computational nature make it difficult for modern readers to follow. Bhargava nevertheless found the book to be a wellspring of inspiration. Gauss was interested in binary quadratic forms, which are polynomials ax2 +bxy +cy2, where a, b, and c are integers. In the Disquisitiones, Gauss developed his ingenious composition law, which gives a method for composing two binary quadratic forms to obtain a third one. This law became, and remains, a central tool in algebraic number theory. After wading through the 20 pages of Gauss's calculations culminating in the composition law, Bhargava knew there had to be a better way. Then one day, while playing with a Rubik's cube, he found it. Bhargava thought about labeling each corner of a cube with a number and then slic- ing the cube to obtain 2 sets of 4 numbers. Each 4-number set naturally forms a matrix. A simple calculation with these matrices resulted in a bi- nary quadratic form. From the three ways of slicing the cube, three binary quadratic forms emerged. -

ICTS POSTER Outside Bangalore
T A T A I N S T I T U T E O F F U N D A M E N T A L R E S E A R C H A HOMI BHABHA BIRTH CENTENARY & ICTS INAUGURAL EVENT International Centre Theoretical Sciences science without bo28 Decemberun 2009d29 -a 31 Decemberri e2009s Satish Dhawan Auditorium Faculty Hall Indian Institute of Science, Bangalore. www.icts.res.in/program/icts-ie INVITED SPEAKERS / PANELISTS INCLUDE FOUNDATION STONE CEREMONY Siva Athreya ISI, Bangalore OF ICTS CAMPUS Naama Barkai Weizmann Institute The foundation stone will be unveiled by Manjul Bhargava Princeton University Prof. C N R Rao, FRS 4:00 pm, 28 December 2009 Édouard Brézin École Normale Supérieure Amol Dighe TIFR Michael Green DAMTP, Cambridge Chandrashekhar Khare UCLA Yamuna Krishnan NCBS-TIFR Lyman Page Princeton University Jaikumar Radhakrishnan TIFR C. S. Rajan TIFR Sriram Ramaswamy IISc G. Rangarajan IISc C. N. R. Rao JNCASR Subir Sachdev Harvard University K. Sandeep CAM-TIFR Sriram Shastry UC Santa Cruz PUBLIC LECTURES Ashoke Sen HRI J. N. Tata Auditorium, IISc (FREE AND OPEN TO ALL) Anirvan Sengupta Rutgers University K. R. Sreenivasan Abdus Salam ICTP Michael Atiyah University of Edinburgh Andrew Strominger Harvard University Truth and Beauty in Mathematics and Physics 5:30 pm, 27 December 2009 Raman Sundrum Johns Hopkins University Ajay Sood IISc David Gross KITP, Santa Barbara The Role of Theory in Science Tarun Souradeep IUCAA 5:30 pm, 28 December 2009 Eitan Tadmor University of Maryland Albert Libchaber Rockefeller University Sandip Trivedi TIFR The Origin of Life: from Geophysics to Biology? Mukund Thattai NCBS-TIFR 5:30 pm, 30 December 2009 S. -

Dear Aspirant with Regard
DEAR ASPIRANT HERE WE ARE PRESENTING YOU A GENRAL AWERNESS MEGA CAPSULE FOR IBPS PO, SBI ASSOT PO , IBPS ASST AND OTHER FORTHCOMING EXAMS WE HAVE UNDERTAKEN ALL THE POSSIBLE CARE TO MAKE IT ERROR FREE SPECIAL THANKS TO THOSE WHO HAS PUT THEIR TIME TO MAKE THIS HAPPEN A IN ON LIMITED RESOURCE 1. NILOFAR 2. SWETA KHARE 3. ANKITA 4. PALLAVI BONIA 5. AMAR DAS 6. SARATH ANNAMETI 7. MAYANK BANSAL WITH REGARD PANKAJ KUMAR ( Glory At Anycost ) WE WISH YOU A BEST OF LUCK CONTENTS 1 CURRENT RATES 1 2 IMPORTANT DAYS 3 CUPS & TROPHIES 4 4 LIST OF WORLD COUNTRIES & THEIR CAPITAL 5 5 IMPORTANT CURRENCIES 9 6 ABBREVIATIONS IN NEWS 7 LISTS OF NEW UNION COUNCIL OF MINISTERS & PORTFOLIOS 13 8 NEW APPOINTMENTS 13 9 BANK PUNCHLINES 15 10 IMPORTANT POINTS OF UNION BUDGET 2012-14 16 11 BANKING TERMS 19 12 AWARDS 35 13 IMPORTANT BANKING ABBREVIATIONS 42 14 IMPORTANT BANKING TERMINOLOGY 50 15 HIGHLIGHTS OF UNION BUDGET 2014 55 16 FDI LLIMITS 56 17 INDIAS GDP FORCASTS 57 18 INDIAN RANKING IN DIFFERENT INDEXS 57 19 ABOUT : NABARD 58 20 IMPORTANT COMMITTEES IN NEWS 58 21 OSCAR AWARD 2014 59 22 STATES, CAPITAL, GOVERNERS & CHIEF MINISTERS 62 23 IMPORTANT COMMITTEES IN NEWS 62 23 LIST OF IMPORTANT ORGANIZATIONS INDIA & THERE HEAD 65 24 LIST OF INTERNATIONAL ORGANIZATIONS AND HEADS 66 25 FACTS ABOUT CENSUS 2011 66 26 DEFENCE & TECHNOLOGY 67 27 BOOKS & AUTHOURS 69 28 LEADER”S VISITED INIDIA 70 29 OBITUARY 71 30 ORGANISATION AND THERE HEADQUARTERS 72 31 REVOLUTIONS IN AGRICULTURE IN INDIA 72 32 IMPORTANT DAMS IN INDIA 73 33 CLASSICAL DANCES IN INDIA 73 34 NUCLEAR POWER -

International Conference on Number Theory and Discrete Mathematics (ONLINE) (ICNTDM) 11 - 14, DECEMBER-2020
International Conference on Number Theory and Discrete Mathematics (ONLINE) (ICNTDM) 11 - 14, DECEMBER-2020 Organised by RAMANUJAN MATHEMATICAL SOCIETY Hosted by DEPARTMENT OF MATHEMATICS RAJAGIRI SCHOOL OF ENGINEERING & TECHNOLOGY (AUTONOMOUS) Kochi, India International Conference on Number Theory and Discrete Mathematics PREFACE The International Conference on Number Theory and Discrete Mathematics (ICNTDM), organised by the Ramanujan Mathematical Society (RMS), and hosted by the Rajagiri School of Engineering and Technology (RSET), Cochin is a tribute to the legendary Indian mathematician Srinivasa Ramanujan who prematurely passed away a hundred years ago on 26th April 1920 leaving a lasting legacy. Conceived as any usual conference as early as June 2019, the ICNTDM was compelled to switch to online mode due to the pandemic, like most events round the globe this year. The International Academic Programme Committee, consisting of distinguished mathematicians from India and abroad, lent us a helping hand every possible way, in all aspects of the conference. As a result, we were able to evolve a strong line up of reputed speakers from India, Austria, Canada, China, France, Hungary, Japan, Russia, Slovenia, UK and USA, giving 23 plenary talks and 11 invited talks, in addition to the 39 speakers in the contributed session. This booklet consists of abstracts of all these talks and two invited articles; one describing the various academic activities that RMS is engaged in, tracing history from its momentous beginning in 1985, and a second article on Srinivasa Ramanujan. It is very appropriate to record here that, in conjunction with the pronouncement of the year 2012 { the 125th birth anniversary year of Ramanujan { as the `National Mathematics Year', RMS heralded an excellent initiative of translating the cele- brated book `The Man Who Knew Infinity' into many Indian languages. -

Manjul Bhargava** Princeton University on Sums of Squares and the "290 Theorem"
[POSTER] University of Florida, Mathematics Department FIRST RAMANUJAN* COLLOQUIUM by Professor Manjul Bhargava** Princeton University on Sums of squares and the "290 theorem" Date and Time: 4:00 - 5:00pm, Monday, March 19, 2007 Room: FAB 103 Refreshments: After the lecture in the Atrium (LIT 339) OPENING REMARKS by George E. Andrews*** Evan Pugh Professor - Penn. State Univ. Distinguished Visiting Professor - UF Abstract: The famous "Four Squares Theorem" of Lagrange asserts that any positive integer can be expressed as the sum of four square numbers. That is, the quadratic form a2 + b2 + c2 + d2 represents all (positive) integers. When does a general quadratic form represent all integers? When does it represent all odd integers? When does it represent all primes? We show how all these questions turn out to have very simple and surprising answers. In particular, we describe the recent work (joint with Jonathan Hanke, Duke University) in proving Conway's "290-Conjecture". This solves a problem of Ramanujan on quadratic forms. THREE MATHEMATICS SEMINAR TALKS Following the Colloquium, Professor Bhargava will give three seminar talks. The three seminars will work towards a precise statement and proof of Ramanujan's quaternary problem and Conway's 290- Conjecture. JOINT NUMBER THEORY & COMBINATORICS SEMINARS on 1. The arithmetic of quadratic forms: an overview Tue, Mar 20, at 12:50 pm in LIT 339 2. Ramanujan's quaternary problem and finiteness theorems for quadratic forms Tue, Mar 20, at 1:55 pm in LIT 339 3. Effective finiteness theorems and the proof of Conway's 290- conjecture Wed, Mar 21, at 3:00 pm in LIT 339 * ABOUT RAMANUJAN: Srinivasa Ramanujan (1887-1920), a self-taught genius from South India, dazzled mathematicians at Cambridge University by communicating bewildering formulae in a series of letters. -

Math Student 2007
ISSN: 0025-5742 THE MATHEMATICS STUDENT Volume 76, Numbers 1 - 4, (2007) copy- Edited by J. R. PATADIA circulation (Issued: October, 2008) Member'sfor not PUBLISHED BY THE INDIAN MATHEMATICAL SOCIETY (In the memory of late Professor M. K. Singal) THE MATHEMATICS STUDENT Edited by J. R. PATADIA In keeping with the current periodical policy, THE MATHEMATICS STUDENT (STUDENT) will seek to publish material of interest not just to mathematicians with specialized interest but to undergraduate and postgraduate students and teachers of mathematics in India. With this in view, it will publish material of the following type: 1. Expository articles and popular (not highly technical) articles. 2. Classroom notes (this can include hints on teaching certain topics or filling vital gaps in the usual treatments of topics to be found in text-books or how some execises can and should be made an integral part of teaching, etc.) 3. Problems and solutions, News and Views. 4. Information on articles of common interest published in other periodicals, 5. Proceedings of IMS Conferences. Expository articles, classroom notes, news and announcements and research papers are invited for publication in THE MATHEMATICS STUDENT. Manuscripts intended for publication should preferably be submitted online in the LaTeX .pdf file or in the standard word processing format (Word or Word Perfect) including figures and tables. In case of hard copy submission, three copies of the manuscripts along with the Compact Disc (CD) copy should be submitted to the Editor Dr. J. R. Patadia, Department of Mathematics, faculty of Science, The Maharaja Sayajirao University of Baroda, Vadodara-390 002 (Gujarat),copy- India. -

37Th ANNUAL REPORT
UNIVERSITY OF HYDERABAD 37th ANNUAL REPORT Report on the working of the University (1 April 2011 to 31 March 2012) Prof. C. R. Rao Road Central University P.O. Gachibowli, Hyderabad – 500 046 www.uohyd.ac.in beforePages.indd 1 2/20/2013 6:59:11 PM Our Motto forms part of a verse appearing in Vishnu-Purana (1.19.41) The whole verse reads as follows : The verse also occurs in the anthology of subhasitas entitled "Sarangadharapaddhati" (No.4396). In this latter work, the source of the verse is given as Vasisthat. The verse obviously possesses an ethical-spiritual import and may be translated as follows: “That is (right) action which does not conduce to bondage (Karmabandha in the Bhagavadgita sense); that is (true) knowledge which conduces to final liberation or spiritual emancipation; (any) other knowledge implies mere skill in craft beforePages.indd 2 2/20/2013 6:59:12 PM Visitor The President of India Chief Rector The Governor of Andhra Pradesh Chancellor R Chidambaram (upto 11.01.2012) C H Hanumantha Rao (12.01.2012) Vice-Chancellor Ramakrishna Ramaswamy Pro Vice-Chancellor E. Haribabu Deans of Schools Mathematics & C.I.S. T Amaranath, Ph.D. (I.I.T., Madras) Physics C Bansal, Ph.D. (TIFR., Bombay) Chemistry M V Rajasekharan, Ph.D.(IIT, Madras) Life Sciences M Ramanadham, Ph.D. (OU, Hyderabad) Humanities Mohan G Ramanan, Ph.D. (BITS, Pilani) Social Sciences G Nancharaiah, Ph.D. (AU, Visakhapatnam) Sarojini Naidu School of Vinod Pavarala, Ph.D. (University of Pittsburgh) Arts and Communication (upto 18.03.2012) B Anandhakrishnan, Ph.D. -
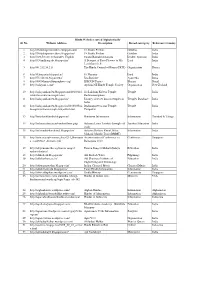
1.Hindu Websites Sorted Alphabetically
Hindu Websites sorted Alphabetically Sl. No. Website Address Description Broad catergory Reference Country 1 http://18shaktipeetasofdevi.blogspot.com/ 18 Shakti Peethas Goddess India 2 http://18shaktipeetasofdevi.blogspot.in/ 18 Shakti Peethas Goddess India 3 http://199.59.148.11/Gurudev_English Swami Ramakrishnanada Leader- Spiritual India 4 http://330milliongods.blogspot.in/ A Bouquet of Rose Flowers to My Lord India Lord Ganesh Ji 5 http://41.212.34.21/ The Hindu Council of Kenya (HCK) Organisation Kenya 6 http://63nayanar.blogspot.in/ 63 Nayanar Lord India 7 http://75.126.84.8/ayurveda/ Jiva Institute Ayurveda India 8 http://8000drumsoftheprophecy.org/ ISKCON Payers Bhajan Brazil 9 http://aalayam.co.nz/ Ayalam NZ Hindu Temple Society Organisation New Zealand 10 http://aalayamkanden.blogspot.com/2010/11/s Sri Lakshmi Kubera Temple, Temple India ri-lakshmi-kubera-temple.html Rathinamangalam 11 http://aalayamkanden.blogspot.in/ Journey of lesser known temples in Temples Database India India 12 http://aalayamkanden.blogspot.in/2010/10/bra Brahmapureeswarar Temple, Temple India hmapureeswarar-temple-tirupattur.html Tirupattur 13 http://accidentalhindu.blogspot.in/ Hinduism Information Information Trinidad & Tobago 14 http://acharya.iitm.ac.in/sanskrit/tutor.php Acharya Learn Sanskrit through self Sanskrit Education India study 15 http://acharyakishorekunal.blogspot.in/ Acharya Kishore Kunal, Bihar Information India Mahavir Mandir Trust (BMMT) 16 http://acm.org.sg/resource_docs/214_Ramayan An international Conference on Conference Singapore -

Alphabetical List of Persons for Whom Recommendations Were Received for Padma Awards - 2015
Alphabetical List of Persons for whom recommendations were received for Padma Awards - 2015 Sl. No. Name 1. Shri Aashish 2. Shri P. Abraham 3. Ms. Sonali Acharjee 4. Ms. Triveni Acharya 5. Guru Shashadhar Acharya 6. Shri Gautam Navnitlal Adhikari 7. Dr. Sunkara Venkata Adinarayana Rao 8. Shri Pankaj Advani 9. Shri Lal Krishna Advani 10. Dr. Devendra Kumar Agarwal 11. Shri Madan Mohan Agarwal 12. Dr. Nand Kishore Agarwal 13. Dr. Vinay Kumar Agarwal 14. Dr. Shekhar Agarwal 15. Dr. Sanjay Agarwala 16. Smt. Raj Kumari Aggarwal 17. Ms. Preety Aggarwal 18. Dr. S.P. Aggarwal 19. Dr. (Miss) Usha Aggarwal 20. Shri Vinod Aggarwal 21. Shri Jaikishan Aggarwal 22. Dr. Pratap Narayan Agrawal 23. Shri Badriprasad Agrawal 24. Dr. Sudhir Agrawal 25. Shri Vishnu Kumar Agrawal 26. Prof. (Dr.) Sujan Agrawal 27. Dr. Piyush C. Agrawal 28. Shri Subhash Chandra Agrawal 29. Dr. Sarojini Agrawal 30. Shri Sushiel Kumar Agrawal 31. Shri Anand Behari Agrawal 32. Dr. Varsha Agrawal 33. Dr. Ram Autar Agrawal 34. Shri Gopal Prahladrai Agrawal 35. Shri Anant Agrawal 36. Prof. Afroz Ahmad 37. Prof. Afzal Ahmad 38. Shri Habib Ahmed 39. Dr. Siddeek Ahmed Haji Panamtharayil 40. Dr. Ranjan Kumar Akhaury 41. Ms. Uzma Akhtar 42. Shri Eshan Akhtar 43. Shri Vishnu Akulwar 44. Shri Bruce Alberts 45. Captain Abbas Ali 46. Dr. Mohammed Ali 47. Dr. Govardhan Aliseri 48. Dr. Umar Alisha 49. Dr. M. Mohan Alva 50. Shri Mohammed Amar 51. Shri Gangai Amaren 52. Smt. Sindhutai Ramchandra Ambike 53. Mata Amritanandamayi 54. Dr. Manjula Anagani 55. Shri Anil Kumar Anand 56. -

INFOSYS PRIZE 2012 “There Are Two Kinds of Truth: the Truth That Lights the Way and the Truth That Warms the Heart
Dr. Ashish Lele Engineering and Computer Science Prof. Sanjay Subrahmanyam Prof. Amit Chaudhuri Humanities – History Humanities – Literary Studies Prof. Satyajit Mayor Life Sciences Prof. Manjul Bhargava Dr. A. Ajayaghosh Mathematical Sciences Physical Sciences Prof. Arunava Sen Social Sciences – Economics INFOSYS SCIENCE FOUNDATION INFOSYS SCIENCE FOUNDATION Infosys Campus, Electronics City, Hosur Road, Bangalore 560 100 Tel: 91 80 2852 0261 Fax: 91 80 2852 0362 Email: [email protected] www.infosys-science-foundation.com INFOSYS PRIZE 2012 “There are two kinds of truth: The truth that lights the way and the truth that warms the heart. The first of these is science, and the second is art. Neither is independent of the other or more important than the other. Without art science would be as useless as a pair of high forceps in the hands of a plumber. Without science art would become a crude mess of folklore and emotional quackery. The truth of art keeps science from becoming inhuman, and the truth of science keeps art from becoming ridiculous.” Raymond Chandler 1888 – 1959 Author Engineering and Computer Science The Infosys Prize for Engineering and Computer Science is awarded to Doctor Ashish Lele for his incisive contributions in molecular tailoring of stimuli responsive smart polymeric gels; exploring the anomalous behavior Dr. Ashish Lele of rheologically complex fluids and for building the Scientist, National Chemical Laboratories (NCL), bridge between macromolecular dynamics and polymer Pune, India processing. Ashish Lele is a Scientist at the Scope and impact of work processes, which often limits industrial National Chemical Laboratories production. (NCL), Pune, India. He The thrust of Dr. -
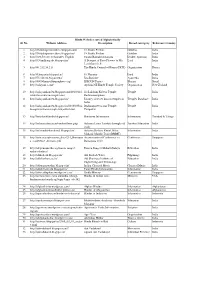
Hindu Websites Sorted Alphabetically Sl
Hindu Websites sorted Alphabetically Sl. No. Website Address Description Broad catergory Reference Country 1 http://18shaktipeetasofdevi.blogspot.com/ 18 Shakti Peethas Goddess India 2 http://18shaktipeetasofdevi.blogspot.in/ 18 Shakti Peethas Goddess India 3 http://199.59.148.11/Gurudev_English Swami Ramakrishnanada Leader- Spiritual India 4 http://330milliongods.blogspot.in/ A Bouquet of Rose Flowers to My Lord India Lord Ganesh Ji 5 http://41.212.34.21/ The Hindu Council of Kenya (HCK) Organisation Kenya 6 http://63nayanar.blogspot.in/ 63 Nayanar Lord India 7 http://75.126.84.8/ayurveda/ Jiva Institute Ayurveda India 8 http://8000drumsoftheprophecy.org/ ISKCON Payers Bhajan Brazil 9 http://aalayam.co.nz/ Ayalam NZ Hindu Temple Society Organisation New Zealand 10 http://aalayamkanden.blogspot.com/2010/11/s Sri Lakshmi Kubera Temple, Temple India ri-lakshmi-kubera-temple.html Rathinamangalam 11 http://aalayamkanden.blogspot.in/ Journey of lesser known temples in Temples Database India India 12 http://aalayamkanden.blogspot.in/2010/10/bra Brahmapureeswarar Temple, Temple India hmapureeswarar-temple-tirupattur.html Tirupattur 13 http://accidentalhindu.blogspot.in/ Hinduism Information Information Trinidad & Tobago 14 http://acharya.iitm.ac.in/sanskrit/tutor.php Acharya Learn Sanskrit through self Sanskrit Education India study 15 http://acharyakishorekunal.blogspot.in/ Acharya Kishore Kunal, Bihar Information India Mahavir Mandir Trust (BMMT) 16 http://acm.org.sg/resource_docs/214_Ramayan An international Conference on Conference Singapore -

Mathematical Olympiad & Other Scholarship, Research Programmes
DEPARTMENT OF MATHEMATICS COCHIN UNIVERSITY OF SCIENCE AND TECHNOLOGY COCHIN - 682 022 The erstwhile University of Cochin founded in 1971 was reorganised and converted into a full fledged University of Science and Technology in 1986 for the promotion of Graduate and Post Graduate studies and advanced research in Applied Sciences, Technology, Commerce, Management and Social Sciences. The combined Department of Mathematics and Statistics came into existence in 1976, which was bifurcated to form the Department of Mathematics in 1996. Apart from offering M.Sc, and M. Phil. degree courses in Mathematics it has active research programmes in, Algebra, Operations Research, Stochastic Processes, Graph Theory, Wavelet Analysis and Operator Theory. The Department has been coordinating the Mathematical olympiad - a talent search programme for high school students since 1990. It also organizes Mathematics Enrichment Programmes for students and teachers to promote the cause of Mathematics and attract young minds to choose a career in Mathematics. It also co-ordinates the national level tests of NBHM for M.Sc and Ph.D scholarship. The department also organized the ‘International Conference on Recent Trends in Graph Theory and Combinatorics’ as a satellite conference of the International Congress of Mathematicians (ICM) during August 2010. “Tejasvinavadhithamastu” May learning illumine us both, The teacher and the taught. In the ‘SILVER JUBILEE YEAR’ of the RMO Co-ordination, we plan a reunion of the ‘INMO Awardees’ during 1991-2014. Please contact the Regional Co-ordinator ([email protected].) -1- PREFACE This brochure contains information on various talent search and research programmes in basic sciences in general and mathematics in particular and is meant for the students of Xth standard and above.