Local Lunar Gravity Field Analysis Over the South Poleaitken Basin from SELENE Farside Tracking Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Daily Iowan (Iowa City, Iowa), 1953-10-22
The Weather Serving the State Partb c10., aDd eeoIH ·versity of Iowa toda,. CleariDc ....... Art slderlbb eooIer FrWar. Campus and JII,h ~aJ. T.; 1_. 52; Hla'h WednH41a7. II; low. he SUI art i.:wa City 67. attend the 1868 - A,P Leased Wile, Wirephot.o - Five Cent. Iowa City, Iowa, Thursday, Oct. 22, 1953 - Vol. 97, No. 276 the found- , Eat. College Art • ~---------------------------------------------- Department orlSin. Mln ./ '0 the rti.t trom .ohio the conter- ~ shown by ueen ·Will· Open Homecoming ence df 1he AcsthetJcs ege in. No- • Homecoming Mums Aqui Show To Feature Five Iowa sportscasters and Qne ------------ Varied Acts sports writer will judge the utes past any given point In the beauty, or~inallty and humor ot parade route. The 40 tloats wiU Three days ot 1953 Homecom , ' the I10nt entries In the fifth an- then move to the area just east In, frolic will let the ful\-steam- nual SUI Homecoming parade Frl- of Iowa stadium to remain throu,ll abead si,nal tonight when one ot day night at 7. Saturday's game as a post-parade Taking time out from their re- dISplay parade chairman Loren five campus lovelies is named porting responsibilities to score Hlcker ~on lays. Dolphin Queen for SUY'! 31st an- each of 40 floats ror beaut), will . nUIII poolsld~ sholl'. be Gene Claussen, KXIC Iowa Musical marching grou~s In the City and Gene Shumate KSO De parade will total 13, With nine Pre!\Cntatlon of the qucen-ror- Moines. • high school bands, Shriner bands a-weekend will come at 8 p.m. -
Association of Unit Owners Contact List
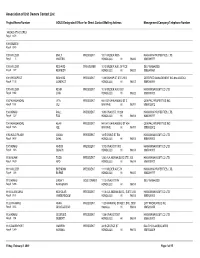
Association of Unit Owners Contact List Project Name/Number AOUO Designated Officer for Direct Contact/Mailing Address Management Company/Telephone Number `AKOKO AT HO`OPILI Reg.# 8073 1001 QUEEN Reg.# 7675 1001 WILDER EMILY PRESIDENT 1001 WILDER #305 HAWAIIAN PROPERTIES, LTD. Reg.# 5 WATERS HONOLULU HI 96822 8085399777 1010 WILDER RICHARD TREASURER 1010 WILDER AVE, OFFICE SELF MANAGED Reg.# 377 KENNEDY HONOLULU HI 96822 8085241961 1011 PROSPECT RICHARD PRESIDENT 1188 BISHOP ST STE 2503 CERTIFIED MANAGEMENT INC dba ASSOCI Reg.# 1130 CONRADT HONOLULU HI 96813 8088360911 1015 WILDER KEVIN PRESIDENT 1015 WILDER AVE #201 HAWAIIANA MGMT CO LTD Reg.# 1960 LIMA HONOLULU HI 96822 8085939100 1037 KAHUAMOKU VITA PRESIDENT 94-1037 KAHUAMOKU ST 3 CEN PAC PROPERTIES INC Reg.# 1551 VILI WAIPAHU HI 96797 8085932902 1040 KINAU PAUL PRESIDENT 1040 KINAU ST., #1206 HAWAIIAN PROPERTIES, LTD. Reg.# 527 FOX HONOLULU HI 96814 8085399777 1041 KAHUAMOKU ALAN PRESIDENT 94-1041 KAHUAMOKU ST 404 CEN PAC PROPERTIES INC Reg.# 1623 IGE WAIPAHU HI 96797 8085932902 1054 KALO PLACE JUANA PRESIDENT 1415 S KING ST 504 HAWAIIANA MGMT CO LTD Reg.# 5450 DAHL HONOLULU HI 96814 8085939100 1073 KINAU ANSON PRESIDENT 1073 KINAU ST 1003 HAWAIIANA MGMT CO LTD Reg.# 616 QUACH HONOLULU HI 96814 8085939100 1108 AUAHI TODD PRESIDENT 1240 ALA MOANA BLVD STE. 200 HAWAIIANA MGMT CO LTD Reg.# 7429 APO HONOLULU HI 96814 8085939100 1111 WILDER BRENDAN PRESIDENT 1111 WILDER AVE 7A HAWAIIAN PROPERTIES, LTD. Reg.# 228 BURNS HONOLULU HI 96822 8085399777 1112 KINAU LINDA Y SOLE OWNER 1112 KINAU ST PH SELF MANAGED Reg.# 1295 NAKAGAWA HONOLULU HI 96814 1118 ALA MOANA NICHOLAS PRESIDENT 1118 ALA MOANA BLVD., SUITE 200 HAWAIIANA MGMT CO LTD Reg.# 7431 VANDERBOOM HONOLULU HI 96814 8085939100 1133 WAIMANU ANNA PRESIDENT 1133 WAIMANU STREET, STE. -

Martian Crater Morphology
ANALYSIS OF THE DEPTH-DIAMETER RELATIONSHIP OF MARTIAN CRATERS A Capstone Experience Thesis Presented by Jared Howenstine Completion Date: May 2006 Approved By: Professor M. Darby Dyar, Astronomy Professor Christopher Condit, Geology Professor Judith Young, Astronomy Abstract Title: Analysis of the Depth-Diameter Relationship of Martian Craters Author: Jared Howenstine, Astronomy Approved By: Judith Young, Astronomy Approved By: M. Darby Dyar, Astronomy Approved By: Christopher Condit, Geology CE Type: Departmental Honors Project Using a gridded version of maritan topography with the computer program Gridview, this project studied the depth-diameter relationship of martian impact craters. The work encompasses 361 profiles of impacts with diameters larger than 15 kilometers and is a continuation of work that was started at the Lunar and Planetary Institute in Houston, Texas under the guidance of Dr. Walter S. Keifer. Using the most ‘pristine,’ or deepest craters in the data a depth-diameter relationship was determined: d = 0.610D 0.327 , where d is the depth of the crater and D is the diameter of the crater, both in kilometers. This relationship can then be used to estimate the theoretical depth of any impact radius, and therefore can be used to estimate the pristine shape of the crater. With a depth-diameter ratio for a particular crater, the measured depth can then be compared to this theoretical value and an estimate of the amount of material within the crater, or fill, can then be calculated. The data includes 140 named impact craters, 3 basins, and 218 other impacts. The named data encompasses all named impact structures of greater than 100 kilometers in diameter. -

Planetary Constants and Models
JPL D-12947 PF-IOO-PMC-01 Mars Pathfinder ProJect PLANETARY CONSTANTS AND MODELS Mars at Launch Earth at La_ Dec 2, 1996 SunI, Earth at Mars at Aniva July 4, 1997 December 1995 JilL Jet Propulsion Laboratory California Institute of Technology Pasadena, California JPL D-I2947 PF-IOO-PMC-OI Mars Pathfinder Project PLANETARY CONSTANTS AND MODELS Prepared by: ' Robin Vaughan December 1995 JPL Jet Propulsion Laboratory California Institute of Technology Pasadena, California JPL D-12947 PFolOO-PMCoO1 Revision History Date Changes Status 10/95 Issued preliminary version for review by project person-el Draft 12/95 First official release; incorporated comments from prelimi- Final nary review. JPL D- !294 7 PFo 100-PMCo 01 Contents List of Figures V 4 List of Tables vii List of Acronyms and Abbreviations ix INTRODUCTION 1 1.1 Purpose ............ .......................... 1 1.2 Scope .................... ................... 1 2 COORDINATE SYSTEMS 3 2.1 Definitions 2.1.1 Frame • " • • • ° * ° • " ° • * • ° ° " ° ° * ° • • • ° " " " ' • • • • • • 3 2.1.2 Center • " " • ° " " " ' ° ° ° • * " • • " • " • • " • " " " ° • ° • • • . • 6 2.1.3 Type .................................... 7 2.2 Celestial Systems . ; ............................. 7 2.2.1 The Inertial Reference Frames ..................... 8 2.2.2 Sun-Centered Systems .......................... 9 2.2.3 Earth-Centered Systems ......................... 9 2.2.4 Mars-Centered Systems ......................... 11 2.2.5 Spacecraft-CenteredSystems ...................... 16 2.2.6 MiscellaneousSystems -

In Pdf Format
lós 1877 Mik 88 ge N 18 e N i h 80° 80° 80° ll T 80° re ly a o ndae ma p k Pl m os U has ia n anum Boreu bal e C h o A al m re u c K e o re S O a B Bo l y m p i a U n d Planum Es co e ria a l H y n d s p e U 60° e 60° 60° r b o r e a e 60° l l o C MARS · Korolev a i PHOTOMAP d n a c S Lomono a sov i T a t n M 1:320 000 000 i t V s a Per V s n a s l i l epe a s l i t i t a s B o r e a R u 1 cm = 320 km lkin t i t a s B o r e a a A a A l v s l i F e c b a P u o ss i North a s North s Fo d V s a a F s i e i c a a t ssa l vi o l eo Fo i p l ko R e e r e a o an u s a p t il b s em Stokes M ic s T M T P l Kunowski U 40° on a a 40° 40° a n T 40° e n i O Va a t i a LY VI 19 ll ic KI 76 es a As N M curi N G– ra ras- s Planum Acidalia Colles ier 2 + te . -

Risks and Benefits of Fish Consumption
Rapport 12 − 2007 Risks and Benefits of Fish Consumption A Risk-Benefit Analysis Based on the Occurrence of Dioxin/PCB, Methyl Mercury, n-3 Fatty Acids and Vitamin D in Fish by W Becker, P O Darnerud and K Petersson-Grawé LIVSMEDELS VERKET NATIONAL FOOD ADMINISTRATION, Sweden � Produktion: Livsmedelsverkets rapportserie är avsedd för publicering Livsmedelsverket, Box 622 av projektrapporter, metodprövningar, utredningar m m. SE-751 26 Uppsala, Sweden I serien ingår även reserapporter och konferensmaterial. Teknisk redaktör: För innehållet svarar författarna själva. M Olausson Rapporterna utges i varierande upplagor och tilltrycks Tryck: i mån av efterfrågan. De kan rekvireras från Livsmedels- Kopieringshuset, Uppsala verkets kundtjänst (tel 018-17 55 06) till självkostnadspris (kopieringskostnad + expeditionsavgift). Uppsala 2008-01-07 Abbreviations/Glossary........................................................................................... 3 Preface..................................................................................................................... 5 Summary ................................................................................................................. 6 Overall conclusions............................................................................................. 6 Consumption of fish in Sweden.......................................................................... 8 Content of nutrients and environmental pollutants ............................................. 8 Quantitative risk-benefit -

(Iowa City, Iowa), 1964-06-25
city, ".-W.... cfay, JIIIII 24, '* ed Into the /lecond round by d& feating Heathet Cheadle of Britain, 7·5, 6-1. Warmer MNtty '*' 1M ,........: TO AAU FINALS- Warmer f.!MIt ." ........, ....... NEW BRUNSWICK, N.J. ttl - .. fl. Pertly c'-'r MIll ...., The top college broad jumpe~, ail owan w_ flrWey. Gayle Hopkins oC Arizona, and a Serving the State University of ICHDtJ and 1M Peopl8 of 10W4 CU~ pole vaulter who has cleared 1~ Ceet, Ohio State's Bob Neutzling, Jon CIty, [ -11wrIda.y, JUDe 15, 11M were added Tuesday to the field Cor this weekend's National AAU track championships, Other Asians Grave- Viet Ham Strong Man Backs .Ambassador Shift by U,S. Dulles in Jackson; AIGO " lai. Cl'O. ~uyen t..1}anh, r dil amba d • id Wedn day th am' unti.commu- WANTED NAACP Demonstration ni. t war i at hand, 'The frc world (; untri· ar right at our ' d,~ tJ) • ~troog RIDERS Marlon to Iowa City. MondlY throuib Saturday. 337·1356. Carol Altorlley Gener.al Robert K.nnedy sh.ak~~ hallds Wednesday with man premier told his people in Potter. 8-2( ... ... memb.rs of the National Au.cialion fOl' the Adv.nc.ment of e.l· a peech at R cb Ola, on the Gulf . MALE ROOMMATE to share new ored People. He greeted th.m during • m.rch .t the Department of Thailand. "and If necessary will aparlment. Preter grad student. Call tackle the problem of communism 337·7271 before noon. 8-2S of Justke in silent protest over the disappearance IIf thrft Y""" U_S. -

Tip-Enhanced Laser Ablation Sample Transfer for Mass Spectrometry
Louisiana State University LSU Digital Commons LSU Doctoral Dissertations Graduate School 2016 Tip-Enhanced Laser Ablation Sample Transfer for Mass Spectrometry Chinthaka Aravinda Seneviratne Louisiana State University and Agricultural and Mechanical College, [email protected] Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_dissertations Part of the Chemistry Commons Recommended Citation Seneviratne, Chinthaka Aravinda, "Tip-Enhanced Laser Ablation Sample Transfer for Mass Spectrometry" (2016). LSU Doctoral Dissertations. 2355. https://digitalcommons.lsu.edu/gradschool_dissertations/2355 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Doctoral Dissertations by an authorized graduate school editor of LSU Digital Commons. For more information, please [email protected]. TIP-ENHANCED LASER ABLATION SAMPLE TRANSFER FOR MASS SPECTROMETRY A Dissertation Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Doctor of Philosophy in The Department of Chemistry by Chinthaka Aravinda Seneviratne M.S., Bucknell University, 2011 B.Sc., University of Kelaniya, 2008 May 2016 This dissertation is dedicated with love to my parents, Hector and Dayani Seneviratne my wife Sameera Herath and my little buddy Julian !. ii ACKNOWLEDGEMENTS First and foremost, I give glory to God. Without God’s blessings, none of this would have been possible. It is a great pleasure to offer my unbounding appreciation for all who have supported and guided me over the course my doctoral studies to the completion of this dissertation. I would like to thank my doctoral mentor, Dr. -

Pander Society Newsletter
Pander Society Newsletter S O E R C D I E N T A Y P 1 9 6 7 Compiled and edited by P.H. von Bitter and J. Burke PALAEOBIOLOGY DIVISION, DEPARTMENT OF NATURAL HISTORY, ROYAL ONTARIO MUSEUM, TORONTO, ON, CANADA M5S 2C6 Number 41 May 2009 www.conodont.net Webmaster Mark Purnell, University of Leicester 2 Chief Panderer’s Remarks May 1, 2009 Dear Colleagues: It is again spring in southern Canada, that very positive time of year that allows us to forget our winter hibernation & the climatic hardships endured. It is also the time when Joan Burke and I get to harvest and see the results of our winter labours, as we integrate all the information & contributions sent in by you (Thank You) into a new and hopefully ever better Newsletter. Through the hard work of editor Jeffrey Over, Paleontographica Americana, vol. no. 62, has just been published to celebrate the 40th Anniversary of the Pander Society and the 150th Anniversary of the first conodont paper by Christian Pander in 1856; the titles and abstracts are here reproduced courtesy of the Paleontological Research Institution in Ithica, N.Y. Glen Merrill and others represented the Pander Society at a conference entitled “Geologic Problem Solving with Microfossils”, sponsored by NAMS, the North American Micropaleontology Section of SEPM, in Houston, Texas, March 15-18, 2009; the titles of papers that dealt with or mentioned conodonts, are included in this Newsletter. Although there have been no official Pander Society meetings since newsletter # 40, a year ago, there were undoubtedly many unofficial ones; many of these would have been helped by suitable refreshments, the latter likely being the reason I didn’t get to hear about the meetings. -

Geographic Coordinate Systems, Datums, Spheroids, Prime Meridians, and Angular Units of Measure
Geographic coordinate systems, datums, spheroids, prime meridians, and angular units of measure Current as of ArcGIS version 9.3 Angular Units of Measure ArcSDE macro ArcObjects macro code name radians / unit PE_U_RADIAN esriSRUnit_Radian 9101 Radian 1.0 PE_U_DEGREE esriSRUnit_Degree 9102 Degree p/180 PE_U_MINUTE esriSRUnit_Minute 9103 Arc–minute (p/180)/60 PE_U_SECOND esriSRUnit_Second 9104 Arc–second (p/180)/3600 PE_U_GRAD esriSRUnit_Grad 9105 Grad p/200 PE_U_GON esriSRUnit_Gon 9106 Gon p/200 PE_U_MICRORADIAN esriSRUnit_Microradian 9109 Microradian 1.0E-6 PE_U_MINUTE_CENTESIMAL esriSRUnit_Minute_Centesimal 9112 Centesimal minute p/20000 PE_U_SECOND_CENTESIMAL esriSRUnit_Second_Centesimal 9113 Centesimal second p/2000000 PE_U_MIL_6400 esriSRUnit_Mil_6400 9114 Mil p/3200 Spheroids Macro Code Name a (m) 1/f esriSRSpheroid_Airy1830 7001 Airy 1830 6377563.396 299.3249646 esriSRSpheroid_ATS1977 7041 ATS 1977 6378135.0 298.257 esriSRSpheroid_Australian 7003 Australian National 6378160 298.25 esriSRSpheroid_AuthalicSphere 7035 Authalic sphere (WGS84) 6371000 0 esriSRSpheroid_AusthalicSphereArcInfo 107008 Authalic sph (ARC/INFO) 6370997 0 esriSRSpheroid_AusthalicSphere_Intl1924 7057 Authalic sph (Int'l 1924) 6371228 0 esriSRSpheroid_Bessel1841 7004 Bessel 1841 6377397.155 299.1528128 esriSRSpheroid_BesselNamibia 7006 Bessel Namibia 6377483.865 299.1528128 esriSRSpheroid_Clarke1858 7007 Clarke 1858 6378293.639 294.2606764 esriSRSpheroid_Clarke1866 7008 Clarke 1866 6378206.4 294.9786982 esriSRSpheroid_Clarke1866Michigan 7009 Clarke 1866 Michigan -

2021 Finalist Directory
2021 Finalist Directory April 29, 2021 ANIMAL SCIENCES ANIM001 Shrimply Clean: Effects of Mussels and Prawn on Water Quality https://projectboard.world/isef/project/51706 Trinity Skaggs, 11th; Wildwood High School, Wildwood, FL ANIM003 Investigation on High Twinning Rates in Cattle Using Sanger Sequencing https://projectboard.world/isef/project/51833 Lilly Figueroa, 10th; Mancos High School, Mancos, CO ANIM004 Utilization of Mechanically Simulated Kangaroo Care as a Novel Homeostatic Method to Treat Mice Carrying a Remutation of the Ppp1r13l Gene as a Model for Humans with Cardiomyopathy https://projectboard.world/isef/project/51789 Nathan Foo, 12th; West Shore Junior/Senior High School, Melbourne, FL ANIM005T Behavior Study and Development of Artificial Nest for Nurturing Assassin Bugs (Sycanus indagator Stal.) Beneficial in Biological Pest Control https://projectboard.world/isef/project/51803 Nonthaporn Srikha, 10th; Natthida Benjapiyaporn, 11th; Pattarapoom Tubtim, 12th; The Demonstration School of Khon Kaen University (Modindaeng), Muang Khonkaen, Khonkaen, Thailand ANIM006 The Survival of the Fairy: An In-Depth Survey into the Behavior and Life Cycle of the Sand Fairy Cicada, Year 3 https://projectboard.world/isef/project/51630 Antonio Rajaratnam, 12th; Redeemer Baptist School, North Parramatta, NSW, Australia ANIM007 Novel Geotaxic Data Show Botanical Therapeutics Slow Parkinson’s Disease in A53T and ParkinKO Models https://projectboard.world/isef/project/51887 Kristi Biswas, 10th; Paxon School for Advanced Studies, Jacksonville, -

Envision – Front Cover
EnVision – Front Cover ESA M5 proposal - downloaded from ArXiV.org Proposal Name: EnVision Lead Proposer: Richard Ghail Core Team members Richard Ghail Jörn Helbert Radar Systems Engineering Thermal Infrared Mapping Civil and Environmental Engineering, Institute for Planetary Research, Imperial College London, United Kingdom DLR, Germany Lorenzo Bruzzone Thomas Widemann Subsurface Sounding Ultraviolet, Visible and Infrared Spectroscopy Remote Sensing Laboratory, LESIA, Observatoire de Paris, University of Trento, Italy France Philippa Mason Colin Wilson Surface Processes Atmospheric Science Earth Science and Engineering, Atmospheric Physics, Imperial College London, United Kingdom University of Oxford, United Kingdom Caroline Dumoulin Ann Carine Vandaele Interior Dynamics Spectroscopy and Solar Occultation Laboratoire de Planétologie et Géodynamique Belgian Institute for Space Aeronomy, de Nantes, Belgium France Pascal Rosenblatt Emmanuel Marcq Spin Dynamics Volcanic Gas Retrievals Royal Observatory of Belgium LATMOS, Université de Versailles Saint- Brussels, Belgium Quentin, France Robbie Herrick Louis-Jerome Burtz StereoSAR Outreach and Systems Engineering Geophysical Institute, ISAE-Supaero University of Alaska, Fairbanks, United States Toulouse, France EnVision Page 1 of 43 ESA M5 proposal - downloaded from ArXiV.org Executive Summary Why are the terrestrial planets so different? Venus should be the most Earth-like of all our planetary neighbours: its size, bulk composition and distance from the Sun are very similar to those of Earth.