DOCSLIB.ORG

Thermoeconomic Analysis of EGS/Deep Geothermal Resources in the Region of Alsace, France

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Thermoeconomic Analysis of EGS/Deep Geothermal Resources in the Region of Alsace, France Thermoeconomic analysis of EGS/Deep Geothermal Resources in the region of Alsace, France Emmanuel Cabral Thesis of 60 ECTS credits Master of Science (MSc) in Sustainable Energy Engineering June 2018 ii Thermoeconomic analysis of EGS/Deep Geothermal Resources in the region of Alsace, France Thesis of 60 ECTS credits submitted to the School of Science and Engineering at Reykjavík University in partial fulfillment of the requirements for the degree of Master of Science (M.Sc.) in Sustainable Energy Engineering June 2018 Supervisors: Páll Valdimarsson, Supervisor Adjunct Professor, Reykjavík University, Iceland William S. Harvey, Advisor Visiting Professor, Reykjavík University, Iceland Examiner: Heimir Hjartarson, Examiner Geothermal Energy & District Heating Engineer, Efla Consulting Engineers, Iceland iv Copyright Emmanuel Cabral June 2018 vi Thermoeconomic analysis of EGS/Deep Geothermal Resources in the region of Alsace, France Emmanuel Cabral June 2018 Abstract Three geothermal projects in the region of Alsace are currently being developed and executed by the companies Fonroche Géothermie and L’Electricié de Strasbourg (ES). With the aim of exploiting the thermal energy stored at 5000 m below the surface of the earth, these projects foresee the implementation of one binary power plant, and two cogenerating units that will be integrated to the local grid, and benefit from European and national incentives for sustainable energy production. This research focuses on the utilization of the geothermal energy available in Vendenheim, Eckbolsheim, and Illkirch. Special emphasis is made on the first and largest project in the city of Vendenheim, where an industrial ecosystem is also defined, next to the proposed geothermal binary power plant. The research is structured in three main sections, two of which (Thermodynamics and Economics) constitute the main pillars of the thesis. The first chapter provides preliminary information, current operations, and data leading to the proposed cascading applications fit for the region such as beet sugar production, beer production, hop drying, microalgae production and drying, wine distillation, and two power production scenarios. The second chapter focuses on the thermodynamic analysis of a binary power plant and a Combined Heat and Power Plant in Vendenheim, analyzing the second law efficiency and exergy flow through the system, and providing insight on the proposed direct applications. Comparing the real efficiencies of a Combined Heat and Power system shows that the efficiencies decrease considerably when introducing a cascading scenario, 44,43% for a full power only subcritical binary plant and 24,43% for a Combined Heat and Power system. The full power production proposal is thus selected for a thermoeconomic analysis to review the feasibility of using the geothermal resource for power production only. In the third chapter, the thermoeconomic analysis is computed for the full power production scenario, analyzing balancing costs and exergoeconomic factors of the components resulting from the exergy flow through the system. The proposed subcritical power plant in Vendenheim produces 7,5 MW of work at the turbine, showing the project to be feasible at the current electricity selling rates in Alsace (200 – 246 €/MWh for projects under 12 MWe of capacity). The research presents cost flow analyses associated with irreversibilities, providing insight on potential improvements of the system. Irreversibilities within power plant could be reduced and optimized, making alternative or advanced binary plants additionally feasible than the proposed subcritical system. viii Thermoeconomic analysis of EGS/Deep Geothermal Resources in the region of Alsace, France. Emmanuel Cabral Thesis of 60 ECTS credits submitted to the School of Science and Engineering at Reykjavík University in partial fulfillment of the requirements for the degree of Master of Science (M.Sc.) in Sustainable Energy Engineering June 2018 Student: Emmanuel Cabral Supervisors: Páll Valdimarsson Examiner: Heimir Hjartarson x The undersigned hereby grants permission to the Reykjavík University Library to reproduce single copies of this Thesis entitled Thermoeconomic analysis of EGS/Deep Geothermal Resources in the region of Alsace, France and to lend or sell such copies for private, scholarly or scientific research purposes only. The author reserves all other publication and other rights in association with the copyright in the Thesis, and except as herein before provided, neither the Thesis nor any substantial portion thereof may be printed or otherwise reproduced in any material form whatsoever without the author’s prior written permission. date Emmanuel Cabral Master of Science xii This work is dedicated to my parents. For showing me the beauty of science. xiv Acknowledgements “When I gave lectures on thermodynamics to an undergraduate chemistry audience I often began by saying that no other scientific law has contributed more to the liberation of the human spirit than the second law of thermodynamics”. – Dr. Peter Atkins (Atkins, 2007). I would like to start by offering my most sincere gratitude to my supervisor, Dr. Páll Valdimarsson, who from the very first interaction we had expressed a remarkable trust on the thesis and on me and had a better idea of what the research was going to look like than I did. Similarly, I offer my deepest gratitude to my advisor Dr. William Scott Harvey, for being a guiding voice throughout the research, for putting his time and interest into this project, and giving both his friendly and a professional insight on all aspects of the thesis. To both of you, thanks for all the laughs, criticism, and advises, they will forever guide me in my professional life. Special thanks to L‘Eurométropole de Strasbourg for providing all the necessary resources, connections, and facilities during the research period in France. My deepest acknowledgements as well to all the professionals (especially all of you in the department of Direction de Mission Energie) that played a significant role throughout different meetings to assess the different industrial proposals, applications, and energy demand scenarios. The research was conducted as part of a collaboration between the MSc. Sustainable Energy Engineering programme of the Iceland School of Energy in Reykjavik University, and the Energy and Climatic Engineering programme of National Institute of Applied Sciences of Strasbourg (INSA-Strasbourg). Acknowledgements to Fonroche Géothermie and Electricité de Strasbourg for the roles they played in the development of all current geothermal projects in Alsace, and special thanks for attending some of the presentations done during the research period in France, as well as all their insights and recommendations throughout the research. This work was partially founded by the Eurométropole de Strasbourg, and Háskólinn í Reykjavík through the Erasmus+ exchange programme. xvi Preface This following research is original work by the author, Emmanuel Cabral. The research was conducted as part of a master’s thesis, required for the internship conducted at the Départament de Mission Energie of the Eurométropole de Strasbourg, and an exchange between the MSc. Sustainable Energy Engineering programme in Reykjavík University, and the Génie Climatique et Energétique programme of INSA-Strasbourg. The research was conducted during a seven-month period in Strasbourg, Alsace, and most of the assumptions and information found throughout the research was gathered during the period of internship. The concluding remarks in the research were conducted while in Reykjavík, after the internship period had ended, and the data and document were successfully revised and verified. The last part of the research focuses on a thermoeconomic (exergoeconomic) analysis of the selected utilization scenario for the Vendenheim geothermal resource. A special notice must be made at this point for all calculations are based on the assumptions made throughout the research, as well as data used from literature review which is respectively mentioned in this research. Although the proyect uses data from the real proyects currently being conducted in Vendenheim, it is by no means a numerical modelling of the geothermal binary plant that will be built in the mentioned location. The mathematical model and numerical model were built to help address the utilization of the geothermal resource and may serve as a reference for future research in the implementation of a similar, or a more advanced binary system and/or cascading applications. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without prior permission of the author, Reykjavík University, or L‘Eurométropole de Strasbourg. xviii xix Contents Acknowledgements ........................................................................................................... xv Preface .............................................................................................................................. xvii Contents ............................................................................................................................ xix List of Figures .................................................................................................................. xxii List of Tables .................................................................................................................
Load more

Recommended publications
  • The Jewish Presence in Soufflenheim
    THE JEWISH PRESENCE IN SOUFFLENHEIM By Robert Wideen : 2018 Soufflenheim Genealogy Research and History www.soufflenheimgenealogy.com Jews are first mentioned in Alsace in the 12th century. There were 522 families in 1689 and 3,910 families in 1784, including four families totaling 19 people in Soufflenheim. By 1790, the Jewish population in Alsace had grown to approximately 22,500, about 3% of the population. They maintained their own customs, spoke Yiddish, and followed Talmudic laws enforced by their Rabbis. There was a Jewish presence in Soufflenheim since the 15th century, and probably earlier. By the late 1700’s there was a Jewish street in the village, a Jewish lane on the outskirts, a district known as Juden Weeg, and a Jewish path in the Judenweg area of the Haguenau Forest leading to the Jewish Forest Road. Their influence on the local dialect is documented in Yiddish in the Speech of Soufflenheim. Jewish Communities of Alsace, Including those of the Middle Ages. Encyclopaedia Judaica (1971) CONTENTS The Jewish Presence in Soufflenheim .......................................................................................................... 1 Soufflenheim Jews ........................................................................................................................................ 3 Their History .................................................................................................................................................. 5 The Earliest Jews .....................................................................................................................................
    [Show full text]
  • Let Yourself Be Guided…
    Let yourself be guided… tourism-alsace.com Contents Introduction 4 to 7 Strasbourg Colmar and Mulhouse Escape into a natural paradise 8 to 17 Discover nature Parks and gardens Well-being and health resorts Wildlife parks and theme parks Hiking Cycle touring, mountain biking, high wire adventure parks, climbing Horseback packing Golf and mini-golf courses Waterborne tourism Water sports, swimming Airborne sports Fishing Winter sports Multi-activity holidays Taste unique local specialities! 18 to 25 Gastronomy, wine seminar, cookery classes Visit the markets Museums of arts and traditions Towns and villages “in bloom”, handicraft Half-timbered houses, traditional Alsatian costume Festivals and traditions Lay siege to history! 26 to 35 Museums Land of fortified castles Memorial sites Religious heritage Practical information about Alsace 36 to 45 Access Accommodation Disabled access Alsace without the car Family holidays in Alsace Weekend and mini-breaks French lessons Festivals, shows and events Tourist Information Offices Tourist trails and routes Map of Alsace The guide to your stay in Alsace Nestling between the Vosges and the Rhine, Alsace is a charming little region with a big reputation. At the crossroads of the Germanic and Latin worlds, it is passionate about its History, yet firmly anchored in modern Europe and open to the world. Rated as among the most beautiful in France, the Alsatian towns and cities win the “Grand prix national de fleurissement”, “Towns in Bloom” prices every year. Through their festivals and their traditions, they have managed to preserve a strong identity based on a particular way of living. World famous cuisine, a remarkably rich history, welcoming and friendly people: in this jewel of a region there really is something for everyone.
    [Show full text]
  • Group Directory 2021
    Group Directory 2021 2 Eurofins: Network of laboratories Each laboratory offers analytical services and customer support, however, some services are centralised. Through excellent logistics and information technology, Eurofins can deliver a full range of expertise through any one of its laboratories. In this directory, services listed are specific to the respective laboratories and are described as follows: o International Division/ International Business Line o Country (by alphabetical order) o Laboratory - Marketing name o Laboratory description/ Services/ Analysis/ Offers o Full contact information: o Legal name of the laboratory . Full address and phone number(s) . Email(s) . Website Food & Feed Testing ........................................................... 7 Italy .................................................................... 49 Australia .............................................................. 7 Spain ................................................................. 49 Austria ................................................................. 7 USA ................................................................... 49 Belgium ............................................................... 7 Sensory & Marketing Research .......................................... 51 Brazil.................................................................... 7 China ................................................................. 51 Bulgaria ............................................................... 8 France ..............................................................
    [Show full text]
  • Zones PTZ 2017
    Zones PTZ 2017 - Maisons Babeau Seguin Pour construire votre maison au meilleur prix, rendez-vous sur le site de Constructeur Maison Babeau Seguin Attention, le PTZ ne sera plus disponible en zone C dès la fin 2017 et la fin 2018 pour la zone B2 Région Liste Communes N° ZONE PTZ Département Commune Région Département 2017 67 Bas-Rhin Adamswiller Alsace C 67 Bas-Rhin Albé Alsace C 67 Bas-Rhin Allenwiller Alsace C 67 Bas-Rhin Alteckendorf Alsace C 67 Bas-Rhin Altenheim Alsace C 67 Bas-Rhin Altwiller Alsace C 67 Bas-Rhin Andlau Alsace C 67 Bas-Rhin Artolsheim Alsace C 67 Bas-Rhin Aschbach Alsace C 67 Bas-Rhin Asswiller Alsace C 67 Bas-Rhin Auenheim Alsace C 67 Bas-Rhin Baerendorf Alsace C 67 Bas-Rhin Balbronn Alsace C 67 Bas-Rhin Barembach Alsace C 67 Bas-Rhin Bassemberg Alsace C 67 Bas-Rhin Batzendorf Alsace C 67 Bas-Rhin Beinheim Alsace C 67 Bas-Rhin Bellefosse Alsace C 67 Bas-Rhin Belmont Alsace C 67 Bas-Rhin Berg Alsace C 67 Bas-Rhin Bergbieten Alsace C 67 Bas-Rhin Bernardvillé Alsace C 67 Bas-Rhin Berstett Alsace C 67 Bas-Rhin Berstheim Alsace C 67 Bas-Rhin Betschdorf Alsace C 67 Bas-Rhin Bettwiller Alsace C 67 Bas-Rhin Biblisheim Alsace C 67 Bas-Rhin Bietlenheim Alsace C 67 Bas-Rhin Bindernheim Alsace C 67 Bas-Rhin Birkenwald Alsace C 67 Bas-Rhin Bischholtz Alsace C 67 Bas-Rhin Bissert Alsace C 67 Bas-Rhin Bitschhoffen Alsace C 67 Bas-Rhin Blancherupt Alsace C 67 Bas-Rhin Blienschwiller Alsace C 67 Bas-Rhin Boesenbiesen Alsace C 67 Bas-Rhin Bolsenheim Alsace C 67 Bas-Rhin Boofzheim Alsace C 67 Bas-Rhin Bootzheim Alsace C 67 Bas-Rhin
    [Show full text]
  • (M Supplément) Administration Générale Et Économie 1800-1870
    Archives départementales du Bas-Rhin Répertoire numérique de la sous-série 15 M (M supplément) Administration générale et économie 1800-1870 Dressé en 1980 par Louis Martin Documentaliste aux Archives du Bas-Rhin Remis en forme en 2016 par Dominique Fassel sous la direction d’Adélaïde Zeyer, conservateur du patrimoine Mise à jour du 19 décembre 2019 Sous-série 15 M – Administration générale et économie, 1800-1870 (M complément) Page 2 sur 204 Sous-série 15 M – Administration générale et économie, 1800-1870 (M complément) XV. ADMINISTRATION GENERALE ET ECONOMIE COMPLEMENT Sommaire Introduction Répertoire de la sous-série 15 M Personnel administratif ........................................................................... 15 M 1-7 Elections ................................................................................................... 15 M 8-21 Police générale et administrative............................................................ 15 M 22-212 Distinctions honorifiques ........................................................................ 15 M 213 Hygiène et santé publique ....................................................................... 15 M 214-300 Divisions administratives et territoriales ............................................... 15 M 301-372 Population ................................................................................................ 15 M 373 Etat civil ................................................................................................... 15 M 374-377 Subsistances ............................................................................................
    [Show full text]
  • Février 2021 Télécharger
    Numéro 40 février 2021 le vil s la dan illage Un v LABEL 2010 - 2013 2014 - 2017 & 03 88 56 20 00 - www.niederhausbergen.fr - [email protected] Edito rial LA VIE COMMUNALE Mesdames, Messieurs, chers concitoyens, DES NOUVEAUTES DÈS CETTE ANNÉE ET LA PRÉPARATION DE L’AVENIR Cela fait une année déjà que nous avons tous été happés par D’ores et déjà, nous mettons en œuvre : le tourbillon de la COVID-19 et ses conséquences sur notre vie l La rénovation de l’éclairage public des quartiers Est de tous les jours. courant février et du quartier du Hameau en automne 2021 l Le lotissement communal Langenthal au second C’était impensable jusqu’alors et pourtant les faits nous ont trimestre de cette année donné tort. La résilience de l’humanité a toujours été d’oublier l Le lancement des études techniques pour la rénovation les moments tragiques en se persuadant que cela n’arriverait de la mairie, la construction d’un dépôt municipal, l’adaptation du plus jamais, car nos sociétés ont toujours eu la capacité de trouver groupe scolaire et du périscolaire au développement démo les solutions et d’éradiquer les maux sanitaires définitivement. graphique de la commune et aux crises sanitaires potentielles, et le démarrage des études pour la réalisation d’une bibliothèque Ce virus et l’ampleur de ses conséquences nous ont remis les dans un bâtiment dédié idées -souvent préconçues- en place, et nous rappellent sévèrement l Un parcours santé sur la colline pour l’automne qu’il n’en est rien et que rien n’est jamais définitif ! l Une réflexion pour la réalisation de jardins partagés opérationnels en 2022 Regardez par ailleurs, l’actualité quotidienne et sa cohorte de l La création d’espaces arborés et ombragés drames permanents économiques, démocratiques, religieux, écologiques.
    [Show full text]
  • Hume, Sara. "Between Fashion and Folk: Dress Practices in Alsace During the First World War." Fashion, Society, and the First World War: International Perspectives
    Hume, Sara. "Between fashion and folk: Dress practices in Alsace during the First World War." Fashion, Society, and the First World War: International Perspectives. Ed. Maude Bass-Krueger, Hayley Edwards-Dujardin and Sophie Kurkdjian. London: Bloomsbury Visual Arts, 2021. 108–121. Bloomsbury Collections. Web. 2 Oct. 2021. <http:// dx.doi.org/10.5040/9781350119895.ch-007>. Downloaded from Bloomsbury Collections, www.bloomsburycollections.com, 2 October 2021, 00:13 UTC. Copyright © Selection, editorial matter, Introduction Maude Bass-Krueger, Hayley Edwards- Dujardin, and Sophie Kurkdjian and Individual chapters their Authors 2021. You may share this work for non-commercial purposes only, provided you give attribution to the copyright holder and the publisher, and provide a link to the Creative Commons licence. 7 Between fashion and folk Dress practices in Alsace during the First World War S a r a H u m e On November 22, 1918, the triumphant French forces entered Alsace following the German defeat. Th e victorious troops parading through the streets of Strasbourg were met with expressions of delirious joy from Alsatians. Th e festivities were documented in motion pictures, still photographs, postcards, posters, and countless illustrations (Figure 7.1). Th e girls, wearing enormous black bows, greeting the entering soldiers came to be the defi ning image of the day. Th e traditional costume of Alsace served as a symbol of the region, and in this enactment of Alsace’s return to French control, the Alsatians received the French as their liberators. Th e link in the popular imagination between the Alsatian traditional costume and loyalty to France deserves further consideration.
    [Show full text]
  • T3 À Vendre Berstett Immobilière
    BERSTETT - Beau 3P bien Equipé, au Dernier Etage ! 200 450 € 65 m² 3 pièces Berstett Type d'appartement T3 Surface 65.00 m² Séjour 24 m² Pièces 3 Chambres 2 Salle d'eau 1 avec Fenêtre et meuble WC 1 Étage 2 Epoque, année 2004 Ancien État général En bon état Gaz Chauffage Individuel Aménagée et équipée, Coin Cuisine cuisine Ameublement Partiellement meublé Vue Cour Ouvertures PVC, Double vitrage Exposition Sud-Est Stationnement int. 1 Garage au RDCH ext. Stationnement ext. 1 Place privative Ascenseur Non Cave Non Taxe foncière 409 €/an Charges 80 € /mois Référence VA2086, Mandat N°4278 A DECOUVRIR sur BERSTETT - KOCHERSBERG - ***Nouvelle EXCLUSIVITE :-) *** A proximité immédiate de Vendenheim et de Truchtersheim, nous vous proposons dans un Environnement très peu passant, ce Beau 3P de 72.84m² au sol, 65,72m² carrez, et 69m² de surface pondérée, Fonctionnel et Complet, en Dernier étage d’une Copropriété bien tenue ! Au 2e Etage de la Résidence SANS Ascenseur, l’Appartement s’articule ainsi : 1 coin Entrée 1 Salon-Séjour de 24m², s’ouvrant sur un très beau balcon aménagé, et jouxtant un grand coin Cuisine de 10m², elle-même parfaitement équipée (lave- vaisselle, plaque de cuisson, hotte, réfrigérateur, four) et aménagée (mobilier à profusion) ! 1 Couloir/Dégagement avec placard mural 2 Chambres (11m² + 12m²) 1 WC indépendant 1 Salle d’eau non aveugle avec meuble vasque et douche de 4m² A l’EXTERIEUR au RDCH : 1 Garage avec coin rangement 1 Place de parking privative LES CHIFFRES et AUTRES : Chauffage et production d’eau chaude au Gaz (actuellement 67Eur/mois pour un couple) Ensemble Immobilier de 2003/2004 composé de 2 bâtiments - soumis aux statuts de la Copropriété - 16 lots principaux sur 62 au total - Budget moyen annuel de la quote-part de charges courantes : 970Euros soit 80Eur/mois Procédure en cours : Non Taxe Foncières : 409 Euros Quelques informations transports : Strasbourg à 20min, Truchtersheim à 7min, Ligne de Bus 210 Mandat N° 4278.
    [Show full text]
  • Hoerdt Kilstett Strasbourg
    Vers A.35 Vers SELTZ Vers A.35 Vers STRASBOURG Vers KILSTETT HOERDT KILSTETT Vers HOERDT LA WANTZENAU Vers REICHSTETT / BISCHHEIM HONAU Vers STRASBOURG STRASBOURG COMMUNAUTE URBAINE DE STRASBOURG SERVICE DE L'INFORMATION GEOGRAPHIQUE LEUTESHEIM www.sig-strasbourg.net LA WANTZENAU DATE D'EDITION : Novembre 2008 REPRODUCTION INTERDITE Service Information Géographique 100 0 100 200 300 400 500m ECHELLE: 50 Limite de commune Ligne de chemin de fer Point de niveau Axe de circulation Bâtiment public Surface bâtie F o r ê t C i m e t i è r e Cimetière israélite REPERTOIRE DES RUES - BATIMENTS ET AMENAGEMENTS PUBLICS DE LA WANTZENAU ***************** Epinoche (rue de l') E-F-5 Mirabelles (impasse des) D-6 *************************** Erable (rue de l') E-5 Moissons (rue des) C-5-6 BATIMENTS ET LA WANTZENAU Etang (rue de l') E-5-6 Monnet (cours Jean) B-2 AMENAGEMENTS PUBLICS ***************** Europe (place de l') B-1 Morilles (rue des) E-F-5 *************************** 19 Mars 1962 (place du) E-6 Faisan (rue du) F-5-6 Moulin (impasse du) B-7 ATELIERS MUNICIPAUX D-5 Acacia (rue de l') E-5 Forêt (rue de la) E-F-5 Moulin (rue du) C-D-6 CASERNE DE GENDARMERIE D-E-4 Acker (rue du Maire Léon) C-D-5-6 Fossé (rue du) D-4 Myosotis (impasse des) D-4 CASERNE DE POMPIERS D-4 Albert Calmette (rue) A-B-3-4 Frêne (rue du) E-4-5 Neumatt (rue) C-D-3-4 CIMETIERE C-D-4 Albert Zimmer (rue) C-D-5 Gare (rue de la) D-4-5 Neuve (rue) D-4-5 CIMETIERE D-E-3-4 Alençon (faubourg du Capitaine d') D-6-7 Général de Gaulle (rue du) C-D-5 Nord (rue du) D-4 CLUB HIPPIQUE LE WALDHOF
    [Show full text]
  • Pièce 1E Étude D'impact
    DAU–GMING–30230–PIÈCE 1E : ÉTUDE D’IMPACT PIÈCE 1E ÉTUDE D’IMPACT 3/4 REVISION DU DOCUMENT Concessionnaire Indice du document Pages modifiées et / ou ajoutées CONTOURNEMENT OUEST DE STRASBOURG TITRE 1 CONCEPTION / DAU / ETUDE D’IMPACT ENSEMBLE DU PROJET DOSSIER D’AUTORISATION UNIQUE Etabli par : VOLET 1 : EAUX ET MILIEUX AQUATIQUES Quadrigramme : Cécile Cren PIECE 1 E : ETUDE D’IMPACT 2006 Vérifié par : Quadrigramme : Pauline Jaulin Concepteur-Constructeur Sous-Groupement Partenaire / Sous-Traitant / Prestataire Validé par : N/A N/A Quadrigramme : Philippe Ravache I B0 2017-01 CCRE PJAU PRAV Etabli Vérifié Validé INDICE DATE MODIFICATION par par par Commentaire et document de référence Format : A3 Echelle : N/A Pages 1/180 C ENV ENS 000 00000 DAU GMING 30225 B0 Phase Métier Zone Item PK Type Doc. Emetteur N° Chrono ou N° de Série Indice Pièce E : Etude d’impact Pièce E : Etude d’impact SOMMAIRE E3.1.3 Milieu humain ........................................................................................ 50 E3.2 impacts du programme ...................................................................... 53 E3.2.1Effets localisés........................................................................................ 53 E0. Index des communes citées..................................................... 8 E3.2.2 Effets cumulés du programme ............................................................... 54 E1. Résumé non technique............................................................. 9 E3.2.3 Impact sur les circulations ...................................................................
    [Show full text]
  • Truchtersheim Saessolsheim Saverne
    www.bas-rhin.fr LIGNE Truchtersheim Saessolsheim Saverne 405 [email protected] - Tél : 03 88 76 67 67 67 76 88 03 : Tél - [email protected] 67 964 Strasbourg Cedex 9 Cedex Strasbourg 964 67 Place du Quartier Blanc Quartier du Place JOUR DE CIRCULATION LMMeJV LMMeJV LMMeJV LMMeJV LMMeJV LMMeJV LMMeJV LMMeJV LMMeJV LMMeJV S S S S S : Bas-Rhin du général Conseil du Coordonnées Calendrier 2012 Circule en période scolaire • • • • • • • • • • • Circule en période de petites vacances • • • • • • • Juil. Août Sept. Oct. Nov. Déc. Renvois à consulter Corresopndance ligne 220 08:18 09:11 13:21 17:05 18:05 18:35 09:09 11:59 13:21 17:01 D 1 Me 1 S 1 L 1 J 1 S 1 en provenance de Strasbourg L 2 J 2 D 2 M 2 V 2 D 2 TRUCHTERSHEIM Collège du Kochersberg (1) 06:20 06:45 06:45 08:22 09:15 13:27 17:10 18:15 18:45 06:45 09:15 12:25 13:27 17:10 M 3 V 3 L 3 Me 3 S 3 L 3 Ancienne gare 06:21 06:46 06:46 08:23 09:16 13:28 17:11 18:16 18:46 06:46 09:16 12:26 13:28 17:11 Me 4 S 4 M 4 J 4 D 4 M 4 Place du Marché 06:22 06:47 06:47 08:24 09:17 13:29 17:12 18:17 18:47 06:47 09:17 12:27 13:29 17:12 J 5 D 5 Me 5 V 5 L 5 Me 5 Château d'eau 06:23 06:48 06:48 08:25 09:18 13:30 17:13 18:18 18:48 06:48 09:18 12:28 13:30 17:13 Strasbourg - Halles des routière Gare REITWILLER Mairie 06:24 06:49 06:49 08:26 09:19 13:31 17:14 18:19 18:49 06:49 09:19 12:29 13:31 17:14 V 6 L 6 J 6 S 6 M 6 J 6 GIMBRETT Centre 06:28 06:53 06:53 08:30 09:23 13:35 17:18 18:23 18:53 06:53 09:23 12:33 13:35 17:18 S 7 M 7 V 7 D 7 Me 7 V 7 GOUGENHEIM Route de Mittelhausen 06:32 06:57 06:57 08:34 09:27 13:39 17:22 18:27 18:57 06:57 09:27 12:37 13:39 17:22 D 8 Me 8 S 8 L 8 J 8 S 8 : par exploitée est ligne Cette Place de la Libération 06:33 06:58 06:58 08:35 09:28 13:40 17:23 18:28 18:58 06:58 09:28 12:38 13:40 17:23 L 9 J 9 D 9 M 9 V 9 D 9 ROHR Place de l'Eglise 06:37 07:02 07:02 08:39 09:32 13:44 17:27 18:32 19:02 07:02 09:32 12:42 13:44 17:27 M 10 V 10 L 10 Me 10 S 10 L 10 Lot.
    [Show full text]
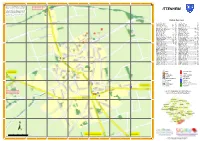
  • ITTENHEIM Commons)
    A B C D E F G Sources : d'après BD TOPO IGN 2020, BD ORTHO IGN 2015 ; Plan cadastral DGI 2020 ; Voirie réactua- lisée avec la participation des communes en 2021. Ce plan est produit et édité sous licence CC (Créative ITTENHEIM Commons). Réutilisation et reproduction à but non lu- cratif autorisée sous réserve de citation des sources. 1 Communauté de communes du Kochersberg et de 1 l'Ackerland - Fév. 2021 Index des rues Abeilles (Rue des) ............................. D5 Iris (Rue des) ..................................... D3 Acacias (Rue des) ..................... C2 - B2 Jardins (Rue des) ............................... C5 Achenheim (Route d') ................ E5 - G7 Lavoir (Place du) ............................... D4 Albert Schweitzer (Rue) ............. D4 - D5 Licorne (Impasse de la) ..................... D4 Asperges (Rue des) ........................... E3 Lilas (Rue des) ........................... D4 - E3 Asteroïde B612 (Sentier de l') ..... D2 - E2 Louis Pasteur (Rue) .................... C3 - E5 Baobab (Sentier du) ........................... E2 Luberon (Rue du) .............................. C4 Bleuets (Rue des) .............................. D4 Lupuline (Rue de la) ................... D4 - C4 2 2 Bois (Chemin du) ......................... E2 - G1 Magnolias (Place des) ......................... D3 Bonnieux (Rue de) ...................... C5 - C4 Mairie (Rue de la) .............................. E4 Bosquets (Rue des) ..................... C1 - B1 Molsheim (Chemin de) ................ E5 - C7 Breuschwickersheim (Route de) .
    [Show full text]