DOCSLIB.ORG

Primitive Lattice Vectors

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Primitive Lattice Vectors Primitive lattice vectors Q: How can we describe these lattice vectors (there are an infinite number of them)? A: Using primitive lattice vectors (there are only d of them in a d-dimensional space). For a 3D lattice, we can find three primitive lattice vectors (primitive translation vectors), such that any translation vector can be written as �⃗ = �%�⃗% + �(�⃗( + �)�⃗) where �%, �( and �) are three integers. For a 2D lattice, we can find two primitive lattice vectors (primitive translation vectors), such that any translation vector can be written as �⃗ = �%�⃗% + �(�⃗( where �% and �( are two integers. For a 1D lattice, we can find one primitive lattice vector (primitive translation vector), such that any translation vector can be written as �⃗ = �%�⃗% where �% is an integer. Primitive lattice vectors Red (shorter) vectors: �⃗% and �⃗( Blue (longer) vectors: �% and �( �⃗% and �⃗( are primitive lattice vectors �% and �( are NOT primitive lattice vectors 1 �% = 2�⃗% + 0 �⃗( �⃗ = � + 0� % 2 % ( Integer coefficients noninteger coefficients Primitive lattice vectors The choices of primitive lattice vectors are NOT unique. Primitive cell in 2D The parallelogram defined by two primitive lattice vectors form a primitive cell. Ø the Area of a primitive cell: A = |�⃗%× �⃗(| Ø Each primitive cell contains 1 site. Primitive cell in 3D The parallelepiped defined by the three primitive lattice vectors are called a primitive cell. A special case: a cuboid Ø the volume of a primitive cell: V = |�⃗%. (�⃗(× �⃗))| Ø each primitive cell contains 1 site. Wigner–Seitz cell Ø the volume of a Wigner-Seitz cell is the same as a primitive cell Ø each Wigner-Seitz cell contains 1 site (same as a primitive cell). Rotational symmetries Rotational symmetries: If a system goes back to itself when we rotate it along certain axes by some angle �, we say that this system has a rotational symmetry. Ø For the smallest �, 2�/� is an integer, which we will call �. Ø We say that the system has a �-fold rotational symmetry along this axis. For Bravais lattices, Ø It can be proved that � can only take the following values: 1, 2, 3, 4 or 6. Mirror planes Mirror Planes: 2D Bravais lattices http://en.wikipedia.org/wiki/Bravais_lattice 3D Bravais lattices http://en.wikipedia.org/wiki/Bravais_lattice Cubic system Conventional cells Ø For a simple cubic lattice, a conventional cell = a primitive cell Ø NOT true for body-centered or face-centered cubic lattices How can we see it? Ø sc: one conventional cell has one site (same as a primitive cell) Ø bcc: one conventional cell has two sites (twice as large as a primitive cell) Ø fcc: one conventional cell has four cites (1 conventional cell=4 primitive cells) Simple cubic Lattice sites: �(� �? + � �?+ n �̂) % Lattice point per conventional cell: 1 = 8× E Volume (conventional cell): �) Volume (primitive cell) : �) Number of nearest neighbors: 6 Nearest neighbor distance: � Number of second neighbors: 12 Second neighbor distance: F 2� G Packing fraction: ≈ 0.524 H Coordinates of the sites: (�, �, �) For the site 0,0,0 , 6 nearest neighbors: ±1,0,0 , 0, ±1,0 and 0,0, ±1 12 nest nearest neighbors: ±1, ±1,0 , 0, ±1, ±1 and (±1,0, ±1) Packing fraction Packing fraction: We try to pack N spheres (hard, cannot deform). MN The total volume of the spheres is �4 � ) MN The volume these spheres occupy V > �4 � (there are spacing) ) Packing fraction=total volume of the spheres/total volume these spheres occupy �) �) �) �4 � 4 � 4 � ������� �������� = 3 = 3 = 3 � �/� ������ ��� ���� �) 4 � = 3 ������ �� � ��������� ���� High packing fraction means the space is used more efficiently Simple cubic Lattice sites: �(� �? + � �?+ n �̂) % Lattice point per conventional cell: 1 = 8× E Volume (conventional cell): �) Volume (primitive cell) : �) Number of nearest neighbors: 6 Nearest neighbor distance: � Number of second neighbors: 12 Second neighbor distance: F 2� G Packing fraction: ≈ 0.524 H �) 4 � ������� �������� = 3 Nearest distance= 2 R ������ �� � ��������� ���� R= Nearest distance/2=�/2 �) 4 � 4 � � 4 � �/2 � = 3 = ( ))= ( ))= ≈ 0.524 �) 3 � 3 � 6 Ø About half (0.524=52.4%) of the space is really used by the sphere. Ø The other half (0.476=47.6%) is empty. bcc Lattice sites % % % �(� �? + � �?+ n �̂) and �[ � + �? + � + �? + � + �̂] ( ( ( % Lattice point per conventional cell: 2 = 8× + 1 E Volume (conventional cell): �) Volume (primitive cell) : �)/2 Number of nearest neighbors: 8 F F a a a ) Nearest neighbor distance: ( )(+( )(+( )(= � ≈ 0.866� ( ( ( ( Number of second neighbors: 6 Second neighbor distance: � F ) Packing fraction: � ≈ 0.680 E Coordinates of the sites: (�, �, �) For the site 0,0,0 , % % % 8 nearest neighbors: ± , ± , ± ( ( ( 6 nest nearest neighbors: ±1,0,0 , 0, ±1,0 and (0,0, ±1) bcc packing fraction Volume (primitive cell) : �)/2 F F a a a ) Nearest neighbor distance: ( )(+( )(+( )(= � ≈ 0.866� ( ( ( ( F ) Packing fraction: � ≈ 0.680 E �) Nearest distance= 2 R 4 � 3 F ) ������� �������� = R= Nearest distance/2= � ������ �� � ��������� ���� b �) F 3 4 � 8� � 8� � F 3� = 3 = ( ))= ( 4 ))= ≈ 0.680 �)/2 3 � 3 � 8 Ø About 68.0% of the space is really used by the sphere. Ø About 32.0% of the space is empty. fcc Lattice sites % % �(� �? + � �?+ n �̂) �[ � + �? + � + �? + � �̂] ( ( % % �[ � + �? + � �? + � + �̂] ( ( % % �[��? + � + �? + � + �̂] ( ( % % Lattice point per conventional cell: 4 = 8× + 6× = 1 + 3 E ( Volume (conventional cell): �) Volume (primitive cell) : �)/4 Number of nearest neighbors: 12 F F a a ( Nearest neighbor distance: ( )(+( )(+(0)(= � ≈ 0.707� ( ( ( Number of second neighbors: 6 Second neighbor distance: � For the site 0,0,0 , % % % % % % 12 nearest neighbors: ± , ± , 0 , ± , 0, ± and 0, ± , ± ( ( ( ( ( ( 6 nest nearest neighbors: ±1,0,0 , 0, ±1,0 and (0,0, ±1) fcc packing fraction Volume (primitive cell) : �)/4 F F a a ( Nearest neighbor distance: ( )(+( )(+(0)(= � ≈ 0.707� ( ( ( �) Nearest distance= 2 R 4 � 3 F ( ������� �������� = R= Nearest distance/2= � ������ �� � ��������� ���� b �) F 2 4 � 16� � 16� � F 2� = 3 = ( ))= ( 4 ))= ≈ 0.740 �)/4 3 � 3 � 6 Ø About 74.0% of the space is really used by the sphere. Ø About 26.0% of the space is empty. 0.740 is the highest packing fraction one can ever reach. This structure is called “close packing” There are other close packing structures (same packing fraction) Cubic system hexagonal 2D planes formed by equilateral triangles Stack these planes on top of each other Primitive cell: a right prism based on a rhombus with an included angle of 120 degree. Volume (primitive cell): ��� = ����×ℎ���ℎ� 1 F 3 F 3 = 2 × �( � = �(� 2 2 % ) 2 Hexagonal Close-Packed Structure (hcp) Ø Let’s start from 2D (packing disks, instead of spheres). Q: What is the close-pack structure in 2D? A: The hexagonal lattice (these disks form equilateral triangles) Ø Now 3D: Q: How to get 3D close packing? A: Stack 2D close packing structures on top of each other. Hexagonal Close-Packed Structure (hcp) hcp: ABABAB… fcc: ABCABCABC… Atoms inside a unit cell Ø We choose three lattice vectors Ø Three lattice vectors form a primitive or a conventional unit cell Ø Length of these vectors are called: the lattice constants We can mark any unit cell by three integers: ��� �⃗ = ��⃗% + � �⃗( + � �⃗) Coordinates of an atom: We can mark any atom in a unit cell by three real numbers: ���. The location of this atom: � �⃗% + � �⃗( + � �⃗) Notice that 0 ≤ � < 1 and 0 ≤ � < 1 and 0 ≤ � < 1 Q: Why x cannot be 1? A: Due to the periodic structure. 1 is just 0 in the next unit cell Sodium Chloride structure Sodium Chloride structure Face-centered cubic lattice Na+ ions form a face-centered cubic lattice Cl- ions are located between each two neighboring Na+ ions Equivalently, we can say that Cl- ions form a face-centered cubic lattice Na+ ions are located between each two neighboring Na+ ions Sodium Chloride structure Primitive cells Cesium Chloride structure Cesium chloride structure Simple cubic lattice Cs+ ions form a cubic lattice Cl- ions are located at the center of each cube Equivalently, we can say that Cl- ions form a cubic lattice Cs+ ions are located at the center of each cube Coordinates: Cs: 000 % % % Cl: ( ( ( Notice that this is a simple cubic lattice NOT a body centered cubic lattice Ø For a bcc lattice, the center site is the same as the corner sites Ø Here, center sites and corner sites are different Diamond structure Carbon atoms can form 4 different crystals Graphene (Nobel Prize carbon) Nano tubes Diamond (money carbon/love carbon) Graphite (Pencil carbon) Not all lattices are Bravais lattices: examples the honeycomb lattice (graphene) Diamond lattice is NOT a Bravais Lattice either Same story as in graphene: We can distinguish two different type of carbon sites (marked by different color) We need to combine two carbon sites (one black and one white) together as a (primitive) unit cell If we only look at the black (or white) sites, we found the Bravais lattice: fcc Cubic Zinc Sulfide Structure Very similar to Diamond lattice Now, black and white sites are two different atoms fcc with two atoms in each primitive cell Good choices for junctions Diode Matter Matter gas/liquid: solids: Atoms/molecules Atoms/molecules can move around cannot move Crystals: Random solids: Atoms/molecules Atoms/molecules form a periodic form a random structure structure.
Load more

Recommended publications
  • Crystal Structure of a Material Is Way in Which Atoms, Ions, Molecules Are Spatially Arranged in 3-D Space
    Crystalline Structures – The Basics •Crystal structure of a material is way in which atoms, ions, molecules are spatially arranged in 3-D space. •Crystal structure = lattice (unit cell geometry) + basis (atom, ion, or molecule positions placed on lattice points within the unit cell). •A lattice is used in context when describing crystalline structures, means a 3-D array of points in space. Every lattice point must have identical surroundings. •Unit cell: smallest repetitive volume •Each crystal structure is built by stacking which contains the complete lattice unit cells and placing objects (motifs, pattern of a crystal. A unit cell is chosen basis) on the lattice points: to represent the highest level of geometric symmetry of the crystal structure. It’s the basic structural unit or building block of crystal structure. 7 crystal systems in 3-D 14 crystal lattices in 3-D a, b, and c are the lattice constants 1 a, b, g are the interaxial angles Metallic Crystal Structures (the simplest) •Recall, that a) coulombic attraction between delocalized valence electrons and positively charged cores is isotropic (non-directional), b) typically, only one element is present, so all atomic radii are the same, c) nearest neighbor distances tend to be small, and d) electron cloud shields cores from each other. •For these reasons, metallic bonding leads to close packed, dense crystal structures that maximize space filling and coordination number (number of nearest neighbors). •Most elemental metals crystallize in the FCC (face-centered cubic), BCC (body-centered cubic, or HCP (hexagonal close packed) structures: Room temperature crystal structure Crystal structure just before it melts 2 Recall: Simple Cubic (SC) Structure • Rare due to low packing density (only a-Po has this structure) • Close-packed directions are cube edges.
    [Show full text]
  • Types of Lattices
    Types of Lattices Types of Lattices Lattices are either: 1. Primitive (or Simple): one lattice point per unit cell. 2. Non-primitive, (or Multiple) e.g. double, triple, etc.: more than one lattice point per unit cell. Double r2 cell r1 r2 Triple r1 cell r2 r1 Primitive cell N + e 4 Ne = number of lattice points on cell edges (shared by 4 cells) •When repeated by successive translations e =edge reproduce periodic pattern. •Multiple cells are usually selected to make obvious the higher symmetry (usually rotational symmetry) that is possessed by the 1 lattice, which may not be immediately evident from primitive cell. Lattice Points- Review 2 Arrangement of Lattice Points 3 Arrangement of Lattice Points (continued) •These are known as the basis vectors, which we will come back to. •These are not translation vectors (R) since they have non- integer values. The complexity of the system depends upon the symmetry requirements (is it lost or maintained?) by applying the symmetry operations (rotation, reflection, inversion and translation). 4 The Five 2-D Bravais Lattices •From the previous definitions of the four 2-D and seven 3-D crystal systems, we know that there are four and seven primitive unit cells (with 1 lattice point/unit cell), respectively. •We can then ask: can we add additional lattice points to the primitive lattices (or nets), in such a way that we still have a lattice (net) belonging to the same crystal system (with symmetry requirements)? •First illustrate this for 2-D nets, where we know that the surroundings of each lattice point must be identical.
    [Show full text]
  • The Metrical Matrix in Teaching Mineralogy G. V
    THE METRICAL MATRIX IN TEACHING MINERALOGY G. V. GIBBS Department of Geological Sciences & Department of Materials Science and Engineering Virginia Polytechnic Institute and State University Blacksburg, VA 24061 [email protected] INTRODUCTION The calculation of the d-spacings, the angles between planes and zones, the bond lengths and angles and other important geometric relationships for a mineral can be a tedious task both for the student and the instructor, particularly when completed with the large as- sortment of trigonometric identities and algebraic formulae that are available (d. Crystal Geometry (1959), Donnay and Donnay, International Tables for Crystallography, Vol. II, Section 3, The Kynoch Press, 101-158). However, such calculations are straightforward and relatively easy to do when completed with the metrical matrix and the interactive software MATOP. Several applications of the matrix are presented below, each of which is worked out in detail and which is designed to teach you its use in the study of crystal geometry. SOME PRELIMINARY COMMENTS We begin our discussion of the matrix with a brief examination of the properties of the geometric three dimensional space, S, in which we live and in which minerals and rocks occur. For our purposes, it will be convenient to view S as the set of all vectors that radiate from a common origin to each point in space. In constructing a model for S, we chose three noncoplanar, coordinate axes denoted X, Y and Z, each radiating from the origin, O. Next, we place three nonzero vectors denoted a, band c along X, Y and Z, respectively, likewise radiating from O.
    [Show full text]
  • Primitive Cell Wigner-Seitz Cell (WS) Primitive Cell
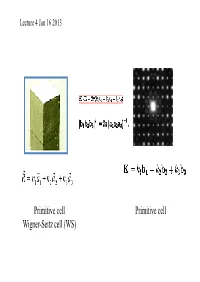
    Lecture 4 Jan 16 2013 Primitive cell Primitive cell Wigner-Seitz cell (WS) First Brillouin zone The Wigner-Seitz primitive cell of the reciprocal lattice is known as the first Brillouin zone. (Wigner-Seitz is real space concept while Brillouin zone is a reciprocal space idea). Powder cell Polymorphic Forms of Carbon Graphite – a soft, black, flaky solid, with a layered structure – parallel hexagonal arrays of carbon atoms – weak van der Waal’s forces between layers – planes slide easily over one another Miller indices Simple cubic Miller Indices Rules for determining Miller Indices: 1. Determine the intercepts of the face along the crystallographic axes, in terms of un it ce ll dimens ions. 2. Take the reciprocals 3. Clear fractions 4. Reduce to lowest terms Simple cubic d100=? Where does a protein crystallographer see the Miller indices? CtlCommon crystal faces are parallel to lattice planes • Eac h diffrac tion spo t can be regarded as a X-ray beam reflected from a lattice plane , and therefore has a unique Miller index. Miller indices A Miller index is a series of coprime integers that are inversely ppproportional to the intercepts of the cry stal face or crystallographic planes with the edges of the unit cell. It describes the orientation of a plane in the 3-D lattice with respect to the axes. The general form of the Miller index is (h, k, l) where h, k, and l are integers related to the unit cell along the a, b, c crystal axes. Irreducible brillouin zone II II II II Reciprocal lattice ghakblc The Bravais lattice after Fourier transform real space reciprocal lattice normaltthlls to the planes (vect ors ) poitints spacing between planes 1/distance between points ((y,p)actually, 2p/distance) l (distance, wavelength) 2p/l=k (momentum, wave number) BillBravais cell Wigner-SiSeitz ce ll Brillouin zone .
    [Show full text]
  • Chapter 4, Bravais Lattice Primitive Vectors
    Chapter 4, Bravais Lattice A Bravais lattice is the collection of all (and only those) points in space reachable from the origin with position vectors: n , n , n integer (+, -, or 0) r r r r 1 2 3 R = n1a1 + n2 a2 + n3a3 a1, a2, and a3 not all in same plane The three primitive vectors, a1, a2, and a3, uniquely define a Bravais lattice. However, for one Bravais lattice, there are many choices for the primitive vectors. A Bravais lattice is infinite. It is identical (in every aspect) when viewed from any of its lattice points. This is not a Bravais lattice. Honeycomb: P and Q are equivalent. R is not. A Bravais lattice can be defined as either the collection of lattice points, or the primitive translation vectors which construct the lattice. POINT Q OBJECT: Remember that a Bravais lattice has only points. Points, being dimensionless and isotropic, have full spatial symmetry (invariant under any point symmetry operation). Primitive Vectors There are many choices for the primitive vectors of a Bravais lattice. One sure way to find a set of primitive vectors (as described in Problem 4 .8) is the following: (1) a1 is the vector to a nearest neighbor lattice point. (2) a2 is the vector to a lattice points closest to, but not on, the a1 axis. (3) a3 is the vector to a lattice point nearest, but not on, the a18a2 plane. How does one prove that this is a set of primitive vectors? Hint: there should be no lattice points inside, or on the faces (lll)fhlhd(lllid)fd(parallolegrams) of, the polyhedron (parallelepiped) formed by these three vectors.
    [Show full text]
  • Symmetry and Groups, and Crystal Structures
    CHAPTER 3: SYMMETRY AND GROUPS, AND CRYSTAL STRUCTURES Sarah Lambart RECAP CHAP. 2 2 different types of close packing: hcp: tetrahedral interstice (ABABA) ccp: octahedral interstice (ABCABC) Definitions: The coordination number or CN is the number of closest neighbors of opposite charge around an ion. It can range from 2 to 12 in ionic structures. These structures are called coordination polyhedron. RECAP CHAP. 2 Rx/Rz C.N. Type Hexagonal or An ideal close-packing of sphere 1.0 12 Cubic for a given CN, can only be Closest Packing achieved for a specific ratio of 1.0 - 0.732 8 Cubic ionic radii between the anions and 0.732 - 0.414 6 Octahedral Tetrahedral (ex.: the cations. 0.414 - 0.225 4 4- SiO4 ) 0.225 - 0.155 3 Triangular <0.155 2 Linear RECAP CHAP. 2 Pauling’s rule: #1: the coodination polyhedron is defined by the ratio Rcation/Ranion #2: The Electrostatic Valency (e.v.) Principle: ev = Z/CN #3: Shared edges and faces of coordination polyhedra decreases the stability of the crystal. #4: In crystal with different cations, those of high valency and small CN tend not to share polyhedral elements #5: The principle of parsimony: The number of different sites in a crystal tends to be small. CONTENT CHAP. 3 (2-3 LECTURES) Definitions: unit cell and lattice 7 Crystal systems 14 Bravais lattices Element of symmetry CRYSTAL LATTICE IN TWO DIMENSIONS A crystal consists of atoms, molecules, or ions in a pattern that repeats in three dimensions. The geometry of the repeating pattern of a crystal can be described in terms of a crystal lattice, constructed by connecting equivalent points throughout the crystal.
    [Show full text]
  • PHZ6426 Crystal Structure
    SYMMETRY Finite geometric objects (“molecules) are symmetric with respect to a) rotations b) reflections (symmetry planes, symmetry points) c) combinatons of translations and rotations (screw axes) 2π If an object is symmetric with respect to rotation by angle φ = , it is said to have has an “n-fold rotational axis” n n=1 is a trivial case: every object is symmetric about a full revolution. Non-trivial axes have n>1. 1 Symmetries of an equilateral triangle 2 2 2 180-rotations (flips) 3’ 1’ about 22’ 3 1 3 1 2’ about 33’ about 11’ 1 3 1 2 2 3 3 2 2π 1 120 degree= rotations 3 3 2 1 3 3 3 4 2 2 1 1 An equilateral triangle is not symmetric with respect to inversion about its center. But a square is. 5 Gliding (screw) axis Rotate by 180 degrees about the axis Slide by a half-period 6 2-fold rotations can be viewed as reflections in a plane which contains a 2-fold rotation axis 7 Crystal Structure Crystal structure can be obtained by attaching atoms or groups of atoms --basis-- to lattice sites. Crystal Structure = Crystal Lattice + Basis Crystal Structure 88 Partially from Prof. C. W. Myles (Texas Tech) course presentation Building blocks of lattices are geometric figures with certain symmetries: rotational, reflectional, etc. Lattice must obey all these symmetries but, in addition, it also must obey TRANSLATIONAL symmetry Which geometric figures can be used to built a lattice? 9 10 Crystallographic Restriction Theorem: Crystal lattices have only 2-,3, 4-, and 6-fold rotational symmetries 11 B’ ma A’ n-fold axis φ-π/2 φ=2π/n a A B 1.
    [Show full text]
  • Lattice Vibrations - Phonons
    Lattice vibrations - phonons So far, we have assumed that the ions are fixed at their equilibrium positions, and we focussed on understanding the motion of the electrons in the static periodic potential created by the ions. But, of course, the ions are quantum objects that cannot be at rest in well-defined positions { this would violate Heisenberg's uncertainty principle. So they must be moving! In the following, we will assume that we are at temperatures very well below the melting temperature of the crystal, so that the ions perform small oscillations about their equilibrium positions. Of course, with increasing T the amplitude of these vibrations increases and eventually becomes large enough that the ions start moving past one another and the lattice order is progressively lost (the crystal starts to melt); our approximations will not be valid once we reach such high temperatures. Dealing with small oscillations is very nice (as you may remember from studying Lagrangian/Hamiltonian dynamics) because in the harmonic approximation, i.e. where we expand potentials up to second- order in these displacements, such classical problems can be solved exactly by mapping them to a sum of independent harmonic oscillators. Going to the quantum solution is then trivial, because it will simply be the sum of independent quantum harmonic oscillators. In this chapter we dis- cuss this solution and its implications, and for the time being we will completely forget about the electrons. We will return back to them in the next section. I assume you have already studied phonons in your undergraduate solid state physics course.
    [Show full text]
  • Crystal Structure
    Physics 927 E.Y.Tsymbal Section 1: Crystal Structure A solid is said to be a crystal if atoms are arranged in such a way that their positions are exactly periodic. This concept is illustrated in Fig.1 using a two-dimensional (2D) structure. y T C Fig.1 A B a x 1 A perfect crystal maintains this periodicity in both the x and y directions from -∞ to +∞. As follows from this periodicity, the atoms A, B, C, etc. are equivalent. In other words, for an observer located at any of these atomic sites, the crystal appears exactly the same. The same idea can be expressed by saying that a crystal possesses a translational symmetry. The translational symmetry means that if the crystal is translated by any vector joining two atoms, say T in Fig.1, the crystal appears exactly the same as it did before the translation. In other words the crystal remains invariant under any such translation. The structure of all crystals can be described in terms of a lattice, with a group of atoms attached to every lattice point. For example, in the case of structure shown in Fig.1, if we replace each atom by a geometrical point located at the equilibrium position of that atom, we obtain a crystal lattice. The crystal lattice has the same geometrical properties as the crystal, but it is devoid of any physical contents. There are two classes of lattices: the Bravais and the non-Bravais. In a Bravais lattice all lattice points are equivalent and hence by necessity all atoms in the crystal are of the same kind.
    [Show full text]
  • 02 Geometry, Reclattice.Pdf
    Geometry of Crystals Crystal is a solid composed of atoms, ions or molecules that demonstrate long range periodic order in three dimensions The Crystalline State State of Fixed Fixed Order Properties Matter Volume Shape Gas No No No Isotropic Liquid Yes No Short-range Isotropic Solid Yes Yes Short-range Isotropic (amorphous) Solid Yes Yes Long-range Anisotropic (crystalline) Atoms Lattice constants A Crystal Lattice a, b B C Not only atom, ion or molecule b positions are repetitious – there are a certain symmetry relationships in their arrangement. Crystalline Lattice structure = Basis + Crystal Lattice a a r ua One-dimensional lattice with lattice parameter a a a r ua b b b Two-dimensional lattice with lattice parameters a, b and Crystal Lattice r ua b wc Crystal Lattice Lattice vectors, lattice parameters and interaxial angles c Lattice vector a b c c Lattice parameter a b c b Interaxial angle b a a A lattice is an array of points in space in which the environment of each point is identical Crystal Lattice Lattice Not a lattice Crystal Lattice Unit cell content Coordinates of all atoms Types of atoms Site occupancy Individual displacement parameters y1 y2 y3 0 x1 x2 x3 Crystal Lattice Usually unit cell has more than one molecule or group of atoms They can be represented by symmetry operators rotation Symmetry Symmetry is a property of a crystal which is used to describe repetitions of a pattern within that crystal. Description is done using symmetry operators Rotation (about axis O) = 360°/n where n is the fold of the axis Translation n = 1, 2, 3, 4 or 6) m O i Mirror reflection Inversion Two-dimensional Symmetry Elements 1.
    [Show full text]
  • MIT 8.231 Problem 2.1 Americium
    MIT 8.231 Problem 2.1 Americium March 28, 2015 Problem The figure below shows a primitive unit cell of one crystalline form of the elementp americium. The space lattice is hexagonal with ~a1 = a~x;~a2 = 1=2a~x + 1=2 3a~y; and ~a3 = c~z. The basis is (0 0 0) , (2/3 2/3 1/4), (0 0 1/2) and (1/3 1/3 3/4). a) Find the reciprocal lattice vectors G~ . Describe in words and sketch the reciprocal lattice. b) Sketch the first Brillouin zone. Give values for the important dimensions. c) Find the structure factors associated with the points (100), (001), and (120) of the reciprocal lattice. d) What is the ratio of the scattering intensity corresponding to (120) to that corresponding to (100)? 1 Solution a) ~ ~ ~ At first we want to calculate reciprocal lattice vectors b1; b2; b3. The vectors are defined as followed: ~ a2 × a3 b1 = 2π (1) a1(a2 × a3) ~ a3 × a1 b2 = 2π (2) a1(a2 × a3) ~ a1 × a2 b3 = 2π (3) a1(a2 × a3) With the given values of ~ai we get: p 0 31 ~ 2π b1 = p @−1A (4) 3a 0 001 ~ 4π b2 = p @1A (5) 3a 0 001 2π b~ = 0 (6) 3 c @ A 1 The reciprocal lattice vector is defined as followed: ~ ~ ~ G~ = hb1 + kb2 + lb3 (7) Where h,k,l are Miller indices, with those indices Crystal planes are defined. G~ is also used for x-ray diffraction, the condition for diffraction is defined as: ~ ~ ~ G~ hkl = ∆k = k − k0 (8) This is best shown with the Ewald's Sphere.
    [Show full text]
  • Introduction to Solid State Physics
    Introduction to Solid state physics Chapter 1 Crystal Structures 晶體結構 Crystal Structures Periodic arrays of atoms Fundamental types of lattices Index system for crystal plans Simple crystal structures Direct image of atomic structure Non-ideal crystal structures Introduction In 1895, a German physicist, W. C. Roentgen discovered x-ray. In 1912 Laue developed an elementary theory of the diffraction of x-rays by a periodic array. In the second part, Friedrich and Knipping reported the first experimental observations of x-ray diffraction by crystals. 2 The work proved decisively that crystals are composed of a periodic array of atoms. The studies have been extended to include amorphous or noncrystalline solids, glasses, and liquids. The wider field is known as condensed matter physics. Periodic Arrays of Atoms An ideal crystal is constructed by the infinite repetition of identical structural units in space. The structural unit is a single atom, comprise many atoms or molecules. 晶格 The structure of all crystals can be described in terms of a lattice, with a group of atoms attached to every lattice point. The group of atoms is called the basis. 基底 The concepts of Lattice & Basis . x-ray diffraction . neutron diffraction . electron diffraction 晶格 + 基底 = 晶體結構 With this definition of the primitive translation vectors, there is no cell of smaller volume that can serve as a building block for the crystal structure. The crystal axes a1, a2, a3 form three adjacent edges of a parallelepiped. If there are lattice points only at the corners, then it is a primitive parallelepiped. Primitive Lattice Cell The parallelepiped defined by primitive axes a1, a2, a3 is called a primitive cell (Fig.
    [Show full text]