The Interpretation of Sustainability Criteria Using Game Theory Models (Sustainable Project Development with Rubik’S Cube Solution)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

002-Contents.Pdf
CubeRoot Contents Contents Contents Purple denotes upcoming contents. 1 Preface 2 Signatures of Top Cubers in the World 3 Quotes 4 Photo Albums 5 Getting Started 5.1 Cube History 5.2 WCA Events 5.3 WCA Notation 5.4 WCA Competition Tutorial 5.5 Tips to Cubers 6 Rubik's Cube 6.1 Beginner 6.1.1 LBL Method (Layer-By-Layer) 6.1.2 Finger and Toe Tricks 6.1.3 Optimizing LBL Method 6.1.4 4LLL Algorithms 6.2 Intermediate 进阶 6.2.1 Triggers 6.2.2 How to Get Faster 6.2.3 Practice Tips 6.2.4 CN (Color Neutrality) 6.2.5 Lookahead 6.2.6 CFOP Algorithms 6.2.7 Solve Critiques 3x3 - 12.20 Ao5 6.2.8 Solve Critiques 3x3 - 13.99 Ao5 6.2.9 Cross Algorithms 6.2.10 Xcross Examples 6.2.11 F2L Algorithms 6.2.12 F2L Techniques 6.2.13 Multi-Angle F2L Algorithms 6.2.14 Non-Standard F2L Algorithms 6.2.15 OLL Algorithms, Finger Tricks and Recognition 6.2.16 PLL Algorithms and Finger Tricks 6.2.17 CP Look Ahead 6.2.18 Two-Sided PLL Recognition 6.2.19 Pre-AUF CubeRoot Contents Contents 7 Speedcubing Advice 7.1 How To Get Faster 7.2 Competition Performance 7.3 Cube Maintenance 8 Speedcubing Thoughts 8.1 Speedcubing Limit 8.2 2018 Plans, Goals and Predictions 8.3 2019 Plans, Goals and Predictions 8.4 Interviewing Feliks Zemdegs on 3.47 3x3 WR Single 9 Advanced - Last Slot and Last Layer 9.1 COLL Algorithms 9.2 CxLL Recognition 9.3 Useful OLLCP Algorithms 9.4 WV Algorithms 9.5 Easy VLS Algorithms 9.6 BLE Algorithms 9.7 Easy CLS Algorithms 9.8 Easy EOLS Algorithms 9.9 VHLS Algorithms 9.10 Easy OLS Algorithms 9.11 ZBLL Algorithms 9.12 ELL Algorithms 9.13 Useful 1LLL Algorithms -

Benchmarking Beginner Algorithms for Rubik's Cube
DEGREE PROJECT, IN COMPUTER SCIENCE , FIRST LEVEL STOCKHOLM, SWEDEN 2015 Benchmarking Beginner Algorithms for Rubik's cube ANDREAS NILSSON, ANTON SPÅNG KTH ROYAL INSTITUTE OF TECHNOLOGY CSC SCHOOL Supervisor: Michael Schliephake Examiner: Örjan Ekeberg Abstract Over the years different algorithms have been developed to step-by-step solve parts of the Rubik’s cube until fi- nally reaching the unique solution. This thesis explores two commonly known beginner algorithms for solving Rubik’s cube to find how they differ in solving speed and amount of moves. The algorithms were implemented and run on a large amount of scrambled cubes to collect data. The re- sults showed that Layer-by-layer with daisy algorithm had a lower average amount of moves than the Dedmore al- gorithm. The main difference in amount of moves lies in the steps that solve the last layer of the cube. The Layer- by-layer with daisy algorithm uses only one-seventh of the time-consuming operations that Dedmore algorithm uses, which concludes that it is more suitable for speedcubing. Sammanfattning Över åren har ett antal olika algoritmer utvecklats för att steg-för-steg lösa delar av Rubik’s kub för att till sist kom- ma fram till den unika lösningen. Denna rapport utforskar två allmänt kända nybörjaralgoritmer för att lösa Rubik’s kub, för att finna hur dem skiljer sig åt i tid samt antal operationer för att nå lösningen. Algoritmerna implemen- terades och kördes på ett stort antal blandade kuber för att samla data. Resultatet visar att Lager-för-lager med daisy algoritmen hade ett lägre genomsnittligt antal förflyttning- ar jämfört med Dedmore algoritmen. -

Kurze Geschichte Des Würfels (Unknown Author)
Kurze Geschichte des Würfels (unknown author) ........................................................................................ 1 Erno Rubik .......................................................................................................................................... 1 Die Herstellung des Original-Rubik-Würfels in Ungarn ................................................................ 3 Die Rubik-Würfel-Weltmeisterschaft ............................................................................................... 6 A Rubik's Cube Chronology (Mark Longridge) .............................................................................................. 8 From five thousand to fifteen millions ....................................................................................................... 11 Toy-BUSINESS KONSUMEX .......................................................................................................................... 14 HISTORY (Nagy Olivér) ................................................................................................................................ 15 Kurze Geschichte des Würfels (unknown author) Jede Erfindung hat ein offizielles Geburtsdatum. Das Geburtsdatum des Würfels ist 1974, das Jahr, in dem der erste funktionsfähige Prototyp entstand und die erste Patentanmeldung entworfen wurde. Der Geburtsort war Budapest, die Hauptstadt Ungarns. Der Name des Erfinders ist inzwischen überall bekannt. Damals war Erno Rubik ein Dozent an der Fakultät für Innenarchitektur an der Akademie -

Breaking an Old Code -And Beating It to Pieces
Breaking an Old Code -And beating it to pieces Daniel Vu - 1 - Table of Contents About the Author................................................ - 4 - Notation ............................................................... - 5 - Time for Some Cube Math........................................................................... Error! Bookmark not defined. Layer By Layer Method................................... - 10 - Step One- Cross .................................................................................................................................. - 10 - Step Two- Solving the White Corners ................................................................................................. - 11 - Step Three- Solving the Middle Layer................................................................................................. - 11 - Step Four- Orient the Yellow Edges.................................................................................................... - 12 - Step Five- Corner Orientation ............................................................................................................ - 12 - Step Six- Corner Permutation ............................................................................................................. - 13 - Step Seven- Edge Permutation............................................................................................................ - 14 - The Petrus Method........................................... - 17 - Step One- Creating the 2x2x2 Block .................................................................................................. -

How to Solve the Rubik's Cube 03/11/2007 05:07 PM
How to Solve the Rubik's Cube 03/11/2007 05:07 PM Rubik's Revolution Rubik's Cubes & Puzzles Rubik Cube Boston's Wig Store Everything you wanted to know Rubiks Cube 4x4, Keychain & Huge selection of Rubik Cube Great selection & service Serving about the all new electronic Twist In Stock Now-Free Shipping items. the Boston area Rubik’s cube Over $75 eBay.com www.mayswigs.com www.rubiksrevolution.com AwesomeAvenue.biz Ads by Goooooogle Advertise on this site How to Solve the Rubik's Cube This page is featured under Recreation:Games:Puzzles:Rubik's Cube:Solutions in Yahoo! My Home Page | My Blog | My NHL Shootout Stats 2006-2007 There are three translations of this page: Danish (Dansk) (Word Document), Japanese (日本語) (HTML) and Portuguese (Português) (HTML). If you want to translate this page, go ahead. Send me an email when you are done and I will add your translation to this list. So you have a Rubik's Cube, and you've played with it and stared at it and taken it apart...need I go on any further? The following are two complete, fool-proof solutions to solving the cube from absolutely any legal position. Credit goes not to me, but to David Singmaster, who wrote a book in 1980, Notes on Rubik's Magic Cube, which explains pretty much all of what you need to know, plus more. Singmaster wrote about all of these moves except the move for Step 2, which I discovered independently (along with many other people, no doubt). I've updated this page to include a second solution to the cube. -

A Rubik's Cube Chronology
http://cubeman.org/cchrono.txt 02/10/2007 11:35 AM A Rubik's Cube Chronology ------------------------- Researched and maintained by Mark Longridge (c) 1996-2004 Pre-Rubik --------- Feb 2, 1960 William Gustafson files patent for Manipulatable Toy Mar 12, 1963 Gustafson receives US patent 3,081,089 1970 Uwe Meffert invents a model for research of energy flow in different shape solids (pyraminx) Apr 9, 1970 Frank Fox applies for UK patent for spherical 3x3x3 Mar 4, 1970 Larry Nichols files patent for Twizzle (2x2x2 cube) Apr 11, 1972 Nichols receives US patent 3,655,201 Jan 16, 1974 Frank Fox receives UK patent 1,344,259 Post-Rubik ---------- Spring 1974 Erno Rubik gets idea to make the cube Summer 1974 Erno Rubik solves the cube (arguably the first solver) Jan 30, 1975 Rubik applies for patent on cube Oct 12, 1976 Terutoshi Ishige Japanese Patent 55-8192 for 3x3x3 1977 Rubik's Cube starts distribution in Hungary Mar 28, 1977 Erno Rubik receives Hungarian Patent HU00170062 Aug 1978 Bela Szalai first sees cube in Hungary, later manufactures cube in U.S. (Logical Games Inc) Sept 1979 Ideal Toy buys exclusive rights to the cube for one million dollars Jan 4, 1980 Victor Toth wins pioneering cube contest in 55 sec. July 1980 MIT cube lovers group starts up Sept 1980 Omni prints article on cube in Games column Jan 12, 1981 Steven Hanson and Jeffrey Breslow file US Patent for Missing Link March 1981 Scientific American's 1st article on cube March 1981 Uwe Meffert patents the pyraminx Mar 23, 1981 First mention of Rubik's Cube in Time Magazine May 1981 Reader's Digest prints cube story July 30, 1981 Walter Moll receives German patent for Dodecahedron July 31, 1981 Cube contest featuring James G. -

Rubik's Cube Solutions
Rubik’s Cube Solutions Rubik’s Cube Solution – Useful Links http://www.geocities.com/jaapsch/puzzles/theory.htm http://www.ryanheise.com/cube/ http://peter.stillhq.com/jasmine/rubikscubesolution.html http://en.wikibooks.org/wiki/How_to_solve_the_Rubik's_Cube http://www.rubiks.com/World/~/media/Files/Solution_book_LOW_RES.ashx http://helm.lu/cube/MarshallPhilipp/index.htm Rubik’s Cube in a Scrambled State Rubik’s Cube in a Solved State – CubeTwister Front: Red, Right: Yellow, Up: Blue Back: Orange, Down: Green, Left: White Cube Colors: Red opposed to Orange, Yellow opposed to White, Blue opposed to Green Rubik’s Cube Solutions 06.12.2008 http://www.mementoslangues.fr/ Rubik’s Cube Commutators and Conjugates Introduction A Commutator is an algorithm of the form X Y X' Y', and a conjugate is an algorithm of the form X Y X', where X and Y denote arbitrary algorithms on a puzzle, and X', Y' denote their respective inverses. They are formal versions of the simple, intuitive idea of "do something to set up another task which does something useful, and undo the setup." Commutators can be used to generate algorithms that only modify specific portions of a cube, and are intuitively derivable. Many puzzle solutions are heavily or fully based on commutators. Commutator and Conjugate Notation [X, Y] is a commonly used notation to represent the sequence X Y X' Y'. [X: Y] is a well-accepted representation of the conjugate X Y X'. Since commutators and conjugates are often nested together, Lucas Garron has proposed the following system for compact notation: Brackets denote an entire algorithm, and within these, the comma delimits a commutator, and a colon or a semicolon a conjugate. -

The Cubing Community Megasurvey 2021 Acknowledgements
THE CUBING COMMUNITY MEGASURVEY 2021 ACKNOWLEDGEMENTS This work follows in the footsteps of the r/Cubers tradition of yearly Megasurveys, of which this is the fifth instalment. For the first time we've been able to integrate the responses and experience of our colleagues from China, whose communities do not always have access to the same online spaces. We're happy to present the results of this survey as a whole, reuniting these two big communities The following people contributed to this project: You guys were awesome, The r/Cubers mods: have been running the survey for the • welcoming and super supportive past 5 years, wrote and managed the bulk of it and proofread this during the whole analysis process! whole monster of a document. Thank you naliuj, gilzu, stewy, greencrossonleft, topppits, g253, pianocube93 and leinadium! It's been a blast discussing with you, Ruimin Yan / CubeRoot : provided great ideas for the • getting your ideas and seeing you recruit survey, helped coordinate between the east and the west, a thousand people in a matter of days! leveraged his online standing and following to gather all respondents across China and re-translated most this document • Justin Yang: translated the survey into mandarin and helped You have no excuse for speaking re-translate answers during the re-combination and cleanup flawless french (on top of all phase your other languages) at your ridiculously young age! About the author of this document: Basilio Noris is an older cuber, who has spent the past 15 years working on understanding and measuring human behaviour. He spends way too much time playing with data and looking for ways in which to present it. -

WCA Regulations and Guidelines WCA Regulations Committee
WCA Regulations and Guidelines WCA Regulations Committee Règlement WCA Version : 1 Janvier 2018 [wca-regulations-translations:886ca87] Notes Traduction La traduction de ce document a été réalisée par Philippe Virouleau et mise à jour en 2018 par Jules Desjardin, et s'appuie sur les précédents travaux de Guillaume Erbibou, Pierre Calendini, et Gilles Roux. Des efforts sont faits pour que cette traduction soit constamment à jour, elle n'a rien d'officielle bien que présente sur le site officiel de la WCA. Elle est fournie à titre informatif : seule la version anglaise fait foi en cas de différence. Règlement et Recommandations WCA Le Règlement WCA contient l'ensemble des règles qui s'appliquent lors de toutes les compétitions officielles reconnues par la World Cube Association. Le Règlement WCA est également complémenté par les Recommandations WCA. Le Règlement devrait être considéré comme un document complet, mais les Recommandations contiennent des informations et explications additionnelles. Formulation L'utilisation du genre masculin a été adoptée afin de faciliter la lecture. Elle n'a aucune intention discriminatoire. L'utilisation des mots "doit", "ne doit pas", "devrait", "ne devrait pas", et "peut" correspondent respectivement aux mots "must", "must not", "should", "should not", et "may" tels que définis dans le RFC 2119. Informations sur internet Site internet de la World Cube Association : www.worldcubeassociation.org. Documents originaux du Règlement WCA : www.worldcubeassociation.org/regulations. Règlement WCA au format PDF. Sources Le développement du Règlement et des Recommandations est public sur GitHub. Le développement des traductions est public sur GitHub. La traduction française est maintenue dans ce dépôt. -
Puzzle Patents 07/08/2007 04:31 PM
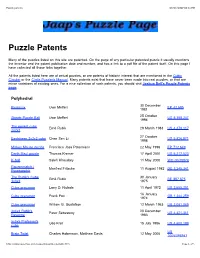
Puzzle patents 07/08/2007 04:31 PM Puzzle Patents Many of the puzzles listed on this site are patented. On the page of any particular patented puzzle it usually mentions the inventor and the patent publication date and number, and has a link to a pdf file of the patent itself. On this page I have collected all those links together. All the patents listed here are of actual puzzles, or are patents of historic interest that are mentioned in the Cubic Circular or the Circle Puzzler's Manual. Many patents exist that have never been made into real puzzles, or that are minor variations of existing ones. For a nice collection of such patents, you should visit Joshua Bell's Puzzle Patents page. Polyhedral 30 December Pyraminx Uwe Meffert EP 42,695 1981 25 October Skewb Puzzle Ball Uwe Meffert US 5,358,247 1994 The pocket cube Ernö Rubik 29 March 1983 US 4,378,117 2x2x2 27 October Eastsheen 2x2x2 cube Chen Sen Li US 5,826,871 1998 Mickey Mouse puzzle Francisco Josa Patermann 22 May 1996 EP 712,649 Darth Maul puzzle Thomas Kremer 17 April 2001 US 6,217,023 K-ball Saleh Khoudary 11 May 2000 WO 00/25874 Figurenmatch / Manfred Fritsche 11 August 1982 DE 3,245,341 Pyramorphix The Rubik's Cube 30 January Ernö Rubik BE 887,875 3x3x3 1975 Cube precursor Larry D. Nichols 11 April 1972 US 3,655,201 16 January Cube precursor Frank Fox GB 1,344,259 1974 Cube precursor William G. Gustafson 12 March 1963 US 3,081,089 4x4x4 Rubik's 20 December Peter Sebesteny US 4,421,311 Revenge 1983 5x5x5 Professor's Udo Krell 15 July 1986 US 4,600,199 cube US Brain Twist Charles Hoberman, Matthew Davis 12 May 2005 2005/098947 http://www.geocities.com/jaapsch/puzzles/patents.htm Page 1 of 5 Puzzle patents 07/08/2007 04:31 PM 16 January WO Jackpot / Platypus Yusuf Seyhan 2003 03/004117 Alexander's Star Adam Alexander 26 March 1985 US 4,506,891 Dogic Zoltan and Robert Vecsei 28 July 1998 HU 214,709 Impossiball William O. -

Full Beacher
THE TM 911 Franklin Street Weekly Newspaper Michigan City, IN 46360 Volume 36, Number 33 Thursday, August 20, 2020 An Artist’s Voice Takes Flight by Linda Weigel Editor’s note — This is the latest in an ongoing series that profi les women artists in the region. “In order to see birds it is necessary to become a part of the silence.” Robert Lynd Kristina Knowski knows how to be- come a part of the silence. As an avid birdwatcher and stunning illustrator of birds, she exudes a special joy when dis- cussing her love of being in the fi eld and the challenge of identifying species, es- pecially in the Michiana region. Born in Justice, Ill., she spent most of her childhood in Joliet. She was always interested in art, a sketchbook by her side. Interested in attending art school, she took summer classes at various col- leges while still in middle and high school. “I would always ask for new sketch- books for my birthday,” she said, “as I went from going through one book a year to two, to three, etc.” She didn’t start painting until high school. “Completed works” during her childhood primarily consisted of colored pencil or rendered graphite. “I had a lot of trouble completing a project,” she said, “as I tend to be a per- fectionist, and I feel like I needed to redo a halfway completed work. I had to get over that barrier in college.” She attended Joliet Junior College, Western Illinois University and the American Academy of Art during sum- mers off from school. -

Rubik's Cube Study
Rubik’s Cube Study Hwa Chong Institution (High School) Project Work 2020 - Category 8 (Mathematics) Written Report Group 8-21 1A1 - Alastair Chua Wei Jie (1) - Leader 1P2 - John Pan Zhenda (11) - Member 1P2 - Li Junle Tristen (16) - Member 1 Contents 1.0 Introduction 3 1.1 Rationale 3 1.2 Research Questions 3 2.0 Mechanics 3 2.0.1 Orientation of Colours 4 2.1 Notations 4 2.2 Intended Methodology 5 3.0 Literature Review 5 3.0.1 History of Rubik’s Cube 6 3.1 Background 7 4.0 Findings 8 4.1 Factors Affecting Speedcubing 8 4.2 Discovery of God’s Number 9 4.3 Formation of Algorithms 11 5.0 Conclusions 12 6.0 Possibility of Project Extension 13 7.0 References 13 2 1.0 Introduction The Rubik’s Cube has been a very well-known toy for several years, challenging for most, but a piece of cake for the intelligent few. As of January 2009, 350 million cubes had been sold worldwide, thus widely regarded as the world’s best selling toy. It is a 3D combination puzzle invented in 1974, by Ernö Rubik. 1.1 Rationale The Rubik’s Cube is not only a three-dimensional puzzle to toy with for fun, but also a source of mathematical concepts and calculations. Through this project, we intend to learn more about the mechanics of the Rubik’s Cube, and get more in-depth knowledge about how it works and the mathematics behind it. We also aim to discover more about the different types of cubes, including studying their mechanisms and algorithms.