DOCSLIB.ORG

Control Systems

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Control Systems Control Systems en.wikibooks.org December 26, 2019 On the 28th of April 2012 the contents of the English as well as German Wikibooks and Wikipedia projects were licensed under Creative Commons Attribution-ShareAlike 3.0 Unported license. A URI to this license is given in the list of figures on page 345. If this document is a derived work from the contents of one of these projects and the content was still licensed by the project under this license at the time of derivation this document has to be licensed under the same, a similar or a compatible license, as stated in section 4b of the license. The list of contributors is included in chapter Contributors on page 337. The licenses GPL, LGPL and GFDL are included in chapter Licenses on page 355, since this book and/or parts of it may or may not be licensed under one or more of these licenses, and thus require inclusion of these licenses. The licenses of the figures are given in the list of figures on page 345. This PDF was generated by the LATEX typesetting software. The LATEX source code is included as an attachment (source.7z.txt) in this PDF file. To extract the source from the PDF file, you can use the pdfdetach tool including in the poppler suite, or the http://www. pdflabs.com/tools/pdftk-the-pdf-toolkit/ utility. Some PDF viewers may also let you save the attachment to a file. After extracting it from the PDF file you have to rename it to source.7z. To uncompress the resulting archive we recommend the use of http://www.7-zip.org/. The LATEX source itself was generated by a program written by Dirk Hünniger, which is freely available under an open source license from http://de.wikibooks.org/wiki/Benutzer:Dirk_Huenniger/wb2pdf. Contents 1 Preface 3 2 Introduction 5 2.1 This Wikibook ................................. 5 2.2 What are Control Systems? .......................... 5 2.3 Classical and Modern .............................. 6 2.4 Who is This Book For? ............................. 7 2.5 What are the Prerequisites? .......................... 7 2.6 How is this Book Organized? ......................... 8 2.7 Differential Equations Review ......................... 9 2.8 History ...................................... 11 2.9 Branches of Control Engineering ....................... 12 2.10 MATLAB .................................... 13 2.11 About Formatting ................................ 14 3 System Identification 17 3.1 Systems ..................................... 17 3.2 System Properties ................................ 17 3.3 Initial Time ................................... 17 3.4 Additivity .................................... 18 3.5 Homogeneity .................................. 19 3.6 Linearity ..................................... 20 3.7 Memory ..................................... 21 3.8 Causality ..................................... 21 3.9 Time-Invariance ................................. 22 3.10 LTI Systems ................................... 22 3.11 Lumpedness ................................... 22 3.12 Relaxed ..................................... 23 3.13 Stability ..................................... 23 3.14 Inputs and Outputs ............................... 23 4 Digital and Analog 25 4.1 Digital and Analog ............................... 25 4.2 Analog ...................................... 27 4.3 Digital ...................................... 28 4.4 Hybrid Systems ................................. 29 4.5 Continuous and Discrete ............................ 30 4.6 Sampling and Reconstruction ......................... 30 III Contents 5 System Metrics 33 5.1 System Metrics ................................. 33 5.2 Standard Inputs ................................. 33 5.3 Steady State ................................... 35 5.4 Target Value ................................... 36 5.5 Rise Time .................................... 37 5.6 Percent Overshoot ............................... 37 5.7 Steady-State Error ............................... 38 5.8 Settling Time .................................. 38 5.9 System Order .................................. 38 5.10 System Type .................................. 39 5.11 Visually ..................................... 41 6 System Modeling 43 6.1 The Control Process .............................. 43 6.2 External Description .............................. 43 6.3 Internal Description ............................... 44 6.4 Complex Descriptions .............................. 45 6.5 Representations ................................. 45 6.6 Analysis ..................................... 45 6.7 Modeling Examples ............................... 47 6.8 Manufacture ................................... 47 7 Transforms 49 7.1 Transforms .................................... 49 7.2 Laplace Transform ............................... 49 7.3 Fourier Transform ................................ 58 7.4 Complex Plane ................................. 59 7.5 Euler's Formula ................................. 59 7.6 MATLAB .................................... 60 7.7 Further reading ................................. 60 8 Transfer Functions 61 8.1 Transfer Functions ............................... 61 8.2 Impulse Response ................................ 61 8.3 Convolution ................................... 65 8.4 Convolution Theorem .............................. 66 8.5 Using the Transfer Function .......................... 66 8.6 Frequency Response .............................. 68 9 Sampled Data Systems 71 9.1 Ideal Sampler .................................. 71 9.2 Geometric Series ................................ 71 9.3 The Star Transform ............................... 73 9.4 The Z-Transform ................................ 74 9.5 Star ↔ Z ..................................... 76 9.6 Z ↔ Fourier ................................... 80 9.7 Reconstruction ................................. 81 IV Contents 9.8 Further reading ................................. 87 10 System Delays 89 10.1 Delays ...................................... 89 10.2 Time Shifts ................................... 89 10.3 Delays and Stability .............................. 90 10.4 Delay Margin .................................. 90 10.5 Transform-Domain Delays ........................... 91 10.6 Modified Z-Transform ............................. 92 11 Poles and Zeros 93 11.1 Poles and Zeros ................................. 93 11.2 Time-Domain Relationships .......................... 93 11.3 What are Poles and Zeros ........................... 94 11.4 Effects of Poles and Zeros ........................... 95 11.5 Second-Order Systems ............................. 95 11.6 Higher-Order Systems ............................. 96 12 State-Space Equations 97 12.1 Time-Domain Approach ............................ 97 12.2 State-Space ................................... 98 12.3 State Variables ................................. 99 12.4 Multi-Input, Multi-Output ........................... 99 12.5 State-Space Equations ............................. 100 12.6 Obtaining the State-Space Equations . 103 12.7 State-Space Representation . 105 12.8 Discretization .................................. 107 12.9 Note on Notations ............................... 108 12.10 MATLAB Representation . 108 13 Solutions for Linear Systems 111 13.1 State Equation Solutions ............................ 111 13.2 Solving for x(t) With Zero Input . 111 13.3 Solving for x(t) With Non-Zero Input . 112 13.4 State-Transition Matrix ............................ 113 14 Time-Variant System Solutions 119 14.1 General Time Variant Solution . 119 14.2 Time-Variant, Zero Input . 120 14.3 Time-Variant, Non-zero Input . 124 15 Digital State-Space 125 15.1 Digital Systems ................................. 125 15.2 Digital Systems ................................. 125 15.3 Relating Continuous and Discrete Systems . 126 15.4 Converting Difference Equations . 128 15.5 Solving for x[n] ................................. 129 15.6 Time Variant Solutions ............................. 130 15.7 MATLAB Calculations ............................. 131 V Contents 16 Eigenvalues and Eigenvectors 133 16.1 Eigenvalues and Eigenvectors . 133 16.2 Characteristic Equation ............................ 133 16.3 Exponential Matrix Decomposition . 135 16.4 Non-Unique Eigenvalues ............................ 137 16.5 Equivalence Transformations . 139 17 MIMO Systems 141 17.1 Multi-Input, Multi-Output . 141 17.2 State-Space Representation . 141 17.3 Transfer Function Matrix ............................ 142 17.4 Discrete MIMO Systems ............................ 144 18 System Realization 147 18.1 Realization .................................... 147 18.2 Realization Conditions ............................. 147 18.3 Realizing the Transfer Matrix . 147 19 Gain 149 19.1 What is Gain? .................................. 149 19.2 Responses to Gain ............................... 150 19.3 Gain and Stability ............................... 150 20 Block Diagrams 151 20.1 Systems in Series ................................ 151 20.2 Systems in Parallel ............................... 154 20.3 State Space Model ............................... 154 20.4 Adders and Multipliers ............................. 156 20.5 Simplifying Block Diagrams . 156 20.6 External links .................................. 157 21 Feedback Loops 159 21.1 Feedback ..................................... 159 21.2 Basic Feedback Structure ............................ 159 21.3 Negative vs Positive Feedback . 160 21.4 Feedback Loop Transfer Function . 162 21.5 Open Loop vs Closed Loop . 164 21.6 Placement of a Controller
Load more

Recommended publications
  • Control Engineering for High School Students and Teachers: an Online Platform Development
    Control Engineering for High School Students and Teachers: An Online Platform Development Farhad Farokhi and Iman Shames Contents Report ............................................ 1 1 Introduction . 1 2 Courses . 1 3 Interviews . 2 4 Educational games . 3 5 Remote laboratory . 4 6 Conclusions and future work . 5 Appendix .......................................... 6 A Example course 1: Feedback theory . 6 B Example course 2: Models . 9 C Example course 3: On/off control . 12 D Remote laboratory (RLAB) manual . 13 1 Introduction Based on our teen years and feedback from many of our colleagues and friends, we believe that the control engineering, although being a major building block of automated system in many processes and infrastructures, is a fairly alien subject to the students, parents, and teachers. Therefore, there is a need for introducing feedback control and its application to high school students and their teachers to recruit the next generation of engineers and scientists in this field. We also believe that the academic community has a responsibility to disseminate the information cheaply, if not freely, to a wide range of interested audience, be it students, parents, or teachers, across the globe. This way, we can guarantee that people from different socio- economic backgrounds and in different countries can make informed decisions regarding their careers and those of their friends and families. Motivated by these needs, in this project, we have attempted at developing an online platform for the students and their educators to read about the control engineering, watch lectures by researchers from academia and industry, access interviews with successful people in the control engineering community, and play online games to test their understanding and to possibly learn about the applications of the automatic control.
    [Show full text]
  • EE C128 Chapter 10
    Lecture abstract EE C128 / ME C134 – Feedback Control Systems Topics covered in this presentation Lecture – Chapter 10 – Frequency Response Techniques I Advantages of FR techniques over RL I Define FR Alexandre Bayen I Define Bode & Nyquist plots I Relation between poles & zeros to Bode plots (slope, etc.) Department of Electrical Engineering & Computer Science st nd University of California Berkeley I Features of 1 -&2 -order system Bode plots I Define Nyquist criterion I Method of dealing with OL poles & zeros on imaginary axis I Simple method of dealing with OL stable & unstable systems I Determining gain & phase margins from Bode & Nyquist plots I Define static error constants September 10, 2013 I Determining static error constants from Bode & Nyquist plots I Determining TF from experimental FR data Bayen (EECS, UCB) Feedback Control Systems September 10, 2013 1 / 64 Bayen (EECS, UCB) Feedback Control Systems September 10, 2013 2 / 64 10 FR techniques 10.1 Intro Chapter outline 1 10 Frequency response techniques 1 10 Frequency response techniques 10.1 Introduction 10.1 Introduction 10.2 Asymptotic approximations: Bode plots 10.2 Asymptotic approximations: Bode plots 10.3 Introduction to Nyquist criterion 10.3 Introduction to Nyquist criterion 10.4 Sketching the Nyquist diagram 10.4 Sketching the Nyquist diagram 10.5 Stability via the Nyquist diagram 10.5 Stability via the Nyquist diagram 10.6 Gain margin and phase margin via the Nyquist diagram 10.6 Gain margin and phase margin via the Nyquist diagram 10.7 Stability, gain margin, and
    [Show full text]
  • Download Chapter 161KB
    Memorial Tributes: Volume 3 HENDRIK WADE BODE 50 Copyright National Academy of Sciences. All rights reserved. Memorial Tributes: Volume 3 HENDRIK WADE BODE 51 Hendrik Wade Bode 1905–1982 By Harvey Brooks Hendrik Wade Bode was widely known as one of the most articulate, thoughtful exponents of the philosophy and practice of systems engineering—the science and art of integrating technical components into a coherent system that is optimally adapted to its social function. After a career of more than forty years with Bell Telephone Laboratories, which he joined shortly after its founding in 1926, Dr. Bode retired in 1967 to become Gordon McKay Professor of Systems Engineering (on a half-time basis) in what was then the Division of Engineering and Applied Physics at Harvard. He became professor emeritus in July 1974. He died at his home in Cambridge on June 21, 1982, at the age of seventy- six. He is survived by his wife, Barbara Poore Bode, whom he married in 1933, and by two daughters, Dr. Katharine Bode Darlington of Philadelphia and Mrs. Anne Hathaway Bode Aarnes of Washington, D.C. Hendrik Bode was born in Madison, Wisconsin, on December 24, 1905. After attending grade school in Tempe, Arizona, and high school in Urbana, Illinois, he went on to Ohio State University, from which he received his B.A. in 1924 and his M.A. in 1926, both in mathematics. He joined Bell Labs in 1926 to work on electrical network theory and the design of electric filters. While at Bell, he also pursued graduate studies at Columbia University, receiving his Ph.D.
    [Show full text]
  • Measuring the Control Loop Response of a Power Supply Using an Oscilloscope ––
    Measuring the Control Loop Response of a Power Supply Using an Oscilloscope –– APPLICATION NOTE MSO 5/6 with built-in AFG AFG Signal Injection Transformers J2100A/J2101A VIN VOUT TPP0502 TPP0502 5Ω RINJ T1 Modulator R1 fb – comp R2 + + VREF – Measuring the Control Loop Response of a Power Supply Using an Oscilloscope APPLICATION NOTE Most power supplies and regulators are designed to maintain a Introduction to Frequency Response constant voltage over a specified current range. To accomplish Analysis this goal, they are essentially amplifiers with a closed feedback loop. An ideal supply needs to respond quickly and maintain The frequency response of a system is a frequency-dependent a constant output, but without excessive ringing or oscillation. function that expresses how a reference signal (usually a Control loop measurements help to characterize how a power sinusoidal waveform) of a particular frequency at the system supply responds to changes in output load conditions. input (excitation) is transferred through the system. Although frequency response analysis may be performed A generalized control loop is shown in Figure 1 in which a using dedicated equipment, newer oscilloscopes may be sinewave a(t) is applied to a system with transfer function used to measure the response of a power supply control G(s). After transients due to initial conditions have decayed loop. Using an oscilloscope, signal source and automation away, the output b(t) becomes a sinewave but with a different software, measurements can be made quickly and presented magnitude B and relative phase Φ. The magnitude and phase as familiar Bode plots, making it easy to evaluate margins and of the output b(t) are in fact related to the transfer function compare circuit performance to models.
    [Show full text]
  • Affine Laws and Learning Approaches for Witsenhausen
    Special Topics Seminar Affine Laws and Learning Approaches for Witsenhausen Counterexample Hajir Roozbehani Dec 7, 2011 Outline I Optimal Control Problems I Affine Laws I Separation Principle I Information Structure I Team Decision Problems I Witsenhausen Counterexample I Sub-optimality of Affine Laws I Quantized Control I Learning Approach Linear Systems Discrete Time Representation In a classical multistage stochastic control problem, the dynamics are x(t + 1) = Fx(t) + Gu(t) + w(t) y(t) = Hx(t) + v(t); where v(t) and y(t) are independent sequences of random variables and u(t) = γ(y(t)) is the control law (or decision rule). A cost function J(γ; x(0)) is to be minimized. Linear Systems Discrete Time Representation In a classical multistage stochastic control problem, the dynamics are x(t + 1) = Fx(t) + Gu(t) + w(t) y(t) = Hx(t) + v(t); where v(t) and y(t) are independent sequences of random variables and u(t) = γ(y(t)) is the control law (or decision rule). A cost function J(γ; x(0)) is to be minimized. Success Stories with Affine Laws LQR Consider a linear dynamical system n m x(t + 1) = Fx(t) + Gu(t); x(t) 2 R ; u(t) 2 R with complete information and the task of finding a pair (x(t); u(t)) that minimizes the functional T X 0 0 J(u(t)) = [x(t) Qx(t) + u(t) Ru(t)]; t=0 subject to the described dynamical constraints and for Q > 0; R > 0. This is a convex optimization problem with an affine solution: 0 u∗(t) = −R−1B P(t)x(t); where P(t) is to be found by solving algebraic Riccati equations.
    [Show full text]
  • Symbolic Analysis of Linear Electric Circuits with Maxima
    Dejan V. Tošić, Milka M. Potrebić, Symbolic analysis of linear electric circuits with Maxima CAS, Application of Free Software and Open Hardware, PSSOH 2019, International Conference, University of Belgrade – School of Electrical Engineering, Belgrade, Serbia, Oct. 26, 2019. http://pssoh.etf.bg.ac.rs/ Symbolic analysis of linear electric circuits with Maxima CAS Dejan V. Tošić, Milka M. Potrebić University of Belgrade – School of Electrical Engineering, Belgrade, Serbia [email protected], [email protected] Application of Free Software and Open Hardware, PSSOH 2019, International Conference, University of Belgrade – School of Electrical Engineering, Belgrade, Serbia, Oct. 26, 2019. http://pssoh.etf.bg.ac.rs/ Dejan V. Tošić, Milka M. Potrebić, Symbolic analysis of linear electric circuits with Maxima CAS, Application of Free Software and Open Hardware, PSSOH 2019, International Conference, University of Belgrade – School of Electrical Engineering, Belgrade, Serbia, Oct. 26, 2019. http://pssoh.etf.bg.ac.rs/ What is symbolic simulation ● Symbolic simulation or analysis is a formal technique to calculate the behavior or a characteristic of a system (e.g. digital system, electronic circuit, or continuous-time system) with an independent variable (sample index, time, or frequency), the dependent variables (sample values, signals, voltages, and currents), and (some or all) the element values represented by symbols. ● A symbolic simulator is a computer program that receives the system description as input and can automatically carry out the symbolic analysis and thus generate the symbolic expression for the desired system characteristic. ● P. Lin, Symbolic Network Analysis. Amsterdam, The Netherlands: Elsevier, 1991. ● G. Gielen and W. Sansen, Symbolic Analysis for Automated Design of Analog Integrated Circuits.
    [Show full text]
  • Mirostat:Aneural Text Decoding Algorithm That Directly Controls Perplexity
    Published as a conference paper at ICLR 2021 MIROSTAT:ANEURAL TEXT DECODING ALGORITHM THAT DIRECTLY CONTROLS PERPLEXITY Sourya Basu∗ Govardana Sachitanandam Ramachandrany Nitish Shirish Keskary Lav R. Varshney∗;y ∗Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign ySalesforce Research ABSTRACT Neural text decoding algorithms strongly influence the quality of texts generated using language models, but popular algorithms like top-k, top-p (nucleus), and temperature-based sampling may yield texts that have objectionable repetition or incoherence. Although these methods generate high-quality text after ad hoc pa- rameter tuning that depends on the language model and the length of generated text, not much is known about the control they provide over the statistics of the output. This is important, however, since recent reports show that humans pre- fer when perplexity is neither too much nor too little and since we experimen- tally show that cross-entropy (log of perplexity) has a near-linear relation with repetition. First we provide a theoretical analysis of perplexity in top-k, top-p, and temperature sampling, under Zipfian statistics. Then, we use this analysis to design a feedback-based adaptive top-k text decoding algorithm called mirostat that generates text (of any length) with a predetermined target value of perplexity without any tuning. Experiments show that for low values of k and p, perplexity drops significantly with generated text length and leads to excessive repetitions (the boredom trap). Contrarily, for large values of k and p, perplexity increases with generated text length and leads to incoherence (confusion trap). Mirostat avoids both traps.
    [Show full text]
  • Università Degli Studi Di Padova Padua
    Università degli Studi di Padova Padua Research Archive - Institutional Repository Negative Feedback, Amplifiers, Governors, and More Original Citation: Availability: This version is available at: 11577/3257394 since: 2018-02-15T15:55:12Z Publisher: Institute of Electrical and Electronics Engineers Inc. Published version: DOI: 10.1109/MIE.2017.2726244 Terms of use: Open Access This article is made available under terms and conditions applicable to Open Access Guidelines, as described at http://www.unipd.it/download/file/fid/55401 (Italian only) (Article begins on next page) Historical by Massimo Guarnieri Negative Feedback, Amplifiers, Governors, and More Massimo Guarnieri he invention of the negative feed- Henry (1797–1878) and Samuel Morse (1873–1961), the holder of a similar back amplifier by Harold S. Black (1791–1872) and was very successful patent of 1916. In the final courtroom T (1898–1983) in 1928 is consid- against the attenuation of telegraph digi- battle in 1934, the Supreme Court ruled ered one of the great achievements in tal signals. in favor of De Forest. Meanwhile, in electronics. In fact, it is listed among Telephone lines, which started to 1922, Armstrong introduced the su- the IEEE Milestones, where it is cred- be laid in the 1880s, were also prone perregenerative receiver, which used ited to Bell Labs. Black was hired by to attenuation. However, their signals a larger part of the signal to obtain Western Electric in 1921 and as- were analog, so regeneration based on an even higher amplification (gain signed to work on the Type C system, a just an electrochemical battery and around 1 million).
    [Show full text]
  • Eric Serge Sanches
    PROGRAMA FRANCISCO EDUARDO MOURÃO SABOYA DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA ESCOLA DE ENGENHARIA UNIVERSIDADE FEDERAL FLUMINENSE Tese de Doutorado UMA CONTRIBUIÇÃO AO ESTUDO E CONTROLE DE UM MOTOR DE RELUTÂNCIA CHAVEADO DE FLUXO AXIAL COM UM SÓ ESTATOR ERIC SERGE SANCHES DEZEMBRO DE 2015 ERIC SERGE SANCHES UMA CONTRIBUIÇÃO AO ESTUDO E CONTROLE DE UM MOTOR DE RELUTÂNCIA CHAVEADO DE FLUXO AXIAL COM UM SÓ ESTATOR Tese de Doutorado apresentada ao Programa Francisco Eduardo Mourão Saboya de Pós - Graduação em Engenharia Mecânica da UFF como parte dos requisitos para a obtenção do título de Doutor em Ciências em Engenharia Mecânica Orientador: Prof. Dr. José Andrés Santisteban Larrea (PGMEC/UFF ) UNIVERSIDADE FEDERAL FLUMINENSE NITERÓI, 16 DE DEZEMBRO DE 2015 À minha família e aos amigos que direta ou indiretamente contribuíram para a concretização deste sonho. AGRADECIMENTOS Ao Professor José Andrés Santisteban Larrea um agradecimento do fundo do meu coração pelo auxílio inestimável na realização deste sonho, pois quando perdia o rumo ele me indicava o norte. À Professora Stella Maris pelo apoio prestado nos primeiros passos desta empreitada. Aos Professores do Programa de Pós-Graduação em Engenharia Mecânica (PGMEC) da Universidade Federal Fluminense pelos ensinamentos ministrados. Ao Professores do Departamento de Engenharia Elétrica da Universidade Federal Fluminense, em especial Márcio Sens, Guilherme Sotelo e Vitor Hugo, pelo apoio e incentivo prestados durante a realização desta pesquisa. Aos amigos engenheiros e técnicos Itamar e equipe (AMRJ), Almir, Fabrício, Silvio, Amaro, Branquinho, Pedro, Medeiros, Christopher Grey, Roberto Brandão, Gustavo e José Carlos, pela ajuda na parte experimental desta pesquisa e constante incentivo.
    [Show full text]
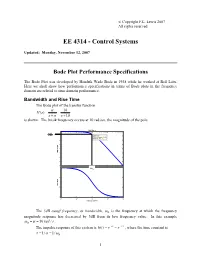
  • Bode Plot Performance Specifications
    © Copyright F.L. Lewis 2007 All rights reserved EE 4314 - Control Systems Updated: Monday, November 12, 2007 Bode Plot Performance Specifications The Bode Plot was developed by Hendrik Wade Bode in 1938 while he worked at Bell Labs. Here we shall show how performance specifications in terms of Bode plots in the frequency domain are related to time domain performance. Bandwidth and Rise Time The Bode plot of the transfer function α 10 Hs()== ss++α 10 is shown. The break frequency occurs at 10 rad/sec, the magnitude of the pole. Bode Diagram 0 -3db -5 System: sys Frequency (rad/sec): 9.98 Magnitude (dB): -3 -10 -15 -20 Magnitude (dB)Magnitude -25 -30 -35 -40 0 ωB -30 Phase (deg) -60 -90 -1 0 1 2 3 10 10 10 10 10 Frequency (rad/sec) The 3dB cutoff frequency, or bandwidth, ωB is the frequency at which the frequency magnitude response has decreased by 3dB from its low frequency value. In this example ωB ==α 10rad / s . The impulse response of this system is ht()== e−−αtt e /τ , where the time constant is τ ==1/αω 1/ B . 1 The step response rise time is given by tr = 2.2τ . The settling time is ts = 5τ . The time constant is inversely related to the bandwidth. Therefore, as bandwidth increases, the system response becomes faster. COMPLEX POLE PAIR A transfer function with a complex pair of poles and no finite zeros can be written as ω 2 ω 2 ω 2 H (s) = n = n ≡ n . 2 2 2 2 s + 2αs + ω n s + 2ζω n s + ω n Δ(s) The numerator is chosen to scale the transfer function so that the DC gain (e.g.
    [Show full text]
  • Arxiv:1809.08747V1 [Quant-Ph] 24 Sep 2018 Adit N Wsaepwrhnln.Wt Respect with Power-Handling
    Design of an on-chip superconducting microwave circulator with octave bandwidth Benjamin J. Chapman,1,2, ∗ Eric I. Rosenthal,1, 2 and K. W. Lehnert1, 2 1JILA, National Institute of Standards and Technology and the University of Colorado, Boulder, Colorado 80309, USA 2 Department of Physics, University of Colorado, Boulder, Colorado 80309, USA (Dated: September 25, 2018) We present a design for a superconducting, on-chip circulator composed of dynamically modulated transfer switches and delays. Design goals are set for the multiplexed readout of superconducting qubits. Simulations of the device show that it allows for low-loss circulation (insertion loss < 0.35 dB and isolation > 20 dB) over an instantaneous bandwidth of 2.3 GHz. As the device is estimated to be linear for input powers up to −65 dBm, this design improves on the bandwidth and power- handling of previous superconducting circulators [1–3] by over a factor of 50, making it ideal for integration with broadband quantum limited amplifiers [4–6]. I. INTRODUCTION to bandwidth and linearity, this represents a 50-fold im- provement over other near-lossless superconducting cir- Sophisticated signal-processing often requires that culators [1–3], well-suited for integration with broadband Lorentz reciprocity—the scattering symmetry of an quantum-limited amplifiers [4–6]. electromagnetic system under exchange of source and detector—be broken. In particular, directionally-routing propagating electromagnetic modes without adding noise II. THEORY OF OPERATION or incurring loss is vital for quantum information process- ing with superconducting circuits. The proposed circulator is composed of two transfer Although Maxwell’s equations place no restrictions on switches connected by a pair of delay lines (Fig.
    [Show full text]
  • KALMAN FILTERING Theory and Practice Using Matlabw
    KALMAN FILTERING KALMAN FILTERING Theory and Practice Using MATLABw Third Edition MOHINDER S. GREWAL California State University at Fullerton ANGUS P. ANDREWS Rockwell Science Center (retired) Copyright # 2008 by John Wiley & Sons, Inc. All rights reserved Published by John Wiley & Sons, Inc., Hoboken, New Jersey Published simultaneously in Canada No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4470, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http:// www.wiley.com/go/permission. Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or complete- ness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. The advice and strategies contained herein may not be suitable for your situation. You should consult with a professional where appropriate.
    [Show full text]