DOCSLIB.ORG

T E S Is Do Ct O

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
T E S Is Do Ct O Modelling and Structural Analysis of historical masonry systems including vaulted structure tesis doctoral realizada por: masonry sytems including vaulted structure vaultedmasonry including sytems Modelling and Structural Analysis ofAnalysis historical and Structural Modelling Yohei Endo DOCTORAL Yohei Endo Yohei TESIS realizada por dirigida por: Pere Roca i Fabregat doctoral Luca Pelà tesis 5 ,201 Barcelona, Mayo de 2015 Mayo Universitat Politècnica de Catalunya Departament d´Enginyeria de la Construcció Curso académico: 2014-2015 Acta de calificación de tesis doctoral Nombre y apellidos Yohei Endo Programa de doctorado Ingenieria de la Construccion Unidad estructural responsable del programa Departamento de Ingenieria de la construccion Resolución del Tribunal Reunido el Tribunal designado a tal efecto, el doctorando / la doctoranda expone el tema de la su tesis doctoral titulada “Modelling and Structural Analysis of historical masonry systems including vaulted structure“ Acabada la lectura y después de dar respuesta a las cuestiones formuladas por los miembros titulares del tribunal, éste otorga la calificación: NO APTO APROBADO NOTABLE SOBRESALIENTE (Nombre, apellidos y firma) (Nombre, apellidos y firma) Presidente/a Secretario/a (Nombre, apellidos y firma) (Nombre, apellidos y firma) (Nombre, apellidos y firma) Vocal Vocal Vocal ______________________, _______ de __________________ de _______________ El resultado del escrutinio de los votos emitidos por los miembros titulares del tribunal, efectuado por la Escuela de Doctorado, a instancia de la Comisión de Doctorado de la UPC, otorga la MENCIÓN CUM LAUDE: SÍ NO (Nombre, apellidos y firma) (Nombre, apellidos y firma) Presidente de la Comisión Permanente de la Escuela de Secretario de la Comisión Permanente de la Escuela de Doctorado Doctorado Barcelona a _______ de ____________________ de __________ This page is left blank on purpose. Modelling and Structural Analysis of historical masonry systems including vaulted structure tesis doctoral realizada por: Yohei Endo dirigida por: Pere Roca i Fabregat Luca Pelà This page is left blank on purpose. ACKNOWLEDGEMENTS First of all, I would like to express the deepest appreciation to my supervisor Professor Pere Roca, who has shown the attitude and the substance of a genius: he continually and persuasively conveyed a spirit of adventure in regard to research, and an excitement in regard to teaching. Without his supervision and constant help this dissertation would not have been possible. I also would like to show my gratitude to my co-supervisor Dr Luca Pelà, who helped me out to deepen my understanding on numerical analysis and seismic assessment of historical structures. I would like to thank my committee members, Dr. Climent Molins, Dr. Miquel Llorens and Dr. Ignacio Lombillo, whose work demonstrated to me that concern for global affairs supported by an engagement in comparative literature and modern technology, should always transcend academia and provide a quest for our times. I thank Dr. Miquel Llorens for providing me valuable information on vaults of Hospital Sant Pau, as allowed us to conduct the study that comprises large part of the present research. In addition, I like to add a thank you to my colleague Ahmed Elyamani, who gave me tutorial of structural-analysis software, DIANA. I also would like to thank a past MSc SAHC student, Juan Arias who helped me for the study of one of vaults of Hospital Sant Pau. I would like to say thank you to a past master student from University of Padova, Alice de Conti, who carried out the study of San Marco church, as has provided useful information to us. I was grateful to attend NIKER project. It not only provided significant knowledge on the seismic assessment of a large-scale church and also made this thesis possible. I would like to show appreciation to the dance school, Seven Dance that has taught me the heart of Latin dance and that also has provided me strong moral support. In the end, I want to thank Nishihara Cultural Foundation, from bottom of my heart, for their financial support throughout this PhD research. i This page is left blank on purpose. ii ABSTRACT The conservation of historic structures has been given special attention due to their cultural, social and economic importance. However they often show considerable structural vulnerability and have been seriously damaged by natural disasters including earthquakes. An excessive loss of architectural heritage has occurred because of earthquakes. A safety assessment and restoration practice on historical structures has been tackled extensively by professionals including architects and engineers. However, structural assessment of historical buildings is a complex task. Complexity comes from insufficient understanding of the characteristic of historical materials, limited knowledge of the seismic response of historical structures and yet-unknown structural deterioration due to the past natural disasters. Today it is perceived that nonlinear FEM analysis permits detailed study of historical masonry structures. However, in some cases, its application poses difficulties. The difficulties derive from the definition of material properties, the definition of a complex geometry and the analysis procedures. The results depend on the material properties considerably. However, it is not easy to describe appropriately the behaviour of historical materials including masonry in the FEM analysis. The definition of a complex geometry is challenging although the discretisation of accurate geometry is crucial. As for the analysis procedure, one of the difficulties is observed in seismic assessment. FEM-based nonlinear dynamic analysis permits close observation of seismic response of a historical masonry structure but it requires excessive computational effort, for a large-scale structure in particular. On the other hand, pushover can be adopted more efficiently than nonlinear dynamic analysis but the obtained result can be less reliable. All these considerations indicate that the understanding of FEM approaches still needs to be deepened to adopt more accurately and at the same time efficiently for the analysis of historical structures. The present research discusses the applicability of existing nonlinear FEM approaches to the study of masonry historical structures. The FEM analysis is adopted to the analysis of real and complex structures including mixed steel and masonry vaulted systems belonging to the Hospital de Sant Pau in Barcelona and a large single-nave church damaged by the 2009 Abruzzo earthquake. As a final outcome of the research, the conclusions provided criteria and guidelines for the analysis of these types of structures under vertical loading and seismic forces. The achievement of the research will contribute to both engineers and researchers who are involved in the conservation of historical masonry structures especially by means of FEM analysis. iii This page is left blank on purpose. iv TABLE OF CONTENTS ACKNOWLEDGEMENTS....................................................................................................... i ABSTRACT ...........................................................................................................................iii TABLE OF CONTENTS ........................................................................................................ v TABLE OF FIGURES ........................................................................................................... ix LIST OF TABLES ............................................................................................................... xvii 1. INTRODUCTION AND OBJECTIVES ............................................................................ 1 1.1 Introduction ............................................................................................................... 1 1.2 Purpose of the thesis ................................................................................................ 2 1.2.1 General objective .............................................................................................. 2 1.2.2 Specific objectives ............................................................................................ 2 1.2.3 Summary .......................................................................................................... 3 2. STATE-OF-ART DISCUSSION ...................................................................................... 5 2.1 Masonry Mechanics .................................................................................................. 5 2.1.1 Mechanical properties ....................................................................................... 5 2.1.2 Structural behaviour ........................................................................................ 11 2.2 Typology and behaviour of masonry structural elements ......................................... 20 2.2.1 Typology of vertical structural elements .......................................................... 21 2.2.2 Damage and collapse mechanisms of vertical elements under seismic action ............................................................................................................... 26 2.2.3 Catalan Vaults ................................................................................................ 32 2.3 Structural Analysis techniques ................................................................................ 35 2.3.1 Limit analysis .................................................................................................
Load more

Recommended publications
  • Descriptive Memory
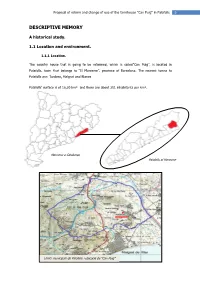
    Proposal of reform and change of use of the farmhouse "Can Puig" in Palafolls 9 DESCRIPTIVE MEMORY A historical study. 1.1 Location and environment. 1.1.1 Location. The country house that is going to be reformed, which is called"Can Puig", is located in Palafolls, town that belongs to “El Maresme”, province of Barcelona. The nearest towns to Palafolls are: Tordera, Malgrat and Blanes Palafolls’ surface is of 16,20 km² and there are about 251 inhabitants per km². Maresme a Catalunya Palafolls al Maresme Límits municipals de Palafolls i ubicació de “Can Puig” 10 Proposal for reform and change of use of the house "Can Puig" in Palafolls FIXED AND LOCATION OF SITE Name of the farmhouse Can Puig The Building Typology Isolated Region Maresme Municipality Palafolls Geographical height 16 m above the sea level Seismicity Low City Limits Tordera limited to the north, to the North for spite, east to Blanes (I) to the North West Santa Susana County boundaries Bounded to the north by Valles to the Eastern Mediterranean by sea, by Barcelona to the South and West-east forest. 1.1.2 Geography Relief: Palafolls is located to the northeastern border in the Maresme region (Barcelona) by Tordera limit of frontier with the region of La Selva and while the province of Girona. The Municipal term is 3.16 km ², and it’s 16 m above the sea level.. The first of December of 2006 population was 8,102 inhabitants. The most popular occupation in Palafoll is teh tourism industry. The central core is called Ferreries and two of the main neirhborhoods are Sta.
    [Show full text]
  • Art and Politics at the Neapolitan Court of Ferrante I, 1458-1494
    ABSTRACT Title of Dissertation: KING OF THE RENAISSANCE: ART AND POLITICS AT THE NEAPOLITAN COURT OF FERRANTE I, 1458-1494 Nicole Riesenberger, Doctor of Philosophy, 2016 Dissertation directed by: Professor Meredith J. Gill, Department of Art History and Archaeology In the second half of the fifteenth century, King Ferrante I of Naples (r. 1458-1494) dominated the political and cultural life of the Mediterranean world. His court was home to artists, writers, musicians, and ambassadors from England to Egypt and everywhere in between. Yet, despite its historical importance, Ferrante’s court has been neglected in the scholarship. This dissertation provides a long-overdue analysis of Ferrante’s artistic patronage and attempts to explicate the king’s specific role in the process of art production at the Neapolitan court, as well as the experiences of artists employed therein. By situating Ferrante and the material culture of his court within the broader discourse of Early Modern art history for the first time, my project broadens our understanding of the function of art in Early Modern Europe. I demonstrate that, contrary to traditional assumptions, King Ferrante was a sophisticated patron of the visual arts whose political circumstances and shifting alliances were the most influential factors contributing to his artistic patronage. Unlike his father, Alfonso the Magnanimous, whose court was dominated by artists and courtiers from Spain, France, and elsewhere, Ferrante differentiated himself as a truly Neapolitan king. Yet Ferrante’s court was by no means provincial. His residence, the Castel Nuovo in Naples, became the physical embodiment of his commercial and political network, revealing the accretion of local and foreign visual vocabularies that characterizes Neapolitan visual culture.
    [Show full text]
  • RAFAEL GUASTAVINO MORENO Inventiveness in 19Th Century Architecture by Jaume Rosell Colomina
    RAFAEL GUASTAVINO MORENO Inventiveness in 19th century architecture by Jaume Rosell Colomina This article was published in Catalan in pa. 494-522 by CAMARASA, Josep M.; ROCA, Antoni (dir.): Ciència i Tècnica als Països Catalans : una aproximació biogràfica (2v). Fundació Catalana per a la Recerca. Barcelona, 1995. The English version, revised by the author, was translated by Edward Krasny. An English version of this text was published in pp. 45-49 by TARRAGÓ, Salvador (editor): Guastavino Co. (1885-1962) : Catalogue of works in Catalonia and America. Col·legi d'Arquitectes de Catalunya. Barcelona, 2002. (ISBN 84-88258-65-8). Revised version, January 2010. Catalan and Spanish version in: https://upcommons.upc.edu/e-prints/browse?type=author&value=Rosell%2C+Jaume In memory of my father, Pere Rosell i Millach RAFAEL GUASTAVINO MORENO València, 1842 – Black Mountains, North Carolina, 1908 Key words: architecture, industrial architecture, cement, construction, cohesive construction, iron, brick, flat brick masonry, master builders, Modernisme, fire resistance, vaults. The contribution of Valencian Rafael Guastavino Moreno to Architecture was especially important in the technical area. He was the leading moderniser of an ancient building technique using flat brick masonry techniques, above all to erect vaults. Guastavino would later transfer these techniques from Catalonia to the United States of America, where he founded a family company that built, over two generations, more than one thousand buildings, many of them of great importance. These two accomplishments represent a notable contribution to contemporary Architecture: more so if we take into account a series of technological reflections and proposals that also constitute a contribution to the modernisation of construction, insofar as they entail an effort to understand the behaviour of and ways in which the new materials worked.
    [Show full text]
  • Architectural Renovation Using Traditional Technologies, Local Materials and Artisan’S Labor in Catalonia
    The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XLIV-M-1-2020, 2020 HERITAGE2020 (3DPast | RISK-Terra) International Conference, 9–12 September 2020, Valencia, Spain ARCHITECTURAL RENOVATION USING TRADITIONAL TECHNOLOGIES, LOCAL MATERIALS AND ARTISAN’S LABOR IN CATALONIA. O. Roselló 1, * 1 Architect Founder of www.bangolo.com and member co-founder of www.projectegreta.cat C.Pau Claris 154 Planta 4 Barcelona 08009 - [email protected] Commission II - WG II/8 KEY WORDS: Masia, Artisans, Vernacular, Architectural refurbish, Traditional technologies. ABSTRACT: The use of traditional techniques when restoring a masia is always the primary consideration in the preliminary phase of the project and during the site work. The virtues of traditional techniques compared to industrial production systems are described from multiple points of view: as a sustainable contemporary strategy, as generators of healthy spaces , as virtues of social and territorial scale, as a better formal contextualisation due to the limitations of pre-industrial materials. These are virtues that the industrial system has forgotten. The purpose of the Can Buch project (a masia in Northen Catalonia, Spain) was to restore the main house, some sheds and a barn, to enable rural ecotourism and to create a residence for the owner and future manager of the property. The promoter of the project intended to apply the values of permaculture. Maximising the use of Km0 materials from the start emphasised this intention. If we understand the traditional farmhouse as the site's resource map, applying this reality to the present work means recovering original representative principles. Currently, the project is in the last phase of works, but the results of applying this philosophy are already visible.
    [Show full text]
  • Catalan to English with Notes for English Speakers
    DACCO : The Open Source English-Catalan Dictionary - DACCO Catalan to English for English Speakers 2012-01 Catalan-English dictionary: 16540 entries, 24504 translations, 1592 examples 557 usage notes Attribution-ShareAlike 2.5 You are free: • to copy, distribute, display, and perform the work • to make derivative works • to make commercial use of the work Under the following conditions: Attribution. You must attribute the work in the manner specified by the author or licensor. Share Alike. If you alter, transform, or build upon this work, you may distribute the resulting work only under a license identical to this one. • For any reuse or distribution, you must make clear to others the license terms of this work. • Any of these conditions can be waived if you get permission from the copyright holder. Your fair use and other rights are in no way affected by the above. This is a human-readable summary of the Legal Code (full license). To view a copy of the full license, visit http://creativecommons.org/licenses/by-sa/2.5/ or send a letter to Creative Commons, 543 Howard Street, 5th Floor, San Francisco, California, 94105, USA. This PDF document was created using Prince. Prince. Prince is a powerful formatter that converts XML into PDF documents. Prince can read many XML formats, including XHTML and SVG. Prince formats documents according to style sheets written in CSS. Prince has been used to publish books, brochures, posters, letters and academic papers. Prince is also suitable for generating reports, invoices and other dynamic documents on demand. The DACCO team would like to thank Prince for the kind donation of a license to use their extremely powerful software which made this PDF possible.
    [Show full text]
  • Dictionary of Archaeological Terms Vocabulario De
    DICTIONARY OF DICTIONARY OF ARCHAEOLOGICAL ARCHAEOLOGICAL TERMS TERMS EnglishEnglish–French–Spanish // Spanish–EnglishFrench–English VOCABULARIO DICTIONNAIREDE CONCEPTOS DES ARQUEOLÓGICOSTERMES ARCHÉOLOGIQUES Inglés–Español / anglais–françaisEspañol–Inglés / français–anglais DomingoTinaig Carlos CLODORE-TISSOT SALAZAR GARCIA & Andrea MORENO MARTÍN © Domingo Carlos Salazar Garcia, Andrea Moreno Martín and Archaeopress 2011 Archaeopress Gordon House 276 Banbury Road Oxford OX2 7ED www.archaeopress.com ISBN 978-1-905739-47-9 Printed in England by 4edge, Hockley Other titles in the series now available: French/English – English/French Greek/English – English/Greek Forthcoming: Italian/English – English/Italian German/English – English/German Arabic/English – English/Arabic This dictionary is intended to be helpful in the reading of archaeological books and publications from the Palaeolithic to the Middle Ages, and in the writing of papers and articles in both English and Spanish. The aim of this work is to help, in particular, students and archaeologists in the field to find quickly a word relating to a specific period, a specific area or a research field, in a book easy to carry everywhere. But this dictionary is also intended for everyone fond of archaeology, from prehistory to the Middle Ages. Entries are classified according to alphabetical order. Basic grammar categories are denoted according to the abbreviations below: adj., adjective adv., adverb t.v., transitive verb i.v., intransitive verb n., noun pl.n., plural noun English–Spanish
    [Show full text]
  • Kunstgeschichte an Europas Peripherie
    KUNSTGESCHICHTE AN EUROPAS PERIPHERIE Der Palau de la Música Catalana – ein Konzertsaal im Barcelona der Jahrhundertwende unter metahistorisch-ideologiekritischer Perspektive Inaugural-Dissertation zur Erlangung der Doktorwürde der Philosophischen Fakultät der Rheinischen Friedrich-Wilhelms-Universität zu Bonn vorgelegt von Klaus Kehrlößer M. A. aus München Bonn 2003 INHALTSVERZEICHNIS 1VORWORT................................................................................................... III 2 EINFÜHRUNG ............................................................................................... 1 3 MODERNISMO............................................................................................ 10 4 DER BAU UND SEINE INNENAUSSTATTUNG ......................................... 20 5 METAHISTORISCHE ÜBERLEGUNGEN ZUR ARCHITEKTUR- GESCHICHTSSCHREIBUNG AM BEISPIEL DES PALAU UND DEM WERK DOMÈNECH I MONTANERS .......................................................... 43 METHODISCHE ÜBERLEGUNGEN..................................................................................... 43 MALEREI UND ARCHITEKTUR ........................................................................................... 47 DIE VERNACHLÄSSIGUNG SPANISCHER KUNST ........................................................... 49 DOMÈNECH UND GAUDÍ..................................................................................................... 62 POSTMODERNE..................................................................................................................
    [Show full text]
  • Antoni Gaudí 1 Antoni Gaudí
    Antoni Gaudí 1 Antoni Gaudí Antoni Gaudí Antoni Gaudí by Pau Audouard [1] [2] Born 25 June 1852Reus, Catalonia, Spain Died 10 June 1926 (aged 73)Barcelona, Catalonia, Spain Work Buildings Sagrada Família, Casa Milà, Casa Batlló Projects Parc Güell, Colònia Güell [3] Antoni Gaudí i Cornet (Catalan pronunciation: [ənˈtɔni ɣəwˈði]) (Riudoms or Reus, 25 June 1852 – Barcelona, 10 June 1926) was a Spanish Catalan architect and the best-known representative of Catalan Modernism. Gaudí's works are marked by a highly individual style and the vast majority of them are situated in the Catalan capital of Barcelona, including his magnum opus, the Sagrada Família. Much of Gaudí's work was marked by the four passions of his life: architecture, nature, religion and his love for Catalonia.[4] Gaudí meticulously studied every detail of his creations, integrating into his architecture a series of crafts, in which he himself was skilled, such as ceramics, stained glass, wrought ironwork forging and carpentry. He also introduced new techniques in the treatment of the materials, such as his famous trencadís, made of waste ceramic pieces. After a few years under the influence of neo-Gothic art, and certain oriental tendencies, Gaudí became part of the Catalan Modernista movement which was then at its peak, towards the end of the 19th century and the beginning of the 20th. Gaudí's work, however, transcended mainstream Modernisme, culminating in an organic style that was inspired by nature without losing the influence of the experiences gained earlier in his career. Rarely did Gaudí draw detailed plans of his works and instead preferred to create them as three-dimensional scale models, moulding all details as he was conceiving them in his mind.
    [Show full text]
  • Grado Arquitectura Técnica Y Edificacion
    GRADO ARQUITECTURA TÉCNICA Y EDIFICACION TRABAJO DE FIN DE GRADO FORMACION DE UNA EMPRESA CONSTRUCTORA Formación para el profesional, seguimiento de obra como empresa constructora ........................................................................................ Proyectista: Orestes Arana Pedrosa ........................................................................................................ Director: Manuel Agustiño .................................................................................. Convocatoria:Septiembre/Octubre 2019 Work monitoring as a construction company Orestes Arana Pedrosa 1.1 -INTRODUCTION The Degree‘s Project that I expose here is a construction practice that I have completed with my own company, PEDROSA & ARANA CONSTRUCCIONES SL, for which I have been working since January 2006. A construction firm with a familiar background and a tradition in the bricklaying profession, even tough, in this case it was a professional adventure forced by circumstances. A path from salaried, freelance, SCP, and Limited Company. Nowadays, I work in a unipersonal Limited Company known as O. Arana Construcciones. The Project has three parts: PART 1. THE PROFESSION OF CONSTRUCTION AND ITS RELATED TRAINING The first point is the process or best remediation to improve the work‘s quality in constructions; the training of professionals. In our country, there is a serious problem with professionality in construction. Many years ago, this stopped being an attractive sector for different circumstances that we will closely analyse; we will revise different training alternatives for professionals, novices and experts under the point of view of a professional trainer. There will be an introduction of how inquisitiveness and luck of being able to give theoretical and practical lessons in the ―Escola Gaudí de Barcelona‖, nowadays known as ―Centro Formativo de la Fundación Laboral de la Construcción‖. In the space dedicated to the profession, singular constructive details will be exposed as well.
    [Show full text]
  • Catenary Vaults: a Solution to Low-Cost Housing in South Africa
    Catenary Vaults: A solution to low-cost housing in South Africa Ivanka Bulovic A research report submitted to the Faculty of Engineering and the Built Environment, University of the Witwatersrand, Johannesburg, in partial fulfilment of the requirements for the degree of Master of Science in Engineering. Johannesburg 2014 The financial assistance of the National Research Foundation (N R F) towards this research is hereby acknowledged. Opinions expressed and conclusions arrived at, are those of the author and are not necessarily to be attributed to the NRF. Table of Contents Table of Contents ................................................................................................................................. 1 Declaration ............................................................................................................................................ 5 Abstract .................................................................................................................................................. 6 Acknowledgements .............................................................................................................................. 7 List of Figures ....................................................................................................................................... 8 List of Tables ....................................................................................................................................... 13 List of Symbols ..................................................................................................................................
    [Show full text]
  • Neupane, Babita, Ms. December 2020 Architecture
    NEUPANE, BABITA, MS. DECEMBER 2020 ARCHITECTURE EXPLORING FORMS OF MASONRY VAULTS BUILT WITHOUT CENTERING Thesis Advisor: Dr. Rui Liu Inspired by the historical construction technique and contemporary form-finding methods, as well as practices in designing and constructing masonry vaults, the thesis explores different forms that can be built without centering during construction. This thesis examines the literature associated with the geometries, construction techniques and methods used to generate masonry arches, vaults, and domes without centering or with minimum supports. The main idea lies on the self-supporting courses where each masonry unit has its own equilibrium condition. Based on the principles of equilibrium, this research develops algorithms for two cases: when bricks are not bonded with mortar and are bonded with mortar. The algorithms to generate an arch when subjected to additional vertical loads for both cases have also been investigated. Moreover, using the Python component in Grasshopper, a tool is developed using the proposed algorithms in this thesis. The tool is used for parametric designs to create new forms of masonry vaults which could be built without centering. EXPLORING FORMS OF MASONRY VAULTS BUILT WITHOUT CENTERING A thesis submitted to Kent State University in partial fulfillment of the requirements for the Degree of Master of Science in Architecture and Environmental Design by Babita Neupane December 2020 @Copyright All rights reserved Except for previously published materials Thesis written by Babita Neupane B.Arch., Tribhuvan University, Nepal, 2015 M.S. in Architecture and Environmental Design, December 2020 Approved by Rui Liu, Ph.D., PE , Advisor Reid Coffman, MLA, Ph.D.
    [Show full text]
  • This Is Catalonia
    this is CAtALONiA A Guide to Architectural Heritage :BibliotecadeCatalunya-DadesCIP Pladevall i Font, Antoni, 1934- ThisisCatalonia:aguidetothearchitecturalheritage ISBN9788439386810 I.NavarroiCossio,Antoni,1939-II.López,Mercè LópezFort),ed.III.Catalunya.GeneralitatIV.Títol) Edificishistòrics–Catalunya–Guies 2. Monuments .1 Catalunya–Guies– (036)(467.1)721 Authors AntoniPladevalliFont AntoniNavarroiCossío Photographs ,DGPC:DirectorateGeneralforCulturalHeritage/JordiContijoch,JosepGiribet,JordiGumí ,.LourdesJansana,MercèLópez,MontserratManent,BobMasters,NortoMéndez,PaisajesE JordiPlay,MartaPrat,AlbertSierra MHC:TheMuseumofHistoryofCatalonia/PepBotey,PepoSegura MNAT:TheNationalArchaeologicalMuseumofTarragona;MAC:TheArchaeologicalMuseumofCatalonia ARXIUMNACTEC:TheNationalMuseumofScienceandTechnologyofCatalonia/TeresaLlordés MEMGA:TheEthnologicalMuseumoftheMontseny/JosepCamps CRBM:CentrefortheRestorationofCulturalWorks/CarlesAymerich .TheLaPaneraArtCentre/JordiV.Pou;PalauRobert/JosepMoragues,ACNAS.L ,CE09:WinnersoftheFlickrpatrimoni.gencatcompetition.Summer2009/agueda_galimany,amnares ,andrEsA,MariaDolorsAñon,IsidreCanela,FrancescCarreras,MontseCrivillers,JordiChueca ,AlbertCodina,JaumeGassol,ManelGrau,guspiraalsnúvols,CarlesIlla,jparellada,EnricLópez ,FerranLavall,llumimirada,mami13,ManelMarqués,MontseMarse,meydema,msegarra_mso,LaNoguera
    [Show full text]