Assessment of Density Functional Methods with Correct Asymptotic
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ereztech LLC P3553 Safety Data Sheet
EREZTECH LLC 11555 Medlock Bridge Road, Suite 100, Johns Creek, GA 30097, USA T: +1.888.658.1221 F: 1.678.619.2020 E: [email protected] W: https://ereztech.com Section 1. Identification Product Name: Phosphorus trifluoride Product Type: Gas CAS Number: 7783-55-3 Product Number: P3553 Product Manufacturer: Ereztech LLC 11555 Medlock Bridge Road, Suite 100 Johns Creek, GA 30097 Product Information: (888) 658-1221 In Case of an Emergency: CHEMTREC: 1-800-424-9300 (USA); +1 703-527-3887 (International); CCN836180 *** Contact manufacturer for all non-emergency calls. Section 2. Hazards Identification Appearance/Odor: Colorless, odorless gas. Classification: ACUTE TOXICITY, ORAL - Category 4, H302 ACUTE TOXICITY, DERMAL - Category 4, H312 SKIN CORROSION/IRRITATION - Category 1B, H314 SERIOUS EYE DAMAGE/EYE IRRITATION - Category 2, H318 ACUTE TOXICITY, INHALATION - Category 1, H330 SPECIFIC TARGET ORGAN TOXICITY, SINGLE EXPOSURE; RESPIRATORY TRACT IRRITATION – Category 3, H335 GHS Label Elements Hazard Pictograms: Signal Word: DANGER Hazard Statements: H302: Harmful if swallowed. H312: Harmful in contact with skin. H314: Causes severe skin burns and eye damage. H318: Causes serious eye damage. H330: Fatal if inhaled. H335: May cause respiratory irritation. Ereztech P3553 Page 1 of 13 Revision: 1.00 Date of Issue: 11/27/2020 Phosphorus trifluoride Safety Data Sheet Section 2. Hazards Identification Precautionary Statements Prevention: P260: Do not breathe fumes/gases/mists/vapors/sprays. P264: Wash skin thoroughly after handling. P270: Do not eat, drink or smoke when using this product. P271: Use only outdoors or in a well-ventilated area. P280: Wear protective gloves/ protective clothing/ eye protection/ face protection. -

(12) Patent Application Publication (10) Pub. No.: US 2005/0044778A1 Orr (43) Pub
US 20050044778A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2005/0044778A1 Orr (43) Pub. Date: Mar. 3, 2005 (54) FUEL COMPOSITIONS EMPLOYING Publication Classification CATALYST COMBUSTION STRUCTURE (51) Int. CI.' ........ C10L 1/28; C1OL 1/24; C1OL 1/18; (76) Inventor: William C. Orr, Denver, CO (US) C1OL 1/12; C1OL 1/26 Correspondence Address: (52) U.S. Cl. ................. 44/320; 44/435; 44/378; 44/388; HOGAN & HARTSON LLP 44/385; 44/444; 44/443 ONE TABOR CENTER, SUITE 1500 1200 SEVENTEENTH ST DENVER, CO 80202 (US) (57) ABSTRACT (21) Appl. No.: 10/722,127 Metallic vapor phase fuel compositions relating to a broad (22) Filed: Nov. 24, 2003 Spectrum of pollution reducing, improved combustion per Related U.S. Application Data formance, and enhanced Stability fuel compositions for use in jet, aviation, turbine, diesel, gasoline, and other combus (63) Continuation-in-part of application No. 08/986,891, tion applications include co-combustion agents preferably filed on Dec. 8, 1997, now Pat. No. 6,652,608. including trimethoxymethylsilane. Patent Application Publication Mar. 3, 2005 US 2005/0044778A1 FIGURE 1 CALCULATING BUNSEN BURNER LAMINAR FLAME VELOCITY (LFV) OR BURNING VELOCITY (BV) CONVENTIONAL FLAME LUMINOUS FLAME Method For Calculating Bunsen Burner Laminar Flame Velocity (LHV) or Burning Velocity Requires Inside Laminar Cone Angle (0) and The Gas Velocity (Vg). LFV = A, SIN 2 x VG US 2005/0044778A1 Mar. 3, 2005 FUEL COMPOSITIONS EMPLOYING CATALYST Chart of Elements (CAS version), and mixture, wherein said COMBUSTION STRUCTURE element or derivative compound, is combustible, and option 0001) The present invention is a CIP of my U.S. -

Chemical Chemical Hazard and Compatibility Information
Chemical Chemical Hazard and Compatibility Information Acetic Acid HAZARDS & STORAGE: Corrosive and combustible liquid. Serious health hazard. Reacts with oxidizing and alkali materials. Keep above freezing point (62 degrees F) to avoid rupture of carboys and glass containers.. INCOMPATIBILITIES: 2-amino-ethanol, Acetaldehyde, Acetic anhydride, Acids, Alcohol, Amines, 2-Amino-ethanol, Ammonia, Ammonium nitrate, 5-Azidotetrazole, Bases, Bromine pentafluoride, Caustics (strong), Chlorosulfonic acid, Chromic Acid, Chromium trioxide, Chlorine trifluoride, Ethylene imine, Ethylene glycol, Ethylene diamine, Hydrogen cyanide, Hydrogen peroxide, Hydrogen sulfide, Hydroxyl compounds, Ketones, Nitric Acid, Oleum, Oxidizers (strong), P(OCN)3, Perchloric acid, Permanganates, Peroxides, Phenols, Phosphorus isocyanate, Phosphorus trichloride, Potassium hydroxide, Potassium permanganate, Potassium-tert-butoxide, Sodium hydroxide, Sodium peroxide, Sulfuric acid, n-Xylene. Acetone HAZARDS & STORAGE: Store in a cool, dry, well ventilated place. INCOMPATIBILITIES: Acids, Bromine trifluoride, Bromine, Bromoform, Carbon, Chloroform, Chromium oxide, Chromium trioxide, Chromyl chloride, Dioxygen difluoride, Fluorine oxide, Hydrogen peroxide, 2-Methyl-1,2-butadiene, NaOBr, Nitric acid, Nitrosyl chloride, Nitrosyl perchlorate, Nitryl perchlorate, NOCl, Oxidizing materials, Permonosulfuric acid, Peroxomonosulfuric acid, Potassium-tert-butoxide, Sulfur dichloride, Sulfuric acid, thio-Diglycol, Thiotrithiazyl perchlorate, Trichloromelamine, 2,4,6-Trichloro-1,3,5-triazine -
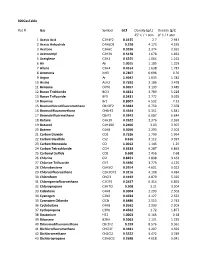
Gas Conversion Factor for 300 Series
300GasTable Rec # Gas Symbol GCF Density (g/L) Density (g/L) 25° C / 1 atm 0° C / 1 atm 1 Acetic Acid C2H4F2 0.4155 2.7 2.947 2 Acetic Anhydride C4H6O3 0.258 4.173 4.555 3 Acetone C3H6O 0.3556 2.374 2.591 4 Acetonitryl C2H3N 0.5178 1.678 1.832 5 Acetylene C2H2 0.6255 1.064 1.162 6 Air Air 1.0015 1.185 1.293 7 Allene C3H4 0.4514 1.638 1.787 8 Ammonia NH3 0.7807 0.696 0.76 9 Argon Ar 1.4047 1.633 1.782 10 Arsine AsH3 0.7592 3.186 3.478 11 Benzene C6H6 0.3057 3.193 3.485 12 Boron Trichloride BCl3 0.4421 4.789 5.228 13 Boron Triflouride BF3 0.5431 2.772 3.025 14 Bromine Br2 0.8007 6.532 7.13 15 Bromochlorodifluoromethane CBrClF2 0.3684 6.759 7.378 16 Bromodifluoromethane CHBrF2 0.4644 5.351 5.841 17 Bromotrifluormethane CBrF3 0.3943 6.087 6.644 18 Butane C4H10 0.2622 2.376 2.593 19 Butanol C4H10O 0.2406 3.03 3.307 20 Butene C4H8 0.3056 2.293 2.503 21 Carbon Dioxide CO2 0.7526 1.799 1.964 22 Carbon Disulfide CS2 0.616 3.112 3.397 23 Carbon Monoxide CO 1.0012 1.145 1.25 24 Carbon Tetrachloride CCl4 0.3333 6.287 6.863 25 Carbonyl Sulfide COS 0.668 2.456 2.68 26 Chlorine Cl2 0.8451 2.898 3.163 27 Chlorine Trifluoride ClF3 0.4496 3.779 4.125 28 Chlorobenzene C6H5Cl 0.2614 4.601 5.022 29 Chlorodifluoroethane C2H3ClF2 0.3216 4.108 4.484 30 Chloroform CHCl3 0.4192 4.879 5.326 31 Chloropentafluoroethane C2ClF5 0.2437 6.314 6.892 32 Chloropropane C3H7Cl 0.308 3.21 3.504 33 Cisbutene C4H8 0.3004 2.293 2.503 34 Cyanogen C2N2 0.4924 2.127 2.322 35 Cyanogen Chloride ClCN 0.6486 2.513 2.743 36 Cyclobutane C4H8 0.3562 2.293 2.503 37 Cyclopropane C3H6 0.4562 -

Phosphorus Compounds
Phosphorus Compounds Table of Contents How to Cite This Article Phosphorus Compounds, Compounds of phosphorus play vital roles in the metabolism of both plants and animals. The energy "currency" of all living things, adenosine triphosphate (ATP), is probably the best-known organic phosphorus compound, but others are constituents of nervous tissue, cell membranes, and other tissues, as well as of many coenzymes. Phosphates also are key components of DNA and RNA, which carry genetic information in all organisms. Many phosphorus compounds are used in industrial processes. Most phosphorus compounds exhibit covalent properties. Ionic compounds, such as sodium 3− phosphide (Na3P), are few because the formation of P ions from P atoms requires a considerable amount of energy. Similarly, P5+ ions do not exist due to the very high ionization energies involved. The chemistry of phosphorus in forming compounds generally is similar to that of carbon and nitrogen. Phosphine Phosphine, PH3, is a very toxic gas with a garliclike odor. When inhaled it can cause restlessness, followed by tremors, fatigue, drowsiness, nausea, and often severe gastric pain. In most cases recovery occurs without aftereffects, but some cases may result in coma or convulsions and even death. Phosphine can be readily prepared by reacting calcium or aluminum phosphide with dilute acid. On a large scale, PH3 is obtained by action of sodium hydroxide on white phosphorus; − hypophosphite (H2PO 2) is also formed. Pure phosphine is not spontaneously flammable. It is readily oxidized by air when ignited, and explosive mixtures may be formed. Phosphine is sparingly soluble in water, and an aqueous solution of PH3 is neither acidic nor basic. -

Chemical Names and CAS Numbers Final
Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number C3H8O 1‐propanol C4H7BrO2 2‐bromobutyric acid 80‐58‐0 GeH3COOH 2‐germaacetic acid C4H10 2‐methylpropane 75‐28‐5 C3H8O 2‐propanol 67‐63‐0 C6H10O3 4‐acetylbutyric acid 448671 C4H7BrO2 4‐bromobutyric acid 2623‐87‐2 CH3CHO acetaldehyde CH3CONH2 acetamide C8H9NO2 acetaminophen 103‐90‐2 − C2H3O2 acetate ion − CH3COO acetate ion C2H4O2 acetic acid 64‐19‐7 CH3COOH acetic acid (CH3)2CO acetone CH3COCl acetyl chloride C2H2 acetylene 74‐86‐2 HCCH acetylene C9H8O4 acetylsalicylic acid 50‐78‐2 H2C(CH)CN acrylonitrile C3H7NO2 Ala C3H7NO2 alanine 56‐41‐7 NaAlSi3O3 albite AlSb aluminium antimonide 25152‐52‐7 AlAs aluminium arsenide 22831‐42‐1 AlBO2 aluminium borate 61279‐70‐7 AlBO aluminium boron oxide 12041‐48‐4 AlBr3 aluminium bromide 7727‐15‐3 AlBr3•6H2O aluminium bromide hexahydrate 2149397 AlCl4Cs aluminium caesium tetrachloride 17992‐03‐9 AlCl3 aluminium chloride (anhydrous) 7446‐70‐0 AlCl3•6H2O aluminium chloride hexahydrate 7784‐13‐6 AlClO aluminium chloride oxide 13596‐11‐7 AlB2 aluminium diboride 12041‐50‐8 AlF2 aluminium difluoride 13569‐23‐8 AlF2O aluminium difluoride oxide 38344‐66‐0 AlB12 aluminium dodecaboride 12041‐54‐2 Al2F6 aluminium fluoride 17949‐86‐9 AlF3 aluminium fluoride 7784‐18‐1 Al(CHO2)3 aluminium formate 7360‐53‐4 1 of 75 Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number Al(OH)3 aluminium hydroxide 21645‐51‐2 Al2I6 aluminium iodide 18898‐35‐6 AlI3 aluminium iodide 7784‐23‐8 AlBr aluminium monobromide 22359‐97‐3 AlCl aluminium monochloride -
Download (8MB)
Harvey, David Allan (1984) The synthesis and oxidation of some cyclophosphazanes. PhD thesis http://theses.gla.ac.uk/4036/ Copyright and moral rights for this thesis are retained by the author A copy can be downloaded for personal non-commercial research or study, without prior permission or charge This thesis cannot be reproduced or quoted extensively from without first obtaining permission in writing from the Author The content must not be changed in any way or sold commercially in any format or medium without the formal permission of the Author When referring to this work, full bibliographic details including the author, title, awarding institution and date of the thesis must be given Glasgow Theses Service http://theses.gla.ac.uk/ [email protected] THE SYNTHESIS AND OXIDATION OF SOME CYCLOPHOSPHAZANES. A thesis submitted to the University of Glasgow in fulfilment of the requirements for the degree of DOCTOR OF PHILOSOPHY by David Allan Harvey, B. Sc. Department of Chemistry, University of Glasgow, Glasgow G12 8QQ To My Mother and Father. Acknowledgements I wish to thank my supervisor, Dr R. Keat for his support, advice and encouragement throughout the course of this work. I would also like to thank my colleagues in the Chemistry Department for their assistance. In particular, is special thanks due to Dr. D. S. Rycroft for his help with 31P n. m. r. spectroscopy. Thanks is also due to Mrs. M. Ewart, who assisted with the typing and preparation of this thesis. Finally, I would like to thank the University of Glasgow for their financial support of this research. -

PROHIBITED ITEMS Prohibited Items Are Items the Laboratory Is Prohibited from Purchasing with Government Funds Without Special Approval
PROHIBITED ITEMS Prohibited Items are items the Laboratory is prohibited from purchasing with Government funds without special approval. Prohibited Items are not to be purchased using PCard, eBuy, or B2B System Contracts. These items may be purchased on regular purchase orders only after approval (which may include DOE approval) is obtained. Item Description Reason ANY ITEM THAT IS NON-ESSENTIAL FOR LABORATORY BUSINESS Not allowed per SP 31.3 Advertising to promote the University or Laboratory Unallowable per FAR 31 and SP 31.3 Alcoholic beverages Unallowable per FAR 31 and SP 31.3 Coffee pots and machines, electric water kettles Not allowed Contributions and donations Unallowable per FAR 31 and SP 31.3 Decorative Items (e.g., framing for personal use, plants) Not allowed Eavesdropping and wiretapping equipment Unallowable per DEAR 908.7114 Entertainment expense Unallowable per FAR 31 and SP 31.3 Fines or penalties resulting from violations of Federal, state, local, or foreign laws and regulations Unallowable per FAR 31 Food and supplies for employees or routine meetings; including coffee and coffee accessories RPM: Events and Meals – Planning and Reporting Insurance (including value declarations) Unallowable per FAR 31 Hospitals and related medical services Not allowed Housing Not allowed License fees (except software license, without terms and conditions) DOE approval required. SP 27.1 Lobbying costs Unallowable per FAR 31 Luxury Items (above what is absolutely necessary to accomplish the Lab's mission) Not allowed per SP 31.3 Memberships in social, dining, or country clubs Unallowable per FAR 31 Personal property (for use in an office/cubicle (non-communal area); e.g. -

Topics in Phosphorus-Flij Orine Chemistry
TOPICS IN PHOSPHORUS-FLIJ ORINE CHEMISTRY ProQuest Number: 11011943 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a com plete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest ProQuest 11011943 Published by ProQuest LLC(2018). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States C ode Microform Edition © ProQuest LLC. ProQuest LLC. 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106- 1346 THESIS submitted to the UNIVERSITY OF GLASGOW in fulfilment of the requirements for the DEGREE OF DOCTOR OF PHILOSOPHY *>y JOHN SIDNEY HARMAN B.A. Department of Chemistry, University of Glasgow, GLASGOW August 1970* DEDICATED TO THE PARENTS THAT HAVE TOLERATED ME. “Everything*s got a moral, if only you can find it.11 - Lewis Carroll ACKNOWLEDGEMENTS I am especially grateful to Professor D.W.A. Sharp for his encouragement and advice during the course of this work. My thanks is also expressed to my postgraduate colleagues both past and present, for many informative discussions. I am indebted to Dr. R. Keat for the supply of some starting materials and the prior communication of some of his results. I should also like to acknowledge the assistance of Mary McCartney in obtaining some results as part of her ij-th year project. -

THE CHEMISTRY of SOME TRIPLUOROMETHYL-PHOSPHINES . by MIRZA ARSHAD ALI BEG B..Sc
THE CHEMISTRY of SOME TRIPLUOROMETHYL-PHOSPHINES . by MIRZA ARSHAD ALI BEG B..Sc.(Hons.)f M.Sc. (Karachi), 1955» A thesis submitted in partial fulfilment of the requirements for the degree of DOCTOR OF PHILOSOPHY in the Department of Chemistry. We accept this thesis as conforming to the required standard© THE UNIVERSITY OP BRITISH COLUMBIA June, 1961. In presenting this thesis in partial fulfilment of the requirements for an advanced degree at the University of British Columbia, I agree that the Library shall make it freely available for reference and study. I further agree that permission for extensive copying of this thesis for scholarly purposes may be granted by the Head of my Department or by his representatives. It is understood that copying or publication' of this thesis for financial gain shall not be allowed'without my written permission. Department of ^^R^+^C&&^ The University of British Columbia, Vancouver 8, Canada. Date Af*Ql.tfc% /9£f GRADUATE STUDIES Wqp Pntuersttg of ^rtttsii Columbia Field of Study: Inorganic Chemistry Topics in Inorganic Chemistry H. C. Clark H. G. Heal FACULTY OF GRADUATE STUDIES Topics in Organic Chemistry L. D. Hayward D. E. McGreer A. Rosenthal R. Stewart Radiochemistry D. R. Wiles Seminar in Chemistry : R. Stewart Related Studies: PROGRAMME OF THE . Atomic Physics K. L. Erdman ! FINAL ORAL EXAMINATION Geophysics '. J. A. Jacobs Structure of Metals II V. Griffiths j FOR THE DEGREE OF E. Teghtsoonian DOCTOR OF PHILOSOPHY of M. ARSHAD A. BEG B.Sc. (Hons), M.Sc. (Karachi) PUBLICATIONS FRIDAY, JULY 28th, 1961 at 2:30 p.m. -
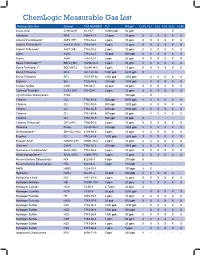
Chemlogic Measurable Gas List
ChemLogic Measurable Gas List Measureable Gas Symbol CAS NUMBER TLV Range* CLPx CL1 CL2 CL4 CL8 CL96 Acetic Acid CH3CO2H 64-19-7 10000 ppb 50 ppb - - - - X - Ammonia NH3 7664-41-7 25 ppm 75 ppm X X X X X X Arsenic Pentafluoride^ AsF5 (HF) 7784-36-3 2 ppm 10 ppm X X X X X X Arsenic Trichloride^^ AsHCl3 (HCl) 7784-34-1 5 ppm 15 ppm X X X X X X Arsenic Trifluoride^ AsF3 (HF) 7784-35-2 2 ppm 10 ppm X X X X X X Arsine AsH3 7784-42-1 50 ppb 500 ppb X X X X X X Arsine AsH3 7784-42-1 5 ppb 50 ppb X X X X X X Boron Tribromide^^^ BBr3 (HBr) 10294-33-4 3 ppm 20 ppm X X X X X X Boron Trichloride^^ BCl3 (HCl) 10294-34-5 5 ppm 15 ppm X X X X X X Boron Trifluoride BF3 7637-07-02 1000 ppb 5000 ppb X - - - - - Boron Trifluoride BF3 7637-07-02 1000 ppb 3200 ppb - X X X X X Bromine Br2 7726-95-6 100 ppb 1000 ppb - X X X X X Carbon Sulfide COS 463-58-1 20 ppm 20 ppm X X X X X X Carbonyl Fluoride^ COF2 (HF) 353-50-4 2 ppm 10 ppm X X X X X X Cyclohexane Diisocyanate CHDI - 100 ppb - X - - - - Chlorine Cl2 7782-50-5 500 ppb 5000 ppb X X X X X X Chlorine Cl2 7782-50-5 500 ppb 3200 ppb - X X X X X Chlorine Cl2 7782-50-5 500 ppb 2000 ppb X X X X X X Chlorine Cl2 7782-50-5 500 ppb 30 ppb - X X X X X Chlorine Cl2 7782-50-5 500 ppb 20 ppb X - - - - - Chlorine Trifluoride^ ClF3 (HF) 7790-91-2 2 ppm 10 ppm X X X X X X Diborane B2H6 19287-45-7 100 ppb 1000 ppb X X X X X X Dichlorosilane^^ SiH3Cl2 (HCl) 4109-96-0 5 ppm 15 ppm X X X X X X Fluorine F2 7782-41-4 1000 ppb 3200 ppb X X X X X X Fluosilic Acid^ H2SiF6 (HF) 16961-83-4 2 ppm 10 ppm X X X X X X Germane GeH4 7782-65-2 -

New York City Department of Environmental Protection Community Right-To-Know: List of Hazardous Substances
New York City Department of Environmental Protection Community Right-to-Know: List of Hazardous Substances Updated: 12/2015 Definitions SARA = The federal Superfund Amendments and Reauthorization Act (enacted in 1986). Title III of SARA, known as the Emergency Planning and Community Right-to-Act, sets requirements for hazardous chemicals, improves the public’s access to information on chemical hazards in their community, and establishes reporting responsibilities for facilities that store, use, and/or release hazardous chemicals. RQ = Reportable Quantity. An amount entered in this column indicates the substance may be reportable under §304 of SARA Title III. Amount is in pounds, a "K" represents 1,000 pounds. An asterisk following the Reporting Quantity (i.e. 5000*) will indicate that reporting of releases is not required if the diameter of the pieces of the solid metal released is equal to or exceeds 100 micrometers (0.004 inches). TPQ = Threshold Planning Quantity. An amount entered in this column reads in pounds and indicates the substance is an Extremely Hazardous Substance (EHS), and may require reporting under sections 302, 304 & 312 of SARA Title III. A TPQ with a slash (/) indicates a "split" TPQ. The number to the left of the slash is the substance's TPQ only if the substance is present in the form of a fine powder (particle size less than 100 microns), molten or in solution, or reacts with water (NFPA rating = 2, 3 or 4). The TPQ is 10,000 lb if the substance is present in other forms. A star (*) in the 313 column= The substance is reportable under §313 of SARA Title III.