DOCSLIB.ORG

A Fluorescent Speckle Microscopy Study

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Fluorescent Speckle Microscopy Study Research Collection Doctoral Thesis High-resolution analysis of F-actin meshwork kinetics and kinematics using computational Fluorescent Speckle Microscopy Author(s): Ponti, Aaron Christian Publication Date: 2003 Permanent Link: https://doi.org/10.3929/ethz-a-004650398 Rights / License: In Copyright - Non-Commercial Use Permitted This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use. ETH Library DISS. ETH NO. 15286 High-Resolution Analysis of F-Actin Meshwork Kinetics and Kinematics using Computational Fluorescent Speckle Microscopy A dissertation submitted to the SWISS FEDERAL INSTITUTE OF TECHNOLOGY ZURICH For the degree of Doctor of Sciences Presented by Aaron Christian Ponti Dipl. Natw. ETHZ Born 30.10.1975 Citizen of Breganzona (TI) Accepted on the recommendation of Prof. Dr. Gaudenz Danuser, examiner Prof. Dr. Jonathon Howard, co-examiner Prof. Dr. Yves Barral, co-examiner 2003 2 Table of contents Table of contents TABLE OF CONTENTS...................................................................................................................................... 3 SUMMARY ........................................................................................................................................................... 7 SOMMARIO ......................................................................................................................................................... 9 1 INTRODUCTION .......................................................................................................................................... 13 1.1 FUNDAMENTS OF CELL MOTILITY ............................................................................................................... 14 1.1.1 Cell locomotion ..................................................................................................................................... 14 1.1.2 Actin ...................................................................................................................................................... 15 1.1.3 Protrusion is driven by actin-polymerization........................................................................................ 16 1.1.4 The role of signaling on the spatial control of actin assembly.............................................................. 18 1.1.5 Stabilization of the actin meshwork....................................................................................................... 20 1.1.6 Cell body translocation ......................................................................................................................... 20 1.2 FLUORESCENT SPECKLE MICROSCOPY ........................................................................................................ 22 1.2.1 FSM origins and fields of application................................................................................................... 22 1.2.2 Quantitative FSM.................................................................................................................................. 25 1.3 OUTLINE OF THE THESIS ............................................................................................................................. 25 2 COMPUTATIONAL ANALYSIS OF F-ACTIN TURNOVER IN CORTICAL ACIN MESHWORKS USING FLUORESCENT SPECKLE MICROSCOPY .............................................................................. 27 2.1 INTRODUCTION........................................................................................................................................... 28 2.2 MATERIALS AND METHODS ........................................................................................................................ 29 2.2.1 Software development ........................................................................................................................... 29 2.2.2 Synthesis of FSM movies using Monte Carlo simulations of dynamic F-actin meshworks................... 29 2.2.3 Cell Manipulations................................................................................................................................ 31 2.2.4 Time-lapse Spinning Disk Confocal FSM ............................................................................................. 32 2.2.5 Characterization of image noise ........................................................................................................... 32 2.2.5.1 Titration experiments........................................................................................................................................ 32 2.2.5.2 Calibration of a noise model............................................................................................................................. 33 2.3 ALGORITHM ............................................................................................................................................... 33 2.3.1 Noise reduction and local maximum selection...................................................................................... 33 2.3.2 Statistical selection of speckles ............................................................................................................. 36 2.3.3 Micro-movement tracking ..................................................................................................................... 40 2.3.4 Removal of time gaps in speckle trajectories ........................................................................................ 41 2.3.5 Classification of birth and death events................................................................................................ 42 2.3.6 Kinetic analysis of birth and death events and accumulation of actin turnover maps .......................... 45 2.4 RESULTS..................................................................................................................................................... 48 2.4.1 Verification of the algorithm on synthetic data..................................................................................... 48 2.4.2 FSM analysis of cortical actin meshworks reveals cyclic polymer turnover ........................................ 49 3 Table of contents 2.4.3 Latrunculin A perfusion induces a spreading of the cycle frequencies ................................................. 53 2.5 DISCUSSION................................................................................................................................................ 54 2.5.1 FSM analysis relies on a statistical separation of significant events.................................................... 54 2.5.2 The effect of bleaching on FSM analysis is minimal and can be eliminated completely by an appropriate correction scheme........................................................................................................................ 56 2.5.3 The effect of focus changes.................................................................................................................... 59 2.5.4 Local meshwork contractions are most likely to result in ghost speckles which are excluded from the analysis............................................................................................................................................................ 61 2.6 ACKNOWLEDGEMENTS ............................................................................................................................... 63 3 RECOVERY, VISUALIZATION, AND ANALYSIS OF ACTIN AND TUBULIN POLYMER FLOW IN LIVE CELLS: A FLUORESCENT SPECKLE MICROSCOPY STUDY ......................................... 65 3.1 INTRODUCTION........................................................................................................................................... 66 3.1.1 FSM of filamentous actin flow at the leading edge of migrating cells .................................................. 67 3.1.2 FSM of poleward microtubule flux in mitotic spindles.......................................................................... 68 3.1.3 Scope of the paper................................................................................................................................. 69 3.2 MATERIALS AND METHODS ........................................................................................................................ 70 3.2.1 FSM of actin in migrating newt lung epithelial cells ............................................................................70 3.2.2 FSM of mitotic spindle in Xenopus eggs extracts.................................................................................. 70 3.3 ALGORITHM ............................................................................................................................................... 71 3.3.1 Signal preconditioning.......................................................................................................................... 71 3.3.2 Particle generation................................................................................................................................ 71 3.3.3 Particle selection................................................................................................................................... 71 3.3.4 Generation of candidate matches.......................................................................................................... 72 3.3.5 Selection of matches.............................................................................................................................
Load more

Recommended publications
  • BSCB Newsletter 2017D
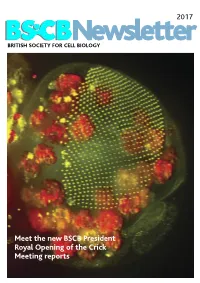
    2017 BSCB Newsletter BRITISH SOCIETY FOR CELL BIOLOGY Meet the new BSCB President Royal Opening of the Crick Meeting reports 2017 CONTENTS BSCB Newsletter News 2 Book reviews 7 Features 8 Meeting Reports 24 Summer students 30 Society Business 33 Editorial Welcome to the 2017 BSCB newsletter. After several meeting hosted several well received events for our Front cover: years of excellent service, Kate Nobes has stepped PhD and Postdoc members, which we discuss on The head of a Drosophila pupa. The developing down and handed the reins over to me. I’ve enjoyed page 5. Our PhD and Postdoc reps are working hard compound eye (green) is putting together this years’ newsletter. It’s been great to make the event bigger and better for next year! The composed of several hundred simple units called ommatidia to hear what our members have been up to, and I social events were well attended including the now arranged in an extremely hope you will enjoy reading it. infamous annual “Pub Quiz” and disco after the regular array. The giant conference dinner. Members will be relieved to know polyploidy cells of the fat body (red), the fly equivalent of the The 2016 BSCB/DB spring meeting, organised by our we aren’t including any photos from that here. mammalian liver and adipose committee members Buzz Baum (UCL), Silke tissue, occupy a big area of the Robatzek and Steve Royle, had a particular focus on In this issue, we highlight the great work the BSCB head. Cells and Tissue Architecture, Growth & Cell Division, has been doing to engage young scientists.
    [Show full text]
  • Feedback Interactions Between Cell–Cell Adherens Junctions and Cytoskeletal Dynamics in Newt Lung Epithelial Cells□V Clare M
    Molecular Biology of the Cell Vol. 11, 2471–2483, July 2000 Feedback Interactions between Cell–Cell Adherens Junctions and Cytoskeletal Dynamics in Newt Lung Epithelial Cells□V Clare M. Waterman-Storer,*†‡ Wendy C. Salmon,†‡ and E.D. Salmon‡ *Department of Cell Biology and Institute for Childhood and Neglected Diseases, The Scripps Research Institute, La Jolla, California 92037; and ‡Department of Biology, University of North Carolina, Chapel Hill, North Carolina 27599 Submitted February 3, 2000; Revised April 20, 2000; Accepted May 11, 2000 Monitoring Editor: Jennifer Lippincott-Schwartz To test how cell–cell contacts regulate microtubule (MT) and actin cytoskeletal dynamics, we examined dynamics in cells that were contacted on all sides with neighboring cells in an epithelial cell sheet that was undergoing migration as a wound-healing response. Dynamics were recorded using time-lapse digital fluorescence microscopy of microinjected, labeled tubulin and actin. In fully contacted cells, most MT plus ends were quiescent; exhibiting only brief excursions of growth and shortening and spending 87.4% of their time in pause. This contrasts MTs in the lamella of migrating cells at the noncontacted leading edge of the sheet in which MTs exhibit dynamic instability. In the contacted rear and side edges of these migrating cells, a majority of MTs were also quiescent, indicating that cell–cell contacts may locally regulate MT dynamics. Using photoactivation of fluorescence techniques to mark MTs, we found that MTs in fully contacted cells did not undergo retrograde flow toward the cell center, such as occurs at the leading edge of motile cells. Time-lapse fluorescent speckle microscopy of fluorescently labeled actin in fully contacted cells revealed that actin did not flow rearward as occurs in the leading edge lamella of migrating cells.
    [Show full text]
  • Identification of Endogenous Adenomatous Polyposis Coli Interaction Partners 1 and Β-Catenin-Independent Targets by Proteomics
    Author Manuscript Published OnlineFirst on June 3, 2019; DOI: 10.1158/1541-7786.MCR-18-1154 Author manuscripts have been peer reviewed and accepted for publication but have not yet been edited. 1 Identification of endogenous Adenomatous polyposis coli interaction partners 2 and E-catenin-independent targets by proteomics 3 4 Olesja Popow1,2, João A. Paulo2, Michael H. Tatham3, Melanie S. Volk5, Alejandro 5 Rojas-Fernandez4, Nicolas Loyer5, Ian P. Newton5, Jens Januschke5, Kevin M. 6 Haigis1,6, Inke Näthke5* 7 8 1Cancer Research Institute and Department of Medicine, Beth Israel Deaconess 9 Medical Center, Boston, MA 02215, United States 10 2Department of Cell Biology, Harvard Medical School, Boston, MA 02115, United States 11 3Centre for Gene Regulation and Expression, School of Life Sciences, University of 12 Dundee, Dundee, DD1 5EH, Scotland UK 13 4Center for Interdisciplinary Studies on the Nervous System (CISNe) and Institute of 14 Medicine, Universidad Austral de Chile, Valdivia, Chile 15 5Cell and Developmental Biology, School of Life Sciences, University of Dundee, 16 Dundee, DD1 5EH, Scotland UK 17 6Harvard Digestive Disease Center, Harvard Medical School, Boston, MA 02215, United 18 States 19 20 Running title: The APC interactome and its E-catenin-independent targets. 21 22 Keywords: Adenomatous polyposis coli, destruction complex, colorectal cancer, 23 proteomics, Misshapen-like kinase 1. 1 Downloaded from mcr.aacrjournals.org on October 3, 2021. © 2019 American Association for Cancer Research. Author Manuscript Published OnlineFirst on June 3, 2019; DOI: 10.1158/1541-7786.MCR-18-1154 Author manuscripts have been peer reviewed and accepted for publication but have not yet been edited.
    [Show full text]
  • BSCB Newsletter 2019A:BSCB Aut2k7
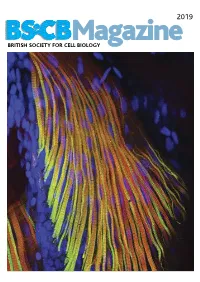
    2019 BSCB Magazine BRITISH SOCIETY FOR CELL BIOLOGY 2019 CONTENTS BSCB Magazine News 2 Book reviews 8 Features 9 Meeting Reports 21 Summer students 25 Society Business 32 Editorial Front cover: microscopic Welcome to the 2019 BSCB Magazine! This year Mustafa Aydogan (University of Oxford), as well as to structure of pectoral fin and Susana and Stephen are filling in for our Newsletter BSCB postdoc poster of the year winners Dr Anna hypaxial muscles of a zebrafish Editor Ann Wheeler. We hope you will enjoy this Caballe (University of Oxford) and Dr Agata Gluszek- Danio rerio larvae at four days year’s magazine! Kustusz (University of Edinburgh). post fertilization. The immunostaining highlights the This year we had a number of fantastic one day In 2019, we will have our jointly BSCB-BSDB organization of fast (red) and meetings sponsored by BSCB. These focus meetings Spring meeting at Warwick University from 7th–10th slow (green) myosins. All nuclei are great way to meet and discuss your science with April, organised by BSCB members Susana Godinho are highlighted in blue (hoechst). experts in your field and to strengthen your network of and Vicky Sanz-Moreno. The programme for this collaborators within the UK. You can read more about meeting, which usually provides a broad spectrum of these meetings in the magazine. If you have an idea themes, has a focus on cancer biology: cell for a focus one day meeting, check how to apply for migration/invasion, organelle biogenesis, trafficking, funding on page 4. Our ambassadors have also been cell-cell communication.
    [Show full text]
  • University of Dundee Inke Näthke Sedwick, C.; Nathke, Inke
    University of Dundee Inke Näthke Sedwick, C.; Nathke, Inke Published in: Journal of Cell Biology DOI: 10.1083/jcb.1895pi Publication date: 2010 Document Version Publisher's PDF, also known as Version of record Link to publication in Discovery Research Portal Citation for published version (APA): Sedwick, C., & Nathke, I. (2010). Inke Näthke: The ABCs of APC. Journal of Cell Biology, 189(5), 774-775. https://doi.org/10.1083/jcb.1895pi General rights Copyright and moral rights for the publications made accessible in Discovery Research Portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from Discovery Research Portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain. • You may freely distribute the URL identifying the publication in the public portal. Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Download date: 01. Oct. 2021 Published May 31, 2010 People & Ideas Inke Näthke: The ABCs of APC Näthke investigates the many functions of adenomatous polyposis coli protein and its contribution to human disease. ighty percent of human colon can- I wanted to go to a foreign country, to cers carry a mutation in adenoma- experience a different way of life, and E tous polyposis coli (APC) protein.
    [Show full text]
  • Isscr 2013 Program Book
    11TH ANNUAL MEEtiNG, BostoN, MA USA ™ BD LSRFortessa X-20 with BD reagents Dear Colleagues: A brilliant new approach to multicolor cell analysis on the benchtop. On behalf of the International Society for Stem Cell Research, we are delighted to welcome you to our 11th Annual Meeting, the largest forum for stem cell and regenerative medicine professionals from around the world. It is also a pleasure to be back in Boston, a historic city that played a key role in the ISSCR’s development, and which features a vibrant stem cell research, biotech, and life science research community. The primary goal of our annual meeting is to provide you with an unparalleled array of opportunities to learn from and interact with your peers, and this year you’ll have more ways to do that than ever before. Additional Poster Session We enjoyed a record number of submitted poster abstracts for 2013. In response to past attendees’ requests for additional time to view and discuss poster presentations, we’ve added a third poster session, giving you a quick and efficient way to keep abreast of the latest scientific advances. “Poster Teasers” and New “Poster Briefs” In 2011, we introduced “poster teasers,” which gave delegates time to share their findings in plenary sessions via 1-minute discussions. They’ve proved so popular with attendees that this year, we’re adding “poster briefs,” 3-minute mini-presentations that give authors of the most highly-rated poster abstracts an opportunity to discuss their work during the concurrent sessions. The burgeoning interest in stem cell research is reflected in our record number of exhibitors this year, 26% of whom are new.
    [Show full text]
  • June 2007 ASCB Newsletter
    ASCB JUNE 2 0 0 7 NEWSLETTER V O L U M E 3 0 , N U M B E R 6 E.B Wilson ASCB Council Held First Retreat, Medalists Page 3 Approved Significant Changes Before devoting one-and-one-half days to stra- ❏ To expand networking and Annual tegic planning, the ASCB Council condensed collaboration prospects for ASCB other business into a half members at all career Meeting day on May 21. At the stages (see ASCB Bethesda, MD, Council fellowship available Program Meeting, Council mem- below) Page 8 bers: ■ Approved new ASCB ■ Discussed defining and Committee Female the Council Affiliate members position (announced ■ Voted to Behavior… in the February 2007 discontinue print copies ASCB Newsletter) of Molecular Biology Leader as one in which a of the Cell (MBC) and Left to right: ASCB Executive Director Joan Goldberg local member is Behavior and ASCB President Bruce Alberts eliminate author color empowered to plan Page 20 charges as of January ASCB regional meetings: 2008, as recommended by MBC Editor- ❏ To offer mentorship, career guidance, in-Chief Sandra Schmid and Director of policy contacts, and presentation Publications Mark Leader Inside opportunities to students and postdocs See Council, page 4 President’s Column 2 E.B. Wilson Medalists 3 Program Development & Did You WICB Report 6 Proposal Writer Wanted WICB Awardees 6 Know …? Annual Meeting Program 8 ASCB seeks a postdoc, regular, or emeritus member with ■ ASCB members are eligible for InCytes from MBC 10 expertise in developing educational programs and writing grant applications for same. Position may be part-time in special discounts on Avis and Public Policy Report 11 the Society’s Bethesda, MD, office or as a consultant, work- Hertz car rentals.
    [Show full text]
  • Cell Biology's Journal
    BoothStop #1203 By More Imaging With Molecular Devices’ complete turnkey solutions for high-content screening, expect more imaging from your screening, more easily and affordably than ever before. More Imaging Systems ULTRA New ImageXpress ™ confocal high-content screening system INSTRUMENTS MICRO ImageXpress ™ high-content screening system ASSAYS ImageXpress® 5000A for live-cell and kinetic assays SOFTWARE INFORMATICS More Software DATA MANAGEMENT MetaXpress™ for uniform image acquisition, processing and analysis Application Modules for validated turnkey analysis of high- content images AcuityXpress™ database-driven cellular informatics software for efficient yet powerful data mining and statistical capabilities MetaMorph®: the gold standard for research microscopy More Assays Transfluor® high-content assays for GPCR activation Expect more. We’ll do our very best to exceed your expectations. now part of MDS Analytical Technologies tel. +1-800-635-5577 | www.moleculardevices.com www.roche-applied-science.com FuGENE® HD Transfection Reagent Measure the results of your transfection, not your transfection reagent. Are you confident that the cellular effects you observe are the result of your 2000 transfected plasmid? Or are your results due to differential gene expression caused ■ 1741 Genes affected by only this reagent by the transfection reagent you use? 1500 ■ Genes affected by Rely on FuGENE® HD Transfection Reagent to avoid the high levels of nonspecific, both reagents off-target effects that can be generated with other transfection reagents (Figure 1). 1000 1505 ■ Generate physiologically relevant data you can trust with a unique non- 500 liposomal formulation. 282 46 ■ Achieve greater cell survival 236 236 when transfecting with this low-cytotoxicity Number of differentially expressed genes 0 reagent that is sterile filtered and free of animal-derived components.
    [Show full text]
  • Hélder José Martins Wlatato Mfcrotubule-ASSOCIATED Proteh KINETOCHORE FUNCTION and Spindle ASSEMBLY Instituto De Ciências
    Hélder José Martins Wlatato MfCROTUBULE-ASSOCIATED PROTEh KINETOCHORE FUNCTION AND SPiNDLE ASSEMBLY Instituto de Ciências Biomédicas de Abei Salazar Universidade do Porto PORTO, 2002 Hélder José Martins Maiato MICROTUBULE-ASSOCIATED PROTEINS IN KINETOCHORE FUNCTION AND SPINDLE ASSEMBLY Dissertação realizada para candidatura ao grau de Doutor em Ciências Biomédicas submetida ao Instituto de Ciências Biomédicas de Abel Salazar da Universidade do Porto Supervisor: Professor Claudio E. Sunkel, Universidade do Porto Co-Supervisor: Professor William C. Earnshaw, University of Edinburgh PORTO 2002 Dedicated to my wife and parents for their love and encouraging, to Claudio and Bill for giving me the opportunity to learn about cells, and to the memory of Theodor Boveri and Daniel Mazia, whose work has inspired me in the study of mitosis. Acknowledgements I would like to reserve this space to express my gratitude to the people that made this work possible. I start by thanking to the Gulbenkian PhD Programme in Biology and Medicine, namely to Prof. António Coutinho, for giving me and many others the opportunity to learn more about Biology and for the nobility to invest and form young scientists. Additionally, I would like to acknowledge the Programme and Fundação para a Ciência e Tecnologia for financial support during the last four years. I wish to address a very special thanks to Prof. Claudio Sunkel at the University of Porto, who always believed in this project, for allowing me to work in his lab, for giving me the freedom of experimentation and for his great encouraging and trust about my work. I would like to thank to Prof.
    [Show full text]
  • Mathematical Biology of the Cell: Cytoskeleton and Motility July 31 – August 5, 2011
    Mathematical Biology of the Cell: Cytoskeleton and Motility July 31 – August 5, 2011 MEALS *Breakfast (Buffet): 7:00 – 9:30 am, Sally Borden Building, Monday – Friday *Lunch (Buffet): 11:30 am – 1:30 pm, Sally Borden Building, Monday – Friday *Dinner (Buffet): 5:30 – 7:30 pm, Sally Borden Building, Sunday – Thursday Coffee Breaks: 2nd floor lounge, Corbett Hall *Please remember to scan your meal card at the host/hostess station in the dining room for each meal. MEETING ROOMS All lectures will be held in Max Bell 159 (Max Bell Building accessible by walkway on 2nd floor of Corbett Hall). LCD projector, overhead projectors and blackboards are available for presentations. Note that the meeting space designated for BIRS is the lower level of Max Bell, Rooms 155-159. Please respect that all other space has been contracted to other Banff Centre guests, including any Food and Beverages in those areas. SCHEDULE Sunday 16:00 Check-in begins (Front Desk – Professional Development Centre - 24 hours) 17:30-19:30 Dinner 20:00 Informal gathering in 2nd floor lounge, Corbett Hall Beverages and snacks are available on a cash honor system. Monday 7:00-8:30 Breakfast 8:30-8:45 Welcome and Introduction 8:45-9:25 Alexander Verkhovsky, EPFL Lausanne Interplay between cytoskeletal forces, membrane tension, and hydrostatic pressure in rapidly migrating cells 9:25-10:05 Jay Tang, Brown University A multiple spring model that predicts bipedal motion of crawling cells 10:05-10:30 Coffee Break 10:30-11:10 Alex Mogilner, University of California, Davis Mechanical
    [Show full text]
  • REVIEW E V I E W Focus on DEVELOPMENT and DISEASE
    REVIEW FOCUs ON DEVELOPMENT AND DISEASE Cell polarity in development and cancer Andreas Wodarz and Inke Näthke The development of cancer is a multistep process in which the DNA of a single cell accumulates mutations in genes that control essential cellular processes. Loss of cell–cell adhesion and cell polarity is commonly observed in advanced tumours and correlates well with their invasion into adjacent tissues and the formation of metastases. Growing evidence indicates that loss of cell–cell adhesion and cell polarity may also be important in early stages of cancer. The strongest hints in this direction come from studies on tumour suppressor genes in the fruitfly Drosophila melanogaster, which have revealed their importance in the control of apical–basal cell polarity. Most human cancers are derived from epithelial tissues, which are char- Loss of E-cadherin: a critical step in the development of cancer acterized by a specific cellular architecture (Fig. 1). Junctions between The establishment of cell polarity in epithelia depends on the for- neighbouring epithelial cells allow the separation of apical and basola- mation of cell–cell adherens junctions3. E-cadherin is a key factor in teral membrane domains that vary in protein and lipid content, and the junction formation (Fig. 1): in addition to providing the physical link polarity that results is crucial to normal cell function. Important hall- between neighbouring cells and intracellular structures, cadherins sup- marks of advanced cancerous tumours are the loss of epithelial character port the assembly of large signalling complexes4. Loss of E-cadherin is from the original tissue and the appearance of more mesenchymal-like implicated in later stages of tumorigenesis and commonly correlates cells, especially at the periphery, where the tumour cells are in contact with a more invasive phenotype5,6.
    [Show full text]
  • Cell Biology, Members in the News 8 Disparities Research in Has Been Named Member Gifts 8 HIV, to Present the 15Th by ASCB Public Policy Briefing 9 Annual E.E
    ASCB AUGUST 2008 NEWSLETTER VOLUME 31, NUMBER 8 Making Expanding Scientific Exchange, Education a Priority Building Capacity Page 2 Involving more members in the ASCB’s programs was one focus of the June 19, 2008, meeting of the Society’s International Affairs Committee (IAC). The meeting, held in Bethesda, MD, A New ASCB also addressed IAC goals and related activities: Education n Promoting scientific exchange internationally n Building scientific capacity worldwide Initiative n Supporting international ASCB members in their scientific endeavors Page 12 Promoting Scientific Exchange IAC Co-Chairs Mary C. Beckerle and Bruce M. Alberts, ASCB Past President, welcomed The Science Committee members Dacheng He, Cynthia G. Jensen, J. Richard (Dick) McIntosh, Mahasin A. Osman, Mark Peifer, and David S. Roos; and staff members Trina Armstrong, Howie Berman, Mentoring Thea Clarke, David Driggers, Dave Ennist, Joan Goldberg, and Alison Harris for all or part of Paradox the meeting. Beckerle reported on: n The 2007 ASCB Council Roundtable, where approximately 200 U.S. and international graduate Page 19 students discussed with ASCB Council members and staff how the Society could help them See IAC, continued on page 6 Inside Hildreth Named Gall to Present President’s Column 2 Alberts Award 7 E.E. Just Lecturer Porter Lecture MBC Paper of the Year 7 The ASCB Minorities Affairs Committee has Joseph Gall of the Carnegie Institution Public Service Award 8 named James Earl King Hildreth, Director of the of Washington, a founder of the field Meharry Center for Health of cell biology, Members in the News 8 Disparities Research in has been named Member Gifts 8 HIV, to present the 15th by ASCB Public Policy Briefing 9 annual E.E.
    [Show full text]