A Systematic Method of Optimization of Machining Parameters Considering Energy Consumption, Machining Time and Surface Roughness with Experimental Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

60" Workbench
Owner’s Manual & Safety Instructions Save This Manual Keep this manual for the safety warnings and precautions, assembly, operating, inspection, maintenance and cleaning procedures. Write the product’s serial number in the back of the manual near the assembly diagram (or month and year of purchase if product has no number). Keep this manual and the receipt in a safe and dry place for future reference. ITEM 69054 60" Workbench Visit our website at: http://www.harborfreight.com Email our technical support at: [email protected] When unpacking, make sure that the product is intact and undamaged. If any parts are missing or broken, please call 1-800-444-3353 as soon as possible. Copyright© 2012 by Harbor Freight Tools®. All rights reserved. No portion of this manual or any artwork contained herein may be reproduced in Read this material before using this product. any shape or form without the express written consent of Harbor Freight Tools. Failure to do so can result in serious injury. Diagrams within this manual may not be drawn proportionally. Due to continuing SAVE THIS MANUAL. improvements, actual product may differ slightly from the product described herein. Tools required for assembly and service may not be included. Table of Contents Safety ......................................................... 2 Parts List and Diagram .............................. 10 Specifications ............................................. 3 Warranty .................................................... 12 Setup .......................................................... 3 SA F ET Y WARNING SYMBOLS AND DEFINITIONS This is the safety alert symbol. It is used to alert you to potential personal injury hazards. Obey all safety messages that follow this symbol to avoid possible injury or death. Indicates a hazardous situation which, if not avoided, will result in death or serious injury. -

Paul Sellers' Workbench Measurements and Cutting
PAUL SELLERS’ WORKBENCH MEASUREMENTS AND CUTTING LIST PAUL SELLERS’ WORKBENCH MEASUREMENTS AND CUTTING LIST NOTE When putting together the cutting list for my workbench, I worked in imperial, the system with which I am most comfortable. I was not happy, however, to then provide direct conversions to metric because to be accurate and ensure an exact fit this would involve providing measurements in fractions of millimetres. When I do work in metric I find it more comfortable to work with rounded numbers, therefore I have created two slightly different sets of measurements. This means that in places the imperial measurement given is not a direct conversion of the metric measurement given. Therefore, I suggest you choose one or other of the systems and follow it throughout. © 2017 – Paul Sellers v2 PAUL SELLERS’ WORKBENCH MEASUREMENTS AND CUTTING LIST WOOD QTY DESCRIPTION SIZE (IMPERIAL) SIZE (METRIC) (THICK X WIDE X LONG) (THICK X WIDE X LONG) 4 Leg 2 ¾” x 3 ¾” x 34 ⅜” 70 x 95 x 875mm 1 Benchtop 2 ⅜” x 12” x 66” 65 x 300 x 1680mm 2 Apron 1 ⅝” x 11 ½” x 66” 40 x 290 x 1680mm 1 Wellboard 1” x 12 ½” x 66” 25 x 320 x 1680mm 4 Rail 1 ½” x 6” x 26” 40 x 150 x 654mm 2 Bearer 1 ¼” x 3 ¾” x 25” 30 x 95 x 630mm 4 Wedge ⅝” x 1 ½” x 9” 16 x 40 x 228mm 4 Wedge retainer ⅝” x 1 ½” x 4” 16 x 40 x 100mm HARDWARE QTY DESCRIPTION SIZE (IMPERIAL) SIZE (METRIC) 1 Vise 9” 225mm Dome head bolts (including nuts and washers) for 4 ⅜” x 5” 10 x 130mm bolting legs to aprons 2 Lag screws (with washers) for underside of vise ½” x 2 ½” 12 x 65mm 2 Lag screws for face -

SHAKERWORKBENCH Design, Construction Notes and Techniques
BENCHCRAFTED · SHAKER BENCH PLANS SHAKERWORKBENCH Design, Construction Notes and Techniques “Don't make something unless it is both necessary and useful; but if it is both neces- sary and useful, don't hesitate to make it beautiful." –Shaker Dictum Introduction and Design: Ron Brese Construction Notes and Techniques: Jameel Abraham Measured Drawings: Louis Bois Copyright Benchcrafted 2011·2014 No unauthorized reproduction or distribution. You may print copies for your own personal use only. 1 BENCHCRAFTED · SHAKER BENCH PLANS · INTRODUCTION & DESIGN · “Whatever perfections you may have, be assured people will find them out, but whether they do or not, nobody will take them on your word” Canterbury, New Hampshire, 1844 When I first laid eyes on the workbench at the Hancock Shaker Museum in Pittsfield, Massachusetts I had a pretty good idea of the configuration of my next workbench. I think it would be safe to say that I was inspired. However, designing a workbench that is inspired by a Shaker icon can be intimidating as well. I had to do justice to the original and keep in mind what might be considered acceptable. Luckily, most are aware that the Shakers were quite accepting of new technologies that could be practically applied, so this did allow a fair amount of leeway in regards to using more recent workholding devices on this bench. In the end, I did want the look to be very representative of the Shaker Ideal. “‘Tis a Gift to Be Simple” is an over used Shaker pronouncement, however I often think it’s meaning is misinterpreted. I believe it means having freedom from making things unnecessarily complicated. -

Woodworking Glossary, a Comprehensive List of Woodworking Terms and Their Definitions That Will Help You Understand More About Woodworking
Welcome to the Woodworking Glossary, a comprehensive list of woodworking terms and their definitions that will help you understand more about woodworking. Each word has a complete definition, and several have links to other pages that further explain the term. Enjoy. Woodworking Glossary A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | #'s | A | A-Frame This is a common and strong building and construction shape where you place two side pieces in the orientation of the legs of a letter "A" shape, and then cross brace the middle. This is useful on project ends, and bases where strength is needed. Abrasive Abrasive is a term use to describe sandpaper typically. This is a material that grinds or abrades material, most commonly wood, to change the surface texture. Using Abrasive papers means using sandpaper in most cases, and you can use it on wood, or on a finish in between coats or for leveling. Absolute Humidity The absolute humidity of the air is a measurement of the amount of water that is in the air. This is without regard to the temperature, and is a measure of how much water vapor is being held in the surrounding air. Acetone Acetone is a solvent that you can use to clean parts, or remove grease. Acetone is useful for removing and cutting grease on a wooden bench top that has become contaminated with oil. Across the Grain When looking at the grain of a piece of wood, if you were to scratch the piece perpendicular to the direction of the grain, this would be an across the grain scratch. -

Modular Wood Top Workbench
ASSEMBLY INSTRUCTIONS & PARTS MANUAL Modular Workbench with Hardwood Butcher Block Top RETAIN INSTRUCTIONS FOR FUTURE REFERENCE LOAD CAPACITIES FOR BUTCHER BLOCK TOP UNIT SIZE WT. CAPACITY 48w x 30d 4000 lbs. 60w x 30d 3800 lbs. 72w x 30d 3600 lbs. 96w x 30d 4000 lbs. 60w x 36d 3800 lbs. 72w x 36d 3600 lbs. 96w x 36d 4000 lbs. The following instructions also can be used if a Plastic Laminate top or Compressed Wood top was purchased. LOAD CAPACITIES LOAD CAPACITIES FOR PLASTIC LAMINATE TOP FOR COMPRESSED WOOD TOP UNIT SIZE WT. CAPACITY UNIT SIZE WT. CAPACITY 48w x 30d 1200 lbs. 48w x 30d 2400 lbs. 60w x 30d 800 lbs. 60w x 30d 1900 lbs. 72w x 30d 750 lbs. 72w x 30d 1500 lbs. 96w x 30d 1200 lbs. 96w x 30d 2400 lbs. 60w x 36d 800 lbs. 60w x 36d 1900 lbs. 72w x 36d 750 lbs. 72w x 36d 1500 lbs. 96w x 36d 1200 lbs. 96w x 36d 2400 lbs. NOTE: Additional accessories shown above are sold separately. GENERAL SAFETY INFORMATION Some parts may have sharp edges. CARE must be taken when handling various pieces to avoid injury. For safety, wear a pair of work gloves when assembling or performing any maintenance on units. LIMITED WARRANTY Tennsco warrants goods purchased hereunder to be free of defects in materials and workmanship for a period of one (1) year from the date of shipment, hereunder. This warranty shall not apply in the event goods are damaged as a result of misuse, abuse, neglect, accident, improper application, modification or repair by persons not authorized by Seller, where goods are damaged during shipment, or where the date stamps on the goods have been defaced, modified or removed. -

User Manual Workbench
User Manual Workbench Create and Customize User Interfaces for Router Control www.s-a-m.com WorkBench User Manual Issue1 Revision 5 Page 2 © 2017 SAM WorkBench User Manual Information and Notices Information and Notices Copyright and Disclaimer Copyright protection claimed includes all forms and matters of copyrightable material and information now allowed by statutory or judicial law or hereinafter granted, including without limitation, material generated from the software programs which are displayed on the screen such as icons, screen display looks etc. Information in this manual and software are subject to change without notice and does not represent a commitment on the part of SAM Limited. The software described in this manual is furnished under a license agreement and can not be reproduced or copied in any manner without prior agreement with SAM Limited, or their authorized agents. Reproduction or disassembly of embedded computer programs or algorithms prohibited. No part of this publication can be transmitted or reproduced in any form or by any means, electronic or mechanical, including photocopy, recording or any information storage and retrieval system, without permission being granted, in writing, by the publishers or their authorized agents. SAM operates a policy of continuous improvement and development. SAM reserves the right to make changes and improvements to any of the products described in this document without prior notice. Contact Details Customer Support For details of our Regional Customer Support Offices and contact details please visit the SAM web site and navigate to Support/247-Support. www.s-a-m.com/support/247-support/ Customers with a support contract should call their personalized number, which can be found in their contract, and be ready to provide their contract number and details. -

Wood Has a Grain
THE WAY WOOD WORKS Everything you wanted to know about wood but didn't know what to ask. By Nick Engler ood is a cantankerous substance; there's no two ways about it. It's virtues, of course are legendary. It's attractive, abundant, and easy to work. Pound for pound, it's stronger than steel. W If properly finished and cared for it will last indefinitely. But none of that makes up for the fact that it's a complex — and often perplexing — building material. Unlike metals and plastics, whose properties are fairly consistent, wood is wholly inconsistent. It expands and contracts in all directions, but not at the same rate. It's stronger in one direction than it is in another. Its appearance changes not only from species to species, but from log to log — sometimes board to board. That being so, how can you possibly use this stuff to make a fine piece of furniture? Or a fine birdhouse, for that matter? To work wood — and have it work for you — you must understand three unique properties of wood that affect everything you make: • Wood has grain. • Wood moves more across the grain than along it. • Wood has more strength along the grain than across it. Sounds trite, I know. These are “everyone-knows-that” garden-variety facts. But there is more grist here for your woodworking mill than might first appear. Wood has grain As a tree grows, most of the wood cells align themselves with the axis of the trunk, limb, or root. These cells are composed of long, thin bundles of fibers, about 100 times longer than they are wide. -

CLASSIC WORKBENCH Design, Construction Notes & Techniques
BENCHCRAFTED CLASSIC WORKBENCH Design, Construction Notes & Techniques Copyright, Benchcrafted December 2016 www.benchcrafted.com 1 DESIGN When we set out to design a new workbench for our customers, from the very beginning we decided it should, above all, be simple. Not only in function, but also to build. We make no bones about it, our vises are designed and made to work sweetly, but not to a price point. However, not everyone is ready for their ultimate Split Top Roubo bench build, either monetarily, or technically. For those looking to get their feet wet in traditional woodworking, using time-proven techniques and tools, this bench will provide all the workholding required to test the waters. For many, this will be all the bench you need, and for others it will be an excellent springboard to our Split Top Roubo, while keeping the Classic as a second bench. The Classic Workbench is based largely on the famous Plate 11 workbench from Roubo’s “The Art of the Joiner”. We’ve built dozens of these “Roubo” benches over the past decade, helped others build hundreds more and examined extant French benches from the period. We’ve haven’t changed our opinion on this fundamental design. The Classic is a simpler, easier to build version of Roubo’s Plate 11 bench that captures all the functionality of Roubo’s design. French technical schools of the late 19th and early 20th centuries were outfitted with benches just like this. Paring down the bench to its essentials, we’ve incorporated our Classic Leg Vise, Planing Stop and Holdfast as workholding devices. -

Workbench No
TOOL REVIEW: 9 Router Tables Under$ 300 TM Woodworking To Improve Your Home Storage with Style! Cedar Garden Shed Plus: ● Stack 'em Up Storage Bins ● Trouble-Free Pocket Doors ● 5 Energy-Saving Tune-Up Tips www.WorkbenchMagazine.com No 267 September/October 2001 Contents 16 16 Cedar Garden Shed Why settle for oversized pre-fab when you can build the perfect-sized shed yourself from scratch? We’ll show you some construction techniques that can be used in all types of projects. 18 Modular Design . Basic framing makes building this shed simple. 20 Roofing Systems . Learn how to build rafters and install shingles. 22 Trim and Siding ...Pick up a few tips for applying cedar lap siding. 18 20 22 24 28 Easy Way Install a to Hang Trouble-Free Double Doors Pocket Door Hanging your own No room for a hinged doors is the way to go door? No problem. when you want to save We’ll show you how to money and get just the install a door that look you’re after for “disappears” into a your new shed. pocket in the wall. 24 28 2 WORKBENCH ■ SEPTEMBER | OCTOBER 2001 TM 34 34 Router Table Review A router table doesn’t have to be expensive to get the job done. We tested nine models — all for less than $300. Find out which one takes the “top table” award. 40 Stackable Storage Bins A simple system of interlocking keys and notches makes these stacking storage bins as sturdy as they are versatile. 40 46 46 5 Energy-Saving Tune-Up Tips Practical ways to button-up your home and take the chill out of those winter energy bills. -
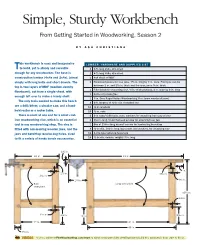
Simple, Sturdy Workbench from Getting Started in Woodworking, Season 2
Simple, Sturdy Workbench From Getting Started in Woodworking, Season 2 BY ASA CHRISTIANA his workbench is easy and inexpensive LUMBER, HARDWARE AND SUPPLIES LIST Tto build, yet is sturdy and versatile 4 8-ft.-long 2x4s, kiln-dried enough for any woodworker. The base is 2 8-ft.-long 4x4s, kiln-dried construction lumber (4x4s and 2x4s), joined 1 4x8 sheet of MDF simply with long bolts and short dowels. The 2 Hardwood pieces for vise jaws, 71/2 in. long by 3 in. wide. Front jaw can be top is two layers of MDF (medium-density between 1 in. and 11/2 in. thick and the rear jaw is 3/4 in. thick. 1 Filler block for mounting vise, 3/4-in.-thick plywood, 4 in. wide by 6 in. long fiberboard), cut from a single sheet, with 1 bottle of yellow glue enough left over to make a handy shelf. 1 7-in. Groz Rapid-Action Woodworking Vise (www.woodcraft.com) The only tools needed to make this bench 4 6-ft. lengths of 3⁄8-in.-dia. threaded rod are a drill/driver, a circular saw, and a hand- 16 3⁄8-in. washers held router or a router table. 16 3⁄8-in. nuts There is room at one end for a small cast- 2 2-in.-long 1/4-20 bolts, nuts, washers for attaching front jaw of vise iron woodworking vise, which is an essential 2 11/2-in.-long, 1/4-20 flathead screws for attaching rear jaw tool in any woodworking shop. -

The Workbench
W ENJOY THIS SELECTION FROM The Workbench To purchase The Workbench, make your selection now: • ebook version • traditional version BUY NOW! BUY NOW! 6 Bench in a Box Woodworkers are do-it-yourselfers by nature. As a group, we’re somewhat on the thrifty side as well. We often presume that building a bench is more economical than buying one. But when you add up the cost of lumber, hardware, and other materials, prefabricated benches don’t look so expensive after all. And if you make a realistic estimate of the time involved, even figuring minimum wage as an hourly rate, chances are you’re money ahead buying a bench and paying the hefty freight for having it delivered. The desire to build a workbench is never entirely rational. But most of us opt to purchase rather than build components. There may be some portion of the building process that suits you more than others. Perhaps building the benchtop chal- lenges your time or resources enough for you to contemplate __________________________ alternatives to building from scratch. AHIGH-QUALITY WORKBENCH by any standard, this Once you begin purchasing components, it’s a short leap Ultimate American model to purchasing the entire bench. Among the offerings of work- from Diefenbach would be a welcome addition to bench manufacturers, you might find exactly the right bench. any shop large enough to accommodate its nearly 8-ft. length. 108 BENCH IN A BOX flat. So it’s no surprise that benchtops are a Bench Components popular commercial item. Butcher block sold Only 20 years ago woodworkers had many for countertops is now available in lumberyards, fewer options in commercially available bench home centers, and just about any outlet that parts. -

Modern Hardware and Techniques Update This Tage Frid-Inspired Bench
Scandinavian Workbench BY BILL RAINFORD Modern hardware and techniques update this Tage Frid-inspired bench. 02 ■ POPULAR WOODWORKING MAGAZINE 30_1702_PWM_FridBench.indd 30 11/29/16 9:59 AM candinavian- or Continental- “Take a piece of wood – plane, it’s well-suited for workbench building style workbenches are the vinyl sand, and oil it, and you will fi nd it and relatively plentiful in New England, SLP records of the woodworking a beautiful thing. The more you do where I live. Buy your wood well in world. These iconic benches have never to it from then on, the more chance advance so that you can bring it into left the scene. A few are classics and oth- that you will make it worse.” your shop, sticker it and allow it to ac- ers are the fl avor of the month. Some Tage Frid (1915-2004), climate to your shop for at least a week. benches in this style are masterworks Danish-born woodworking teacher, While the wood acclimates, gather and some are poor approximations of furniture maker and author all your hardware and vises, and note an archetypical form. The trick is fi nd- any changes you need to make to your ing the workbench that hits all the right joiner y or de sign to fi t your hardware. notes for how you work so you can go I was inspired by Frid’s bench – but I Once the wood is acclimated, plane, rip on to create your own opus. also listened to the criticisms. Some and buck the pieces close to their fi nal folks complained about the relatively sizes – but leave them a bit oversized What’s Old is New Again short length, which was designed for and again sticker them for a couple of Much as how Roubo and Nicholson a modest cabinetmaker in a classroom days.