DOCSLIB.ORG

Lecture 23. Read-Only Memories & Programmable Logic Arrays

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 23. Read-Only Memories & Programmable Logic Arrays EE 280 Introduction to Digital Logic Design Lecture 23. Read-Only Memories & Programmable Logic Arrays EE280 Lecture 23 23 - 1 Read-Only Memories Memory is like an array of mailboxes (registries of binary data) A stored array of binary data which can be read only, but not changed In general, 2n × m ROM ≡ I/P lines ≡ O/P lines ≡ words* each bits long For each combination of inputs on the n input lines, the corresponding pattern of 0’s and 1’s (a word) is generated on the m output lines - typical sizes range from (32 words x 4 bits) to (512K words x 8 bits) or larger EE280 Lecture 23 23 - 2 1 ROM Realization of Logic Functions A B C F0 F1 F2 F3 0 0 0 A ROM 0 0 1 B 8 words 0 1 0 C x 4 bits 0 1 1 1 0 0 1 0 1 F F F F 1 1 0 0 1 2 3 1 1 1 a. Block diagram b. Truth table for ROM F0 = = A'B' + AC‘ F1 = = B + AC‘ F2 = = A'B' + BC‘ F3 = = AC + B EE280 Lecture 23 23 - 3 ROM Realization of Logic Functions ROM consists of a decoder and a memory array. When a particular input sequence is applied to the n decoder inputs, exactly one of the 2n outputs is set to 1. This output line selects one of the words in the memory array. decoder outputs mi are consecutive minterms ROM outputs Fi are generated by ORing selected minterms Switching elements pass 1 to output, otherwise resistors at the top set output to 0 EE280 Lecture 23 23 - 4 2 Code Conversion Network using ROM The ROM realizes conversion between BDC (8421) code and Excess-3 code Decimal Input Output digit ABCD W X Y Z 0 0000 0 0 1 1 A W 1 0001 0 1 0 0 B X 2 0010 0 1 0 1 ROM C Y 3 0011 0 1 1 0 4 0100 0 1 1 1 D Z 5 0101 1 0 0 0 6 0110 1 0 0 1 7 0111 1 0 1 0 8 1000 1 0 1 1 9 1001 1 1 0 0 X 1010 X X X X X 1011 X X X X EE280 Lecture 23 23 - 5 Code Conversion Network using ROM m0 m1 m2 m3 m4 m5 A m6 B m7 m C 8 m9 D DECODER 4-line to 16-line 16-line 4-line to m10 m11 m12 m13 m14 m15 EE280 Lecture 23 23 - 6 3 ROM Realization of Logic Functions Internal structure of a 128 x 1 ROM using two-dimensional decoding - rectangular form reduces complexity and increases flexibility - note the inverted decoder, and +5V on ROM output lines EE280 Lecture 23 23 - 7 ROM Types Mask-programmable (ROM) - Permanent programming done at fabrication time - Diodes blown at factory as per customer order - Very expensive and therefore feasible only for large quantity orders Programmable ROM (PROM) - User programmed after purchase, called field-programmable ROM (FPROM) - Reprogrammable by user, erasable by UV emission, called erasable, programmable ROM (EPROM) Electrically erasable, programmable ROM (EEPROM) - User can erase individual words; switching elements can be enabled/disabled - Can be erased and reprogrammed limited number of times, typically 100 to 1000 times EE280 Lecture 23 23 - 8 4 Programmable Logic Arrays (PLA) Performs the same basic functions as ROM ROM - the inner organization is different - decoder is replaced with an AND array and realizes selected product terms of the input variables - output functions are realized by OR array that Ors together the product terms - PLA implements SOP expressions, while PLA ROM implements a truth table EE280 Lecture 23 23 - 9 Programmable Logic Arrays (PLA) PLA with n I/P's and m O/P's can realize PLA is used instead of ROM when n is large, and number of terms is not large e.g., if n = 16 EE280 Lecture 23 23 - 10 5 Programmable Logic Arrays (PLA) PLA can be represented by a PLA table Inputs Outputs Product terms A B C f1 f2 f3 f4 A’C’ 0 – 0 1 0 1 0 A B’ 1 0 – 0 0 0 1 A C 1 – 1 1 1 0 0 B’C –0 1 0 1 1 1 EE280 Lecture 23 23 - 11 PLA - Example Design PLA that implements following functions a’bd abd … EE280 Lecture 23 23 - 12 6 Programmable Arrays Logic (PAL) The PAL has many features in common with PROM and PLA The PAL is a special case of the of the PLA in which the array is programmable and the array is fixed by the manufacturer Because for PAL only AND array is programmable it is cheaper than PLA; it is also easier to program and therefore often used A’ A B’ B C’ C AND gates with 6 inputs (A’, A, B’, B, C’, C) EE280 Lecture 23 23 - 13 7.
Load more

Recommended publications
  • Error Detection and Correction Methods for Memories Used in System-On-Chip Designs
    International Journal of Engineering and Advanced Technology (IJEAT) ISSN: 2249 – 8958, Volume-8, Issue-2S2, January 2019 Error Detection and Correction Methods for Memories used in System-on-Chip Designs Gunduru Swathi Lakshmi, Neelima K, C. Subhas ABSTRACT— Memory is the basic necessity in any SoC Static Random Access Memory (SRAM): It design. Memories are classified into single port memory and consists of a latch or flipflop to store each bit of multiport memory. Multiport memory has ability to source more memory and it does not required any refresh efficient execution of operation and high speed performance operation. SRAM is mostly used in cache memory when compared to single port. Testing of semiconductor memories is increasing because of high density of current in the and in hand-held devices. It has advantages like chips. Due to increase in embedded on chip memory and memory high speed and low power consumption. It has density, the number of faults grow exponentially. Error detection drawback like complex structure and expensive. works on concept of redundancy where extra bits are added for So, it is not used for high capacity applications. original data to detect the error bits. Error correction is done in Read Only Memory (ROM): It is a non-volatile memory. two forms: one is receiver itself corrects the data and other is It can only access data but cannot modify data. It is of low receiver sends the error bits to sender through feedback. Error detection and correction can be done in two ways. One is Single cost. Some applications of ROM are scanners, ID cards, Fax bit and other is multiple bit.
    [Show full text]
  • Semiconductor Memories
    Semiconductor Memories Prof. MacDonald Types of Memories! l" Volatile Memories –" require power supply to retain information –" dynamic memories l" use charge to store information and require refreshing –" static memories l" use feedback (latch) to store information – no refresh required l" Non-Volatile Memories –" ROM (Mask) –" EEPROM –" FLASH – NAND or NOR –" MRAM Memory Hierarchy! 100pS RF 100’s of bytes L1 1nS SRAM 10’s of Kbytes 10nS L2 100’s of Kbytes SRAM L3 100’s of 100nS DRAM Mbytes 1us Disks / Flash Gbytes Memory Hierarchy! l" Large memories are slow l" Fast memories are small l" Memory hierarchy gives us illusion of large memory space with speed of small memory. –" temporal locality –" spatial locality Register Files ! l" Fastest and most robust memory array l" Largest bit cell size l" Basically an array of large latches l" No sense amps – bits provide full rail data out l" Often multi-ported (i.e. 8 read ports, 2 write ports) l" Often used with ALUs in the CPU as source/destination l" Typically less than 10,000 bits –" 32 32-bit fixed point registers –" 32 60-bit floating point registers SRAM! l" Same process as logic so often combined on one die l" Smaller bit cell than register file – more dense but slower l" Uses sense amp to detect small bit cell output l" Fastest for reads and writes after register file l" Large per bit area costs –" six transistors (single port), eight transistors (dual port) l" L1 and L2 Cache on CPU is always SRAM l" On-chip Buffers – (Ethernet buffer, LCD buffer) l" Typical sizes 16k by 32 Static Memory
    [Show full text]
  • Via-Programmable Read-Only Memory Design for Full Code Coverage Using a Dynamic Bit-Line Shielding Technique
    Via-Programmable Read-Only Memory Design for Full Code Coverage Using A Dynamic Bit-Line Shielding Technique Meng-Fan Chang1, 2, Ding-Ming Kwai2, and Kuei-Ann Wen1 1 Institute of Electronics, National Chiao Tung University, Hsinchu, Taiwan 2 Intellectual Property Library Company, Hsinchu, Taiwan [email protected] Abstract 0-cell 1-cell 0-cell Crosstalk between bit lines leads to read-1 failure Metal-3 (BL) in a high-speed via-programmable read only memory (ROM) and limits the coverage of applicable code Via-2 (Code) patterns. Due to the fluctuations in bit-line intrinsic Metal-2 and coupling capacitances, the amount of noise coupled to a selected bit line may vary, resulting in the Via-1 reduction of sensing margin. In this paper, we propose a dynamic bit-line shielding (DBS) technique, suitable Metal-1 to be implemented in compliable ROM, to eliminate the Contact crosstalk-induced read failure and to achieve full code coverage. Experiments of the 256Kb instances with Diffusion Diffusion Diffusion and without the DBS circuit were undertaken using STI STI STI STI 0.25µm and 0.18µm standard CMOS processes. The test results demonstrate the read-1 failures and Fig. 1. Cross-sectional view of ROM array with via-2 confirm that the DBS technique can remove them codes and metal-3 bit lines. successfully, allowing the ROM to operate under a wide range of supply voltage. sectional view of the memory array with via-2 codes 1. Introduction and metal-3 bit lines. This leads to more severe bit-line crosstalk, since the contact and via at the lower levels Mask-programmable read-only memory (ROM) must be stacked and the metal islands for them to land macros are commonly embedded into system-on-chip upon contribute considerable side-wall capacitances to (SoC) designs today.
    [Show full text]
  • Refresh Operation and Semi-Conductor Rom Memories
    REFRESH OPERATION AND SEMI-CONDUCTOR ROM MEMORIES The Refresh control block periodically generates Refresh, requests, causing the access control block to start a memory cycle in the normal way. This block allows the refresh operation by activating the Refresh Grant line. The access control block arbitrates between Memory Access requests and Refresh requests, with priority to Refresh requests in the case of a tie to ensure the integrity of the stored data. As soon as the Refresh control block receives the Refresh Grant signal, it activates the Refresh line. This causes the address multiplexer to select the Refresh counter as the source and its contents are thus loaded into the row address latches of all memory chips when the RAS signal is activated. During this time the R/ W line may be low, causing an inadvertent write operation. One way to prevent this is to use the Refresh line to control the decoder block to deactivate all the chip select lines. The rest of the refresh cycle is the same as in a normal cycle. At the end, the Refresh control block increments the refresh counter in preparation for the next Refresh cycle. Even though the row address has 8 bits, the Refresh counter need only be 7 bits wide because of the cell organization inside the memory chips. In a 64k x 1 memory chip, the 256x256 cell array actually consists of two 128x256 arrays. The low order 7 bits of the row address select a row from both arrays and thus the row from both arrays is refreshed! Ideally, the refresh operation should be transparent to the CPU.
    [Show full text]
  • Memory Basics
    Memory Basics • RAM: Random Access Memory – historically defined as memory array with individual bit access – refers to memory with both Read and Write capabilities • ROM : Read Only Memory – no capabilities for “online” memory Write operations – Write typically requires high volt ages or erasing by UV light • Volatility of Memory – volatile memory loses data over time or when power is removed • RAM is volatile – non-volatile memory stores data even when power is removed • ROM is non-volatile • Static vs. Dynamic Memory – Static: holds data as long as power is applied (SRAM) – Dynamic: must be refreshed periodically (DRAM) ECE 410, Prof. A. Mason/Prof. F. Salem Lecture Notes 13.1 SRAM Basics • SRAM = Static Random Access Memory – Static: holds data as long as power is applied – Volatile: can not hold data if power is removed • Operation States – 3 states (modes) • hold • write WL • read • Basic 6T (transistor) SRAM Cell – bistable (cross-coupled) INVs for storage – access transistors MAL & MAR MAL MAR • access to stored data for read and write – word line, WL, controls access bit bit • WL = 0, hold operation • WL = 1, read or write operation ECE 410, Prof. A. Mason/Prof. F. Salem Lecture Notes 13.2 SRAM Operations • Hold – word line = 0, access transistors are OFF – data held in latch • Write WL – word line = 1, access tx are ON – new data (voltage) applied to bit and bit_bar – data in latch overwritten with new value MAL MAR • Read bit bit – word line = 1, access tx are ON – bit and bit_bar read by a sense amplifier • Sense Amplifier – basically a simple differential (transconductance) amplifier – comparing the difference between bit and bit_bar • if bit > bit_bar, output is 1 • if bit < bit_bar, output is 0 • allows output to be set quickly without fully charging/discharging bit line ECE 410, Prof.
    [Show full text]
  • 17. Semiconductor Memories
    17. Semiconductor Memories Institute of Microelectronic Systems Overview •Introduction • Read Only Memory (ROM) • Nonvolatile Read/Write Memory (RWM) • Static Random Access Memory (SRAM) • Dynamic Random Access Memory (DRAM) •Summary Institute of Microelectronic 17: Semiconductor Memories Systems 2 Semiconductor Memory Classification Non-Volatile Memory Volatile Memory Read Only Memory Read/Write Memory Read/Write Memory (ROM) (RWM) Random Non-Random Mask-Programmable EPROM Access Access ROM E2PROM SRAM FIFO Programmable ROM FLASH DRAM LIFO Shift Register EPROM - Erasable Programmable ROM SRAM - Static Random Access Memory E2PROM - Electrically Erasable DRAM - Dynamic Random Access Memory Programmable ROM FIFO - First-In First-Out LIFO - Last-In First-Out Institute of Microelectronic 17: Semiconductor Memories Systems 3 Random Access Memory Array Organization Memory array • Memory storage cells • Address decoders Each memory cell • stores one bit of binary information (”0“ or ”1“ logic) • shares common connections with other cells: rows, columns Institute of Microelectronic 17: Semiconductor Memories Systems 4 Read Only Memory - ROM • Simple combinatorial Boolean network which produces a specific output for each input combination (address) • ”1“ bit stored - absence of an active transistor • ”0“ bit stored - presence of an active transistor • Organized in arrays of 2N words • Typical applications: • store the microcoded instructions set of a microprocessor • store a portion of the operation system for PCs • store the fixed programs for
    [Show full text]
  • A Study About Non-Volatile Memories
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 29 July 2016 doi:10.20944/preprints201607.0093.v1 1 Article 2 A Study about Non‐Volatile Memories 3 Dileep Kumar* 4 Department of Information Media, The University of Suwon, Hwaseong‐Si South Korea ; [email protected] 5 * Correspondence: [email protected] ; Tel.: +82‐31‐229‐8212 6 7 8 Abstract: This paper presents an upcoming nonvolatile memories (NVM) overview. Non‐volatile 9 memory devices are electrically programmable and erasable to store charge in a location within the 10 device and to retain that charge when voltage supply from the device is disconnected. The 11 non‐volatile memory is typically a semiconductor memory comprising thousands of individual 12 transistors configured on a substrate to form a matrix of rows and columns of memory cells. 13 Non‐volatile memories are used in digital computing devices for the storage of data. In this paper 14 we have given introduction including a brief survey on upcoming NVMʹs such as FeRAM, MRAM, 15 CBRAM, PRAM, SONOS, RRAM, Racetrack memory and NRAM. In future Non‐volatile memory 16 may eliminate the need for comparatively slow forms of secondary storage systems, which include 17 hard disks. 18 Keywords: Non‐volatile Memories; NAND Flash Memories; Storage Memories 19 PACS: J0101 20 21 22 1. Introduction 23 Memory is divided into two main parts: volatile and nonvolatile. Volatile memory loses any 24 data when the system is turned off; it requires constant power to remain viable. Most kinds of 25 random access memory (RAM) fall into this category.
    [Show full text]
  • Application Note 63 Using Nonvolatile Static Rams
    APPLICATION NOTE 63 Application Note 63 Using Nonvolatile Static RAMs Vast resources have been expended by the semicon- ability, higher density, low cost, and the ability to be used ductor industry trying to build a nonvolatile random ac- in any semiconductor memory application. cess read/write memory. The effort has been undertak- en because nonvolatile RAM offers several advantages While the various memory components designed to over other memory devices – DRAM, Static RAM, date do not meet the ideal memory scenario, each ex- Shadow RAM, EEPROM, EPROM and ROM – which cels in meeting one or more of the sought after attributes were developed to meet specific applications needs. (Figure 1). Characteristics of the ideal nonvolatile RAM are: low power consumption, higher performance, greater reli- MEMORY ATTRIBUTES Figure 1 EASE OF DATA COST INTERFACE NONVOLATILE DENSITY PERFORMANCE READ/WRITE RETENTION DRAM +++ +++ ++ +++ STATIC RAM +++ + +++ +++ NV SRAM +++ ++ + +++ +++ ++ PARTITIONABLE +++ ++ + +++ +++ ++ NV SRAM PSEUDO STATIC + + ++ + +++ FLASH ++ ++ ++ + ++ + ++ EEPROM + ++ + + + + EPROM ++ ++ ++ ++ + ++ OTP EPROM +++ +++ +++ +++ + +++ ROM +++ +++ +++ +++ + +++ + = Degree of excellence TYPES OF MEMORY ing much more current then an SRAM to maintain the Many types of memories have been devised to meet va- stored data. The net memory cell size is smaller for the rying application needs. However, nonvolatile read/ DRAM than for the SRAM, so the total cost per bit of write random access memories can be substituted for memory is less. The DRAM’s capacitors must be con- all memory types independent of application, if cost is stantly refreshed so that they retain their charge, and re- not a primary consideration. quire more sophisticated interface circuitry. DRAM: Dynamic Random Access Memory.
    [Show full text]
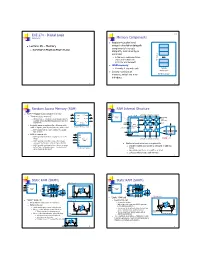
  • ECE 274 - Digital Logic 5.6 Lecture 18 Memory Components
    ECE 274 - Digital Logic 5.6 Lecture 18 Memory Components Register-transfer level Lecture 18 – Memory design instantiates datapath components to create RAM/ROM/EPROM/EEPROM/FLASH datapath, controlled by a controller A few more components are often used outside the M words controller and datapath MxN memory M words, N bits wide each N-bits wide each Several varieties of memory, which we now M×Nmemory introduce 1 2 Random Access Memory (RAM) RAM Internal Structure 32 RAM – Readable and writable memory 32 32 data W_data R_data 10 wdata(N-1) wdata(N-2)wdata0 addr Let A = log2M “Random access memory” 1024x32 4 4 rw bit storage W_addr R_addr RAM word Strange name – Created several decades ago to en enable block d0 (aka “cell”) contrast with sequentially-accessed storage like W_en R_en tape drives 16×32 addr0 a0 word a1 register file addr1 AxM d1 Logically same as register file – Memory with decoder Register file from Chpt. 4 adr address inputs, data inputs/outputs, and control addr(A-1) a(A-1) data cell RAM usually just one port; register file usually word word d(M-1) two or more clk e enableenable 32 rw data RAM vs. register file en data rw to all cells 10 RAM typically larger than roughly 512 or 1024 addr RAM cell words 1024× 32 rdata(N-1) rdata(N-2) rdata0 rw RA M RAM typically stores bits using a bit storage en approach that is more efficient than a flip flop Similar internal structure as register file RAM typically implemented on a chip in a square Decoder enables appropriate word based on address rather than rectangular
    [Show full text]
  • Digital Logic Design Memory and Programmable Logic Devices
    COE 202: Digital Logic Design Memory and Programmable Logic Devices Dr. Ahmad Almulhem Email: ahmadsm AT kfupm Phone: 860-7554 Office: 22-324 Ahmad Almulhem, KFUPM 2010 Memory • Memory: A collection of cells capable of storing binary information (1s or 0s) – in addition to electronic circuit for storing (writing) and retrieving (reading) information. • n data lines (input/output) • k address lines • 2k words (data unit) • Read/Write Control • Memory size = 2k X n Ahmad Almulhem, KFUPM 2010 Memory (cont.) Two Types of Memory: • Random Access Memory (RAM): • Write/Read operations • Volatile: Data is lost when power is turned off • Read Only Memory (ROM): • Read operation (no write) • Non-Volatile: Data is permanent. • PROM is programmable (allow special write) Ahmad Almulhem, KFUPM 2010 Read-Only Memory (ROM) • ROM: A device in which “permanent” binary information is stored using a special device (programmer) k inputs n outputs 2k n ROM (address) x (data) • k inputs (address) 2k words each of size n bits (data) • ROM DOES NOT have a write operation ROM DOES NOT have data inputs Word: group of bits stored in one location Ahmad Almulhem, KFUPM 2010 ROM Internal Logic • The decoder Internal Logic of a 32x8 ROM stage produces ALL possible 0 minterms I0 1 2 • 32 Words of 8 I1 3 5-to-32 . bits each I 2 decoder . 5 input lines . • I3 28 (address) 29 I4 30 • Each OR gate 31 has a 32 input • A contact can be made using fuse/anti-fuse A7 A6 A5 A4 A3 A2 A1 A0 Ahmad Almulhem, KFUPM 2010 Programming a ROM Inputs Outputs I4 I3 I2 I1 I0 A7 A6 A5 A4 A3 A2 A1 A0 x x x x x 0 0 0 0 0 1 0 1 1 0 1 1 0 0 x x x x I0 1 0 0 0 0 1 0 0 0 1 1 1 0 1 x x x x 2 I 0 0 0 1 0 1 1 0 0 0 1 0 1 1 x x x x 3 .
    [Show full text]
  • Semiconductor Memories: Rams and Roms
    Semiconductor Memories: RAMs and ROMs Lesson Objectives: In this lesson you will be introduced to: ¾ Different memory devices like, RAM, ROM, PROM, EPROM, EEPROM, etc. ¾ Different terms like: read, write, access time, nibble, byte, bus, word, word length, address, volatile, non-volatile etc. ¾ How to implement combinational and sequential circuits using ROM. Introduction: The smallest unit of information a digital system can store is a bit, which can be stored in a flip-flop or a 1-bit register. To store m bits of data, an m-bit register with parallel load capability may be used. Data available on the m-bit input lines (I0 to Im-1) may be stored/written into this register under control of the clock by asserting the “Load” control input. The stored m bits of data may be read from the register outputs (O0 to Om-1). The m bits of data stored in a register make up a word. It is simply a number of bits operated upon or considered by the hardware as a group. The number of bits in the word, m, is called word length. The m inputs of the register are provided through an m-bit input data bus and m outputs by an m-bit output data bus. A bus is a number of signal lines, grouped together because of similarity of function, which connect two or more systems or subsystems. A unit of 8-bits of information is referred to as a byte, while 4-bits of information is referred to as a nibble. A memory device can be looked at as consisting of a number of equally sized registers sharing a common set of inputs, and a common set of outputs, as shown in the Figure.
    [Show full text]
  • CMPE-310 Lecture-06: Memory I Outline
    CMPE-310 Lecture-06: Memory I Outline Memory Chips ROM EPROM SRAM DRAM Adapted from lecture notes by Dr Chintan Patel and Avani Dave Memory Chips Memory Types Two basic types: ROM: Read-only memory RAM: Read-Write memory Four commonly used memories: ● ROM ● Flash, EEPROM ● Static RAM (SRAM) ● Dynamic RAM (DRAM), SDRAM, RAMBUS, DDR Adapted from lecture notes by Dr Chintan Patel and Avani Dave Memory Chips Address Pins The number of address pins is related to the number of memory locations. Common sizes today are 1K to 256M locations. Therefore, between 10 and 28 address pins are present. Data Pins The data pins are typically bi-directional in read-write memories. The number of data pins is related to the size of the memory location. For example, an 8-bit wide (byte-wide) memory device has 8 data pins. Catalog listing of 1K X 8 indicate a byte addressable 8K bit memory with 10 address pins. Adapted from lecture notes by Dr Chintan Patel and Avani Dave Memory Chips Control Pins Each memory device has at least one chip select (CS) or chip enable (CE) or select (S) pin that enables the memory device. This enables read and/or write operations. If more than one are present, then all must be 0 in order to perform a read or write. Each memory device has at least one control pin. For ROMs, an output enable (OE) or gate (G) is present. The OE pin enables and disables a set of tristate buffers. For RAMs, a read-write (R/W) or write enable (WE) and read enable (OE) are present.
    [Show full text]