Towers on the Moon: 1. Concrete
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Copyrighted Material
Index Abulfeda crater chain (Moon), 97 Aphrodite Terra (Venus), 142, 143, 144, 145, 146 Acheron Fossae (Mars), 165 Apohele asteroids, 353–354 Achilles asteroids, 351 Apollinaris Patera (Mars), 168 achondrite meteorites, 360 Apollo asteroids, 346, 353, 354, 361, 371 Acidalia Planitia (Mars), 164 Apollo program, 86, 96, 97, 101, 102, 108–109, 110, 361 Adams, John Couch, 298 Apollo 8, 96 Adonis, 371 Apollo 11, 94, 110 Adrastea, 238, 241 Apollo 12, 96, 110 Aegaeon, 263 Apollo 14, 93, 110 Africa, 63, 73, 143 Apollo 15, 100, 103, 104, 110 Akatsuki spacecraft (see Venus Climate Orbiter) Apollo 16, 59, 96, 102, 103, 110 Akna Montes (Venus), 142 Apollo 17, 95, 99, 100, 102, 103, 110 Alabama, 62 Apollodorus crater (Mercury), 127 Alba Patera (Mars), 167 Apollo Lunar Surface Experiments Package (ALSEP), 110 Aldrin, Edwin (Buzz), 94 Apophis, 354, 355 Alexandria, 69 Appalachian mountains (Earth), 74, 270 Alfvén, Hannes, 35 Aqua, 56 Alfvén waves, 35–36, 43, 49 Arabia Terra (Mars), 177, 191, 200 Algeria, 358 arachnoids (see Venus) ALH 84001, 201, 204–205 Archimedes crater (Moon), 93, 106 Allan Hills, 109, 201 Arctic, 62, 67, 84, 186, 229 Allende meteorite, 359, 360 Arden Corona (Miranda), 291 Allen Telescope Array, 409 Arecibo Observatory, 114, 144, 341, 379, 380, 408, 409 Alpha Regio (Venus), 144, 148, 149 Ares Vallis (Mars), 179, 180, 199 Alphonsus crater (Moon), 99, 102 Argentina, 408 Alps (Moon), 93 Argyre Basin (Mars), 161, 162, 163, 166, 186 Amalthea, 236–237, 238, 239, 241 Ariadaeus Rille (Moon), 100, 102 Amazonis Planitia (Mars), 161 COPYRIGHTED -

2021 Transpacific Yacht Race Event Program
TRANSPACTHE FIFTY-FIRST RACE FROM LOS ANGELES 2021 TO HONOLULU 2 0 21 JULY 13-30, 2021 Comanche: © Sharon Green / Ultimate Sailing COMANCHE Taxi Dancer: © Ronnie Simpson / Ultimate Sailing • Hamachi: © Team Hamachi HAMACHI 2019 FIRST TO FINISH Official race guide - $5.00 2019 OVERALL CORRECTED TIME WINNER P: 808.845.6465 [email protected] F: 808.841.6610 OFFICIAL HANDBOOK OF THE 51ST TRANSPACIFIC YACHT RACE The Transpac 2021 Official Race Handbook is published for the Honolulu Committee of the Transpacific Yacht Club by Roth Communications, 2040 Alewa Drive, Honolulu, HI 96817 USA (808) 595-4124 [email protected] Publisher .............................................Michael J. Roth Roth Communications Editor .............................................. Ray Pendleton, Kim Ickler Contributing Writers .................... Dobbs Davis, Stan Honey, Ray Pendleton Contributing Photographers ...... Sharon Green/ultimatesailingcom, Ronnie Simpson/ultimatesailing.com, Todd Rasmussen, Betsy Crowfoot Senescu/ultimatesailing.com, Walter Cooper/ ultimatesailing.com, Lauren Easley - Leialoha Creative, Joyce Riley, Geri Conser, Emma Deardorff, Rachel Rosales, Phil Uhl, David Livingston, Pam Davis, Brian Farr Designer ........................................ Leslie Johnson Design On the Cover: CONTENTS Taxi Dancer R/P 70 Yabsley/Compton 2019 1st Div. 2 Sleds ET: 8:06:43:22 CT: 08:23:09:26 Schedule of Events . 3 Photo: Ronnie Simpson / ultimatesailing.com Welcome from the Governor of Hawaii . 8 Inset left: Welcome from the Mayor of Honolulu . 9 Comanche Verdier/VPLP 100 Jim Cooney & Samantha Grant Welcome from the Mayor of Long Beach . 9 2019 Barndoor Winner - First to Finish Overall: ET: 5:11:14:05 Welcome from the Transpacific Yacht Club Commodore . 10 Photo: Sharon Green / ultimatesailingcom Welcome from the Honolulu Committee Chair . 10 Inset right: Welcome from the Sponsoring Yacht Clubs . -

March 21–25, 2016
FORTY-SEVENTH LUNAR AND PLANETARY SCIENCE CONFERENCE PROGRAM OF TECHNICAL SESSIONS MARCH 21–25, 2016 The Woodlands Waterway Marriott Hotel and Convention Center The Woodlands, Texas INSTITUTIONAL SUPPORT Universities Space Research Association Lunar and Planetary Institute National Aeronautics and Space Administration CONFERENCE CO-CHAIRS Stephen Mackwell, Lunar and Planetary Institute Eileen Stansbery, NASA Johnson Space Center PROGRAM COMMITTEE CHAIRS David Draper, NASA Johnson Space Center Walter Kiefer, Lunar and Planetary Institute PROGRAM COMMITTEE P. Doug Archer, NASA Johnson Space Center Nicolas LeCorvec, Lunar and Planetary Institute Katherine Bermingham, University of Maryland Yo Matsubara, Smithsonian Institute Janice Bishop, SETI and NASA Ames Research Center Francis McCubbin, NASA Johnson Space Center Jeremy Boyce, University of California, Los Angeles Andrew Needham, Carnegie Institution of Washington Lisa Danielson, NASA Johnson Space Center Lan-Anh Nguyen, NASA Johnson Space Center Deepak Dhingra, University of Idaho Paul Niles, NASA Johnson Space Center Stephen Elardo, Carnegie Institution of Washington Dorothy Oehler, NASA Johnson Space Center Marc Fries, NASA Johnson Space Center D. Alex Patthoff, Jet Propulsion Laboratory Cyrena Goodrich, Lunar and Planetary Institute Elizabeth Rampe, Aerodyne Industries, Jacobs JETS at John Gruener, NASA Johnson Space Center NASA Johnson Space Center Justin Hagerty, U.S. Geological Survey Carol Raymond, Jet Propulsion Laboratory Lindsay Hays, Jet Propulsion Laboratory Paul Schenk, -
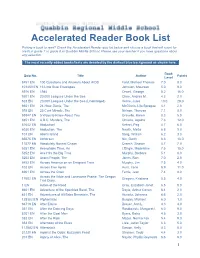
Accelerated Reader Book List
Accelerated Reader Book List Picking a book to read? Check the Accelerated Reader quiz list below and choose a book that will count for credit in grade 7 or grade 8 at Quabbin Middle School. Please see your teacher if you have questions about any selection. The most recently added books/tests are denoted by the darkest blue background as shown here. Book Quiz No. Title Author Points Level 8451 EN 100 Questions and Answers About AIDS Ford, Michael Thomas 7.0 8.0 101453 EN 13 Little Blue Envelopes Johnson, Maureen 5.0 9.0 5976 EN 1984 Orwell, George 8.2 16.0 9201 EN 20,000 Leagues Under the Sea Clare, Andrea M. 4.3 2.0 523 EN 20,000 Leagues Under the Sea (Unabridged) Verne, Jules 10.0 28.0 6651 EN 24-Hour Genie, The McGinnis, Lila Sprague 4.1 2.0 593 EN 25 Cent Miracle, The Nelson, Theresa 7.1 8.0 59347 EN 5 Ways to Know About You Gravelle, Karen 8.3 5.0 8851 EN A.B.C. Murders, The Christie, Agatha 7.6 12.0 81642 EN Abduction! Kehret, Peg 4.7 6.0 6030 EN Abduction, The Newth, Mette 6.8 9.0 101 EN Abel's Island Steig, William 6.2 3.0 65575 EN Abhorsen Nix, Garth 6.6 16.0 11577 EN Absolutely Normal Chaos Creech, Sharon 4.7 7.0 5251 EN Acceptable Time, An L'Engle, Madeleine 7.5 15.0 5252 EN Ace Hits the Big Time Murphy, Barbara 5.1 6.0 5253 EN Acorn People, The Jones, Ron 7.0 2.0 8452 EN Across America on an Emigrant Train Murphy, Jim 7.5 4.0 102 EN Across Five Aprils Hunt, Irene 8.9 11.0 6901 EN Across the Grain Ferris, Jean 7.4 8.0 Across the Wide and Lonesome Prairie: The Oregon 17602 EN Gregory, Kristiana 5.5 4.0 Trail Diary.. -

20-1265 Transfer of Unclaimed Property Funds from Their
Board Office Use: Legislative File Info. File ID Number 20-1265 Introduction Date 8/12/2020 REVISED - BOARD PUBLIC SESSION - 8/12/2020 Enactment Number 20-1156 Enactment Date 8/12/2020 os Memo To Board of Education From Kyla Johnson-Trammell, Superintendent Lisa Grant-Dawson, Chief Business Officer Ryan Nguyen, Controller Board Meeting Date August 12, 2020 Subject Transfer of Funds from the Unclaimed Property from Respective Fund(s) to General Fund - Fiscal Year 2019-2020 Action Requested Approval by the Board of Education of Resolution No. 2021-0009 for the Transferring of Funds from the Unclaimed Stale Dated Warrants that are past three (3) years from the issuance date, to the General Fund as allowed by California Government Codes Sections 50005-20057 on unclaimed property. For Fiscal Year 2019-20, the unclaimed stale dated warrants, which can be transferred to the General Fund, account for 2,680 items and amount to $1,069,434.46 as reflected in EXHIBIT A. Background As recommended by the District’s External Auditor, the District must maintain an accurate and up-to-date listing of stale dated warrants readily available for the rightful owner to file a claim. The District’s staff checked the California Laws and State Controller’s guidance on unclaimed property and developed the Stale Warrants Policy and Procedures (EXHIBIT B). Such policy and procedures were approved by the General Counsel Office on May 20th, 2020. The District must follow steps outlined in the District’s approved Stale Warrant Policy and Procedures, which include serving the public notice in the local newspaper and obtaining Board’s approval prior transferring the unclaimed funds to the General Fund for general purposes. -

On the Effect of Magnetospheric Shielding on the Lunar Hydrogen Cycle O
On the Effect of Magnetospheric Shielding on the Lunar Hydrogen Cycle O. J. Tucker1*, W. M. Farrell1, and A. R. Poppe2 1NASA Goddard Space Flight Center, Greenbelt, Md, USA. 2Space Sciences Laboratory, University of California, Berkeley, CA, USA *Corresponding author: Orenthal Tucker ([email protected]) NASA Goddard Space Flight Center, Magnetospheric Physics/Code 695, Greenbelt, MD 20771, USA Key Points: Low latitude nightside OH is depleted from waning gibbous to waxing crescent because of shielding when traversing the magnetotail. Low latitude dayside OH is decreased in the tail compared to out but the difference cannot be resolved with current observations. Magnetospheric shielding decreases the global H2 exosphere by an order of magnitude during the full Moon. 1 Abstract The global distribution of surficial hydroxyl on the Moon is hypothesized to be derived from the implantation of solar wind protons. As the Moon traverses the geomagnetic tail it is generally shielded from the solar wind, therefore the concentration of hydrogen is expected to decrease during full Moon. A Monte Carlo approach is used to model the diffusion of implanted hydrogen atoms in the regolith as they form metastable bonds with O atoms, and the subsequent degassing of H2 into the exosphere. We quantify the expected change in the surface OH and the H2 exosphere using averaged SW proton flux obtained from the Acceleration, Reconnection, Turbulence, and Electrodynamics of the Moon’s Interaction with the Sun (ARTEMIS) measurements. At lunar local noon there is a small difference less than ~10 ppm between the surface concentrations in the tail compared to out. -

Official 2019 Half Marathon Results Book
OFFICIAL RESULTS BOOK November 8-10, 2019 2019 Official Race Results 3 Thanks For Your Participation 4 Elite Review 6 Event Statistics 7 Ad-Merchandise Blowout Sale 8 Half Marathon Finisher & Divisional Winners - Male 9 Half Marathon Overall Results - Male 20 Half Marathon Finisher & Divisional Winners - Female 21 Half Marathon Overall Results - Female 39 By-the-Bay 3K & Pacific Grove Lighthouse 5K 40 5K Divisional Results - Male & Female 41 5K Overall Results - Male 44 5K Overall Results - Female 48 3K Results (alphabetical) 50 Half Marathon Memories 51 Our Volunteers 52 Our Sponsors & Supporters 53 Our Family of Events MONTEREYBAYHALFMARATHON.ORG P.O. Box 222620 Carmel, CA 93922-2620 831.625.6226 [email protected] A Big Sur Marathon Foundation Event James Short Cover photo by Andrew Tronick Thanks For Your Participation Thank you for your participation in the Monterey the Name of Love in June and the year-round Bay Half Marathon weekend of events! JUST RUN® youth fitness program. Our mission is to create beautiful events that promote health and We were so happy to host you this year. After the benefit the community. Each year, our organization cancellation of the Half Marathon in 2018, it was distributes more than $400,000 in grants to other great to finally see the streets of Monterey and non-profit organizations and agencies. Your entry Pacific Grove filled with runners. The conditions for fees and support of our events makes this possible. the Saturday and Sunday races were excellent and we know many of you ran personal bests on our The race wouldn’t happen without our dedicated scenic courses. -

Natural Thermoluminescence of Lunar Samples
52nd Lunar and Planetary Science Conference 2021 (LPI Contrib. No. 2548) 2658.pdf NATURAL THERMOLUMESCENCE OF LUNAR SAMPLES: REVIEW AND UPDATE. A. Sehlke1, D. W. G. Sears1 and the ANGSA Science Team. 1NASA Ames Research Center/ Bay Area Environmental Research Institute, Moffett Field, CA 94035, USA, [email protected]. Introduction: Thermoluminescence (TL), literally TL measurements, the sample may not be exposed to light emission caused by heating, is a widely used and any ionizing radiation or other light sources (such as widely studied process in dosimetry, dating and various fluorescent light bulbs) after it has been removed from industries. Ionizing radiations passing through its sampling location, because this artificial radiation crystalline materials cause electrons to be energized and exposure can provide enough energy to reconfigure “trapped” where they can be stable for minutes to trapped electrons (excitation and drainage). billions of years [1]. Heat provides the energy for the Applications For Natural TL Measurements: electrons to fall back to their low energy ground states, Transient Lunar Phenomenon. Interest in TL releasing the excess energy as light. The number and measurements on lunar surface materials was prompted energy level of trapped electrons is a balance between in some part by the observations of light being emitted the radiation environment (i.e., the dose of ionizing by the lunar surface, the so-called “transient lunar radiation absorbed) vs. the thermal environment (i.e., phenomenon” (TLP) [8]. It was quickly realized that storage temperature of the sample), as well as the sample luminescence was not efficient enough to petrology of the sample (i.e., type of crystal lattice and explain the TLP and interest turned to using TL to defects). -

Iaa Commission Iii Sg 2 – Nuclear Space Power and Propulsion
IAA COMMISSION III SG 2 – NUCLEAR SPACE POWER AND PROPULSION M. Auweter-Kurtz C. Bruno D. Fearn H. Kurtz T.J. Lawrence R.X. Lenard List of contents Introduction 8 1. Physics of Nuclear Propulsion – An Introduction 11 1.1. ABSTRACT 11 1.2. Introduction 11 1.3. Fundamental Physics 12 1.3.1. Forces 12 1.4. Propulsion 19 1.4.3. Power 23 1.4.4. Mass 25 1.5. Nuclear Propulsion Strategies 27 1.5.1. Nuclear Thermal Rockets (NTR) 27 1.5.2. Nuclear Electric Propulsion (NEP) 31 1.5.3. A Comparison between Chemical and NTR/NEP Isp 32 1.6. Massless (Photonic) Propulsion 33 1.7. Conclusions 34 1.8. References 35 2. Nulcear Thermal Rocket Propulsion Systems 38 2.1. ABSTRACT 38 2.2. Introduction 38 2.3. System Configuration and Operation 41 2.4. Particle-Bed Reactor 46 2.4.1. CERMET 47 2.5. Safety 49 2.6. MagOrion and Mini-MagOrion 51 2.7. Conclusions 53 2.8. References 54 3. The application of ion thrusters to high thrust, high specific impulse nuclear-electric missions 57 3.1. ABSTRACT 57 3.2. Introduction 60 3.3. Background 62 3.3.1. Space Nuclear Programmes 62 2 3.3.2. Advantages of Electric Propulsion 63 3.3.3. Propulsion System Parameters 64 3.3.4. Propulsion Technology Review 66 3.3.4.1. Gridded Ion Engines 66 3.3.4.2. The Hall-Effect Thruster 69 3.3.4.3. Magnetoplasmadynamic (MPD) Thrusters 71 3.3.4.4. Variable Specific Impulse Magnetoplasma Rocket (VASIMR) 72 3.4. -

Circumnavigation of Sicily
Circumnavigation of Sicily September 26 - October 8, 2017 Wednesday & Thursday, September 27 & 28, 2017 Valletta, Malta / Embark Variety Voyager Welcome to Malta! The beautiful blue skies and sun-warmed streets of the honey-colored sandstone—for which the island was named—encouraged some of us to sip on a cappuccino in a sidewalk café, while more energetic souls explored the ramparts, monuments, and shops of Valletta. We assembled in the evening at the Grand Hotel Excelsior to meet our fellow adventurers and the Expedition Staff over cocktails and dinner. As night fell, we became acquainted with our new companions, compared notes on previous trips, and discussed each other’s anticipated highlights of the upcoming days. Our adventure began in earnest this morning as we started the day winding our way through a patchwork of small farms separated by dry stone walls. After a short stop at the azure waters of the Blue Grotto, with its photogenic stone arches, we reached the megalithic site of Hagar Qim perched on a bluff overlooking the Mediterranean Sea. Dated between 3000 and 2500 BC, this is the oldest structure on Malta and one of the oldest structures in the world, as well as a UNESCO World Heritage Site. Returning to the capital city of Valletta, we visited the National Museum of Archaeology to view, among other artifacts, the exquisite Sleeping Lady, the fertility figure from the third millennium BC. The Grand Master’s Palace of the Knights of Malta kept our heads turning, from its walls and ceilings painted with historic figures to the stone marquetry underfoot. -

Seismological Monitoring of the World's First
Appendix A Seismological Monitoring of the World’s First Nuclear Detonation— The Trinity Shot of 16 July 19451 Seismology played a modest role in the Trinity test, thereby establishing, at the very birth of the “atomic age,” a mutual interaction between seismology and nuclear testing that would become of increasing significance to both technologies as the century pro- gressed. Because the Trinity “gadget” was designed to be an atmospherically detonated military weapon for which principal damage effects were expected to be air blast and accompanying ground shock of intensities heretofore unexplored, extensive new effects data were needed to plan military applications. When the need for a full-scale test of the implosion design became clear by late 1944, Los Alamos scientists began to devise field experiments to measure both air blast and ground shock.Also, they wanted to esti- mate how each would scale with explosive energy release (yield), range, and height of burst within a principal target area (nominally, within about 20 km of ground zero). In March 1945, Herbert M. Houghton, an exploration geophysicist with Geophys- ical Research Corporation (GRC) and Tidewater Oil, was recruited to work with Los Alamos physicist, James Coon, to perfect earth shock instrumentation for the 100-ton TNT calibration rehearsal shot of 7 May 1945, as well as the unique multikiloton Trin- ity nuclear event planned for July. Houghton and Coon modified a dozen GRC Type SG-3 geophones to record both vertical and horizontal-radial components of strong ground motion at ranges between 0.75 and 8.2 km from both the calibration and nuclear shots, which were air bursts suspended on towers. -

PREM-DISSERTATION-2017.Pdf
Copyright by Parvathy Prem 2017 The Dissertation Committee for Parvathy Prem certifies that this is the approved version of the following dissertation: DSMC Simulations of Volatile Transport in a Transient Lunar Atmosphere and Ice Deposition in Cold Traps after a Comet Impact Committee: David B. Goldstein, Supervisor Philip L. Varghese, Co-Supervisor Laurence M. Trafton, Co-Supervisor Laxminarayan L. Raja Richard C. Elphic DSMC Simulations of Volatile Transport in a Transient Lunar Atmosphere and Ice Deposition in Cold Traps after a Comet Impact by Parvathy Prem, BE; MSE Dissertation Presented to the Faculty of the Graduate School of The University of Texas at Austin in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy The University of Texas at Austin May 2017 Epigraph “All that survives after our death are publications and people. So look carefully after the words you write, the thoughts and publications you create, and how you love others. For these are the only things that will remain.” – Susan Niebur (1973-2012) Acknowledgements First and foremost, I would like to thank my advisors – Prof. David Goldstein, Prof. Philip Varghese and Dr. Laurence Trafton – for their guidance, encouragement and support over almost seven years of graduate study. They have my gratitude and respect not only for their (willingly shared) scientific expertise, but also for the high standards to which they hold their work (and that of their students), for the balance of guidance and independence that they provide as advisors, and for the consideration with which they treat others. One of the main reasons I wished to complete this PhD was to be able to pay forward what I’ve gained from their training; I would be more than satisfied if I could ever advise a student even half as well as they have.