DOCSLIB.ORG

Absorbed Dose in Radioactive Media Outline Introduction Radiation Equilibrium Charged-Particle Equilibrium Limiting Cases

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Absorbed Dose in Radioactive Media Outline Introduction Radiation Equilibrium Charged-Particle Equilibrium Limiting Cases Outline • General dose calculation considerations, Absorbed Dose in Radioactive absorbed fraction Media • Radioactive disintegration processes and associated dose deposition – Alpha disintegration Chapter 5 – Beta disintegration – Electron-capture transitions F.A. Attix, Introduction to Radiological – Internal conversion Physics and Radiation Dosimetry • Summary Introduction Radiation equilibrium • We are interested in calculating the absorbed dose in a. The atomic composition radioactive media, applicable to cases of of the medium is – Dose within a radioactive organ homogeneous – Dose in one organ due to radioactive source in another b. The density of the organ medium is • If conditions of CPE or RE are satisfied, dose homogeneous c. The radioactive source calculation is straightforward is uniformly distributed • Intermediate situation is more difficult but can be d. No external electric or handled at least in approximations magnetic fields are present Charged-particle equilibrium Limiting cases • Emitted radiation typically includes both • Each charged particle of a given type and photons (longer range) and charged energy leaving the volume is replaced by an particles (shorter range) identical particle of the same energy entering • Assume the conditions for RE are satisfied the volume • Consider two • Existence of RE is sufficient condition for CPE limited cases based • Even if RE does not exist CPE may still exist on the size of the (for a very large or a very small volume) radioactive object 1 Limiting cases: small object Limiting cases: large object • A radioactive object V having a mean radius not much • A radioactive object V with mean radius » l/m for greater than the maximum charged-particle range d the most penetrating g-rays • CPE is well approximated at any internal point P that is at least a distance d from the boundary of V • RE is well approximated at any internal point P • If d« l/m for the g-rays, the absorbed dose D at P that is far enough from the boundary of V so g-ray approximately equals to the energy per unit mass of penetration through that distance is negligible medium that is given to the charged particles in radioactive decay (less their radiative losses) • The dose at P will then equal the sum of the • The photons escape from the object and are assumed not energy per unit mass of medium that is given to to be scattered back by its surroundings charged particles plus g-rays in radioactive decay Limiting cases: large object Absorbed fraction • Deciding upon a maximum • An intermediate-size radioactive object V g-ray “range” L for this case requires quantitative • Dose at P will then equal the sum of the energy criterion per unit mass of medium that is given to – For primary beam only (m) the charged particles plus dose from some g-rays penetration is < 0.1% through L~7 mean free paths • To estimate the dose from g-rays define – Taking into account scatter, absorbed fraction: (broad beam geometry, m ) g - ray radiant energy absorbed in target volume will increase the required AF object size to satisfy the g - ray radiant energy emitted by source attenuation objectives Attenuation of 1MeV g-rays in water Intermediate-size radioactive object Case 1 • Reciprocity theorem: energy spent • Consider volume V filled by a homogeneous medium and a in dv due to the source in dv’: uniformly distributed g-source d v ,dv dv ,d v and dv ,V V ,dv • The volume may be surrounded by • No source in dv” Case 1: infinite homogeneous medium identical to V, but non- • Define Rdv as the expectation radioactive (an organ in the value of the g-ray radiant energy body) emitted by the source in dv, and Case 2: infinite vacuum (object in dv,V the part of that energy that is air) spent in V (source dv and target V) 2 Case 1 continued Case 1 continued • The absorbed fraction with respect • Reduction in the absorbed dose due to g-rays to source dv and target V is : energy escaping from V • Can estimate AF using mean effective attenuation dv ,V V ,dv AF dv ,V coefficient for g-rays energy fluence through a R dv R dv distance r in the medium source, target 2 • Estimates reduction in absorbed 1 m r AF 1 e sin d d dv ,V dose relative to RE condition 4 • For very small radioactive objects 0 0 (V dv) this absorbed fraction • For poly-energetic sources have to find an average approaches zero; for an infinite value of the absorbed fraction radioactive medium it equals unity Case 1 example Case 2 Radioactive object V surrounded by vacuum • More difficult to calculate radius of sphere • The reciprocity theorem is only approximate due to the lack of backscattering • Energy dependence (max ~80keV) • Dose is lower than in Case 1 (ratios >1) m • Dose calculations published in MIRD (Medical Internal Radiation Dosimetry) reports • The larger the radius, the lower the g-ray energy – the closer to RE condition (AF=1) Case 2 MIRD tables Pamphlet 11, 1975 • To obtain a crude estimate of the dose at some • AF is incorporated in “S-value” point P within a uniformly g-active homogeneous tabulated for each radionuclide object, it may suffice to obtain the average and source-target configuration distance r from the point to the surface of the used in nuclear medicine object by • Dose absorbed in any organ Pamphlet 1 2 (target) due to a source in some r r sin d d other organ is calculated based 5rev, 1978 4 0 0 on cumulative activity, D=AxS • Then one may employ men = m in the straight- • S values are typically calculated ahead approximation to obtain by Monte Carlo technique • Straightforward approach, but m en r AF dv ,V 1 e accuracy is limited 3 MIRD tables MIRD tables Bouchet et al., MIRD Pamphlet No. 19, The Journal of Nuc. Med., Vol. 44, p. 1113, 2003 • The accuracy is continuously improved through revisions and updates • Example: kidneys represent a frequent source of radiopharmaceutical uptake in both diagnostic and therapeutic nuclear medicine Bouchet et al., MIRD Pamphlet No. 19, THE JOURNAL OF NUC. MED., Vol. 44, p. 1113, 2003 Radioactive disintegration processes Alpha disintegration • Radioactive nuclei undergo transformations to a more stable state through expulsion of energetic particles • Occurs mainly in heavy nuclei • Example: decay of radium to radon, presented by the mass-energy balance equation 226 222 4 • The total mass, energy, momentum, and electric 88 Ra 86 Rn 2 He 4 .78 MeV 1602 y charge are conserved parent 1 / 2 daughter • Energy equivalent of the rest mass: • Each of the elemental terms represents the rest 12 mass of a neutral atom of that element – 1 amu=1/12 of the mass of 6C nucleus=931.50 MeV – 1 electron mass=0.51100 MeV • Energy term represents kinetic energy released Absorbed dose from Alpha disintegration - disintegration • Take into account both branches through the average branching ratios • For radium average kinetic energy given to charged particles per disintegration E 0 .946 4 .78 MeV 0.054 4.6 MeV 4.77 MeV • For CPE condition in a small (1 cm) radium-activated object: D=4.77 x n MeV/g, where n – number of • Two branches are available for disintegration disintegrations per gram of the matter • Kinetic + quantum energy released is 4.78MeV • For RE condition (large object): D=4.78 x n MeV/g, • After the -particle slows down it captures two electrons from includes g-ray energy its surroundings, becoming a neutral He atom 4 Beta disintegration Beta disintegration • Nuclei having excess of neutrons typically emit an electron, - particle; atomic number Z is increased by 1 • Nuclei having excess of protons typically emit positron, + particle; atomic number Z is decreased by 1 • Nucleus is left in an exited state, emitting one or more g-rays • Example: 32 32 - 0 • Kinetic energy 1.71 MeV is shared between - and neutrino 15 P 16 S 0 1 .71 MeV 1 / 2 14 .3 d 32 + kinetic energy • Charge balance is realized through initially ion of 16S capturing an electron Beta disintegration Beta disintegration • Average kinetic energy of the - or + particle is typically • In + disintegration valence electron is emitted simultaneously 0.3-0.4 Emax; 1/3 Emax is often used for purposes of roughly 15 15 estimating absorbed dose • Example: 8O -> 7N 15 15 - 0 • Neutrino is not included in dose estimates due to almost zero 8 O 7 N e 0 1 .73 MeV 122 s rest mass energy and no charge 1 / 2 2 positron annihilation yields 2m0c =1.022 MeV Absorbed dose from Example 5.1 - disintegration • Uniformly distributed - and g-ray source • The rest-mass loss is spent • Under CPE condition D=nEavg MeV/g for n – half in 1 -MeV g -ray production and disintegrations per gram of medium - – half in -decay, for which Emax=5 MeV and Eavg=2 MeV • Any additional contributions to energy • The point of interest P is located >5 cm inside_ the deposition due to g-rays must be included boundary of the object, at an average distance r = 20 for RE condition cm from the boundary. -1 -1 • Radiative losses by -rays, such as • men=0.0306 cm and m = 0.0699 cm for the g -rays bremsstrahlung and in-flight annihilation, • A total energy of 10-2 J converted from rest mass in are ignored each kg of the object • Estimate the absorbed dose at P 5 Example 5.1 Example 5.2 • For -ray Emax=5 MeV corresponds to maximum particle range (Appendix E) d ~2.6 cm << 1/m=14.3 cm • CPE exists at P, therefore dose due to -rays: • What is the absorbed dose rate (Gy/h) at the 1 2 2 center of a sphere of water 1 cm in radius, D E avg 10 J/kg 10 J/kg 2 32 homogeneously radioactivated by 15P, 1/m • For g-ray 20cm is not >> 1/m=14.3
Load more

Recommended publications
  • Development of Chemical Dosimeters Development Of
    SUDANSUDAN ACADEMYAGADEMY OFOF SCIENCES(SAS)SGIENGES(SAS) ATOMICATOMIC ENERGYEhTERGYRESEARCHESRESEARCHES COORDINATIONCOORDII\rATI ON COUNCILCOUNCIL - Development of Chemical Dosimeters A dissertation Submitted in a partial Fulfillment of the Requirement forfbr Diploma Degree in Nuclear Science (Chemistry) By FareedFadl Alla MersaniMergani SupervisorDr K.S.Adam MurchMarch 2006 J - - - CONTENTS Subject Page -I - DedicationDedication........ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... I Acknowledgement ... '" ... ... ... ... ... ... '" ... ... ... ... '" ... '" ....... .. 11II Abstract ... ... ... '" ... ... ... '" ... ... ... ... -..... ... ... ... ... ... ..... III -I Ch-lch-1 DosimetryDosimefry - 1-1t-l IntroductionLntroduction . 1I - 1-2t-2 Principle of Dosimetry '" '" . 2 1-3l-3 DosimetryDosimefiySystems . 3J 1-3-1l-3-l primary standard dosimeters '" . 4 - 1-3-2l-3-Z Reference standard dosimeters ... .. " . 4 1-3-3L-3-3 Transfer standard dosimeters ... ... '" . 4 1-3-4t-3-4 Routine dosimeters . 5 1-4I-4 Measurement of absorbed dose . 6 1-5l-5 Calibration of DosimetryDosimetrvsystemsvstem '" . 6 1-6l-6 Transit dose effects . 8 Ch-2ch-2 Requirements of chemical dosimeters 2-12-l Introduction ... ... ... .............................................. 111l 2-2 Developing of chemical dosimeters ... ... .. ....... ... .. ..... 12t2 2-3 Classification of Dosimetry methods.methods .......................... 14l4 2-4 RequirementsRequiremsnts of ideal chemical dosimeters ,. ... 15 2-5 Types of chemical system .
    [Show full text]
  • The International Commission on Radiological Protection: Historical Overview
    Topical report The International Commission on Radiological Protection: Historical overview The ICRP is revising its basic recommendations by Dr H. Smith Within a few weeks of Roentgen's discovery of gamma rays; 1.5 roentgen per working week for radia- X-rays, the potential of the technique for diagnosing tion, affecting only superficial tissues; and 0.03 roentgen fractures became apparent, but acute adverse effects per working week for neutrons. (such as hair loss, erythema, and dermatitis) made hospital personnel aware of the need to avoid over- Recommendations in the 1950s exposure. Similar undesirable acute effects were By then, it was accepted that the roentgen was reported shortly after the discovery of radium and its inappropriate as a measure of exposure. In 1953, the medical applications. Notwithstanding these observa- ICRU recommended that limits of exposure should be tions, protection of staff exposed to X-rays and gamma based on consideration of the energy absorbed in tissues rays from radium was poorly co-ordinated. and introduced the rad (radiation absorbed dose) as a The British X-ray and Radium Protection Committee unit of absorbed dose (that is, energy imparted by radia- and the American Roentgen Ray Society proposed tion to a unit mass of tissue). In 1954, the ICRP general radiation protection recommendations in the introduced the rem (roentgen equivalent man) as a unit early 1920s. In 1925, at the First International Congress of absorbed dose weighted for the way different types of of Radiology, the need for quantifying exposure was radiation distribute energy in tissue (called the dose recognized. As a result, in 1928 the roentgen was equivalent in 1966).
    [Show full text]
  • Radiation Glossary
    Radiation Glossary Activity The rate of disintegration (transformation) or decay of radioactive material. The units of activity are Curie (Ci) and the Becquerel (Bq). Agreement State Any state with which the U.S. Nuclear Regulatory Commission has entered into an effective agreement under subsection 274b. of the Atomic Energy Act of 1954, as amended. Under the agreement, the state regulates the use of by-product, source, and small quantities of special nuclear material within said state. Airborne Radioactive Material Radioactive material dispersed in the air in the form of dusts, fumes, particulates, mists, vapors, or gases. ALARA Acronym for "As Low As Reasonably Achievable". Making every reasonable effort to maintain exposures to ionizing radiation as far below the dose limits as practical, consistent with the purpose for which the licensed activity is undertaken. It takes into account the state of technology, the economics of improvements in relation to state of technology, the economics of improvements in relation to benefits to the public health and safety, societal and socioeconomic considerations, and in relation to utilization of radioactive materials and licensed materials in the public interest. Alpha Particle A positively charged particle ejected spontaneously from the nuclei of some radioactive elements. It is identical to a helium nucleus, with a mass number of 4 and a charge of +2. Annual Limit on Intake (ALI) Annual intake of a given radionuclide by "Reference Man" which would result in either a committed effective dose equivalent of 5 rems or a committed dose equivalent of 50 rems to an organ or tissue. Attenuation The process by which radiation is reduced in intensity when passing through some material.
    [Show full text]
  • Emergency and Combat First Aid» Module № 1 Emergency and Combat First Aid Topic 7 Means of Mass Destruction
    Ministry of Health of Ukraine Ukrainian Medical stomatological Academy It is ratified On meeting department Of accident aid and military medicine «___»_____________20 __y. Protocol №_____ Manager of department DMSc ., assistant professor __________К.Shepitko METHODICAL INSTRUCTION FOR INDEPENDENT WORK OF STUDENTS DURING PREPARATIONS FOR THE PRACTICAL LESSON Educational discipline «Emergency and Combat First Aid» Module № 1 Emergency and Combat First Aid Topic 7 Means of Mass Destruction. First Aid. Weapons of mass destructions. Lesson 10 Radiations chemical accidents .First Aid Сourse ІІ Foreing students training dentistry Faculty Training of specialists of the second (master) level of higher of education (название уровня высшего образования) Areas of knowledge _______ 22 «Health protection»_________ (шифр и название области знаний) Specialty ________222 «Medicine», 221 «Stomatology»________________ (код и наименование специальности) Poltava 2019 The relevance of the topic: Military action in modern warfare will be carried out with high activity and limit tension. They cause great losses in the army and among the population, the destruction of potentially dangerous objects, energy centers, waterworks, the formation of large zones of destruction, fires and floods. The main form of countering in the war, is armed struggle - the organized use of armed forces and weapons to achieve specific political and military objectives, a combination of military actions of varying scales. To conventional weapons, the application of which may cause losses among the population are missiles and aerial munitions, including precision munitions volumetric detonation of cluster and incendiary. Have the greatest efficiency high precision conventional weapons, which provide automatic detection and reliable destruction of targets and enemy targets with a single shot (trigger).
    [Show full text]
  • 11. Dosimetry Fundamentals
    Outline • Introduction Dosimetry Fundamentals • Dosimeter model • Interpretation of dosimeter measurements Chapter 11 – Photons and neutrons – Charged particles • General characteristics of dosimeters F.A. Attix, Introduction to Radiological Physics and Radiation Dosimetry • Summary Introduction Dosimeter • Radiation dosimetry deals with the determination • A dosimeter can be generally defined as (i.e., by measurement or calculation) of the any device that is capable of providing a absorbed dose or dose rate resulting from the interaction of ionizing radiation with matter reading R that is a measure of the absorbed • Other radiologically relevant quantities are dose Dg deposited in its sensitive volume V exposure, kerma, fluence, dose equivalent, energy by ionizing radiation imparted, etc. can be determined • If the dose is not homogeneous • Measuring one quantity (usually the absorbed dose) another one can be derived through throughout the sensitive calculations based on the defined relationships volume, then R is a measure of mean value Dg Dosimeter Simple dosimeter model • Ordinarily one is not interested in measuring • A dosimeter can generally be considered as the absorbed dose in a dosimeter’s sensitive consisting of a sensitive volume V filled with a volume itself, but rather as a means of medium g, surrounded by a wall (or envelope, determining the dose (or a related quantity) for container, etc.) of another medium w having a another medium in which direct measurements thickness t 0 are not feasible • A simple dosimeter can be
    [Show full text]
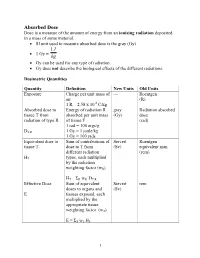
  • Absorbed Dose Dose Is a Measure of the Amount of Energy from an Ionizing Radiation Deposited in a Mass of Some Material
    Absorbed Dose Dose is a measure of the amount of energy from an ionizing radiation deposited in a mass of some material. • SI unit used to measure absorbed dose is the gray (Gy). 1J • 1 Gy = kg • Gy can be used for any type of radiation. • Gy does not describe the biological effects of the different radiations. Dosimetric Quantities Quantity Definition New Units Old Units Exposure Charge per unit mass of --- Roentgen air (R) 1 R = 2.58 x 10-4 C/kg Absorbed dose to Energy of radiation R gray Radiation absorbed tissue T from absorbed per unit mass (Gy) dose radiation of type R of tissue T (rad) 1 rad = 100 ergs/g DT,R 1 Gy = 1 joule/kg 1 Gy = 100 rads Equivalent dose to Sum of contributions of Sievert Roentgen tissue T dose to T from (Sv) equivalent man different radiation (rem) HT types, each multiplied by the radiation weighting factor (wR) HT = ΣR wR DT,R Effective Dose Sum of equivalent Sievert rem doses to organs and (Sv) E tissues exposed, each multiplied by the appropriate tissue weighting factor (wT) E = ΣT wT HT 1 Radiological Protection For practical purposes of assessing and regulating the hazards of ionizing radiation to workers and the general population, weighting factors (previously called quality factors, Q) are used. A radiation weighting factor is an estimate of the effectiveness per unit dose of the given radiation relative a to low-LET standard. Weighting factors are dimensionless multiplicative factors used to convert physical dose (Gy) to equivalent dose (Sv) ; i.e., to place biological effects from exposure to different types of radiation on a common scale.
    [Show full text]
  • Radiation: Units of Measure and Health Effects Gerald Gels Health Physicist Veridian Corporation Units of Measure
    Radiation: Units of Measure and Health Effects Gerald Gels Health Physicist Veridian Corporation Units of Measure • Traditional Unit 1 curie (Ci) = 3.7 x 1010 dps = 2.2 x 1012 dpm • Subunits 1 microcurie (µCi) = 1 x 10-6 Ci 1 picocurie (pCi) = 1 x 10-12 Ci • International System (SI) 1 becquerel (Bq) = 1 dps Ionization Density alpha m = 4; Z = +2 beta m = .0005; Z = -1 gamma m = 0; Z = 0 m = atomic mass units (amu) Z = electric charge units = ionizations roentgen (R): An amount of x- or gamma radiation that causes 1 esu (electrostatic unit) of charges due to ionization in 1 cc of air. Absorbed Dose The rad (r) [or Gray (Gy)] G. L. Gels The Roentgen (R) describes the radiation field (the agent); but, The rad (r) describes the effect in a medium. 1 rad = 100 ergs/gm 100 ergs of energy released per gram of medium a. applies to any medium (including air) b. applies to any type of radiation (not just photons) The Gray (Gy) = 100 rad (r) The rad is a medium-dependent quantity, and is very useful as an estimate of the effect of radiation in, say, tissue. However, it does not take into account the relative biological effects of different types of radiation. 1 rad = 0.87 R For air 1 rad = 0.98 R For soft tissue Dose Equivalent [rem or Seivert (Sv)] * Gamma rays have a much different biological effect than alpha particles * The Dose Equivalent modifies the absorbed dose (rad) by the relative biological effectiveness (or, Quality Factor, QF) of the radiation Radiation QF -rays X-rays } above .03 MeV 1 less than .03 MeV 1.7 Neutrons (thermal) 2 Neutrons (fast) Protons } 10 Alpha particles Heavy charged particles } 20 rem = rad x QF G.
    [Show full text]
  • Gate Frame Question
    UNIT THREE BIOLOGICAL EFFECTS AND INTERNAL HAZARDS OF RADIATION EXPOSURE Unit Two reviewed the mechanism by which ionizing radiation may cause biological damage. That mechanism can be summarized by saying that ions created by radiation, as well as new compounds formed by the pairing up of the ions, disrupt cell organization and function. For radiological emergency responders, the potential biological effects of radiation exposure are important considerations. You have studied biological effects and internal hazards of radiation in other courses. This unit will incorporate a review of some important basic concepts and introduce a few new terms and details that will better prepare you for radiological emergency response operations. GATE FRAME You have responded to an accident involving a truck containing radionuclides destined for a research facility. QUESTION The Incident Commander tells you that a package found on the ground indicates that it contains 0.2 Ci of iodine-131 (I-131). I-131 is a beta emitter, with a radioactive half-life of 8 days. What potential biological effects are associated with radia- tion exposure to this type of material, and what factors determine the extent of potential biological damage by this material? (Use another sheet if needed.) 3-1 Unit Three Biological Effects and Internal Hazards of Radiation Exposure ANSWER The radiation health effects from beta-emitting radionuclides such as I-131 may be early (acute) or late (chronic). Early affects, which occur within two or three months after exposure, include skin damage (such as “beta burns”), loss Your answer should of appetite, nausea, fatigue, and diarrhea. Late effects, include the adjacent which can occur years after exposure, include cancer, information.
    [Show full text]
  • Radiation Safety
    RADIATION SAFETY FOR LABORATORY WORKERS RADIATION SAFETY PROGRAM DEPARTMENT OF ENVIRONMENTAL HEALTH, SAFETY AND RISK MANAGEMENT UNIVERSITY OF WISCONSIN-MILWAUKEE P.O. BOX 413 LAPHAM HALL, ROOM B10 MILWAUKEE, WISCONSIN 53201 (414) 229-4275 SEPTEMBER 1997 (REVISED FROM JANUARY 1995 EDITION) CHAPTER 1 RADIATION AND RADIOISOTOPES Radiation is simply the movement of energy through space or another media in the form of waves, particles, or rays. Radioactivity is the name given to the natural breakup of atoms which spontaneously emit particles or gamma/X energies following unstable atomic configuration of the nucleus, electron capture or spontaneous fission. ATOMIC STRUCTURE The universe is filled with matter composed of elements and compounds. Elements are substances that cannot be broken down into simpler substances by ordinary chemical processes (e.g., oxygen) while compounds consist of two or more elements chemically linked in definite proportions. Water, a compound, consists of two hydrogen and one oxygen atom as shown in its formula H2O. While it may appear that the atom is the basic building block of nature, the atom itself is composed of three smaller, more fundamental particles called protons, neutrons and electrons. The proton (p) is a positively charged particle with a magnitude one charge unit (1.602 x 10-19 coulomb) and a mass of approximately one atomic mass unit (1 amu = 1.66x10-24 gram). The electron (e-) is a negatively charged particle and has the same magnitude charge (1.602 x 10-19 coulomb) as the proton. The electron has a negligible mass of only 1/1840 atomic mass units. The neutron, (n) is an uncharged particle that is often thought of as a combination of a proton and an electron because it is electrically neutral and has a mass of approximately one atomic mass unit.
    [Show full text]
  • Quick Reference Guide: Radiation Risk Information for Responders Following a Nuclear Detonation
    December 2016 Quick Reference Guide: Radiation Risk Information for Responders Following a Nuclear Detonation Quick Reference Guide This document supports the “Planning Guidance for Response to a Nuclear Detonation” and was designed to provide responders with specific guidance and recommendations about the radiation risk associated with responding to an improvised nuclear device (IND) event, in order for them to protect themselves from the IND effects. It is intended to be part of preparation training with the “Health and Safety Planning Guide For Planners and Supervisors For Protecting First Responders Following A Nuclear Detonation”. This provides basic information responders will need for the first 24 -72 hours after an extreme event - - a nuclear detonation. These guidelines are not designed to apply to other, less extreme, radiological events. Specific information/training should be sought for those. Some of this guidance will be counterintuitive to those trained in emergency response; however, it is critical that responders remain as safe and healthy as possible, not only for their own safety, but also to remain available for the ongoing mission of saving lives. Responders involved in an IND event need to be prepared to see numerous victims with serious traumatic injuries and illness including: severe burns, blindness, deafness, amputations, radiation sickness, etc. What would a nuclear detonation be like and what can you expect? • The Nuclear Flash would come in the form of an intense burst of light and extreme heat potentially creating a firestorm. Injuries: flash burns, flame burns, flash blindness, and retina burns. • Prompt Radiation would be delivered, resulting in high radiation doses close to the detonation.
    [Show full text]
  • Biological Effects from Acute Exposures
    Biological Effects from Acute Exposures Professional Personnel July 2002 Fact Sheet 320-064 Division of Environmental Health Office of Radiation Protection ASSESSMENT AND TREATMENT OF RADIATION INJURY Emergency personnel may be required to perform duties in a nuclear radiation environment. An accident may already have occurred, resulting in the spread of contamination, or there may be the potential for exposure. Operational considerations may require that emergency response be conducted in that environment for a protracted period of time. It is critical that all personnel be protected to reduce or avoid short-term, or acute, exposures to radiation. The Office of Radiation Protection serves as a resource for consultation on matters related to the effects of radiation. Our activities involve working with emergency and medical personnel to coordinate resources necessary to determine or assess the effects of radiation exposure. BIOLOGICAL EFFECTS The average person in the U.S. is exposed to background radiation levels that would result in an annual dose of approximately 360 mrem. Higher and more short-term doses, although unlikely, are termed acute exposures. Whole-body doses of radiation (of the type in X-ray or gamma radiation) in significant doses of 35 rad can cause nausea, weakness and appetite loss within a few hours following an acute exposure. These symptoms will disappear within a few hours of the exposure. After doses of 50 rad or above from acute radiation exposures, many immune competent cells are used up defending the body from infection, and others are prevented from performing their duty. Virtually no new replacement cells are produced because of the extensive damage to stem cells in bone marrow.
    [Show full text]
  • Table of Contents
    ORAU Team Document Number: ORAUT-TKBS-0006-6 NIOSH Dose Reconstruction Project Effective Date: 10/05/2006 Revision No.: 01 PC-1 Technical Basis Document for the Hanford Site – Controlled Copy No.: ______ Occupational External Dosimetry Page 1 of 80 Subject Expert: Jack Fix Supersedes: Document Owner Approval: Signature on File Date: 01/09/2004 Edward D. Scalsky, TBD Team Leader Revision No.: 00 Approval: Signature on File Date: 01/09/2004 Judson L. Kenoyer, Task 3 Manager Concurrence: Signature on File Date: 01/09/2004 Richard E. Toohey, Project Director Approval: Signature on File Date: 01/09/2004 James W. Neton, OCAS Health Science Administrator TABLE OF CONTENTS Section Page Record of Issue/Revisions ................................................................................................................... 5 Acronyms and Abbreviations ............................................................................................................... 6 6.1 Introduction ................................................................................................................................. 8 6.1.1 Purpose ............................................................................................................................ 9 6.1.2 Scope ............................................................................................................................... 9 6.2 External Dosimetry ...................................................................................................................... 9 6.3 Basis of
    [Show full text]