Chapter 3: Radiation Dosimeters
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Utilization of MOSFET Dosimeters for Clinical Measurements in Radiology
The Utilization of MOSFET Dosimeters for Clinical Measurements in Radiology David Hintenlang, Ph.D., DABR, FACMP Medical Physics Program Director J. Crayton Pruitt Family Department of Biomedical Engineering J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program Conflict of interest statement: The presenter holds no financial interest in, and has no affiliation or research support from any manufacturer or distributor of MOSFET Dosimetry systems. J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program The MOSFET Dosimeter • Metal oxide silicon field effect transistor • Uniquely packaged to serve as a radiation detector – developed as early as 1974 • Applications – Radiation Therapy Dose Verification – Cosmic dose monitoring on satellites – Radiology • ~ 1998 - present J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program Attractive features • Purely electronic dosimeter • Provides immediate dose feedback • Integrates over short periods of time • Small size and portability • Simultaneous measurements (up to 20) J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program Demonstrated radiology applications – Patient dose monitoring/evaluation • Radiography • Fluoroscopic and interventional procedures • CT • Mammography J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program Principles of operation • Ionizing radiation results in the creation of electron-hole pairs • Holes migrate and build up -

Absorbed Dose in Radioactive Media Outline Introduction Radiation Equilibrium Charged-Particle Equilibrium Limiting Cases
Outline • General dose calculation considerations, Absorbed Dose in Radioactive absorbed fraction Media • Radioactive disintegration processes and associated dose deposition – Alpha disintegration Chapter 5 – Beta disintegration – Electron-capture transitions F.A. Attix, Introduction to Radiological – Internal conversion Physics and Radiation Dosimetry • Summary Introduction Radiation equilibrium • We are interested in calculating the absorbed dose in a. The atomic composition radioactive media, applicable to cases of of the medium is – Dose within a radioactive organ homogeneous – Dose in one organ due to radioactive source in another b. The density of the organ medium is • If conditions of CPE or RE are satisfied, dose homogeneous c. The radioactive source calculation is straightforward is uniformly distributed • Intermediate situation is more difficult but can be d. No external electric or handled at least in approximations magnetic fields are present Charged-particle equilibrium Limiting cases • Emitted radiation typically includes both • Each charged particle of a given type and photons (longer range) and charged energy leaving the volume is replaced by an particles (shorter range) identical particle of the same energy entering • Assume the conditions for RE are satisfied the volume • Consider two • Existence of RE is sufficient condition for CPE limited cases based • Even if RE does not exist CPE may still exist on the size of the (for a very large or a very small volume) radioactive object 1 Limiting cases: small object Limiting -

Experiment "Gamma Dosimetry and Dose Rate Determination" Instruction for Experiment "Gamma Dosimetry and Dose Rate Determination"
TECHNICAL UNIVERSITY DRESDEN Institute of Power Engineering Training Reactor Reactor Training Course Experiment "Gamma Dosimetry and Dose Rate Determination" Instruction for Experiment "Gamma Dosimetry and Dose Rate Determination" Content: 1 .... Motivation 2..... Theoretical Background 2.1... Properties of Ionising Radiation and Interactions of Gamma Radiation 2.2. Detection of Ionising Radiation 2.3. Quantities and Units of Dosimetry 3..... Procedure of the Experiment 3.1. Commissioning and Calibration of the Dosimeter Thermo FH40G 3.2. Commissioning and Calibration of the Dosimeter Berthold LB 133-1 3.3. Commissioning and Calibration of the Dosimeter STEP RGD 27091 3.4. Setup of the Experiment 3.4.1. Measurement of Dose Rate in Various Distances from the Radiation Source 3.4.2. Measurement of Dose Rate behind Radiation Shielding 3.5. Measurement of Dose Rate at the open Reactor Channel 4..... Evaluation of Measuring Results Figures: Fig. 1: Composition of the attenuation coefficient µ of γ-radiation in lead Fig. 2: Design of an ionisation chamber Fig. 3: Classification and legal limit values of radiation protection areas Fig. 4: Setup of the experiment (issued: January 2019) - 1 - 1. Motivation The experiment aims on familiarising with the methods of calibrating different detectors for determination of the dose and the dose rate. Furthermore, the dose rate and the activity in the vicinity of an enclosed source of ionising radiation (Cs-137) will be determined taking into account the background radiation and the measurement accuracy. Additionally, the experiment focuses on the determination of the dose rate of a shielded source as well as on the calculation of the required thickness of the shielding protection layer for meeting the permissible maximum dose rate. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

RAD 520-3 the Physics of Medical Dosimetry
RAD 520 The Physics of Medical Dosimetry I Fall Semester Syllabus COURSE DEFINITION: RAD 520-3 The Physics of Medical Dosimetry I- This course covers the following topics: Radiologic Physics, production of x-rays, radiation treatment and simulation machines, interactions of ionizing radiation, radiation measurements, dose calculations, computerized treatment planning, dose calculation algorithms, electron beam characteristics, and brachytherapy physics and procedures. This course is twenty weeks in length. Prerequisite: Admission to the Medical Dosimetry Program. COURSE OBJECTIVES: 1. Demonstrate an understanding of radiation physics for photons and electrons. 2. Demonstrate an understanding of the different types of radiation production. 3. Demonstrate an understanding of radiation dose calculations and algorithms. 4. Understand brachytherapy procedures and calculate radiation attenuation and decay. 5. Demonstrate an understanding of the different types of radiation detectors. 6. Demonstrate an understanding of general treatment planning. COURSE OUTLINE: Topics 1. Radiation physics 2. Radiation generators 3. External beam calculations 4. Brachytherapy calculations 5. Treatment planning 6. Electron beam physics COURSE REQUIREMENTS: Purchase all texts, attend all lectures, and complete required examinations, quizzes, and homeworks. Purchase a T130XA scientific calculator. PREREQUISITES: Admittance to the Medical Dosimetry Program. TEXTBOOKS: Required: 1. Khan, F. M. (2014). The physics of radiation therapy (5th ed.). Philadelphia: Wolters Kluwer 2. Khan, F.M. (2016). Treatment planning in radiation oncology (4th ed.). Philadelphia: Wolters Kluwer 3. Washington, C. M., & Leaver, D. T. (2015). Principles and practices of radiation therapy (4th Ed). St. Louis: Mosby. Optional: (Students typically use clinical sites’ copy) 1. Bentel, G. C. (1992). Radiation therapy planning (2nd ed.). New York: McGraw-Hill. -

Development of Chemical Dosimeters Development Of
SUDANSUDAN ACADEMYAGADEMY OFOF SCIENCES(SAS)SGIENGES(SAS) ATOMICATOMIC ENERGYEhTERGYRESEARCHESRESEARCHES COORDINATIONCOORDII\rATI ON COUNCILCOUNCIL - Development of Chemical Dosimeters A dissertation Submitted in a partial Fulfillment of the Requirement forfbr Diploma Degree in Nuclear Science (Chemistry) By FareedFadl Alla MersaniMergani SupervisorDr K.S.Adam MurchMarch 2006 J - - - CONTENTS Subject Page -I - DedicationDedication........ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... I Acknowledgement ... '" ... ... ... ... ... ... '" ... ... ... ... '" ... '" ....... .. 11II Abstract ... ... ... '" ... ... ... '" ... ... ... ... -..... ... ... ... ... ... ..... III -I Ch-lch-1 DosimetryDosimefry - 1-1t-l IntroductionLntroduction . 1I - 1-2t-2 Principle of Dosimetry '" '" . 2 1-3l-3 DosimetryDosimefiySystems . 3J 1-3-1l-3-l primary standard dosimeters '" . 4 - 1-3-2l-3-Z Reference standard dosimeters ... .. " . 4 1-3-3L-3-3 Transfer standard dosimeters ... ... '" . 4 1-3-4t-3-4 Routine dosimeters . 5 1-4I-4 Measurement of absorbed dose . 6 1-5l-5 Calibration of DosimetryDosimetrvsystemsvstem '" . 6 1-6l-6 Transit dose effects . 8 Ch-2ch-2 Requirements of chemical dosimeters 2-12-l Introduction ... ... ... .............................................. 111l 2-2 Developing of chemical dosimeters ... ... .. ....... ... .. ..... 12t2 2-3 Classification of Dosimetry methods.methods .......................... 14l4 2-4 RequirementsRequiremsnts of ideal chemical dosimeters ,. ... 15 2-5 Types of chemical system . -

The International Commission on Radiological Protection: Historical Overview
Topical report The International Commission on Radiological Protection: Historical overview The ICRP is revising its basic recommendations by Dr H. Smith Within a few weeks of Roentgen's discovery of gamma rays; 1.5 roentgen per working week for radia- X-rays, the potential of the technique for diagnosing tion, affecting only superficial tissues; and 0.03 roentgen fractures became apparent, but acute adverse effects per working week for neutrons. (such as hair loss, erythema, and dermatitis) made hospital personnel aware of the need to avoid over- Recommendations in the 1950s exposure. Similar undesirable acute effects were By then, it was accepted that the roentgen was reported shortly after the discovery of radium and its inappropriate as a measure of exposure. In 1953, the medical applications. Notwithstanding these observa- ICRU recommended that limits of exposure should be tions, protection of staff exposed to X-rays and gamma based on consideration of the energy absorbed in tissues rays from radium was poorly co-ordinated. and introduced the rad (radiation absorbed dose) as a The British X-ray and Radium Protection Committee unit of absorbed dose (that is, energy imparted by radia- and the American Roentgen Ray Society proposed tion to a unit mass of tissue). In 1954, the ICRP general radiation protection recommendations in the introduced the rem (roentgen equivalent man) as a unit early 1920s. In 1925, at the First International Congress of absorbed dose weighted for the way different types of of Radiology, the need for quantifying exposure was radiation distribute energy in tissue (called the dose recognized. As a result, in 1928 the roentgen was equivalent in 1966). -

MIRD Pamphlet No. 22 - Radiobiology and Dosimetry of Alpha- Particle Emitters for Targeted Radionuclide Therapy
Alpha-Particle Emitter Dosimetry MIRD Pamphlet No. 22 - Radiobiology and Dosimetry of Alpha- Particle Emitters for Targeted Radionuclide Therapy George Sgouros1, John C. Roeske2, Michael R. McDevitt3, Stig Palm4, Barry J. Allen5, Darrell R. Fisher6, A. Bertrand Brill7, Hong Song1, Roger W. Howell8, Gamal Akabani9 1Radiology and Radiological Science, Johns Hopkins University, Baltimore MD 2Radiation Oncology, Loyola University Medical Center, Maywood IL 3Medicine and Radiology, Memorial Sloan-Kettering Cancer Center, New York NY 4International Atomic Energy Agency, Vienna, Austria 5Centre for Experimental Radiation Oncology, St. George Cancer Centre, Kagarah, Australia 6Radioisotopes Program, Pacific Northwest National Laboratory, Richland WA 7Department of Radiology, Vanderbilt University, Nashville TN 8Division of Radiation Research, Department of Radiology, New Jersey Medical School, University of Medicine and Dentistry of New Jersey, Newark NJ 9Food and Drug Administration, Rockville MD In collaboration with the SNM MIRD Committee: Wesley E. Bolch, A Bertrand Brill, Darrell R. Fisher, Roger W. Howell, Ruby F. Meredith, George Sgouros (Chairman), Barry W. Wessels, Pat B. Zanzonico Correspondence and reprint requests to: George Sgouros, Ph.D. Department of Radiology and Radiological Science CRB II 4M61 / 1550 Orleans St Johns Hopkins University, School of Medicine Baltimore MD 21231 410 614 0116 (voice); 413 487-3753 (FAX) [email protected] (e-mail) - 1 - Alpha-Particle Emitter Dosimetry INDEX A B S T R A C T......................................................................................................................... -

Chapter 2 Radiation Safety Manual Revision 1 Principles of Radiation Safety 6/1/2018
The University of Georgia Chapter 2 Radiation Safety Manual Revision 1 Principles of Radiation Safety 6/1/2018 CHAPTER 2 PRINCIPLES OF RADIATION SAFETY 1.0 UNITS OF RADIATION DOSE 1.1 Historical Units In 1896, x-rays were discovered by Wilhelm Roentgen. The Roentgen is unit of measurement for the exposure of x-rays and gamma rays. It is defined as the electric charge freed by such radiation in a specified volume of air divided by the mass of that air. Radioactivity was discovered by Henri Becquerel. Radioactivity refers to the amount of radiation released when an element spontaneously emits energy as a result of the decay of its unstable atoms. The Becquerel is a unit used to measure radioactivity, and stands for 1 disintegration per second. The Curie is a unit of radioactivity equal to 3.7 X 1010 disintegrations per second and was first used, but being such a large unit was replaced by the Becquerel. The Curie is named for Pierre Curie, Marie Curie’s husband and co- discoverer of radium. After his accidental death, she continued their work. For some time, no one realized that radiation could cause harmful effects. It was recognized very soon that x-rays could be used in medical diagnosis, and early radiologists received large doses of radiation. Many of these radiologists later suffered severe injuries due to overexposure (radiation effects may appear years after exposure). The first unit of dose was the erythema dose. This was the amount of x-radiation which would barely cause reddening of the skin. It was not a very satisfactory unit of dose, but indicates the early recognition by some scientists that radiation exposure can be harmful and should be limited. -
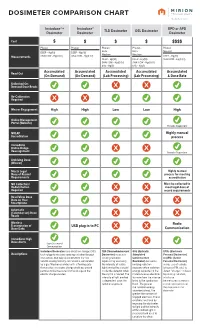
Dosimeter Comparison Chart
DOSIMETER COMPARISON CHART Instadose®+ Instadose® EPD or APD TLD Dosimeter OSL Dosimeter Dosimeter Dosimeter Dosimeter Cost $ $ $ $$$$ Photon Photon Photon Photon Photon Beta Beta Neutron DEEP - Hp(10) DEEP - Hp(10) Neutron Neutron Measurements SHALLOW - Hp(0.07) SHALLOW - Hp(0.07) DEEP - Hp(10) DEEP - Hp(10) DEEP - Hp(10) SHALLOW - Hp(0.07) SHALLOW - Hp(0.07) SHALLOW - Hp(0.07) EYE - Hp(3) EYE - Hp(3) Read Out Accumulated Accumulated Accumulated Accumulated Accumulated (On-Demand) (On-Demand) (Lab Processing) (Lab Processing) & Dose Rate Unlimited On- Demand Dose Reads Re-Calibration Required Wearer Engagement High High Low Low High Online Management Portal (Website) Provider Dependent NVLAP Highly manual Accreditation process Immediate Online Badge Reassignment Provider Dependent Archiving Dose (Wearer) Meets Legal Highly manual Dose of Record process for meeting Requirements accreditation NO Collection/ Must be collected to Redistribution meet legal dose of Required record requirements Read/View Dose Data on Your Smartphone Automatic (Calendar-set) Dose Reads Wireless Radio Transmission of USB plug-in to PC Dose Data Communication Immediate High Dose Alerts Upon Successful Communication Instadose Dosimeters use direct ion storage (DIS) TLD (Thermoluminescent OSL (Optically EPDs (Electronic Descriptions technology to measure ionizing radiation through Dosimeter) measures Stimulated Personal Dosimeter) interactions that take place between the non- ionizing radiation Luminescence or APDs (Active volatile analog memory cell, which is surrounded exposure by assessing Dosimeter) measures Personal Dosimeter) by a gas filled ion chamber with a floating gate the intensity of visible ionizing radiation makes use of a diode that creates an electric charge enabling ionized light emitted by a crystal exposure when radiation (silicon or PIN, etc.) to particles to be measured by the change in the inside the detector when energy deposited in the detect “charges” induced electric charge created. -

Site-Specific Calibration of the Hanford Personnel Neutron Dosimeter
Gw^HI0n--7 PNL-SA-24010 SITE-SPECIFIC CALIBRATION OF THE HANFORD PERSONNEL NEUTRON DOSIMETER BEC 2 7 mm A. W. Endres Q o 7- L. W. Brackenbush ° f W. V. Baumgartner B. A. Rathbone October 1994 Presented at the Fourth Conference on Radiation Protection and Dosimetry October 23-27, 1994 Orlando, Florida Prepared for the U.S. Department of Energy under Contract DE-AC06-76RLO 1830 Pacific Northwest Laboratory Richland, Washington 99352 DISCLAIMER This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsi• bility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Refer• ence herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recom• mendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. MUM1TED 4STR1BUTION Or TH« DU^- to u G£ DISCLAIMER Portions of this document may be illegible in electronic image products. Images are produced from the best available original document. SITE-SPECIFIC CALIBRATION OF THE HANFORD PERSONNEL NEUTRON DOSIMETER A. W. Endres, L. W. Brackenbush, W. V. Baumgartner, and B. A. Rathbone Pacific Northwest Laboratory, Richland, Washington 99352 INTRODUCTION A new personnel dosimetry system, employing a standard Hanford thermo• luminescent dosimeter (TLD) and a combination dosimeter with both CR-39 nuclear track and TLD-albedo elements, is being implemented at Hanford. -

Colorado Metric Conversion Manual
COLORADO OT . DEPARTMENT OF TRANSPORTATION METRIC CONVERSION MANUAL January 1994 This manual or any part thereof must not be reproduced in any form without the following disclaimer. The information presented in this publication haS been prepared in accordance with recognized engineering principles and is for general information only. While it is believed to be accurate, this information should not be used or relied upon for any specific application without competent professional examination and verification of its accuracy, suitability, and applicability by a competent licensed engineer or other licensed professional. Publication of the material contained herein is not intended as a representation or warranty on the part of the Colorado Department of Transportation (CDOT) , that this information is suitable for any general or particular use or of freedom from infringement of any patent or patents. Anyone making use of this information assumes all liability arising from such use. Caution must be exercised when relying upon the specifications and codes developed by other bodies and incorporated herein, since such material may be modified or amended from time to time subsequent to the printing of this edition. COOT bears no responsibility for such material other than to incorporate it at the time of the initial publication of this edition, subject to the general comments set forth in the preceding paragraph. Table of Contents Preface ................................................... v Introduction . vii Chapter 1: Metric Units, Terms, Symbols, and Conversion Factors . ... 1-1 Basic Metric . 1-1 Length, Area, Volume and Temperature . 1-7 Civil and Structural Engineering . 1-10 Metric Project Definition ....................... .. 1-12 Chapter 2: Right-Of-Way ...................................