DOCSLIB.ORG

11. Dosimetry Fundamentals

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
11. Dosimetry Fundamentals Outline • Introduction Dosimetry Fundamentals • Dosimeter model • Interpretation of dosimeter measurements Chapter 11 – Photons and neutrons – Charged particles • General characteristics of dosimeters F.A. Attix, Introduction to Radiological Physics and Radiation Dosimetry • Summary Introduction Dosimeter • Radiation dosimetry deals with the determination • A dosimeter can be generally defined as (i.e., by measurement or calculation) of the any device that is capable of providing a absorbed dose or dose rate resulting from the interaction of ionizing radiation with matter reading R that is a measure of the absorbed • Other radiologically relevant quantities are dose Dg deposited in its sensitive volume V exposure, kerma, fluence, dose equivalent, energy by ionizing radiation imparted, etc. can be determined • If the dose is not homogeneous • Measuring one quantity (usually the absorbed dose) another one can be derived through throughout the sensitive calculations based on the defined relationships volume, then R is a measure of mean value Dg Dosimeter Simple dosimeter model • Ordinarily one is not interested in measuring • A dosimeter can generally be considered as the absorbed dose in a dosimeter’s sensitive consisting of a sensitive volume V filled with a volume itself, but rather as a means of medium g, surrounded by a wall (or envelope, determining the dose (or a related quantity) for container, etc.) of another medium w having a another medium in which direct measurements thickness t 0 are not feasible • A simple dosimeter can be treated in terms of cavity theory, the sensitive • Interpretation of a dosimeter reading is the volume being identified as the central problem in dosimetry, usually “cavity”, which may contain a exceeding in difficulty the actual measurement gaseous, liquid, or solid medium g 1 Interpretation of dosimeter Simple dosimeter model measurements: photons and neutrons • The dosimeter wall can serve a number of functions simultaneously: • Under CPE condition – being a source of secondary charged particles that contribute CPE DK Y/ to the dose in V, and provide CPE or TCPE in some cases c en – shielding V from charged particles that originate outside the • Consider a dosimeter with a wall of medium w, thick enough wall to exclude all charged particles generated elsewhere, and at – protecting V from “hostile” influences such as mechanical least as thick as the maximum range of secondary charged damage, dirt, humidity, light, electrostatic or RF fields, etc., particles generated in it by the photon or neutron field that may alter the reading • If the wall is uniformly irradiated, CPE exists in the wall – serving as a container for g that is a gas, liquid, or powder near the cavity, therefore knowing D can calculate energy – containing radiation filters to modify the energy dependency w fluence Y of the primary field of the dosimeter Interpretation of dosimeter Interpretation of dosimeter measurements: photons and neutrons measurements: photons and neutrons • The dosimeter reading provides us with a measure • For neutrons the CPE condition results in of the dose Dg in the dosimeter’s sensitive volume CPE DKF F n • If the latter is small enough to satisfy the B-G conditions, we can find Dw from Dg Fn is kerma-factor, F is neutron fluence • The dose Dx in any other medium x replacing the • Therefore the dose D in the medium of interest x dosimeter and given an identical irradiation under x CPE conditions can be obtained from CPE F n x CPE DDxw for neutrons en / x Fn Dx Dw for photons w en / w Interpretation of dosimeter Interpretation of dosimeter measurements: photons and neutrons measurements: photons and neutrons • For higher-energy radiation (h 1 MeV or Tn • The exposure X (C/kg) for photons can in turn be 10 MeV), CPE fails but TCPE takes its place in derived from the absorbed dose Dair (for x = air) dosimeters with walls of sufficient thickness through this relation: • For photons TCPE condition provides relationship CPE e Dair TCPE XDair D Kcc1/ x K Y en W air 33.97 • For neutrons TCPE • This relationship can be extended for higher D K1 x K F F n energies where TCPE exists, dividing Dair by • Relating Dw to Y or F then requires evaluation of = D/Kc for each case 2 Interpretation of dosimeter measurements: photons and neutrons Media matching • The value of is generally not much greater than • If media of interest (x), wall (w), and gas (g) are the unity for radiation energies up to a few tens of MeV, same, the measurement directly provides the dose of and it is not strongly dependent on atomic number interest. If these media are matched: – Influence of cavity theory is minimized • Thus for media w and x not differing very greatly in – No need to know the radiation energy spectrum Z, the equations for D are still approximately valid x • Matching parameters: • If the dosimeter has too large a sensitive volume for – Atomic compositions the application of B-G theory, Burlin theory can be used to calculate the equilibrium dose D from – The density state (gaseous vs. condensed), which w influences the collision-stopping-power ratios for electrons – requires sensitive-volume size d parameter by the polarization effect Media matching in photon Media matching dosimeters (w=g) • w=g: if the wall and sensitive-volume media of the • The Burlin cavity relation dosimeter are identical with respect to composition g Dg g en d mw S (1 d ) and density, then Dw = Dg for all homogeneous Dw irradiations w • If w and g are matched, the doses Dw= Dg and • w=g=x: the dosimeter would be truly representative g g en of that medium with respect to radiation interactions, mwS 1 and Dx = Dw = Dg w • Unfortunately, dosimeters are only available in a • This relationship is hard to satisfy, especially for w finite variety, therefore have to rely on cavity theory and g of different atomic compositions D g Media matching in photon Matching the dosimeter to the dosimeters (w=g) medium of interest when w≠g • A more flexible and practical relationship • If the wall medium wg, matching to medium x g g en depends on the dosimeter volume size mwSn w • If the sensitive volume is small (d = 1 in Burlin’s cavity • The Burling relation then becomes independent of d theory), then the wall should be matched to medium x, to minimize the need for spectral information since Dg / Dw n • It is relevant, for example, if photons interact only • Dose in x can be obtained from by the Compton effect in g and w: en/ ~the mass w collision scattering power of the secondary electrons DDD ggw S g en ~ to the number of electrons per gram, NAZ/A; mw DDDx w x x n (Z/A) /(Z/A) g w B-G 3 Matching the dosimeter to the Correcting for attenuation of medium of interest when w≠g radiation • The problem arises from the difference in attenuation by • If the sensitive volume is large (d = 0 in Burlin’s media x (for example, water), w (thickness t) and g (radius r) cavity theory), the wall influence on the dose in the • The photon energy fluence reaching the center of a dosimeter medium g is entirely lost Y Y 1 en t en r dos 0 w g • Medium x should be matched to g and dose in x can be w g obtained from • On the other hand energy fluence reaching the water sphere g w g replacing the dosimeter DD ggDw en en en en Ywat Y0 1 wat (t r) wat DDDx w x w x x • The dosimeter reading should be multiplied by Ywat/Ydos to • For a general case of intermediate size cavity (0<d<1) correct for the difference of attenuation in determining the full Burlin equation can be used to obtain Dw from Dg dose to water at the dosimeter midpoint Importance of dosimeter wall Interpretation of dosimeter thickness measurements: charged particles • Dosimeter wall thickness requirement depends on the goal • The absorbed dose at a point in a medium x is the of a measurement: to obtain a quantity that depends on product of the charged-particle fluence (not the a) the characteristics of the local photon or neutron field, energy fluence) and the mass collision stopping the dosimeter should have a wall at least as thick as the power, assuming that CPE exists for -rays maximum range of the charged particles present, to provide CPE or TCPE Tmax dT Dx FT dT b) the characteristics of the local secondary charged-particle 0 dx field then the dosimeter wall and sensitive volume should c,x both be thin enough not to interfere with the passage of • The integration is over all energies in the primary incident charged particles (i.e., non--ray) charged-particle spectrum F(T) Interpretation of dosimeter Interpretation of dosimeter measurements: charged particles measurements: charged particles • Charged particle dosimeter needs a sensitive volume Approximate CSDA ranges of electrons and protons in water small (or thin) enough to satisfy the B-G conditions (nonperturbation of the charged-particle field), and all dose to be deposited only by crossers • The dosimeter wall should be thick enough to serve any essential functions (e.g., containment) • Thin flat pillbox- or coin-shaped dosimeters, • As a rule of thumb: neither the wall thickness nor that of the sensitive volume should exceed ~1% of oriented perpendicularly to the particle-beam the range of the incident charged particles direction, are used to satisfy these requirements • Ranges in other low-Z media are comparable 4 Interpretation of dosimeter Interpretation of dosimeter measurements: charged particles measurements: charged particles • One of the functions
Load more

Recommended publications
  • The Utilization of MOSFET Dosimeters for Clinical Measurements in Radiology
    The Utilization of MOSFET Dosimeters for Clinical Measurements in Radiology David Hintenlang, Ph.D., DABR, FACMP Medical Physics Program Director J. Crayton Pruitt Family Department of Biomedical Engineering J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program Conflict of interest statement: The presenter holds no financial interest in, and has no affiliation or research support from any manufacturer or distributor of MOSFET Dosimetry systems. J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program The MOSFET Dosimeter • Metal oxide silicon field effect transistor • Uniquely packaged to serve as a radiation detector – developed as early as 1974 • Applications – Radiation Therapy Dose Verification – Cosmic dose monitoring on satellites – Radiology • ~ 1998 - present J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program Attractive features • Purely electronic dosimeter • Provides immediate dose feedback • Integrates over short periods of time • Small size and portability • Simultaneous measurements (up to 20) J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program Demonstrated radiology applications – Patient dose monitoring/evaluation • Radiography • Fluoroscopic and interventional procedures • CT • Mammography J. Crayton Pruitt Family Department of Biomedical Engineering Medical Physics Program Principles of operation • Ionizing radiation results in the creation of electron-hole pairs • Holes migrate and build up
    [Show full text]
  • Absorbed Dose in Radioactive Media Outline Introduction Radiation Equilibrium Charged-Particle Equilibrium Limiting Cases
    Outline • General dose calculation considerations, Absorbed Dose in Radioactive absorbed fraction Media • Radioactive disintegration processes and associated dose deposition – Alpha disintegration Chapter 5 – Beta disintegration – Electron-capture transitions F.A. Attix, Introduction to Radiological – Internal conversion Physics and Radiation Dosimetry • Summary Introduction Radiation equilibrium • We are interested in calculating the absorbed dose in a. The atomic composition radioactive media, applicable to cases of of the medium is – Dose within a radioactive organ homogeneous – Dose in one organ due to radioactive source in another b. The density of the organ medium is • If conditions of CPE or RE are satisfied, dose homogeneous c. The radioactive source calculation is straightforward is uniformly distributed • Intermediate situation is more difficult but can be d. No external electric or handled at least in approximations magnetic fields are present Charged-particle equilibrium Limiting cases • Emitted radiation typically includes both • Each charged particle of a given type and photons (longer range) and charged energy leaving the volume is replaced by an particles (shorter range) identical particle of the same energy entering • Assume the conditions for RE are satisfied the volume • Consider two • Existence of RE is sufficient condition for CPE limited cases based • Even if RE does not exist CPE may still exist on the size of the (for a very large or a very small volume) radioactive object 1 Limiting cases: small object Limiting
    [Show full text]
  • Experiment "Gamma Dosimetry and Dose Rate Determination" Instruction for Experiment "Gamma Dosimetry and Dose Rate Determination"
    TECHNICAL UNIVERSITY DRESDEN Institute of Power Engineering Training Reactor Reactor Training Course Experiment "Gamma Dosimetry and Dose Rate Determination" Instruction for Experiment "Gamma Dosimetry and Dose Rate Determination" Content: 1 .... Motivation 2..... Theoretical Background 2.1... Properties of Ionising Radiation and Interactions of Gamma Radiation 2.2. Detection of Ionising Radiation 2.3. Quantities and Units of Dosimetry 3..... Procedure of the Experiment 3.1. Commissioning and Calibration of the Dosimeter Thermo FH40G 3.2. Commissioning and Calibration of the Dosimeter Berthold LB 133-1 3.3. Commissioning and Calibration of the Dosimeter STEP RGD 27091 3.4. Setup of the Experiment 3.4.1. Measurement of Dose Rate in Various Distances from the Radiation Source 3.4.2. Measurement of Dose Rate behind Radiation Shielding 3.5. Measurement of Dose Rate at the open Reactor Channel 4..... Evaluation of Measuring Results Figures: Fig. 1: Composition of the attenuation coefficient µ of γ-radiation in lead Fig. 2: Design of an ionisation chamber Fig. 3: Classification and legal limit values of radiation protection areas Fig. 4: Setup of the experiment (issued: January 2019) - 1 - 1. Motivation The experiment aims on familiarising with the methods of calibrating different detectors for determination of the dose and the dose rate. Furthermore, the dose rate and the activity in the vicinity of an enclosed source of ionising radiation (Cs-137) will be determined taking into account the background radiation and the measurement accuracy. Additionally, the experiment focuses on the determination of the dose rate of a shielded source as well as on the calculation of the required thickness of the shielding protection layer for meeting the permissible maximum dose rate.
    [Show full text]
  • Development of Chemical Dosimeters Development Of
    SUDANSUDAN ACADEMYAGADEMY OFOF SCIENCES(SAS)SGIENGES(SAS) ATOMICATOMIC ENERGYEhTERGYRESEARCHESRESEARCHES COORDINATIONCOORDII\rATI ON COUNCILCOUNCIL - Development of Chemical Dosimeters A dissertation Submitted in a partial Fulfillment of the Requirement forfbr Diploma Degree in Nuclear Science (Chemistry) By FareedFadl Alla MersaniMergani SupervisorDr K.S.Adam MurchMarch 2006 J - - - CONTENTS Subject Page -I - DedicationDedication........ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... I Acknowledgement ... '" ... ... ... ... ... ... '" ... ... ... ... '" ... '" ....... .. 11II Abstract ... ... ... '" ... ... ... '" ... ... ... ... -..... ... ... ... ... ... ..... III -I Ch-lch-1 DosimetryDosimefry - 1-1t-l IntroductionLntroduction . 1I - 1-2t-2 Principle of Dosimetry '" '" . 2 1-3l-3 DosimetryDosimefiySystems . 3J 1-3-1l-3-l primary standard dosimeters '" . 4 - 1-3-2l-3-Z Reference standard dosimeters ... .. " . 4 1-3-3L-3-3 Transfer standard dosimeters ... ... '" . 4 1-3-4t-3-4 Routine dosimeters . 5 1-4I-4 Measurement of absorbed dose . 6 1-5l-5 Calibration of DosimetryDosimetrvsystemsvstem '" . 6 1-6l-6 Transit dose effects . 8 Ch-2ch-2 Requirements of chemical dosimeters 2-12-l Introduction ... ... ... .............................................. 111l 2-2 Developing of chemical dosimeters ... ... .. ....... ... .. ..... 12t2 2-3 Classification of Dosimetry methods.methods .......................... 14l4 2-4 RequirementsRequiremsnts of ideal chemical dosimeters ,. ... 15 2-5 Types of chemical system .
    [Show full text]
  • The International Commission on Radiological Protection: Historical Overview
    Topical report The International Commission on Radiological Protection: Historical overview The ICRP is revising its basic recommendations by Dr H. Smith Within a few weeks of Roentgen's discovery of gamma rays; 1.5 roentgen per working week for radia- X-rays, the potential of the technique for diagnosing tion, affecting only superficial tissues; and 0.03 roentgen fractures became apparent, but acute adverse effects per working week for neutrons. (such as hair loss, erythema, and dermatitis) made hospital personnel aware of the need to avoid over- Recommendations in the 1950s exposure. Similar undesirable acute effects were By then, it was accepted that the roentgen was reported shortly after the discovery of radium and its inappropriate as a measure of exposure. In 1953, the medical applications. Notwithstanding these observa- ICRU recommended that limits of exposure should be tions, protection of staff exposed to X-rays and gamma based on consideration of the energy absorbed in tissues rays from radium was poorly co-ordinated. and introduced the rad (radiation absorbed dose) as a The British X-ray and Radium Protection Committee unit of absorbed dose (that is, energy imparted by radia- and the American Roentgen Ray Society proposed tion to a unit mass of tissue). In 1954, the ICRP general radiation protection recommendations in the introduced the rem (roentgen equivalent man) as a unit early 1920s. In 1925, at the First International Congress of absorbed dose weighted for the way different types of of Radiology, the need for quantifying exposure was radiation distribute energy in tissue (called the dose recognized. As a result, in 1928 the roentgen was equivalent in 1966).
    [Show full text]
  • MIRD Pamphlet No. 22 - Radiobiology and Dosimetry of Alpha- Particle Emitters for Targeted Radionuclide Therapy
    Alpha-Particle Emitter Dosimetry MIRD Pamphlet No. 22 - Radiobiology and Dosimetry of Alpha- Particle Emitters for Targeted Radionuclide Therapy George Sgouros1, John C. Roeske2, Michael R. McDevitt3, Stig Palm4, Barry J. Allen5, Darrell R. Fisher6, A. Bertrand Brill7, Hong Song1, Roger W. Howell8, Gamal Akabani9 1Radiology and Radiological Science, Johns Hopkins University, Baltimore MD 2Radiation Oncology, Loyola University Medical Center, Maywood IL 3Medicine and Radiology, Memorial Sloan-Kettering Cancer Center, New York NY 4International Atomic Energy Agency, Vienna, Austria 5Centre for Experimental Radiation Oncology, St. George Cancer Centre, Kagarah, Australia 6Radioisotopes Program, Pacific Northwest National Laboratory, Richland WA 7Department of Radiology, Vanderbilt University, Nashville TN 8Division of Radiation Research, Department of Radiology, New Jersey Medical School, University of Medicine and Dentistry of New Jersey, Newark NJ 9Food and Drug Administration, Rockville MD In collaboration with the SNM MIRD Committee: Wesley E. Bolch, A Bertrand Brill, Darrell R. Fisher, Roger W. Howell, Ruby F. Meredith, George Sgouros (Chairman), Barry W. Wessels, Pat B. Zanzonico Correspondence and reprint requests to: George Sgouros, Ph.D. Department of Radiology and Radiological Science CRB II 4M61 / 1550 Orleans St Johns Hopkins University, School of Medicine Baltimore MD 21231 410 614 0116 (voice); 413 487-3753 (FAX) [email protected] (e-mail) - 1 - Alpha-Particle Emitter Dosimetry INDEX A B S T R A C T.........................................................................................................................
    [Show full text]
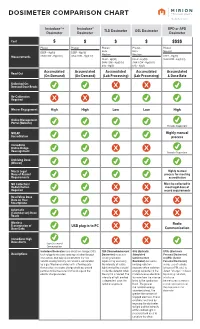
  • Dosimeter Comparison Chart
    DOSIMETER COMPARISON CHART Instadose®+ Instadose® EPD or APD TLD Dosimeter OSL Dosimeter Dosimeter Dosimeter Dosimeter Cost $ $ $ $$$$ Photon Photon Photon Photon Photon Beta Beta Neutron DEEP - Hp(10) DEEP - Hp(10) Neutron Neutron Measurements SHALLOW - Hp(0.07) SHALLOW - Hp(0.07) DEEP - Hp(10) DEEP - Hp(10) DEEP - Hp(10) SHALLOW - Hp(0.07) SHALLOW - Hp(0.07) SHALLOW - Hp(0.07) EYE - Hp(3) EYE - Hp(3) Read Out Accumulated Accumulated Accumulated Accumulated Accumulated (On-Demand) (On-Demand) (Lab Processing) (Lab Processing) & Dose Rate Unlimited On- Demand Dose Reads Re-Calibration Required Wearer Engagement High High Low Low High Online Management Portal (Website) Provider Dependent NVLAP Highly manual Accreditation process Immediate Online Badge Reassignment Provider Dependent Archiving Dose (Wearer) Meets Legal Highly manual Dose of Record process for meeting Requirements accreditation NO Collection/ Must be collected to Redistribution meet legal dose of Required record requirements Read/View Dose Data on Your Smartphone Automatic (Calendar-set) Dose Reads Wireless Radio Transmission of USB plug-in to PC Dose Data Communication Immediate High Dose Alerts Upon Successful Communication Instadose Dosimeters use direct ion storage (DIS) TLD (Thermoluminescent OSL (Optically EPDs (Electronic Descriptions technology to measure ionizing radiation through Dosimeter) measures Stimulated Personal Dosimeter) interactions that take place between the non- ionizing radiation Luminescence or APDs (Active volatile analog memory cell, which is surrounded exposure by assessing Dosimeter) measures Personal Dosimeter) by a gas filled ion chamber with a floating gate the intensity of visible ionizing radiation makes use of a diode that creates an electric charge enabling ionized light emitted by a crystal exposure when radiation (silicon or PIN, etc.) to particles to be measured by the change in the inside the detector when energy deposited in the detect “charges” induced electric charge created.
    [Show full text]
  • Site-Specific Calibration of the Hanford Personnel Neutron Dosimeter
    Gw^HI0n--7 PNL-SA-24010 SITE-SPECIFIC CALIBRATION OF THE HANFORD PERSONNEL NEUTRON DOSIMETER BEC 2 7 mm A. W. Endres Q o 7- L. W. Brackenbush ° f W. V. Baumgartner B. A. Rathbone October 1994 Presented at the Fourth Conference on Radiation Protection and Dosimetry October 23-27, 1994 Orlando, Florida Prepared for the U.S. Department of Energy under Contract DE-AC06-76RLO 1830 Pacific Northwest Laboratory Richland, Washington 99352 DISCLAIMER This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsi• bility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Refer• ence herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recom• mendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. MUM1TED 4STR1BUTION Or TH« DU^- to u G£ DISCLAIMER Portions of this document may be illegible in electronic image products. Images are produced from the best available original document. SITE-SPECIFIC CALIBRATION OF THE HANFORD PERSONNEL NEUTRON DOSIMETER A. W. Endres, L. W. Brackenbush, W. V. Baumgartner, and B. A. Rathbone Pacific Northwest Laboratory, Richland, Washington 99352 INTRODUCTION A new personnel dosimetry system, employing a standard Hanford thermo• luminescent dosimeter (TLD) and a combination dosimeter with both CR-39 nuclear track and TLD-albedo elements, is being implemented at Hanford.
    [Show full text]
  • Radiation Glossary
    Radiation Glossary Activity The rate of disintegration (transformation) or decay of radioactive material. The units of activity are Curie (Ci) and the Becquerel (Bq). Agreement State Any state with which the U.S. Nuclear Regulatory Commission has entered into an effective agreement under subsection 274b. of the Atomic Energy Act of 1954, as amended. Under the agreement, the state regulates the use of by-product, source, and small quantities of special nuclear material within said state. Airborne Radioactive Material Radioactive material dispersed in the air in the form of dusts, fumes, particulates, mists, vapors, or gases. ALARA Acronym for "As Low As Reasonably Achievable". Making every reasonable effort to maintain exposures to ionizing radiation as far below the dose limits as practical, consistent with the purpose for which the licensed activity is undertaken. It takes into account the state of technology, the economics of improvements in relation to state of technology, the economics of improvements in relation to benefits to the public health and safety, societal and socioeconomic considerations, and in relation to utilization of radioactive materials and licensed materials in the public interest. Alpha Particle A positively charged particle ejected spontaneously from the nuclei of some radioactive elements. It is identical to a helium nucleus, with a mass number of 4 and a charge of +2. Annual Limit on Intake (ALI) Annual intake of a given radionuclide by "Reference Man" which would result in either a committed effective dose equivalent of 5 rems or a committed dose equivalent of 50 rems to an organ or tissue. Attenuation The process by which radiation is reduced in intensity when passing through some material.
    [Show full text]
  • External and Internal Dosimetry
    Chapter 7 External and Internal Dosimetry H-117 – Introductory Health Physics Slide 1 Objectives ¾ Discuss factors influencing external and internal doses ¾ Define terms used in external dosimetry ¾ Discuss external dosimeters such as TLDs, film badges, OSL dosimeters, pocket chambers, and electronic dosimetry H-117 – Introductory Health Physics Slide 2 Objectives ¾ Define terms used in internal dosimetry ¾ Discuss dose units and limits ¾ Define the ALI, DAC and DAC-hr ¾ Discuss radiation signs and postings H-117 – Introductory Health Physics Slide 3 Objectives ¾ Discuss types of bioassays ¾ Describe internal dose measuring equipment and facilities ¾ Discuss principles of internal dose calculation and work sample problems H-117 – Introductory Health Physics Slide 4 External Dosimetry H-117 – Introductory Health Physics Slide 5 External Dosimetry Gamma, beta or neutron radiation emitted by radioactive material outside the body irradiates the skin, lens of the eye, extremities & the whole body (i.e. internal organs) H-117 – Introductory Health Physics Slide 6 External Dosimetry (cont.) ¾ Alpha particles cannot penetrate the dead layer of skin (0.007 cm) ¾ Beta particles are primarily a skin hazard. However, energetic betas can penetrate the lens of an eye (0.3 cm) and deeper tissue (1 cm) ¾ Beta sources can produce more penetrating radiation through bremsstrahlung ¾ Primary sources of external exposure are photons and neutrons ¾ External dose must be measured by means of appropriate dosimeters H-117 – Introductory Health Physics Slide 7
    [Show full text]
  • TLD) Service PROTECT YOURSELF and YOUR EMPLOYEES!
    Thermoluminescent Dosimetry (TLD) Service PROTECT YOURSELF AND YOUR EMPLOYEES! About Us PL Medical Co., LLC, offers TLD dosimeters which are based on state-of-the-art technology. PL Medical Co., LLC supplies accredited dosimetry services to industries in which radiation monitoring is desired or mandated by state and/or federal regulatory standards. PL Medical Co., LLC is accredited to provide dosimetry services by the National Voluntary Laboratory Accreditation Program (NVLAP), a division of National Institute of Standards and Technology (NIST). Advantages • Access to myTLDaccount • No account maintenance or set-up fees Applications • One control badge provided free of charge • Primary Care • Flexibility of the wear period •EMS • Automatic dosimeter replacement every three months •Podiatry for one year • Occupational Health • A reply envelope to return badges • Corrections • Computer generated reports sent to the customer • Orthopedics within 2-3 weeks of receiving the dosimeters (exposure • Homeland Security history automatically updated) • X-Ray Technicians • Advance notice not required for cancellation. Prompt •Hospitals credit for termination of service of an employee • Universities and National Laboratories • Each dose report is reviewed to check if it meets • Dentists ALARA limits •Chiropractors • Customer care – you will always be in contact with a • Veterinary “live person” Logistics of Service Product Description • An order is placed at http://manageTLD.plmedical.com • Possible wear period of up to twelve months or by phoning,
    [Show full text]
  • Emergency and Combat First Aid» Module № 1 Emergency and Combat First Aid Topic 7 Means of Mass Destruction
    Ministry of Health of Ukraine Ukrainian Medical stomatological Academy It is ratified On meeting department Of accident aid and military medicine «___»_____________20 __y. Protocol №_____ Manager of department DMSc ., assistant professor __________К.Shepitko METHODICAL INSTRUCTION FOR INDEPENDENT WORK OF STUDENTS DURING PREPARATIONS FOR THE PRACTICAL LESSON Educational discipline «Emergency and Combat First Aid» Module № 1 Emergency and Combat First Aid Topic 7 Means of Mass Destruction. First Aid. Weapons of mass destructions. Lesson 10 Radiations chemical accidents .First Aid Сourse ІІ Foreing students training dentistry Faculty Training of specialists of the second (master) level of higher of education (название уровня высшего образования) Areas of knowledge _______ 22 «Health protection»_________ (шифр и название области знаний) Specialty ________222 «Medicine», 221 «Stomatology»________________ (код и наименование специальности) Poltava 2019 The relevance of the topic: Military action in modern warfare will be carried out with high activity and limit tension. They cause great losses in the army and among the population, the destruction of potentially dangerous objects, energy centers, waterworks, the formation of large zones of destruction, fires and floods. The main form of countering in the war, is armed struggle - the organized use of armed forces and weapons to achieve specific political and military objectives, a combination of military actions of varying scales. To conventional weapons, the application of which may cause losses among the population are missiles and aerial munitions, including precision munitions volumetric detonation of cluster and incendiary. Have the greatest efficiency high precision conventional weapons, which provide automatic detection and reliable destruction of targets and enemy targets with a single shot (trigger).
    [Show full text]