DOCSLIB.ORG

Towards a Generative Framework for Understanding Musical Modes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Towards a Generative Framework for Understanding Musical Modes Table of Contents Introduction & Key Terms................................................................................1 Chapter I. Heptatonic Modes.............................................................................3 Section 1.1: The Church Mode Set..............................................................3 Section 1.2: The Melodic Minor Mode Set...................................................10 Section 1.3: The Neapolitan Mode Set........................................................16 Section 1.4: The Harmonic Major and Minor Mode Sets...................................21 Section 1.5: The Harmonic Lydian, Harmonic Phrygian, and Double Harmonic Mode Sets..................................................................26 Chapter II. Pentatonic Modes..........................................................................29 Section 2.1: The Pentatonic Church Mode Set...............................................29 Section 2.2: The Pentatonic Melodic Minor Mode Set......................................34 Chapter III. Rhythmic Modes..........................................................................40 Section 3.1: Rhythmic Modes in a Twelve-Beat Cycle.....................................40 Section 3.2: Rhythmic Modes in a Sixteen-Beat Cycle.....................................41 Applications of the Generative Modal Framework..................................................45 Bibliography.............................................................................................46 O1 O Introduction Western musicians, composers, and music theorists have explored the concept of modal- ity since antiquity. From ancient Greek music to modern jazz, modes have played an important and diverse array of roles in a myriad of Western musical traditions and genres. Studies in the psychology of music perception have shown that the variable of mode correlates with Western listeners’ perception of emotional meaning in music, and that this correlation is significant for both musicians and nonmusicians.1 Despite the prevalence of modality in Western music, no extant music theory text offers a comprehensive and accessible delineation of the mathematical patterns found in musical modes. Although music theorists and mathematicians have explored the world of modes in the language of formal logic and set theory, musicians and composers have been largely (and regrettably) excluded from these fascinating discussions due to the advanced technical language employed therein. When creators of music are shut out from discussions about music, however abstract, entire veins of potential for artistic innovation are inevitably left unexplored. The purpose of this paper is to introduce a musically literate (but not necessarily mathematically literate) audience to a colorful world of advanced modal concepts by presenting these concepts clearly and thoroughly in the language of Western music theory. Fundamentally, the generative modal framework outlined in this paper is a procedural framework for generating new rhythmic and tonal possibilities—in the form of mode sets and supersets—through pattern recognition, recombination, and analogy. This framework does not suggest a universal underlying musical grammar similar to the universal grammar proposed in Noam Chomsky’s linguistic theory of generative grammar. The generative modal framework has little to do with musical grammar, except insofar as it assumes equal spacing of pitches and beats. It is neither a prescriptive nor descriptive account of any culture- or genre-specific use of modes. Rather, this framework is intended to shed light on a series of beautiful mathematically-based rhythmic and tonal resources for musicians and composers to add to their musical vocabularies and use at their discretion. Most importantly, a complete understanding of the framework must include knowledge of how to use its techniques to generate and explore new rhythmic and tonal resources on one’s own. The countless potential applications of the procedural framework outlined in this paper are far from exhausted in the discussions that follow, as this paper aims only to point the way towards a generative framework for understanding musical modes. The vast majority of musical material available through the framework lies outside the scope of this paper, and the reader is encouraged to explore these many avenues using the tools and techniques outlined in the follow- ing chapters. 1 D. Ramos, J. L. O. Bueno, and E. Bigand, "Manipulating Greek Musical Modes and Tempo Affects Perceived Musical Emotion in Musicians and Nonmusicians," Brazilian Journal of Medical and Biological Research 44, no. 2 (February 2011): 165-72. 2 Key Terms Validity In this paper, the term valid applies to any scale all of whose scale degrees are enhar- monically distinct. All common scales in Western music are valid. The scale spelled 1-2-3-♯4-♭5- 6-7 is an example of an invalid scale. This scale’s fourth and fifth scale degrees are enhar- monically equivalent, rendering the scale essentially a six-tone (hexatonic) scale written as a seven-tone (heptatonic) scale. The concept of validity applies only to scales in twelve-tone equal temperament (12ET). Scale, scale family, mode, and mode set The word scale denotes a set of pitches identified by their intervallic relationship to a tonic pitch. The scale family of scale s is the set of every valid scale of a particular size (e.g. heptatonic) that contains every pitch in s. For example, the heptatonic scale family for the scale spelled 1-2-3-4-5 consists of the scales 1-2-3-4-5-6-7, 1-2-3-4-5-6-♭7, 1-2-3-4-5-♭6-7, and 1-2-3- 4-5-♭6-♭7, or Ionian, Mixolydian, Harmonic major, and Melodic major, respectively. ♭6-7♭ ♭Ionian♭ ♭6-♭7♭ ♭Mixolydian♭ ♭♭6-7♭ ♭Harmonic major♭ ♭♭6-♭7♭ ♭Melodic major♭ Table 0.1. The 1-2-3-4-5 heptatonic scale family. The term mode set denotes a set of scales that all share the same interval structure yet all have a different tonic pitch. The word mode refers to an individual scale within a mode set. Other Notes About Terminology Most mode sets are named after a particular mode contained within the set. In general, the first letter of the names of specific modes (e.g. Melodic minor, Harmonic major) is capitalized, while the first letter of the names of mode sets (e.g. melodic minor mode set, harmonic major mode set) is lowercase. Because absolute pitch values are irrelevant to the generative modal framework, the cycle of fifths is represented here using scale degrees instead of note names, so that C becomes 1, D becomes 2, A♭ becomes ♭6, and so on. Interval structures in this paper are written in ascending order using numerals, where 1 indicates a half step, 2 a whole step, 3 a minor third, and so on. For example, the interval structure of the natural minor (Aeolian) scale is 2122122. 3 I. Heptatonic Modes This chapter will cover the derivation of a series of four generations of heptatonic mode sets in 12ET, starting with the most ubiquitous mode set in Western music—the diatonic church mode set—and moving on to increasingly rarer, more jagged mode sets. We can visualize this “family” of mode sets as a family tree: Figure 1.0.1. The first four generations in the 12ET heptatonic/pentatonic modal family tree. While this particular visualization applies only to heptatonic and pentatonic mode sets in 12ET, the reasoning behind it can be applied to mode sets of any size in any equal-tempered tuning system (or, in the case of rhythmic modes, any equally-subdivided beat cycle—more on this in Chapter III). Although only four generations are shown here, a theoretically infinite number of generations can be derived using the methods introduced in the following sections. 1.1. The Church Mode Set The advantage of beginning our exploration of the generative framework with the church mode set lies not only in its familiarity to most Western musicians, but also in two different ways it can be plucked directly out of the framework of 12ET: stacked fifths and maximal evenness. 4 By starting on the tonic and traversing the cycle of fifths clockwise until seven scale degrees are covered, we obtain the scale degree set 1-5-2-6-3-7-♯4. In ascending numerical order, 1-2-3-♯4- 5-6-7 spells Lydian. Figure 1.1.1. Derivation of Lydian by stacked fifths. Conversely, by starting on the tritone and traversing the cycle of fifths clockwise until seven scale degrees are covered, we obtain the scale degree set ♭5-♭2-♭6-♭3-4-♭7-1. In ascending numerical order, 1-♭2-♭3-4-♭5-♭6-♭7 spells Locrian. Figure 1.1.2. Derivation of Locrian by stacked fifths. 5 The same method can be used to derive the other five church modes simply by shifting the initial and final scale degree: Figure 1.1.3. Derivation of Ionian, Mixolydian, and Dorian by stacked fifths. 6 Figure 1.1.4. Derivation of Aeolian and Phrygian by stacked fifths. Numerous theorists have pointed out the possibility of deriving of the church mode set— particularly the Lydian mode—by stacked fifths. Most prominently, George Russell used this derivation as the foundation of his Lydian Chromatic Concept of Tonal Organization, one of the most influential jazz theory texts of all time.2 In x-tone equal temperament, where x is any positive integer, the precise frequency ratio f(n) of the nth interval in the chromatic scale is given by the following formula: f(n) = 2n/x For example, the frequency ratio of the seventh interval in 12ET (the 12ET approximation of a just perfect fifth with frequency ratio 1.5) is 27/12, or approximately 1.498. By comparing
Load more

Recommended publications
  • 4. Non-Heptatonic Modes
    Tagg: Everyday Tonality II — 4. Non‐heptatonic modes 151 4. Non‐heptatonic modes If modes containing seven different scale degrees are heptatonic, eight‐note modes are octatonic, six‐note modes hexatonic, those with five pentatonic, while four‐ and three‐note modes are tetratonic and tritonic. Now, even though the most popular pentatonic modes are sometimes called ‘gapped’ because they contain two scale steps larger than those of the ‘church’ modes of Chapter 3 —doh ré mi sol la and la doh ré mi sol, for example— they are no more incomplete FFBk04Modes2.fm. 2014-09-14,13:57 or empty than the octatonic start to example 70 can be considered cluttered or crowded.1 Ex. 70. Vigneault/Rochon (1973): Je chante pour (octatonic opening phrase) The point is that the most widespread convention for numbering scale degrees (in Europe, the Arab world, India, Java, China, etc.) is, as we’ve seen, heptatonic. So, when expressions like ‘thirdless hexatonic’ occur in this chapter it does not imply that the mode is in any sense deficient: it’s just a matter of using a quasi‐global con‐ vention to designate a particular trait of the mode. Tritonic and tetratonic Tritonic and tetratonic tunes are common in many parts of the world, not least in traditional music from Micronesia and Poly‐ nesia, as well as among the Māori, the Inuit, the Saami and Native Americans of the great plains.2 Tetratonic modes are also found in Christian psalm and response chanting (ex. 71), while the sound of children chanting tritonic taunts can still be heard in playgrounds in many parts of the world (ex.
    [Show full text]
  • View Printable PDF of 4.2 the Modes of Minor
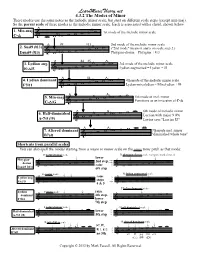
    LearnMusicTheory.net 4.3.2 The Modes of Minor These modes use the same notes as the melodic minor scale, but start on different scale steps (except min-maj). So the parent scale of these modes is the melodic minor scale. Each is associated with a chord, shown below. 1. Min-maj 1st mode of the melodic minor scale C- w wmw ^ & w wmbw w w b9 §13 2nd mode of the melodic minor scale 2. Susb9 (§13) wmw w ("2nd mode" means it starts on scale step 2.) Dsusb9 (§13) & wmbw w w w Phrygian-dorian = Phyrgian + §13 #4 #5 3. Lydian aug. mbw 3rd mode of the melodic minor scale wmw w Lydian augmented = Lydian + #5 Eb ^ #5 & bw w w w #4 4. Lydian dominant 4th mode of the melodic minor scale w wmbw w F7#11 & w w w wm Lydian-mixolydian = Mixolydian + #4 5. Min-maj w w 5th mode of mel. minor wmw wmbw Functions as an inversion of C- C- ^ /G & w w ^ 6th mode of melodic minor 6. Half-diminished w w m w wmbw w Locrian with major 9 (§9) A-7b5 (§9) & w w Levine says "Locrian #2" w 7. Altered dominant wmbw w w w 7th mode mel. minor B7alt & wm w "diminished whole tone" Shortcuts from parallel scales You can also spell the modes starting from a major or minor scale on the same tonic pitch as that mode: D natural minor scale D phrygian-dorian scale (compare marked notes) lower Phrygian- I I 2nd step, I I dorian w bw w w raise _ w nw w w Dsusb9 (§13) & w w w _ & bw w w w 6th step _ w Eb major scale Eb lydian augmented scale Lydian aug.
    [Show full text]
  • James Clerk Maxwell
    James Clerk Maxwell JAMES CLERK MAXWELL Perspectives on his Life and Work Edited by raymond flood mark mccartney and andrew whitaker 3 3 Great Clarendon Street, Oxford, OX2 6DP, United Kingdom Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship, and education by publishing worldwide. Oxford is a registered trade mark of Oxford University Press in the UK and in certain other countries c Oxford University Press 2014 The moral rights of the authors have been asserted First Edition published in 2014 Impression: 1 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by licence or under terms agreed with the appropriate reprographics rights organization. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above You must not circulate this work in any other form and you must impose this same condition on any acquirer Published in the United States of America by Oxford University Press 198 Madison Avenue, New York, NY 10016, United States of America British Library Cataloguing in Publication Data Data available Library of Congress Control Number: 2013942195 ISBN 978–0–19–966437–5 Printed and bound by CPI Group (UK) Ltd, Croydon, CR0 4YY Links to third party websites are provided by Oxford in good faith and for information only.
    [Show full text]
  • THE MODES of ANCIENT GREECE by Elsie Hamilton
    THE MODES OF ANCIENT GREECE by Elsie Hamilton * * * * P R E F A C E Owing to requests from various people I have consented with humility to write a simple booklet on the Modes of Ancient Greece. The reason for this is largely because the monumental work “The Greek Aulos” by Kathleen Schlesinger, Fellow of the Institute of Archaeology at the University of Liverpool, is now unfortunately out of print. Let me at once say that all the theoretical knowledge I possess has been imparted to me by her through our long and happy friendship over many years. All I can claim as my own contribution is the use I have made of these Modes as a basis for modern composition, of which details have been given in Appendix 3 of “The Greek Aulos”. Demonstrations of Chamber Music in the Modes were given in Steinway Hall in 1917 with the assistance of some of the Queen’s Hall players, also 3 performances in the Etlinger Hall of the musical drama “Sensa”, by Mabel Collins, in 1919. A mime “Agave” was performed in the studio of Madame Matton-Painpare in 1924, and another mime “The Scorpions of Ysit”, at the Court Theatre in 1929. In 1935 this new language of Music was introduced at Stuttgart, Germany, where a small Chamber Orchestra was trained to play in the Greek Modes. Singers have also found little difficulty in singing these intervals which are not those of our modern well-tempered system, of which fuller details will be given later on in this booklet.
    [Show full text]
  • Electrophonic Musical Instruments
    G10H CPC COOPERATIVE PATENT CLASSIFICATION G PHYSICS (NOTES omitted) INSTRUMENTS G10 MUSICAL INSTRUMENTS; ACOUSTICS (NOTES omitted) G10H ELECTROPHONIC MUSICAL INSTRUMENTS (electronic circuits in general H03) NOTE This subclass covers musical instruments in which individual notes are constituted as electric oscillations under the control of a performer and the oscillations are converted to sound-vibrations by a loud-speaker or equivalent instrument. WARNING In this subclass non-limiting references (in the sense of paragraph 39 of the Guide to the IPC) may still be displayed in the scheme. 1/00 Details of electrophonic musical instruments 1/053 . during execution only {(voice controlled (keyboards applicable also to other musical instruments G10H 5/005)} instruments G10B, G10C; arrangements for producing 1/0535 . {by switches incorporating a mechanical a reverberation or echo sound G10K 15/08) vibrator, the envelope of the mechanical 1/0008 . {Associated control or indicating means (teaching vibration being used as modulating signal} of music per se G09B 15/00)} 1/055 . by switches with variable impedance 1/0016 . {Means for indicating which keys, frets or strings elements are to be actuated, e.g. using lights or leds} 1/0551 . {using variable capacitors} 1/0025 . {Automatic or semi-automatic music 1/0553 . {using optical or light-responsive means} composition, e.g. producing random music, 1/0555 . {using magnetic or electromagnetic applying rules from music theory or modifying a means} musical piece (automatically producing a series of 1/0556 . {using piezo-electric means} tones G10H 1/26)} 1/0558 . {using variable resistors} 1/0033 . {Recording/reproducing or transmission of 1/057 . by envelope-forming circuits music for electrophonic musical instruments (of 1/0575 .
    [Show full text]
  • Orientalism As Represented in the Selected Piano Works by Claude Debussy
    Chapter 4 ORIENTALISM AS REPRESENTED IN THE SELECTED PIANO WORKS BY CLAUDE DEBUSSY A prominent English scholar of French music, Roy Howat, claimed that, out of the many composers who were attracted by the Orient as subject matter, “Debussy is the one who made much of it his own language, even identity.”55 Debussy and Hahn, despite being in the same social circle, never pursued an amicable relationship.56 Even while keeping their distance, both composers were somewhat aware of the other’s career. Hahn, in a public statement from 1890, praised highly Debussy’s musical artistry in L'Apres- midi d'un faune.57 Debussy’s Exposure to Oriental Cultures Debussy’s first exposure to oriental art and philosophy began at Mallarmé’s Symbolist gatherings he frequented in 1887 upon his return to Paris from Rome.58 At the Universal Exposition of 1889, he had his first experience in the theater of Annam (Vietnam) and the Javanese Gamelan orchestra (Indonesia), which is said to be a catalyst 55Roy Howat, The Art of French Piano Music: Debussy, Ravel, Fauré, Chabrier (New Haven, Conn.: Yale University Press, 2009), 110 56Gavoty, 142. 57Ibid., 146. 58François Lesure and Roy Howat. "Debussy, Claude." In Grove Music Online. Oxford Music Online, http://www.oxfordmusiconline.com/subscriber/article/grove/music/07353 (accessed April 4, 2011). 33 34 in his artistic direction. 59 In 1890, Debussy was acquainted with Edmond Bailly, esoteric and oriental scholar, who took part in publishing and selling some of Debussy’s music at his bookstore L’Art Indépendeant. 60 In 1902, Debussy met Louis Laloy, an ethnomusicologist and music critic who eventually became Debussy’s most trusted friend and encouraged his use of Oriental themes.61 After the Universal Exposition in 1889, Debussy had another opportunity to listen to a Gamelan orchestra 11 years later in 1900.
    [Show full text]
  • I. the Term Стр. 1 Из 93 Mode 01.10.2013 Mk:@Msitstore:D
    Mode Стр. 1 из 93 Mode (from Lat. modus: ‘measure’, ‘standard’; ‘manner’, ‘way’). A term in Western music theory with three main applications, all connected with the above meanings of modus: the relationship between the note values longa and brevis in late medieval notation; interval, in early medieval theory; and, most significantly, a concept involving scale type and melody type. The term ‘mode’ has always been used to designate classes of melodies, and since the 20th century to designate certain kinds of norm or model for composition or improvisation as well. Certain phenomena in folksong and in non-Western music are related to this last meaning, and are discussed below in §§IV and V. The word is also used in acoustical parlance to denote a particular pattern of vibrations in which a system can oscillate in a stable way; see Sound, §5(ii). For a discussion of mode in relation to ancient Greek theory see Greece, §I, 6 I. The term II. Medieval modal theory III. Modal theories and polyphonic music IV. Modal scales and traditional music V. Middle East and Asia HAROLD S. POWERS/FRANS WIERING (I–III), JAMES PORTER (IV, 1), HAROLD S. POWERS/JAMES COWDERY (IV, 2), HAROLD S. POWERS/RICHARD WIDDESS (V, 1), RUTH DAVIS (V, 2), HAROLD S. POWERS/RICHARD WIDDESS (V, 3), HAROLD S. POWERS/MARC PERLMAN (V, 4(i)), HAROLD S. POWERS/MARC PERLMAN (V, 4(ii) (a)–(d)), MARC PERLMAN (V, 4(ii) (e)–(i)), ALLAN MARETT, STEPHEN JONES (V, 5(i)), ALLEN MARETT (V, 5(ii), (iii)), HAROLD S. POWERS/ALLAN MARETT (V, 5(iv)) Mode I.
    [Show full text]
  • Studies in Instrumentation and Orchestration and in the Recontextualisation of Diatonic Pitch Materials (Portfolio of Compositions)
    Studies in Instrumentation and Orchestration and in the Recontextualisation of Diatonic Pitch Materials (Portfolio of Compositions) by Chris Paul Harman Submitted to The University of Birmingham for the degree of DOCTOR OF PHILOSOPHY Department of Music School of Humanities The University of Birmingham September 2011 University of Birmingham Research Archive e-theses repository This unpublished thesis/dissertation is copyright of the author and/or third parties. The intellectual property rights of the author or third parties in respect of this work are as defined by The Copyright Designs and Patents Act 1988 or as modified by any successor legislation. Any use made of information contained in this thesis/dissertation must be in accordance with that legislation and must be properly acknowledged. Further distribution or reproduction in any format is prohibited without the permission of the copyright holder. Abstract: The present document examines eight musical works for various instruments and ensembles, composed between 2007 and 2011. Brief summaries of each work’s program are followed by discussions of instrumentation and orchestration, and analysis of pitch organization. Discussions of instrumentation and orchestration explore the composer’s approach to diversification of instrumental ensembles by the inclusion of non-orchestral instruments, and redefinition of traditional hierarchies among instruments in a standard ensemble or orchestral setting. Analyses of pitch organization detail various ways in which the composer renders diatonic
    [Show full text]
  • Chromatic Sequences
    CHAPTER 30 Melodic and Harmonic Symmetry Combine: Chromatic Sequences Distinctions Between Diatonic and Chromatic Sequences Sequences are paradoxical musical processes. At the surface level they provide rapid harmonic rhythm, yet at a deeper level they function to suspend tonal motion and prolong an underlying harmony. Tonal sequences move up and down the diatonic scale using scale degrees as stepping-stones. In this chapter, we will explore the consequences of transferring the sequential motions you learned in Chapter 17 from the asymmetry of the diatonic scale to the symmetrical tonal patterns of the nineteenth century. You will likely notice many similarities of behavior between these new chromatic sequences and the old diatonic ones, but there are differences as well. For instance, the stepping-stones for chromatic sequences are no longer the major and minor scales. Furthermore, the chord qualities of each individual harmony inside a chromatic sequence tend to exhibit more homogeneity. Whereas in the past you may have expected major, minor, and diminished chords to alternate inside a diatonic sequence, in the chromatic realm it is not uncommon for all the chords in a sequence to manifest the same quality. EXAMPLE 30.1 Comparison of Diatonic and Chromatic Forms of the D3 ("Pachelbel") Sequence A. 624 CHAPTER 30 MELODIC AND HARMONIC SYMMETRY COMBINE 625 B. Consider Example 30.1A, which contains the D3 ( -4/ +2)-or "descending 5-6"-sequence. The sequence is strongly goal directed (progressing to ii) and diatonic (its harmonies are diatonic to G major). Chord qualities and distances are not consistent, since they conform to the asymmetry of G major.
    [Show full text]
  • Mode Handout Without Examples
    The 24 Essential Mode/Chord Structures Modes & Symbols of the Major Scale MAJOR SCALE MODE FORMULA I: MAJOR SCALE MODE SYMBOL I: 1-1(1) – IONIAN ma13 EXAMPLES: In the Key of C: C-C(C) With C as the Root: C-C(C) MAJOR SCALE FORMULA II: MAJOR SCALE MODE SYMBOL II: 2-2(1) – DORIAN mi13 EXAMPLES: In the Key of C: D-D(C) With C as the Root: C-C(Bb) MAJOR SCALE FORMULA III: MAJOR SCALE MODE SYMBOL III: 3-3(1) – PHRYGIAN mi11(b9,b13) EXAMPLES: In the Key of C: E-E(C) With C as the Root: C-C(Ab) MAJOR SCALE FORMULA IV: MAJOR SCALE MODE SYMBOL IV: 4-4(1) – LYDIAN ma13(#11) EXAMPLES: In the Key of C: F-F(C) With C as the Root: C-C(G) MAJOR SCALE FORMULA V: MAJOR SCALE MODE SYMBOL V: 5-5(1) – MIXOLYDIAN 13 EXAMPLES: In the Key of C: G-G(C) With C as the Root: C-C(F) MAJOR SCALE FORMULA VI: MAJOR SCALE MODE SYMBOL VI: 6-6(1) – AEOLIAN mi11(b13) EXAMPLES: In the Key of C: A-A(C) With C as the Root: C-C(Eb) MAJOR SCALE FORMULA VII: MAJOR SCALE MODE SYMBOL VII: 7-7(1) – LOCRIAN mi11(b5,b9,b13) EXAMPLES: In the Key of C: B-B(C) With C as the Root: C-C(Db) Modes & Symbols of the Melodic Minor Scale MELODIC MINOR FORMULA I: MELODIC MINOR SCALE MODE SYMBOL I: 1-1(1mm) – MELODIC MINOR mi(ma13) EXAMPLES: In the Key of Cmm: C-C(Cmm) With C as the Root: C-C(Cmm) MELODIC MINOR FORMULA II: MELODIC MINOR SCALE MODE SYMBOL II: 2-2(1mm) – DORIAN b2 Mi13(b9) EXAMPLES: In the Key of Cmm: D-D(Cmm) With C as the Root: C-C(Bbmm) MELODIC MINOR FORMULA III: MELODIC MINOR SCALE MODE SYMBOL III: 3-3(1mm) – LYDIAN AUGMENTED +ma13(#11) EXAMPLES: In the Key of Cmm: Eb-Eb(Cmm)
    [Show full text]
  • Proquest Dissertations
    A comparison of embellishments in performances of bebop with those in the music of Chopin Item Type text; Thesis-Reproduction (electronic) Authors Mitchell, David William, 1960- Publisher The University of Arizona. Rights Copyright © is held by the author. Digital access to this material is made possible by the University Libraries, University of Arizona. Further transmission, reproduction or presentation (such as public display or performance) of protected items is prohibited except with permission of the author. Download date 03/10/2021 23:23:11 Link to Item http://hdl.handle.net/10150/278257 INFORMATION TO USERS This manuscript has been reproduced from the miaofillm master. UMI films the text directly fi^om the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be fi-om any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand corner and contLDuing from left to right in equal sections with small overlaps. Each original is also photographed in one exposure and is included in reduced form at the back of the book.
    [Show full text]
  • Technical Analysis on HW Ernst's Six Etudes for Solo Violin in Multiple
    Technical Analysis on Heinrich Wilhelm Ernst’s Six Etudes for Solo Violin in Multiple Voices In partial fulfillment of the requirements for the degree of DOCTOR OF MUSICAL ARTS in the Performance Studies Division of the College-Conservatory of Music Violin by Shang Jung Lin M.M. The Boston Conservatory November 2019 Committee Chair: Won-Bin Yim, D.M.A. Abstract Heinrich Wilhelm Ernst was a Moravian violinist and composer who lived between 1814-1865. He was a friend of Brahms, collaborator with Mendelssohn, and was admired by Berlioz and Joachim. He was known as a violin virtuoso and composed many virtuosic works including an arrangement of Schubert’s Erlkönig for solo violin. The focus of this document will be on his Six Etudes for Solo Violin in Multiple Voices (also known as the Six Polyphonic Etudes). These pieces were published without opus number around 1862-1864. The etudes combine many different technical challenges with musical sensitivity. They were so difficult that the composer never gave a public performance of them. No. 6 is the most famous of the set, and has been performed by soloists in recent years. Ernst takes the difficulty level to the extreme and combines different layers of techniques within one hand. For example, the second etude has a passage that combines chords and left-hand pizzicato, and the sixth etude has a passage that combines harmonics with double stops. Etudes from other composers might contain these techniques but not simultaneously. The polyphonic nature allows for this layering of difficulties in Ernst’s Six Polyphonic Etudes.
    [Show full text]