Power Area Density in Inverse Spectra
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

HP Indigo 7K Digital Press Press Digital 7K Indigo HP The
Add premium HP Indigo printing and watch your business grow. business your watch and printing Indigo HP premium Add ONE PRESS, ENDLESS OPPORTUNITIES. ENDLESS PRESS, ONE truly robust press. robust truly volumes day in, day out with this this with out day in, day volumes offset-matching quality and high high and quality offset-matching automated tools while printing printing while tools automated Simplify production with smart, smart, with production Simplify and over 20 specialty inks. inks. specialty 20 over and the widest range of media media of range widest the and customer satisfaction—with satisfaction—with customer and enables endless applications— endless enables The HP Indigo 7K Digital Press Press Digital 7K Indigo HP The HP Indigo 7K Digital Press Technical specifications Printing speed 120 four-color 8.5 x 11 (A4) pages per minute - two-up 160 color 8.5 x 11 (A4) pages per minute in EPM - two-up 240 two-color or monochrome 8.5 x 11 (A4) pages per minute - two-up Image resolution 812 dpi at 8 bit; addressability: 2438 x 2438 dpi HDI (High Definition Imaging) Line screens 144, 160, 175, 180, 180m, 210, HMF200 lpi Sheet size 13 x 19 in (330 x 482 mm) maximum Image size 12.48 x 18.26 in (317 x 464 mm) maximum Paper weight and thickness* Coated: 55 lb text to 130 lb cover (80 to 350 gsm); Uncoated: 40 lb text to 130 lb cover (60 to 350 gsm); Thickness 3 to 16 pt. (70 to 400 microns) Feeder Four drawers: Three drawers with 6 in (150 mm) each, 1500 sheets of 80 lb text (120 gsm) each One special jobs drawer: 2.5 in (70mm), 700 sheets of 80 lb text, (700 sheets of 120 gsm) A total of 5200 sheets of 80 lb text (120 gsm). -

Comparing Levels of Crosstalk with Red/Cyan, Blue/Yellow, and Green
A. J. Woods, C. R. Harris, “Comparing levels of crosstalk with red/cyan, blue/yellow, and green/magenta anaglyph 3D glasses” in Proceedings of SPIE Stereoscopic Displays and Applications XXI, vol. 7253, pp. 0Q1-0Q12, January 2010. Online: www.cmst.curtin.edu.au Comparing levels of crosstalk with red/cyan, blue/yellow, and green/magenta anaglyph 3D glasses Andrew J. Woods*, Chris R. Harris Centre for Marine Science and Technology, Curtin University of Technology, GPO Box U1987, Perth WA 6845, Australia ABSTRACT The Anaglyph 3D method of stereoscopic visualization is both cost effective and compatible with all full-color displays, however this method often suffers from poor 3D image quality due to poor color quality and ghosting (whereby each eye sees a small portion of the perspective image intended for the other eye). Ghosting, also known as crosstalk, limits the ability of the brain to successfully fuse the images perceived by each eye and thus reduces the perceived quality of the 3D image. This paper describes a research project which has simulated the spectral performance of a wide selection of anaglyph 3D glasses on CRT, LCD and plasma displays in order to predict ghosting levels. This analysis has included for the first time a comparison of crosstalk between different color-primary types of anaglyph glasses - green/magenta and blue/yellow as well as the more traditional red/cyan. Sixteen pairs of anaglyph 3D glasses were simulated (6 pairs of red/cyan glasses, 6 pairs of blue/yellow glasses and 4 pairs of green/magenta glasses). The spectral emission results for 13 LCDs, 15 plasma displays and one CRT Monitor were used for the analysis. -

R Color Cheatsheet
R Color Palettes R color cheatsheet This is for all of you who don’t know anything Finding a good color scheme for presenting data about color theory, and don’t care but want can be challenging. This color cheatsheet will help! some nice colors on your map or figure….NOW! R uses hexadecimal to represent colors TIP: When it comes to selecting a color palette, Hexadecimal is a base-16 number system used to describe DO NOT try to handpick individual colors! You will color. Red, green, and blue are each represented by two characters (#rrggbb). Each character has 16 possible waste a lot of time and the result will probably not symbols: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F: be all that great. R has some good packages for color palettes. Here are some of the options “00” can be interpreted as 0.0 and “FF” as 1.0 Packages: grDevices and i.e., red= #FF0000 , black=#000000, white = #FFFFFF grDevices colorRamps palettes Two additional characters (with the same scale) can be grDevices comes with the base cm.colors added to the end to describe transparency (#rrggbbaa) installation and colorRamps topo.colors terrain.colors R has 657 built in color names Example: must be installed. Each palette’s heat.colors To see a list of names: function has an argument for rainbow colors() peachpuff4 the number of colors and see P. 4 for These colors are displayed on P. 3. transparency (alpha): options R translates various color models to hex, e.g.: heat.colors(4, alpha=1) • RGB (red, green, blue): The default intensity scale in R > #FF0000FF" "#FF8000FF" "#FFFF00FF" "#FFFF80FF“ ranges from 0-1; but another commonly used scale is 0- 255. -
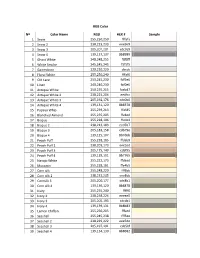
RGB Color Nº Color Name RGB HEX # Sample 1 Snow 255,250,250
RGB Color Nº Color Name RGB HEX # Sample 1 Snow 255,250,250 fffafa 2 Snow 2 238,233,233 eee9e9 3 Snow 3 205,201,201 cdc9c9 4 Snow 4 139,137,137 8b8989 5 Ghost White 248,248,255 f8f8ff 6 White Smoke 245,245,245 f5f5f5 7 Gainesboro 220,220,220 dccdc 8 Floral White 255,250,240 fffaf0 9 Old Lace 253,245,230 fdf5e6 10 Linen 240,240,230 faf0e6 11 Antique White 250,235,215 faebd7 12 Antique White 2 238,223,204 eedfcc 13 Antique White 3 205,192,176 cdc0b0 14 Antique White 4 139,131,120 8b8378 15 Papaya Whip 255,239,213 ffefd5 16 Blanched Almond 255,235,205 ffebcd 17 Bisque 255,228,196 ffe4c4 18 Bisque 2 238,213,183 eed5b7 19 Bisque 3 205,183,158 cdb79e 20 Bisque 4 139,125,107 8b7d6b 21 Peach Puff 255,218,185 ffdab9 22 Peach Puff 2 238,203,173 eecbad 23 Peach Puff 3 205,175,149 cdaf95 24 Peach Puff 4 139,119,101 8b7765 25 Navajo White 255,222,173 ffdead 26 Moccasin 255,228,181 ffe4b5 27 Corn silk 255,248,220 fff8dc 28 Corn silk 2 238,232,205 eee8dc 29 Cornsilk 3 205,200,177 cdc8b1 30 Corn silk 4 139,136,120 8b8878 31 Ivory 255,255,240 fffff0 32 Ivory 2 238,238,224 eeeee0 33 Ivory 3 205,205,193 cdcdc1 34 Ivory 4 139,139,131 8b8b83 35 Lemon Chiffon 255,250,205 fffacd 36 Seashell 255,245,238 fff5ee 37 Seashell 2 238,229,222 eee5de 38 Seashell 3 205,197,191 cdc5bf 39 Seashell 4 139,134,130 8b8682 40 Honeydew 240,255,240 f0fff0 41 Honeydew 2 244,238,224 e0eee0 42 Honeydew 3 193,205,193 c1cdc1 43 Honeydew 4 131,139,131 838b83 44 Mint Cream 245,255,250 f5fffa 45 Azure 240,255,255 f0ffff 46 Alice Blue 240,248,255 f0f8ff 47 Lavender 230,230,250 e6e6fa -

HP Indigo 12000 Digital Press a 29 Inch Digital Offset Press with Extensive Capabilities
HP Indigo 12000 Digital Press A 29 inch digital offset press with extensive capabilities Big ideas come to life The 29 inch HP Indigo 12000 Digital Press produces the widest commercial application range with superior print quality, high productivity, and wide versatility. Built on the best-selling and proven HP Indigo 10000 Digital Press, the press brings breakthrough printing capabilities that extend unique, high-value opportunities to grow business. Any commercial job An easy fit for offset printers, the HP Indigo 12000 Digital Press offers a solution for the digital printing of any commercial application on any substrate. Use the full sheet to print canvas wall art, high-impact posters, folders, oversized books, specialty products, and more. The leader in print quality and color Enabled by HP Indigo’s liquid ElectroInk technology and unique digi tal offset process, HP Indigo digital prints are the highest quality. Using dozens of software and hardware innovations, the press delivers the smoothest and sharpest prints in the industry, matching or even exceeding offset quality. HP Indigo ElectroInk has the widest digital color gamut, reaching up to 97% of PANTONE® colors and using up to 7 ink stations on press. A 5th ink station is standard. Breakthrough color matching tools ensure perfect color accuracy and consistency. Even higher productivity Printing 29 inch sheets in color at up to 4600 per hour, the press is capable of producing over two million color sheets per month. Print monochrome in duplex at 4600 sheets per hour. Sophisticated automation tools boost production efficiency and uptime. Widest media range Boost your sustainability One Shot extends substrates to canvas, synthetics and metalized media. -

Air Quality Assessment
A96 Dualling East of Huntly to Aberdeen A96 Online Dualling at Inverurie Supplementary Study Appendix B Air Quality Assessment Page B1 A96 Dualling East of Huntly to Aberdeen A96 Online Dualling at Inverurie Supplementary Study The following tables present the results of the Air Quality assessment of online dualling at Inverurie for all end-to-end route combinations, as different route option connections give rise to different levels of traffic. Results are shown for online dualling at Inverurie linking to the portion of the Orange route option from Drimmies to Pitcaple with further connections onto each of the Brown or Pink and Cyan or Red route options, giving four end-to-end combinations in total. Traffic modelling was used to predict flows on the existing A96 at Inverurie without any dualling online or offline (referred to as DM in the tables below - Do-Minimum) and for online dualling at Inverurie (referred to as DS in the tables below – Do-Something). The change from no A96 dualling (DM) to each end-to-end dualling combination incorporating online dualling at Inverurie was calculated to determine an assessment of the impact. Given traffic flows change at Blackhall Road as vehicles enter or leave the A96, results are provided for the road sections each side of Blackhall Road – Drimmies to Blackhall Road and Blackhall Road to Port Elphinstone. Results are provided for the D2APc (GSJ) and D2APb (At-Grade) layouts for predicted traffic flows in 2030 (the assumed year of opening) and 2045 (15 years after opening). There is no significant difference in traffic flows for the D2UAP (GSJ) and D2UAP (At- Grade) carriageway cross-section. -

RGB to Color Name Reference
RGB to Color Name Reference grey54 138;138;138 8A8A8A DodgerBlue1 30;144;255 1E90FF blue1 0;0;255 0000FF 00f New Tan 235;199;158 EBC79E Copyright © 1996-2008 by Kevin J. Walsh grey55 140;140;140 8C8C8C DodgerBlue2 28;134;238 1C86EE blue2 0;0;238 0000EE 00e Semi-Sweet Chocolate 107;66;38 6B4226 http://web.njit.edu/~walsh grey56 143;143;143 8F8F8F DodgerBlue3 24;116;205 1874CD blue3 0;0;205 0000CD Sienna 142;107;35 8E6B23 grey57 145;145;145 919191 DodgerBlue4 16;78;139 104E8B blue4 0;0;139 00008B Tan 219;147;112 DB9370 Shades of Black and Grey grey58 148;148;148 949494 170;187;204 AABBCC abc aqua 0;255;255 00FFFF 0ff Very Dark Brown 92;64;51 5C4033 Color Name RGB Dec RGB Hex CSS Swatch grey59 150;150;150 969696 LightBlue 173;216;230 ADD8E6 cyan 0;255;255 00FFFF 0ff Shades of Green Grey 84;84;84 545454 grey60 153;153;153 999999 999 LightBlue1 191;239;255 BFEFFF cyan1 0;255;255 00FFFF 0ff Dark Green 47;79;47 2F4F2F Grey, Silver 192;192;192 C0C0C0 grey61 156;156;156 9C9C9C LightBlue2 178;223;238 B2DFEE cyan2 0;238;238 00EEEE 0ee DarkGreen 0;100;0 006400 grey 190;190;190 BEBEBE grey62 158;158;158 9E9E9E LightBlue3 154;192;205 9AC0CD cyan3 0;205;205 00CDCD dark green copper 74;118;110 4A766E LightGray 211;211;211 D3D3D3 grey63 161;161;161 A1A1A1 LightBlue4 104;131;139 68838B cyan4 0;139;139 008B8B DarkKhaki 189;183;107 BDB76B LightSlateGrey 119;136;153 778899 789 grey64 163;163;163 A3A3A3 LightCyan 224;255;255 E0FFFF navy 0;0;128 000080 DarkOliveGreen 85;107;47 556B2F SlateGray 112;128;144 708090 grey65 166;166;166 A6A6A6 LightCyan1 224;255;255 -

Color Names Defined by SAS/GRAPH
Appendix C: Color Names Defined by SAS/GRAPH Introduction .............................................................................................. 219 Basic Hues ................................................................................................ 220 Blacks ....................................................................................................... 220 Blues ......................................................................................................... 221 Browns ...................................................................................................... 222 Grays ......................................................................................................... 223 Greens ...................................................................................................... 224 Olives ........................................................................................................ 226 Oranges ..................................................................................................... 226 Pinks ......................................................................................................... 227 Purples ...................................................................................................... 228 Reds .......................................................................................................... 229 Violets ....................................................................................................... 229 Whites ...................................................................................................... -

Magenta-Cyan Anaglyphs
Magenta-Cyan Anaglyphs Robin Lobel, January 2009 Fig 1. Magenta-Cyan glasses Abstract This paper present an alternative to usual anaglyph colors, by taking advantage of the low- frequency perception of blue. 1. Introduction and related works Anaglyph images were invented in 1853 [1] and so far it has not much evolved: by using glasses with a combination of two non-overlapping colors, it filters two separate pictures from one. Historically, the most popular color pairs are red/green and red/cyan. The advantage of red/cyan over red/green is a better color reproduction: cyan is a mix of two primary colors (green and blue), thus combined with red all colors are reconstructed. Other color pairs were tested, like yellow/blue (used in ColorCode 3D) [2] and green/magenta (used in Trioscopics 3D) [3]. The main problem with anaglyphs is retinal rivalry: separate colors are sent to each eyes, which can cause problems for long time viewing, and when reproducing color saturated objects. 2. The idea behind magenta-cyan anaglyphs To reduce retinal rivalry, more chromatic information must be sent to each eye. With current anaglyphs (red-cyan, green-magenta, yellow-blue) one eye receive one primary color, while the second receive two primary colors. Filters don't overlap to avoid ghosting, and allow good separation of the stereoscopic pair. However, we can take advantage of the low-frequency perception of blue by the human eye to send two primary colors per eye: if we blur blue channel only, it cause very few changes in the picture sharpness. Fig 2. -

SAS/GRAPH Color List
SAS Color Name RGB Value HLS Value Color description 1 BLACK CX000000 H0000000 Black WHITE CXFFFFFF H000FF00 White RED CXFF0000 H07880FF Red GREEN CX00FF00 H0F080FF Green BLUE CX0000FF H00080FF Blue PURPLE CX703070 H03C5066 Purple VIOLET CXB090D0 H01EB067 Violet ORANGE CXFF8000 H09680FF Orange YELLOW CXFFFF00 H0B480FF Yellow PINK CXFF0080 H05980FF Pink CYAN CX00FFFF H12C80FF Cyan MAGENTA CXFF00FF H03C80FF Magenta BROWN CXA05000 H09650FF Brown GOLD CXFFAA00 H0A080FF Gold LIME CXC0FF81 H0D2C0FF Lime GRAY CX808080 H0008000 Gray SAS Color Name RGB Value HLS Value Color description 2 LILAC CXE06090 H062A0AC Lilac MAROON CX700000 H07838FF Maroon SALMON CXFF0055 H06480FF Salmon TAN CXE0A860 H09AA0AC Tan ROSE CXFF6060 H078B0FF Rose CREAM CXE8D898 H0A8C0A2 Cream VIPK CXCC1B3B H06D74C3 Vivid pink STPK CXD9576E H06D98A1 Strong pink DEPK CX99293D H06D6194 Deep pink LIPK CXE599A7 H06DBF99 Light pink MOPK CXBA7C87 H06D9B4F Moderate pink DAPK CX995C67 H06D7A40 Dark pink PAPK CXE5BFC6 H06DD26D Pale pink GRPK CXBA9BA1 H06DAB2F Grayish pink PKWH CXEDDDE0 H06DE54E Pinkish white PKGR CXBFB2B5 H06DB917 Pinkish gray SAS Color Name RGB Value HLS Value Color description 3 VIR CX33070F H06D1DC3 Vivid red STR CX731727 H06D45AA Strong red DER CX4C1923 H06D3380 Deep red VDER CX190A0D H06D126D Very deep red MOR CX732E3A H06D506D Moderate red DAR CX40262B H06D3340 Dark red VDAR CX191213 H06D162D Very dark red LIGRR CX997078 H06D852A Light grayish red GRR CX73545A H06D6327 Grayish red DAGRR CX453C3D H06D4012 Dark grayish red BLR CX191717 H06D180D Blackish red RGR CX8C8385 -

Colorstyle — Choices for Color
Title stata.com colorstyle — Choices for color Syntax Description Remarks and examples Also see Syntax colorstyle Description black gs0 gray scale: 0 = black gs1 gray scale: very dark gray gs2 . gs15 gray scale: very light gray gs16 gray scale: 16 = white white blue bluishgray brown cranberry cyan dimgray between gs14 and gs15 dkgreen dark green dknavy dark navy blue dkorange dark orange eggshell emerald forest green gold gray equivalent to gs8 green khaki lavender lime ltblue light blue ltbluishgray light blue-gray, used by scheme s2color ltkhaki light khaki magenta maroon midblue midgreen mint navy 1 2 colorstyle — Choices for color olive olive teal orange orange red pink purple red sand sandb bright sand sienna stone teal yellow colors used by The Economist magazine: ebg background color ebblue bright blue edkblue dark blue eltblue light blue eltgreen light green emidblue midblue erose rose none no color; invisible; draws nothing background or bg same color as background foreground or fg same color as foreground ### RGB value; white = "255 255 255" #### CMYK value; yellow = "0 0 255 0" hsv # # # HSV value; white = "hsv 255 255 255" color*# color with adjusted intensity *# default color with adjusted intensity When specifying RGB, CMYK, or HSV values, it is best to enclose the values in quotes; type "128 128 128" and not 128 128 128. For a color palette showing an individual color, type palette color colorstyle , scheme(schemename) and for a palette comparing two colors, type palette color colorstyle colorstyle , scheme(schemename) For instance, you might type . palette color red green See[ G-2] palette. -

Photochromic Plastisol Inks - Cyan & Brown
Chameleon Photochromic Plastisol Inks - Cyan & Brown Revision: 17 Jul 2020 SAFETY DATA SHEET SECTION 1: Identification of the substance/mixture and of the company/undertaking 1.1 Product identifier - Product Name: Chameleon Photochromic Plastisol Inks - Cyan & Brown 1.2 Relevant identified uses of the substance or mixture and uses advised against - Use of the substance/mixture: Photochromic Dye in PVC Plastisol. Colourless until exposed to UV light. Developes one of the following colours depending on type: Brown or Cyan. 1.3 Details of the supplier of the safety data sheet - Name of Supplier: LCR Hallcrest - Address of Manufacturer: Riverside Buildings, Dock Road, Connah's Quay, Deeside, Flintshire, CH5 4DS, Wales. U.K. - Telephone: +44 (0) 1244 817107 - Email: [email protected] 1.4 Emergency telephone number - Emergency Telephone: +44 (0) 1244 818348 SECTION 2: Hazards identification 2.1 Classification of the substance or mixture - CLP: Skin Sens. 1, Aquatic Chronic 3 2.2 Label elements - Signal Word: Warning - Hazard statements May cause an allergic skin reaction. Harmful to aquatic life with long lasting effects. - Precautionary statements Wear protective gloves/protective clothing/eye protection/face protection. If skin irritation or rash occurs: Get medical advice/attention. Avoid release to the environment. 2.3 Other hazards - Contains: Methyl 1,2,2,6,6-pentamethyl-4-piperidyl sebacate Datasheet Number: plasphoto1 - v1.1.1 1 Prometheus version 1.6.1.2 SAFETY DATA SHEET - Chameleon Photochromic Plastisol Inks - Cyan & Brown Revision: 17 Jul 2020 SECTION 3: Composition/information on ingredients 3.2 Mixtures - Methyl 1,2,2,6,6-pentamethyl-4-piperidyl sebacate CAS Number: 82919-37-7 EC Number: 280-060-4 Concentration: 0 - 2.5% Categories: Skin Sens.