Chapter 7 ADDITIVE COLOR MIXING
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Impact of Properties of Thermochromic Pigments on Knitted Fabrics
International Journal of Scientific & Engineering Research, Volume 7, Issue 4, April-2016 1693 ISSN 2229-5518 Impact of Properties of Thermochromic Pigments on Knitted Fabrics 1Dr. Jassim M. Abdulkarim, 2Alaa K. Khsara, 3Hanin N. Al-Kalany, 4Reham A. Alresly Abstract—Thermal dye is one of the important indicators when temperature is changed. It is used in medical, domestic and electronic applications. It indicates the change in chemical and thermal properties. In this work it is used to indicate the change in human body temperature where the change in temperature between (30 – 41 oC) is studied .The change in color begin to be clear at (30 oC). From this study it is clear that heat flux increased (81%) between printed and non-printed clothes which is due to the increase in heat transfer between body and the printed cloth. The temperature has been increased to the maximum level that the human body can reach and a gradual change in color is observed which allow the use of this dye on baby clothes to indicate the change in baby body temperature and monitoring his medical situation. An additional experiment has been made to explore the change in physical properties to the used clothe after the printing process such as air permeability which shows a clear reduction in this property on printed region comparing with the unprinted region, the reduction can reach (70%) in this property and in some type of printing the reduction can reach (100%) which give non permeable surface. Dye fitness can also be increased by using binders and thickeners and the reduction in dyes on the surface of cloth is reached (15%) after (100) washing cycle. -

Color Theory for Painting Video: Color Perception
Color Theory For Painting Video: Color Perception • http://www.ted.com/talks/lang/eng/beau_lotto_optical_illusions_show_how_we_see.html • Experiment • http://www.youtube.com/watch?v=y8U0YPHxiFQ Intro to color theory • http://www.youtube.com/watch?v=059-0wrJpAU&feature=relmfu Color Theory Principles • The Color Wheel • Color context • Color Schemes • Color Applications and Effects The Color Wheel The Color Wheel • A circular diagram displaying the spectrum of visible colors. The Color Wheel: Primary Colors • Primary Colors: Red, yellow and blue • In traditional color theory, primary colors can not be mixed or formed by any combination of other colors. • All other colors are derived from these 3 hues. The Color Wheel: Secondary Colors • Secondary Colors: Green, orange and purple • These are the colors formed by mixing the primary colors. The Color Wheel: Tertiary Colors • Tertiary Colors: Yellow- orange, red-orange, red-purple, blue-purple, blue-green & yellow-green • • These are the colors formed by mixing a primary and a secondary color. • Often have a two-word name, such as blue-green, red-violet, and yellow-orange. Color Context • How color behaves in relation to other colors and shapes is a complex area of color theory. Compare the contrast effects of different color backgrounds for the same red square. Color Context • Does your impression od the center square change based on the surround? Color Context Additive colors • Additive: Mixing colored Light Subtractive Colors • Subtractive Colors: Mixing colored pigments Color Schemes Color Schemes • Formulas for creating visual unity [often called color harmony] using colors on the color wheel Basic Schemes • Analogous • Complementary • Triadic • Split complement Analogous Color formula used to create color harmony through the selection of three related colors which are next to one another on the color wheel. -
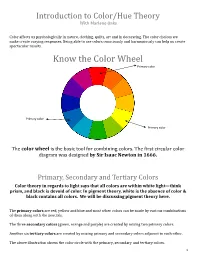
Know the Color Wheel Primary Color
Introduction to Color/Hue Theory With Marlene Oaks Color affects us psychologically in nature, clothing, quilts, art and in decorating. The color choices we make create varying responses. Being able to use colors consciously and harmoniously can help us create spectacular results. Know the Color Wheel Primary color Primary color Primary color The color wheel is the basic tool for combining colors. The first circular color diagram was designed by Sir Isaac Newton in 1666. Primary, Secondary and Tertiary Colors Color theory in regards to light says that all colors are within white light—think prism, and black is devoid of color. In pigment theory, white is the absence of color & black contains all colors. We will be discussing pigment theory here. The primary colors are red, yellow and blue and most other colors can be made by various combinations of them along with the neutrals. The three secondary colors (green, orange and purple) are created by mixing two primary colors. Another six tertiary colors are created by mixing primary and secondary colors adjacent to each other. The above illustration shows the color circle with the primary, secondary and tertiary colors. 1 Warm and cool colors The color circle can be divided into warm and cool colors. Warm colors are energizing and appear to come forward. Cool colors give an impression of calm, and appear to recede. White, black and gray are considered to be neutral. Tints - adding white to a pure hue: Terms about Shades - adding black to a pure hue: hue also known as color Tones - adding gray to a pure hue: Test for color blindness NOTE: Color theory is vast. -

PANTONE® Colorwebtm 1.0 COLORWEB USER MANUAL
User Manual PANTONE® ColorWebTM 1.0 COLORWEB USER MANUAL Copyright Pantone, Inc., 1996. All rights reserved. PANTONE® Computer Video simulations used in this product may not match PANTONE®-identified solid color standards. Use current PANTONE Color Reference Manuals for accurate color. All trademarks noted herein are either the property of Pantone, Inc. or their respective companies. PANTONE® ColorWeb™, ColorWeb™, PANTONE Internet Color System™, PANTONE® ColorDrive®, PANTONE Hexachrome™† and Hexachrome™ are trademarks of Pantone, Inc. Macintosh, Power Macintosh, System 7.xx, Macintosh Drag and Drop, Apple ColorSync and Apple Script are registered trademarks of Apple® Computer, Inc. Adobe Photoshop™ and PageMill™ are trademarks of Adobe Systems Incorporated. Claris Home Page is a trademark of Claris Corporation. Netscape Navigator™ Gold is a trademark of Netscape Communications Corporation. HoTMetaL™ is a trademark of SoftQuad Inc. All other products are trademarks or registered trademarks of their respective owners. † Six-color Process System Patent Pending - Pantone, Inc.. PANTONE ColorWeb Team: Mark Astmann, Al DiBernardo, Ithran Einhorn, Andrew Hatkoff, Richard Herbert, Rosemary Morretta, Stuart Naftel, Diane O’Brien, Ben Sanders, Linda Schulte, Ira Simon and Annmarie Williams. 1 COLORWEB™ USER MANUAL WELCOME Thank you for purchasing PANTONE® ColorWeb™. ColorWeb™ contains all of the resources nec- essary to ensure accurate, cross-platform, non-dithered and non-substituting colors when used in the creation of Web pages. ColorWeb works with any Web authoring program and makes it easy to choose colors for use within the design of Web pages. By using colors from the PANTONE Internet Color System™ (PICS) color palette, Web authors can be sure their page designs have rich, crisp, solid colors, no matter which computer platform these pages are created on or viewed. -

HP Indigo 7K Digital Press Press Digital 7K Indigo HP The
Add premium HP Indigo printing and watch your business grow. business your watch and printing Indigo HP premium Add ONE PRESS, ENDLESS OPPORTUNITIES. ENDLESS PRESS, ONE truly robust press. robust truly volumes day in, day out with this this with out day in, day volumes offset-matching quality and high high and quality offset-matching automated tools while printing printing while tools automated Simplify production with smart, smart, with production Simplify and over 20 specialty inks. inks. specialty 20 over and the widest range of media media of range widest the and customer satisfaction—with satisfaction—with customer and enables endless applications— endless enables The HP Indigo 7K Digital Press Press Digital 7K Indigo HP The HP Indigo 7K Digital Press Technical specifications Printing speed 120 four-color 8.5 x 11 (A4) pages per minute - two-up 160 color 8.5 x 11 (A4) pages per minute in EPM - two-up 240 two-color or monochrome 8.5 x 11 (A4) pages per minute - two-up Image resolution 812 dpi at 8 bit; addressability: 2438 x 2438 dpi HDI (High Definition Imaging) Line screens 144, 160, 175, 180, 180m, 210, HMF200 lpi Sheet size 13 x 19 in (330 x 482 mm) maximum Image size 12.48 x 18.26 in (317 x 464 mm) maximum Paper weight and thickness* Coated: 55 lb text to 130 lb cover (80 to 350 gsm); Uncoated: 40 lb text to 130 lb cover (60 to 350 gsm); Thickness 3 to 16 pt. (70 to 400 microns) Feeder Four drawers: Three drawers with 6 in (150 mm) each, 1500 sheets of 80 lb text (120 gsm) each One special jobs drawer: 2.5 in (70mm), 700 sheets of 80 lb text, (700 sheets of 120 gsm) A total of 5200 sheets of 80 lb text (120 gsm). -

Dance and the Imagination an Inspiration Turned Into a Fantasy
Twelve Conceptions of Imagination – by Leslie Stevenson (1) The ability to think of something not presently perceived, but spatio‐ temporally real. (2) The ability to think of whatever one acknowledges as possible in the spatio‐temporal world. (3) The ability to think of something that the subject believes to be real, but which is not. (4) The ability to think of things that one conceives of as fictional. (5) The ability to entertain mental images. (6) The ability to think of anything at all. (7) The non‐rational operations of the mind, that is, those explicable in terms of causes rather than reasons. (8) The ability to form perceptual beliefs about public objects in space and time. (9) The ability to sensuously appreciate works of art or objects of natural beauty without classifying them under concepts or thinking of them as useful. (10) The ability to create works of art that encourage such sensuous appreciation. (11) The ability to appreciate things that are expressive or revelatory of the meaning of human life. (12) The ability to create works of art that express something deep about the meaning of life. Dance and the Imagination An inspiration turned into a fantasy based reality A dream envisioned and resourcefully staged Mental creative pictures coming to life Inventiveness using human movement in space Innovation and individuality whether improvised or more formally choreographed Expressive bodily ideas Experiential corporal representations Artistic power and ingenuity transposed into physical form Presentational musculo-skeletal -

Pale Intrusions Into Blue: the Development of a Color Hannah Rose Mendoza
Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2004 Pale Intrusions into Blue: The Development of a Color Hannah Rose Mendoza Follow this and additional works at the FSU Digital Library. For more information, please contact [email protected] THE FLORIDA STATE UNIVERSITY SCHOOL OF VISUAL ARTS AND DANCE PALE INTRUSIONS INTO BLUE: THE DEVELOPMENT OF A COLOR By HANNAH ROSE MENDOZA A Thesis submitted to the Department of Interior Design in partial fulfillment of the requirements for the degree of Master of Fine Arts Degree Awarded: Fall Semester, 2004 The members of the Committee approve the thesis of Hannah Rose Mendoza defended on October 21, 2004. _________________________ Lisa Waxman Professor Directing Thesis _________________________ Peter Munton Committee Member _________________________ Ricardo Navarro Committee Member Approved: ______________________________________ Eric Wiedegreen, Chair, Department of Interior Design ______________________________________ Sally Mcrorie, Dean, School of Visual Arts & Dance The Office of Graduate Studies has verified and approved the above named committee members. ii To Pepe, te amo y gracias. iii ACKNOWLEDGMENTS I want to express my gratitude to Lisa Waxman for her unflagging enthusiasm and sharp attention to detail. I also wish to thank the other members of my committee, Peter Munton and Rick Navarro for taking the time to read my thesis and offer a very helpful critique. I want to acknowledge the support received from my Mom and Dad, whose faith in me helped me get through this. Finally, I want to thank my son Jack, who despite being born as my thesis was nearing completion, saw fit to spit up on the manuscript only once. -

Several Color Appearance Phenomena in Color Reproduction
2nd International Conference on Electronic & Mechanical Engineering and Information Technology (EMEIT-2012) Several Color Appearance Phenomena in Color Reproduction Qin-ling Dai1,a, Xiao-zhou Li2*,b, Ai Xu2 1 School of Materials Engineering (Southwest Forestry University), Kunming, China 650224 2 Key Laboratory of Pulp & Paper Science and Technology (Shandong Polytechnic University), Ministry of Education, Ji’nan, China, 250353 [email protected], bcorresponding author: [email protected] Keywords: color reproduction, color appearance, color appearance phenomena Abstract. Color perceived performance was influenced by various color appearance phenomena caused by varying viewing conditions in color reproduction process. It is necessary to do some research on the color appearance phenomena to represent the color appearance models qualitatively and quantitatively and accurate color reproduction easily. Only the phenomena were studied thoroughly, could the color transmission and reproduction be well performed. The color appearance and common color appearance phenomena of color reproduction were analyzed in this paper. And the basic theory of color appearance in color reproduction was also studied. Introduction High fidelity digital printing plays an important role in high fidelity color transmission and reproduction and it is one of the most important techniques to perform high fidelity color reproduction. High fidelity digital printing helps to perform accurate color reproduction of the original which can’t be performed because of paper and ink in traditional printing process [1]. In color printing, the color difference caused by paper, ink and viewing conditions is various. The difference is not only colorimetric difference but also different color appearance phenomena. While the different color appearance phenomenon is the leading factor to influence the color vision perceived. -

Color Gamut of Halftone Reproduction*
Color Gamut of Halftone Reproduction* Stefan Gustavson†‡ Department of Electrical Engineering, Linkøping University, S-581 83 Linkøping, Sweden Abstract tern then gets attenuated once more by the pattern of ink that resides on the surface, and the finally reflected light Color mixing by a halftoning process, as used for color is the result of these three effects combined: transmis- reproduction in graphic arts and most forms of digital sion through the ink film, diffused reflection from the hardcopy, is neither additive nor subtractive. Halftone substrate, and transmission through the ink film again. color reproduction with a given set of primary colors is The left-hand side of Fig. 2 shows an exploded view of heavily influenced not only by the colorimetric proper- the ink layer and the substrate, with the diffused reflected ties of the full-tone primaries, but also by effects such pattern shown on the substrate. The final viewed image as optical and physical dot gain and the halftone geom- is a view from the top of these two layers, as shown to etry. We demonstrate that such effects not only distort the right in Fig. 2. The dots do not really increase in the transfer characteristics of the process, but also have size, but they have a shadow around the edge that makes an impact on the size of the color gamut. In particular, a them appear larger, and the image is darker than what large dot gain, which is commonly regarded as an un- would have been the case without optical dot gain. wanted distortion, expands the color gamut quite con- siderably. -

Color Combinations and Contrasts
COLOR COMBINATIONS AND CONTRASTS Full Value Color Combinations Above are 18 color combinations tested for visibility, using primary and secondary colors, of full hue and value. Visibility is ranked in the sequence shown, with 1 being the most visible and 18 being the least visible. Readability It is essential that outdoor designs are easy to read. Choose colors with high contrast in both hue and value. Contrasting colors are viewed well from great distances, while colors with low contrast will blend together and obscure a message. In fact, research demonstrates that high color contrast can improve outdoor advertising recall by 38 percent. A standard color wheel clearly illustrates the importance of contrast, hue and value. Opposite colors on the wheel are complementary. An example is red and green (as shown above). They respresent a good contrast in hue, but their values are similar. It is difficult for the human eye to process the wavelength variations associated with complementary colors. Therefore, a quivering or optical distortion is sometimes detected when two complemen- tary colors are used in tandem. Adjacent colors, such as blue and green, make especially poor combinations since their contrast is similar in both hue and value. As a result, adjacent colors create contrast that is hard to discern. Alternating colors, such as blue and yellow, produce the best combinations since they have good contrast in both hue and value. Black contrasts well with any color of light value and white is a good contrast with colors of dark value. For example, yellow and black are dissimilar in the contrast of both hue and value. -

Color Mixing Ratios
Colour Mixing: Ratios Color Theory with Tracy Moreau Learn more at DecoArt’s Art For Everyone Learning Center www.tracymoreau.net Primary Colours In painting, the three primary colours are yellow, red, and blue. These colors cannot be created by mixing other colours. They are called primary because all other colours are derived from them. Mixing Primary Colours Creates Secondary Colours If you combine two primary colours you get a secondary colour. For example, red and blue make violet, yellow and red make orange, and blue and yellow make green. If you mix all of the primary colours together you get black. The Mixing Ratio for Primary Colours To get orange, you mix the primary colours red and yellow. The mixing ratio of these two colours determines which shade of orange you will get after mixing. For example, if you use more red than yellow you will get a reddish-orange. If you add more yellow than red you will get a yellowish-orange. Experiment with the shades you have to see what you can create. Try out different combinations and mixing ratios and keep a written record of your results so that you can mix the colours again for future paintings. www.tracymoreau.net Tertiary Colours By mixing a primary and a secondary colour or two secondary colours you get a tertiary colour. Tertiary colours such as blue-lilac, yellow-green, green-blue, orange-yellow, red-orange, and violet-red are all created by combining a primary and a secondary colour. The Mixing Ratios of Light and Dark Colours If you want to darken a colour, you only need to add a small amount of black or another dark colour. -

Adobe Photoshop 7.0 Design Professional
Adobe Photoshop CS Design Professional INCORPORATING COLOR TECHNIQUES Chapter Lessons Work with color to transform an image User the Color Picker and the Swatches palette Place a border around an image Blend colors using the Gradient Tool Add color to a grayscale image Use filters, opacity, and blending modes Match colors Incorporating Color Techniques Chapter D 2 Incorporating Color Techniques Using Color Develop an understanding of color theory and color terminology Identify how Photoshop measures, displays and prints color Learn which colors can be reproduced well and which ones cannot Incorporating Color Techniques Chapter D 3 Color Modes Photoshop displays and prints images using specific color modes Color mode or image mode determines how colors combine based on the number of channels in a color model Different color modes result in different levels of color detail and file size – CMYK color mode used for images in a full-color print brochure – RGB color mode used for images in web or e-mail to reduce file size while maintaining color integrity Incorporating Color Techniques Chapter D 4 Color Modes L*a*b Model – Based on human perception of color – Numeric values describe all colors seen by a person with normal vision Grayscale Model – Grayscale mode uses different shades of gray RGB (Red Green Blue) Mode used for online images – Assign intensity value to each pixel – Intensity values range from 0 (black) to 255 (white) for each of the RGB (red, green, blue) components in a color image • Bright red color has an R value of 246, a G value of 20, and a B value of 50.