DOCSLIB.ORG

COMPUTER SIMULATION STUDIES of ... -.:University of Limpopo

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
COMPUTER SIMULATION STUDIES of ... -.:University of Limpopo COMPUTER SIMULATION STUDIES OF SPINEL LiMn2O4 AND SPINEL LiNiXMn2-XO4 (0≤x≤2) By KEMERIDGE TUMELO MALALTJI Thesis Submitted in fulfilment of the requirements for the degree of Doctor of Philosophy In Physics in the FACULTY OF SCIENCES AND AGRICULTURE (School of Physical and Mineral Sciences) at the UNIVERSITY OF LIMPOPO SUPERVISOR: Prof. R.R. Maphanga CO- SUPERVISORS: Prof. P.E. Ngoepe (Dated: 29 October 2019) Declaration I, Kemeridge Tumelo Malatji confirm that the work presented in this thesis is my own. Where information has been derived from other sources, I confirm that this has been indicated in the thesis. I agree that the Library may lend or copy this dissertation on request. Signature: Date: 29/10/2019 Name: Mr K.T. Malatji ii Abstract LiMn2O4 spinel (LMO) is a promising cathode material for secondary lithium-ion batteries which, despite its high average voltage of lithium intercalation, suffers crystal symmetry lowering due to the Jahn-Teller active six-fold Mn3+ cations. Although Ni has been proposed as a suitable substitutional dopant to improve the energy density of LiMn2O4 and enhance the average lithium intercalation voltage, the thermodynamics of Ni incorporation and its effect on the electrochemical properties of this spinel are not fully understood. Firstly, structural, electronic and mechanical properties of spinel LiMn2O4 and LiNixMn2-xO4 have been calculated out using density functional theory employing the pseudo-potential plane-wave approach within the generalised gradient approximation, together with Virtual Cluster Approximation. The structural properties included equilibrium lattice parameters; electronic properties cover both total and partial density of states and mechanical properties investigated elastic properties of all systems. Secondly, the pressure variation of several properties was investigated, from 0 GPa to 50 GPa. Nickel concentration was changed and the systems LiNi0.25Mn1.75O4, LiNi0.5Mn1.5O4 LiNi0.75Mn1.25O4 and LiNi0.875Mn1.125O4 were studied. Calculated lattice parameters for LiMn2O4 and LiNi0.5Mn1.5O4 systems are consistent with the available experimental and literature results. The average Mn(Ni)-O bond length for all systems was found to be 1.9 Å. The bond lengths decreased with an increase in nickel content, except for LiNi0.75Mn1.25O4, which gave the same results as LiNi0.25Mn1.75O4. Generally, analysis of electronic properties predicted the nature of bonding for both pure and doped systems with partial density of states showing the contribution of each metal in our systems. All systems are shown to be metallic as it has been previously observed for pure spinel LiMn2O4, and mechanical properties, as deduced from elastic properties, depicted their stabilities. Furthermore, the cluster expansion formalism was used to investigate the nickel doped LiMn2O4 phase stabilities. The method determines stable multi-component crystal structures and ranks metastable structures by the enthalpy of formation while iii maintaining the predictive power and accuracy of first-principles density functional methods. The ground-state phase diagram with occupancy of Mn 0.81 and Ni 0.31 generated various structures with different concentrations and symmetries. The findings predict that all nickel doped LMO structures on the ground state line are most likely stable. Relevant structures (Li4Ni8O16, Li12MnNi17O48, Li4Mn6Ni2O16, Li4Mn7NiO16 and Li4Mn8O16) were selected on the basis of how well they weighed the cross-validation (CV) score of 1.1 meV, which is a statistical way of describing how good the cluster expansion is at predicting the energy of each stable structure. Although the structures have different symmetries and space groups they were further investigated by calculating the mechanical and vibrational properties, where the elastic constants and phonon vibrations indicated that the structures are stable in accordance with stability conditions of mechanical properties and phonon dispersions. Lastly, a computer program that identifies different site occupancy configurations for any structure with arbitrary supercell size, space group or composition was employed to investigate voltage profiles for LiNixMn2-xO4. The density functional theory calculations, with a Hubbard Hamiltonian (DFT+U), was used to study the thermodynamics of mixing for Li(Mn1-xNix)2O4 solid solution. The results suggested that LiMn1.5Ni0.5O4 is the most stable composition from room temperature up to at least 1000K, which is in excellent agreement with experiments. It was also found that the configurational entropy is much lower than the maximum entropy at 1000K, indicating that higher temperatures are required to reach a fully disordered solid solution. The maximum average lithium intercalation voltage of 4.8 eV was calculated for the LiMn1.5Ni0.5O4 composition which correlates very well with the experimental value. The temperature has a negligible effect on the Li intercalation voltage of the most stable composition. The approach presented here shows that moderate Ni doping of the LiMn2O4 leads to a substantial change in the average voltage of lithium intercalation, suggesting an attractive route for tuning the cathode properties of this spinel. iv ACKNOWLEDGEMENTS I would like to thank my supervisor Prof. R.R. Maphanga for all the unconditional encouragement, guidance, support, mentoring. Thanks for making the journey in the research field an interesting one. My gratitude also goes to my co-supervisor Prof. P.E. Ngoepe for this opportunity, contribution throughout this study and award of the project. I am forever humbled by what you saw in me and for your mentorship. Above all, I would like to thank the almighty God for all the strength, patience and perseverance He has installed in me during all the years of my studies, without Him this work wouldn’t have been started. I fully acknowledge the financial support from the National Research Foundation. This research wouldn’t have been a success if it was not of their financial backing and it encouraged my work ethic. Ample thanks to all the compatriots of the Material Modeling Center whose friendship, guidance and support had made the center more than an area to study at; “It is and will always be a jam to work with you fellas”. Finally, abundant thanks to my parents Mosadi Sophy Malatji and Johannes Anaph Malatji for their warm support, constant believe, encouragement and the love they showed me during this journey and life. They have contributed to me being the man I am today. My brothers (Kholofelo Brian Malatji and Tshegofatjo Anaph Malatji) thanks a lot your brotherhood, which reminded me that my efforts would make a difference in your lives. To my grandmothers (Shibe and Boreadi), aunts and uncle, your contribution will always be of paramount significance in my heart. To my beautiful partner your support from reading my work and pushing me to finish meant a lot. I would also like to give thanks to my many friends and extended family members who were always positively inquisitive about my progress. I wish to thank everybody with whom I have shared experiences in life. Most importantly, ample thanks to my late grandfather Samson Galiade Gozo ‘aka Gita’ for always making me believe on how important education is. Always full of laughter. v Dedication This work is dedicated to my lovely parents Johannes Anaph Malatji and Mosadi Sophy Malatji, my brothers (Kholofelo Brian Malatji and Tshegofatjo Anaph Malatji). To my late grandfather wherever you are, this is for you, may your soul rest in peace “Galiade”. “It’s better to die for an idea that will live than to live for an idea that will die” –Onkgopotse Abram Tiro vi Contents Declaration .............................................................................................................. ii Abstract .................................................................................................................. iii Dedication .............................................................................................................. vi List of Figures .......................................................................................................... x List of Tables ......................................................................................................... xv ............................................................................................................... xv Introduction ......................................................................................................... 1 General Introduction ..................................................................................... 1 Lithium-ion Batteries ..................................................................................... 2 Doping in LiMn2O4 ........................................................................................ 7 Structural Properties of LiMn2O4 ................................................................. 10 The rationale of the Study ........................................................................... 12 Outline of the Study .................................................................................... 14 .............................................................................................................. 15 Methodology ..................................................................................................... 15 Introduction ................................................................................................. 15 Density Functional Theory
Load more

Recommended publications
  • (12) United States Patent (10) Patent No.: US 7.449,161 B2 Boryta Et Al
    USOO74491.61B2 (12) United States Patent (10) Patent No.: US 7.449,161 B2 Boryta et al. (45) Date of Patent: Nov. 11, 2008 (54) PRODUCTION OF LITHIUM COMPOUNDS 4,207,297 A * 6/1980 Brown et al. ............. 423,179.5 DIRECTLY FROM LITHIUM CONTAINING 4,243,641 A * 1/1981 Ishimori et al. .......... 423/179.5 BRINES 4.261,960 A * 4/1981 Boryta ............. ... 423,179.5 4,271,131. A * 6/1981 Brown et al. ...... ... 423,179.5 4,274,834. A 6/1981 Brown et al. .............. 23,302 R (75) Inventors: Daniel Alfred Boryta, Cherryville, NC 4,463,209 A * 7/1984 Kursewicz et al. .......... 585/467 (US); Teresita Frianeza Kullberg, 4,465,659 A * 8/1984 Cambridge et al. ......... 423,495 Gastonia, NC (US); Anthony Michael 4,588,565 A * 5/1986 Schultze et al. .......... 423,179.5 Thurston, Edmond, OK (US) 4,747.917 A * 5/1988 Reynolds et al. ............ 205,512 4,859,343 A * 8/1989 Frianeza-Kullberg (73) Assignee: Chemetall Foote Corporation, Kings et al. .......................... 210,679 Mountain, NC (US) 4,980,136 A * 12/1990 Brown et al. ... 423,179.5 5,049,233 A 9, 1991 Davis .......................... 216.93 (*) Notice: Subject to any disclaimer, the term of this 5,219,550 A * 6/1993 Brown et al. ............. 423 (419.1 patent is extended or adjusted under 35 5,599,516 A * 2/1997 Bauman et al. .......... 423/179.5 U.S.C. 154(b) by 0 days. 5,939,038 A * 8/1999 Wilkomirsky ............... 423,276 5.993,759 A * 1 1/1999 Wilkomirsky ...........
    [Show full text]
  • The Secondary Phosphate Minerals from Conselheiro Pena Pegmatite District (Minas Gerais, Brazil): Substitutions of Triphylite and Montebrasite Scholz, R.; Chaves, M
    The secondary phosphate minerals from Conselheiro Pena Pegmatite District (Minas Gerais, Brazil): substitutions of triphylite and montebrasite Scholz, R.; Chaves, M. L. S. C.; Belotti, F. M.; Filho, M. Cândido; Filho, L. Autor(es): A. D. Menezes; Silveira, C. Publicado por: Imprensa da Universidade de Coimbra URL persistente: URI:http://hdl.handle.net/10316.2/31441 DOI: DOI:http://dx.doi.org/10.14195/978-989-26-0534-0_27 Accessed : 2-Oct-2021 20:21:49 A navegação consulta e descarregamento dos títulos inseridos nas Bibliotecas Digitais UC Digitalis, UC Pombalina e UC Impactum, pressupõem a aceitação plena e sem reservas dos Termos e Condições de Uso destas Bibliotecas Digitais, disponíveis em https://digitalis.uc.pt/pt-pt/termos. Conforme exposto nos referidos Termos e Condições de Uso, o descarregamento de títulos de acesso restrito requer uma licença válida de autorização devendo o utilizador aceder ao(s) documento(s) a partir de um endereço de IP da instituição detentora da supramencionada licença. Ao utilizador é apenas permitido o descarregamento para uso pessoal, pelo que o emprego do(s) título(s) descarregado(s) para outro fim, designadamente comercial, carece de autorização do respetivo autor ou editor da obra. Na medida em que todas as obras da UC Digitalis se encontram protegidas pelo Código do Direito de Autor e Direitos Conexos e demais legislação aplicável, toda a cópia, parcial ou total, deste documento, nos casos em que é legalmente admitida, deverá conter ou fazer-se acompanhar por este aviso. pombalina.uc.pt digitalis.uc.pt 9 789892 605111 Série Documentos A presente obra reúne um conjunto de contribuições apresentadas no I Congresso Imprensa da Universidade de Coimbra Internacional de Geociências na CPLP, que decorreu de 14 a 16 de maio de 2012 no Coimbra University Press Auditório da Reitoria da Universidade de Coimbra.
    [Show full text]
  • (12) Patent Application Publication (10) Pub. No.: US 2008/0233042 A1 Boryta Et Al
    US 20080233042A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2008/0233042 A1 Boryta et al. (43) Pub. Date: Sep. 25, 2008 (54) PRODUCTION OF LITHIUM COMPOUNDS 11/332,134, filed on Jan. 13, 2006, now Pat. No. 7,214, DIRECTLY FROM LITHIUM CONTAINING 355, which is a division of application No. 10/395,984, BRINES filed on Mar. 25, 2003, now Pat. No. 7,157,065, which is a continuation-in-part of application No. 09/707, (76) Inventors: Daniel Alfred Boryta, Cherryville, 427, filed on Nov. 7, 2000, now Pat. No. 6,936,229, NC (US); Teresita Frianeza which is a division of application No. 09/353,185, filed Kullberg, Gastonia, NC (US); on Jul. 14, 1999, now Pat. No. 6,207,126. Anthony Michael Thurston, Edmond, OK (US) Publication Classification Correspondence Address: (51) Int. C. FULBRIGHT & JAWORSKI, LLP C22B 26/10 (2006.01) 666 FIFTHAVE NEW YORK, NY 10103-3198 (US) (52) U.S. Cl. ..................................................... 423/499.3 (21) Appl. No.: 12/114,054 (57) ABSTRACT (22) Filed: May 2, 2008 Methods and apparatus for the production of low sodium lithium carbonate and lithium chloride from a brine concen Related U.S. Application Data trated to about 6.0 wt % lithium are disclosed. Methods and (60) Continuation of application No. 1 1/706027, filed on apparatus for direct recovery of technical grade lithium chlo Feb. 14, 2007, which is a division of application No. ride from the concentrated brine are also disclosed. Patent Application Publication Sep. 25, 2008 Sheet 1 of 7 US 2008/0233042 A1 LITHIUM CARBONATE PROCESSFLOW DIAGRAM (A) 2 CD SOLID SODAASH 4 3 Mg MUD \ SAS 6 FROM C5 5 REACTOR LIQUOR MOTHER LIOUOR WASH FILTER (10) BRINE + WASHFILTRATE 0.5 - 1.2% Li 2ND STAGE 12 REACTOR FILTER Li2CO3 REACTOR 18 FILTER MOTHER LIQUOR (19) WASH WATER FLTRATE PROCESS BLEED WET LITHIUM CARBONATE9 21 DRYER WET Li2CO3 22 TO B1 TECH GRADE Li2CO3 FIG.
    [Show full text]
  • Local Peralkalinity in Peraluminous Granitic Pegmatites. I. Evidence
    This is the peer-reviewed, final accepted version for American Mineralogist, published by the Mineralogical Society of America. The published version is subject to change. Cite as Authors (Year) Title. American Mineralogist, in press. DOI: https://doi.org/10.2138/am-2021-7790. http://www.minsocam.org/ Revision 1 1 Local peralkalinity in peraluminous granitic pegmatites. I. Evidence 2 from whewellite and hydrogen carbonate in fluid inclusions 3 YONGCHAO LIU1,2, CHRISTIAN SCHMIDT2,*, AND JIANKANG LI1 4 1MNR Key Laboratory of Metallogeny and Mineral Assessment, Institute of Mineral Resources, 5 Chinese Academy of Geological Sciences, Beijing 100037, China 6 2GFZ German Research Centre for Geosciences, Telegrafenberg, 14473 Potsdam, Germany 7 *Corresponding author: [email protected] 8 9 ABSTRACT 10 Fluid inclusions in pegmatite minerals were studied using Raman spectroscopy to 11 determine the carbon species. Carbon dioxide is very abundant in the aqueous liquid and vapor − 12 phases. Occasionally, CH4 was found in the vapor. In the aqueous liquid, HCO3 was detected in 13 fluid inclusions in tantalite-(Mn) from the Morrua Mine and in late-stage quartz from the Muiâne 14 pegmatite and the Naipa Mine, all in the Alto Ligonha District, Mozambique. Moreover, we 15 observed a carbonate (calcite group) in fluid inclusions in garnet from the Naipa Mine and in 16 beryl from the Morrua Mine, both in the Alto Ligonha District, Mozambique, and a calcite-group 17 carbonate and whewellite [CaC2O4∙H2O] in fluid inclusions in topaz from Khoroshiv, Ukraine. 18 The occurrence of oxalate is interpreted to be due to a reaction of some form of carbon (possibly 19 CO or bitumen) with a peralkaline fluid.
    [Show full text]
  • The Journal of ^ Y Volume 26 No
    Gemmolog^^ The Journal of ^ y Volume 26 No. 8 October 1999 fj J The Gemmological Association and Gem Testing Laboratory of Great Britain Gemmological Association and Gem Testing Laboratory of Great Britain 27 Greville Street, London EC1N 8TN Tel: 020 7404 3334 Fax: 020 7404 8843 e-mail: [email protected] Website: www.gagtl.ac.uk/gagtl. President: Professor R.A. Howie Vice-Presidents: E.M. Bruton, A.E. Farn, D.G. Kent, R.K. Mitchell Honorary Fellows: Chen Zhonghui, R.A. Howie, R.T. Liddicoat Jnr, K. Nassau Honorary Life Members: H. Bank, D.J. Callaghan, E.A. Jobbins, H. Tillander Council of Management: T.J. Davidson, N.W. Deeks, R.R. Harding, I. Mercer, J. Monnickendam, M J. O'Donoghue, E. Stern, I. Thomson, V.P. Watson Members' Council: A.J. Allnutt, P. Dwyer-Hickey, S.A. Everitt, A.G. Good, J. Greatwood, B. Jackson, L. Music, J.B. Nelson, PG. Read, R. Shepherd, P.J. Wates, C.H. Winter Branch Chairmen: Midlands - G.M. Green, North West -1. Knight, Scottish - B. Jackson Examiners: A.J. Allnutt, MSc, Ph.D., FGA, L. Bartlett, B.Sc, MPhiL, FGA, DGA, E.M. Bruton, FGA, DGA, S. Coelho, B.Sc, FGA, DGA, Prof. A.T. Collins, B.Sc, Ph.D, A.G. Good, FGA, DGA, J. Greatwood, FGA, G.M. Howe, FGA, DGA, B. Jackson, FGA, DGA, G.H. Jones, B.Sc, Ph.D., FGA, M. Newton, B.Sc, D.Phil., C.J.E. Oldershaw, B.Sc (Hons), FGA, H.L. Plumb, B.Sc, FGA, DGA, R.D. Ross, B.Sc, FGA, DGA, PA.
    [Show full text]
  • Standard X-Ray Diffraction Powder Patterns NATIONAL BUREAU of STANDARDS
    NBS MONOGRAPH 25—SECTION 1 9 CO Q U.S. DEPARTMENT OF COMMERCE/National Bureau of Standards Standard X-ray Diffraction Powder Patterns NATIONAL BUREAU OF STANDARDS The National Bureau of Standards' was established by an act of Congress on March 3, 1901. The Bureau's overall goal is to strengthen and advance the Nation's science and technology and facilitate their effective application for public benefit. To this end, the Bureau conducts research and provides: (1) a basis for the Nation's physical measurement system, (2) scientific and technological services for industry and government, (3) a technical basis for equity in trade, and (4) technical services to promote public safety. The Bureau's technical work is per- formed by the National Measurement Laboratory, the National Engineering Laboratory, and the Institute for Computer Sciences and Technology. THE NATIONAL MEASUREMENT LABORATORY provides the national system of physical and chemical and materials measurement; coordinates the system with measurement systems of other nations and furnishes essentia! services leading to accurate and uniform physical and chemical measurement throughout the Nation's scientific community, industry, and commerce; conducts materials research leading to improved methods of measurement, standards, and data on the properties of materials needed by industry, commerce, educational institutions, and Government; provides advisory and research services to other Government agencies; develops, produces, and distributes Standard Reference Materials; and provides calibration
    [Show full text]
  • (12) United States Patent (10) Patent No.: US 8,722,004 B2 Wu Et Al
    USOO8722004B2 (12) United States Patent (10) Patent No.: US 8,722,004 B2 Wu et al. (45) Date of Patent: May 13, 2014 (54) METHOD FOR THE PREPARATION OFA 6,730,281 B2 * 5/2004 Barker et al. ................. 423.306 LITHIUM PHOSPHATE COMPOUND WITH 2006/0147365 A1* 7, 2006 Okada et al. ... ... 423.306 2006/0257307 A1* 11/2006 Yang ........... ... 423.306 AN OLIVINE CRYSTAL STRUCTURE 2008, 0008938 A1* 1/2008 Wu et al. ... 429,221 2010.0059.706 A1 3/2010 Dai et al. ................... 252, 1821 (75) Inventors: Mark Y. Wu, Wujie Township, Yilan County (TW); Cheng-Yu Hsieh, Wujie FOREIGN PATENT DOCUMENTS Township, Yilan County (TW); Chih-Hao Chiu, Wujie Township, Yilan TW I254.031 5, 2006 County (TW) TW I29263.5 1, 2008 (73) Assignee: Phosage, Inc., Yilan County (TW) OTHER PUBLICATIONS (*) Notice: Subject to any disclaimer, the term of this Shiraishi et al., “Formation of impurities on phospho-olivine patent is extended or adjusted under 35 LiFePO4 during hydrothermal synthesis,” Journal of Power Sources, U.S.C. 154(b) by 710 days. 2005, pp. 555-558, vol. 146. (21) Appl. No.: 12/478,387 * cited by examiner (22) Filed: Jun. 4, 2009 Primary Examiner — Melvin C Mayes (65) Prior Publication Data Assistant Examiner — Colette Nguyen US 2010/O2O2951A1 Aug. 12, 2010 (74) Attorney, Agent, or Firm — Muncy, Geissler, Olds & Lowe, P.C. (30) Foreign Application Priority Data (57) ABSTRACT Feb. 12, 2009 (TW) ............................... 98104490 A The present invention relates to a method for the preparation (51) Int. Cl. of a lithium phosphate compound with an olivine crystal COB 25/26 (2006.01) structure, which has a chemical formula of Li, M.M'PO, (52) U.S.
    [Show full text]
  • Technological Gaps Inhibiting the Exploitation of Crms Primary Resources
    SCRREEN Coordination and Support Action (CSA) This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 730227. Start date : 2016-11-01 Duration : 38 Months www.scrreen.eu Technological gaps inhibiting the exploitation of CRMs primary resources Authors : Dr. Jordi GUIMERA (AMPHOS21) SCRREEN - D6.1 - Issued on 2019-12-18 22:10:32 by AMPHOS21 SCRREEN - D6.1 - Issued on 2019-12-18 22:10:32 by AMPHOS21 SCRREEN - Contract Number: 730227 Project officer: Jonas Hedberg Document title Technological gaps inhibiting the exploitation of CRMs primary resources Author(s) Dr. Jordi GUIMERA Number of pages 126 Document type Deliverable Work Package WP6 Document number D6.1 Issued by AMPHOS21 Date of completion 2019-12-18 22:10:32 Dissemination level Public Summary Technological gaps inhibiting the exploitation of CRMs primary resources Approval Date By 2019-12-19 10:05:27 Mrs. Maria TAXIARCHOU (LabMet, NTUA) 2020-01-27 08:01:27 Mr. Stéphane BOURG (CEA) SCRREEN - D6.1 - Issued on 2019-12-18 22:10:32 by AMPHOS21 SCRREEN This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 730227. Start date: 2016-11-01 Duration: 37 Months DELIVERABLE 6.1: TECHNOLOGICAL GAPS AND BARRIERS ON PRIMARY RESOURCES AUTHOR(S): Aina Bruno Diaz (Amphos 21) Susanna Casanovas (Amphos 21) Lena Sundqvist (SWERIM) Stéphane Bourg (CEA) Michael Samouhos (NTUA) DATE OF SUBMISSION: 09/12/2019 CONTENT List of figures ..........................................................................................................................................................
    [Show full text]
  • ABSTRACT ALLEN, JOSHUA LEE. Molecular Interactions of The
    ABSTRACT ALLEN, JOSHUA LEE. Molecular Interactions of the Difluoro(oxalato)borate Anion and Its Application for Lithium Ion Battery Electrolytes. (Under the direction of Dr. Wesley A. Henderson). Understanding the molecular interactions within electrolyte mixtures is essential for designing next generation electrolyte materials for high-voltage lithium ion (Li-ion) battery applications. Despite significant advancements in Li-ion battery electrode materials, which have theoretically enabled cell operation in excess of 5 V (vs. Li/Li+), the state-of-the-art electrolyte formulation has remained largely unchanged over two decades after its initial commercialization. To optimize the electrolyte properties, it is crucial to understand and relate the molecular-level interactions to the measured bulk properties. In the present study, these interactions have been explored through the use of the following techniques: phase diagrams (DSC analysis), X-ray single crystal structural determination, spectroscopic vibrational analysis (Raman) of the solvent and anion bands, and other techniques for determining electrolyte physical and electrochemical properties (density, viscosity and ionic conductivity). The primary focus of the present work is on the difluoro(oxalato)borate (DFOB‒) anion and how the properties of this anion differ from other anions used in Li-ion battery electrolyte mixtures. The synthesis of highly pure LiDFOB is reported, along with the X-ray single crystal structural analysis of the neat salt and its dihydrate (LiDFOB∙2H2O). The ion ‒ ‒ coordination behavior of the DFOB anion is compared with the structurally similar BF4 and lithium bis(oxalato)borate (BOB‒) anions. The decomposition mechanism and Raman vibrational band assignments for the LiDFOB salt are also compared with those for LiBF4 and LiBOB.
    [Show full text]
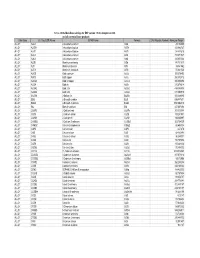
  • Database Full Listing
    16-Nov-06 OLI Data Base Listings for ESP version 7.0.46, Analyzers 2.0.46 and all current alliance products Data Base OLI Tag (ESP) Name IUPAC Name Formula CAS Registry Number Molecular Weight ALLOY AL2U 2-Aluminum uranium Al2U 291.98999 ALLOY AL3TH 3-Aluminum thorium Al3Th 312.982727 ALLOY AL3TI 3-Aluminum titanium Al3Ti 128.824615 ALLOY AL3U 3-Aluminum uranium Al3U 318.971527 ALLOY AL4U 4-Aluminum uranium Al4U 345.953064 ALLOY ALSB Aluminum antimony AlSb 148.731537 ALLOY ALTI Aluminum titanium AlTi 74.861542 ALLOY ALTI3 Aluminum 3-titanium AlTi3 170.621536 ALLOY AUCD Gold cadmium AuCd 309.376495 ALLOY AUCU Gold copper AuCu 260.512512 ALLOY AUCU3 Gold 3-copper AuCu3 387.604492 ALLOY AUSN Gold tin AuSn 315.676514 ALLOY AUSN2 Gold 2-tin AuSn2 434.386505 ALLOY AUSN4 Gold 4-tin AuSn4 671.806519 ALLOY BA2SN 2-Barium tin Ba2Sn 393.369995 ALLOY BI2U 2-Bismuth uranium Bi2U 655.987671 ALLOY BI4U3 4-Bismuth 3-uranium Bi4U3 1550.002319 ALLOY BIU Bismuth uranium BiU 447.007294 ALLOY CA2PB 2-Calcium lead Ca2Pb 287.355988 ALLOY CA2SI 2-Calcium silicon Ca2Si 108.241501 ALLOY CA2SN 2-Calcium tin Ca2Sn 198.865997 ALLOY CA3SB2 3-Calcium 2-antimony Ca3Sb2 363.734009 ALLOY CAMG2 Calcium 2-magnesium CaMg2 88.688004 ALLOY CAPB Calcium lead CaPb 247.278 ALLOY CASI Calcium silicon CaSi 68.163498 ALLOY CASI2 Calcium 2-silicon CaSi2 96.249001 ALLOY CASN Calcium tin CaSn 158.787994 ALLOY CAZN Calcium zinc CaZn 105.468002 ALLOY CAZN2 Calcium 2-zinc CaZn2 170.858002 ALLOY CD11U 11-Cadmium uranium Cd11U 1474.536865 ALLOY CD3AS2 3-Cadmium 2-arsenic As2Cd3 487.073212
    [Show full text]
  • The Microscopic Determination of the Nonopaque Minerals
    DEPARTMENT OF THE INTERIOR ALBERT B. FALL, Secretary UNITED STATES GEOLOGICAL SURVEY GEORGE OTIS SMITH, Director Bulletin 679 THE MICROSCOPIC DETERMINATION OF THE NONOPAQUE MINERALS BY ESPER S. LARSEN WASHINGTON GOVERNMENT PRINTING OFFICE 1921 CONTENTS. CHAPTER I. Introduction.................................................. 5 The immersion method of identifying minerals........................... 5 New data............................................................. 5 Need of further data.................................................... 6 Advantages of the immersion method.................................... 6 Other suggested uses for the method.................................... 7 Work and acknowledgments............................................. 7 CHAPTER II. Methods of determining the optical constants of minerals ....... 9 The chief optical constants and their interrelations....................... 9 Measurement of indices of refraction.................................... 12 The embedding method............................................ 12 The method of oblique illumination............................. 13 The method of central illumination.............................. 14 Immersion media.................................................. 14 General features............................................... 14 Piperine and iodides............................................ 16 Sulphur-selenium melts....................................... 38 Selenium and arsenic selenide melts........................... 20 Methods of standardizing
    [Show full text]
  • The Composition and Distribution of Phosphate Rock with Special Reference to the United States
    ~g 2 8 11111 . 1/11/2.5 2 5 ~g. ~~ IIIF8 11111 . 1.0 3 2 1.0 B;;;, 11111 . !;;j 1I111~J, 2;..; 2.2 !.;. 1'111361.1- :: IIIII~ 1'- I:" .... }9~ '- :: ;4,& 2.0 1.1 ...........'- - 1.1 !:...:: 11 111111.8 111111.25 111111.4 '""1.6 111111.25 11111_1.4 "'" 1.6 MICROCOPY RESOLUT'DN WiT CHART MICROCOPY RlSOLUTION TEST CHART NATIONAL BUREAU (1F SlANfJARDo 1%, A ~==~~==-~~~~====~==~~ TECHNICAL Bl'1.LETINNO.364~ JUNE 1933 UNITED STATES DEPARTMENT OF AGRICULTURE WASHING""'ON, D. C THE COMPOSITION AND DISTRIBUTION OF PHOS­ PHATE ROC ~~ WITH SPECIAL REFEREHCE TO THE UNITED STATES By K. D. JACOB, Chemist, and W. L. TrILL, H. L. MARSHALL, and D. S. REY­ NOJ.DS, Assill/ant Chem':sts, Division oj Fertiliz~ Technology, Fertili,~er and Fixed Nitrogen Investigations, Bu,real.<. of Chemistry and Soils.' CONTENT!'. Page Page Introductlou________________________________ 1 Methods of chemlc.nl analysis________________ ]7 ReviewStates _______________________of phosphate deposits •_of .the __________ Uuited _ Results of chemical analyses_._______________ 19 4 Pbosphoric acid __ •______ ._______________ 25 Alabama____________ .___ ._______________ _ 26 Arkansas_______________________________ _ 4 o.ilcium and magnesium________________ 4 .5Juminum, iron, and titanium••________ 26 Florlda_____ •_________ •_. ____ . __________ _ 4 Sodium and potassium________..________ 27 6 :Manganese, chromium, and vanadium__ 27 Copper, zinc, and arsenlc__________ ._ ____ 29 Illinois~e~~~~~:=::=::::::__________ •_____:::= •::::::::~:::::::::____ • __ ..________ 6 Kentucky__ ,___ ._.____ •___ •• __ •_________ 6 Barium,elements rare_______________________ earths, and other metallic•_______ 6 Silica and carbon dloxide _____• __________ 31 r. Fluorine_________ •________ •__________ •___ 32 32 Chlorine, brQmlne, and iodine._________ _ g:~~!~~~e:~~=~::=::::::::::~::::::::~::Nevada_________ ._._.__ •_______ ....
    [Show full text]