DOCSLIB.ORG

Normality Test in Clinical Research

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

pISSN: 2093-940X, eISSN: 2233-4718 Journal of Rheumatic Diseases Vol. 26, No. 1, January, 2019 https://doi.org/10.4078/jrd.2019.26.1.5 Review Article Normality Test in Clinical Research Sang Gyu Kwak1, Sung-Hoon Park2 1Department of Medical Statistics and 2Division of Rheumatology, Department of Internal Medicine, Catholic University of Daegu School of Medicine, Daegu, Korea In data analysis, given that various statistical methods assume that the distribution of the population data is normal distribution, it is essential to check and test whether or not the data satisfy the normality requirement. Although the analytical methods vary depending on whether or not the normality is satisfied, inconsistent results might be obtained depending on the analysis meth- od used. In many clinical research papers, the results are presented and interpreted without checking or testing normality. According to the central limit theorem, the distribution of the sample mean satisfies the normal distribution when the number of samples is above 30. However, in many clinical studies, due to cost and time restrictions during data collection, the number of samples is frequently lower than 30. In this case, a proper statistical analysis method is required to determine whether or not the normality is satisfied by performing a normality test. In this regard, this paper discusses the normality check, several methods of normality test, and several statistical analysis methods with or without normality checks. (J Rheum Dis 2019;26:5-11) Key Words. Normality check, Normal distribution, Normality test, Statistical analysis method INTRODUCTION Although the analytical method varies depending on whether or not the normality requirement is satisfied, in- In data analysis, given that various statistical methods consistent results might be obtained depending on the assume that the distribution of the population data is nor- analysis method used. Said differently, it can be con- mal distribution, it is essential to check and test whether cluded that two independent groups have the same dis- or not the data satisfy the normality requirement. For ex- tribution, although they are in fact different. On the other ample, when comparing the distribution of two in- hand, it can be concluded that the distribution of two in- dependent groups, two sample t-tests, which is a para- dependent groups is the same. In order to solve these metric method, are used, if the two population data sat- problems, it is necessary to check and test whether or not isfy the normality requirement, and the Mann-Whitney the normality requirement is satisfied. U-test, which is a nonparametric method, if the data do In many clinical research papers, results are presented not satisfy the normality requirement [1]. The two-sam- and interpreted without checking or testing normality. In ple t-test assumes normality and the Mann-Whitney the case when the reviewer requests the normality check U-test does not assume normality. If the data satisfy nor- or test in the review process of a thesis, the normality test mality, the distribution of the two groups can be com- is carried out to correct the contents of the submitted pared using a two-sample t-test using means and stand- papers. However, when this lack of the normality check or ard deviation. However, if normality is not satisfied, the test goes unnoticed, the results are frequently presented Mann-Whitney U-test is used, which does not use the without a normality test. If the statistical analysis method mean and standard deviation and concludes that the two assumes normality, a normality test should be performed groups are similar if the rankings are similar. to check whether or not the normality requirement is Received：August 22, 2018, Revised：September 14, 2018, Accepted：September 14, 2018 Corresponding to：Sung-Hoon Park http://orcid.org/0000-0002-3218-5420 Division of Rheumatology, Department of Internal Medicine, Catholic University of Daegu School of Medicine, 33 Duryugongwon-ro 17-gil, Nam-gu, Daegu 42472, Korea. E-mail：[email protected] Copyright ⓒ 2019 by The Korean College of Rheumatology. All rights reserved. This is a Open Access article, which permits unrestricted non-commerical use, distribution, and reproduction in any medium, provided the original work is properly cited. 5 Sang Gyu Kwak and Sung-Hoon Park satisfied. One of the reasons why normality tests are not However, when the difference value between the mean performed is that the researchers’ understanding of the and the median is big, the distribution is skewed to the statistical analysis methods is low. right or to the left. Furthermore, the average of the collected data is the sample mean. According to the central limit theorem, the 3) Skewness and kurtosis distribution of the sample mean satisfies the normal dis- Skewness is a measure of the “asymmetry” of the proba- tribution when the number of samples is larger than 30 bility distribution, in which the curve appears distorted or [2]. Therefore, if the number of samples is larger than 30, skewed either to the left or to the right. In a perfect nor- the analysis can be performed on the assumption that the mal distribution, the tails on either side of the curve are normality is satisfied. In clinical studies, however, the exact mirror images of each other. When a distribution is number of samples is frequently lower than 30. The rea- skewed to the left, the tail on the curve's left-hand side is sons for this scarcity of samples include cost and time re- longer than that on the right-hand side, and the mean is strictions during data collection. In this case, a proper less than the mode. This situation is also referred to as statistical analysis method is required to determine negative skewness. When a distribution is skewed to the whether or not the normality requirement is satisfied by right, the tail on the curve's right-hand side is longer than performing a normality test. the tail on the left-hand side, and the mean is greater than The remainder of this paper is structured as follows. the mode. This situation is also referred to as positive First, we introduce the contents of normality check, skewness. which is followed by the introduction of several methods Kurtosis is a measure of the “tailedness” of the proba- of normality test. In addition, some statistical analysis bility distribution, in which the tails asymptotically ap- methods that should be used when the normality require- proach zero or not. Distributions with zero excess kurto- ment is or is not satisfied are described for the data analy- sis are called mesokurtic or mesokurtotic. The most sis in clinical studies. prominent example of a mesokurtic distribution is nor- mal distribution. A distribution with a positive excess MAIN SUBJECTS kurtosis is called leptokurtic or leptokurtotic. In terms of shape, a leptokurtic distribution has fatter tails. Examples Normality check of leptokurtic distributions include the Student's t-dis- There are four methods to check whether or not the col- tribution, exponential distribution, Poisson distribution, lected data satisfy the normality requirement. These and the logistic distribution. A distribution with a neg- methods are checking the normality using plot and sev- ative excess kurtosis is called platykurtic or platykurtotic. eral statistics, such as mean, median, skewness, and Examples of platykurtic distributions include the con- kurtosis. tinuous or discrete uniform distributions and the raised cosine distribution. The most platykurtic distribution is 1) Distribution plot the Bernoulli distribution. A distribution plot of the collected data is useful to check normality of the data. The distribution of the data should 4) Q–Q plot be checked to determine that it does not deviate too much A Q–Q plot is a plot of the quantiles of two distributions as compared to the normal distribution. against each other, or a plot based on the estimates of the quantiles. The pattern of points in the plot is used to com- 2) Difference value between mean and median pare the two distributions. The main step in constructing The mean is a simple arithmetic average of the given set a Q–Q plot is calculating or estimating the quantiles to be of values or quantities. The median is a positional average plotted. If one or both of the axes in a Q–Q plot is based and is defined as the middle number in an ordered list of on a theoretical distribution with a continuous cumu- values. In a normal distribution, the graph appears as a lative distribution function (CDF), all quantiles are classical, symmetrical “bell-shaped curve.” The mean, or uniquely defined and can be obtained by inverting the average, and the mode, or maximum point on the curve, CDF. If a theoretical probability distribution with a dis- are equal. Hence, the difference value between the mean continuous CDF is one of the two compared dis- and the median are close to zero in normal distribution. tributions, some quantiles may not be defined, so an in- 6 J Rheum Dis Vol. 26, No. 1, January, 2019 Normality Test in Clinical Research terpolated quantile may be plotted. If the Q–Q plot is to draw conclusions whether or not the collected data sat- based on the data, there are multiple quantile estimators isfy the normality requirement. Only a rough guess can be in use. The rules for forming Q–Q plots when quantiles made as in this respect. Therefore, to the definite answer, must be estimated or interpolated are called plotting we have to consider a statistical test for normality. There positions. are several methods to perform a normality test. The A simple case is when there are two data sets of the same Kolmogorov-Smirnov test, the Shapiro-Wilk test, and the size.
Recommended publications
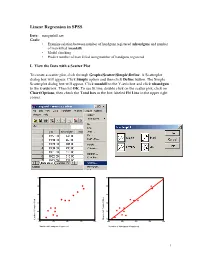
  • Linear Regression in SPSS

    Linear Regression in SPSS

    Linear Regression in SPSS Data: mangunkill.sav Goals: • Examine relation between number of handguns registered (nhandgun) and number of man killed (mankill) • Model checking • Predict number of man killed using number of handguns registered I. View the Data with a Scatter Plot To create a scatter plot, click through Graphs\Scatter\Simple\Define. A Scatterplot dialog box will appear. Click Simple option and then click Define button. The Simple Scatterplot dialog box will appear. Click mankill to the Y-axis box and click nhandgun to the x-axis box. Then hit OK. To see fit line, double click on the scatter plot, click on Chart\Options, then check the Total box in the box labeled Fit Line in the upper right corner. 60 60 50 50 40 40 30 30 20 20 10 10 Killed of People Number Number of People Killed 400 500 600 700 800 400 500 600 700 800 Number of Handguns Registered Number of Handguns Registered 1 Click the target button on the left end of the tool bar, the mouse pointer will change shape. Move the target pointer to the data point and click the left mouse button, the case number of the data point will appear on the chart. This will help you to identify the data point in your data sheet. II. Regression Analysis To perform the regression, click on Analyze\Regression\Linear. Place nhandgun in the Dependent box and place mankill in the Independent box. To obtain the 95% confidence interval for the slope, click on the Statistics button at the bottom and then put a check in the box for Confidence Intervals.
  • On the Meaning and Use of Kurtosis

    On the Meaning and Use of Kurtosis

    Psychological Methods Copyright 1997 by the American Psychological Association, Inc. 1997, Vol. 2, No. 3,292-307 1082-989X/97/$3.00 On the Meaning and Use of Kurtosis Lawrence T. DeCarlo Fordham University For symmetric unimodal distributions, positive kurtosis indicates heavy tails and peakedness relative to the normal distribution, whereas negative kurtosis indicates light tails and flatness. Many textbooks, however, describe or illustrate kurtosis incompletely or incorrectly. In this article, kurtosis is illustrated with well-known distributions, and aspects of its interpretation and misinterpretation are discussed. The role of kurtosis in testing univariate and multivariate normality; as a measure of departures from normality; in issues of robustness, outliers, and bimodality; in generalized tests and estimators, as well as limitations of and alternatives to the kurtosis measure [32, are discussed. It is typically noted in introductory statistics standard deviation. The normal distribution has a kur- courses that distributions can be characterized in tosis of 3, and 132 - 3 is often used so that the refer- terms of central tendency, variability, and shape. With ence normal distribution has a kurtosis of zero (132 - respect to shape, virtually every textbook defines and 3 is sometimes denoted as Y2)- A sample counterpart illustrates skewness. On the other hand, another as- to 132 can be obtained by replacing the population pect of shape, which is kurtosis, is either not discussed moments with the sample moments, which gives or, worse yet, is often described or illustrated incor- rectly. Kurtosis is also frequently not reported in re- ~(X i -- S)4/n search articles, in spite of the fact that virtually every b2 (•(X i - ~')2/n)2' statistical package provides a measure of kurtosis.
  • Regaining Normality: a Grounded Theory Study of the Illness

    Regaining Normality: a Grounded Theory Study of the Illness

    International Journal of Nursing Studies 93 (2019) 87–96 Contents lists available at ScienceDirect International Journal of Nursing Studies journal homepage: www.elsevier.com/ijns Regaining normality: A grounded theory study of the illness experiences of Chinese patients living with Crohn’s disease a,b a, Jiayin Ruan , Yunxian Zhou * a School of Nursing, Zhejiang Chinese Medical University, 548 Binwen Road, Binjiang District, Hangzhou, 310053, Zhejiang, China b Sir Run Run Shaw Hospital, Zhejiang University School of Medicine, 3 East Qingchun Road, 310016, Zhejiang, China A R T I C L E I N F O A B S T R A C T Article history: Background: Crohn’s disease is a chronic condition causing inflammation of the lining of the digestive Received 29 June 2018 system. Individuals suffering from this illness encounter various challenges and problems, but studies Received in revised form 19 February 2019 investigating the illness experiences of patients with Crohn’s disease in East Asian countries are scarce. Accepted 23 February 2019 Objectives: The objective of this study was to explore the illness experiences of patients with Crohn’s disease in China and construct an interpretive understanding of these experiences from the perspective of the patients. Keywords: Design: A constructivist grounded theory approach was used to develop a theoretical understanding of Crohn’s disease illness experiences. Grounded theory Settings: This study included participants from the following four provincial capital cities in China: Inflammatory bowel disease Hangzhou, Nanjing, Guangzhou, and Wuhan. Qualitative research Illness experiences Participants: Purposive sampling and theoretical sampling were used to select Chinese patients living with Crohn’s disease.
  • The Probability Lifesaver: Order Statistics and the Median Theorem

    The Probability Lifesaver: Order Statistics and the Median Theorem

    The Probability Lifesaver: Order Statistics and the Median Theorem Steven J. Miller December 30, 2015 Contents 1 Order Statistics and the Median Theorem 3 1.1 Definition of the Median 5 1.2 Order Statistics 10 1.3 Examples of Order Statistics 15 1.4 TheSampleDistributionoftheMedian 17 1.5 TechnicalboundsforproofofMedianTheorem 20 1.6 TheMedianofNormalRandomVariables 22 2 • Greetings again! In this supplemental chapter we develop the theory of order statistics in order to prove The Median Theorem. This is a beautiful result in its own, but also extremely important as a substitute for the Central Limit Theorem, and allows us to say non- trivial things when the CLT is unavailable. Chapter 1 Order Statistics and the Median Theorem The Central Limit Theorem is one of the gems of probability. It’s easy to use and its hypotheses are satisfied in a wealth of problems. Many courses build towards a proof of this beautiful and powerful result, as it truly is ‘central’ to the entire subject. Not to detract from the majesty of this wonderful result, however, what happens in those instances where it’s unavailable? For example, one of the key assumptions that must be met is that our random variables need to have finite higher moments, or at the very least a finite variance. What if we were to consider sums of Cauchy random variables? Is there anything we can say? This is not just a question of theoretical interest, of mathematicians generalizing for the sake of generalization. The following example from economics highlights why this chapter is more than just of theoretical interest.
  • Theoretical Statistics. Lecture 5. Peter Bartlett

    Theoretical Statistics. Lecture 5. Peter Bartlett

    Theoretical Statistics. Lecture 5. Peter Bartlett 1. U-statistics. 1 Outline of today’s lecture We’ll look at U-statistics, a family of estimators that includes many interesting examples. We’ll study their properties: unbiased, lower variance, concentration (via an application of the bounded differences inequality), asymptotic variance, asymptotic distribution. (See Chapter 12 of van der Vaart.) First, we’ll consider the standard unbiased estimate of variance—a special case of a U-statistic. 2 Variance estimates n 1 s2 = (X − X¯ )2 n n − 1 i n Xi=1 n n 1 = (X − X¯ )2 +(X − X¯ )2 2n(n − 1) i n j n Xi=1 Xj=1 n n 1 2 = (X − X¯ ) − (X − X¯ ) 2n(n − 1) i n j n Xi=1 Xj=1 n n 1 1 = (X − X )2 n(n − 1) 2 i j Xi=1 Xj=1 1 1 = (X − X )2 . n 2 i j 2 Xi<j 3 Variance estimates This is unbiased for i.i.d. data: 1 Es2 = E (X − X )2 n 2 1 2 1 = E ((X − EX ) − (X − EX ))2 2 1 1 2 2 1 2 2 = E (X1 − EX1) +(X2 − EX2) 2 2 = E (X1 − EX1) . 4 U-statistics Definition: A U-statistic of order r with kernel h is 1 U = n h(Xi1 ,...,Xir ), r iX⊆[n] where h is symmetric in its arguments. [If h is not symmetric in its arguments, we can also average over permutations.] “U” for “unbiased.” Introduced by Wassily Hoeffding in the 1940s. 5 U-statistics Theorem: [Halmos] θ (parameter, i.e., function defined on a family of distributions) admits an unbiased estimator (ie: for all sufficiently large n, some function of the i.i.d.
  • Lecture 14 Testing for Kurtosis

    Lecture 14 Testing for Kurtosis

    9/8/2016 CHE384, From Data to Decisions: Measurement, Kurtosis Uncertainty, Analysis, and Modeling • For any distribution, the kurtosis (sometimes Lecture 14 called the excess kurtosis) is defined as Testing for Kurtosis 3 (old notation = ) • For a unimodal, symmetric distribution, Chris A. Mack – a positive kurtosis means “heavy tails” and a more Adjunct Associate Professor peaked center compared to a normal distribution – a negative kurtosis means “light tails” and a more spread center compared to a normal distribution http://www.lithoguru.com/scientist/statistics/ © Chris Mack, 2016Data to Decisions 1 © Chris Mack, 2016Data to Decisions 2 Kurtosis Examples One Impact of Excess Kurtosis • For the Student’s t • For a normal distribution, the sample distribution, the variance will have an expected value of s2, excess kurtosis is and a variance of 6 2 4 1 for DF > 4 ( for DF ≤ 4 the kurtosis is infinite) • For a distribution with excess kurtosis • For a uniform 2 1 1 distribution, 1 2 © Chris Mack, 2016Data to Decisions 3 © Chris Mack, 2016Data to Decisions 4 Sample Kurtosis Sample Kurtosis • For a sample of size n, the sample kurtosis is • An unbiased estimator of the sample excess 1 kurtosis is ∑ ̅ 1 3 3 1 6 1 2 3 ∑ ̅ Standard Error: • For large n, the sampling distribution of 1 24 2 1 approaches Normal with mean 0 and variance 2 1 of 24/n 3 5 • For small samples, this estimator is biased D. N. Joanes and C. A. Gill, “Comparing Measures of Sample Skewness and Kurtosis”, The Statistician, 47(1),183–189 (1998).
  • Covariances of Two Sample Rank Sum Statistics

    Covariances of Two Sample Rank Sum Statistics

    JOURNAL OF RESEARCH of the National Bureou of Standards - B. Mathematical Sciences Volume 76B, Nos. 1 and 2, January-June 1972 Covariances of Two Sample Rank Sum Statistics Peter V. Tryon Institute for Basic Standards, National Bureau of Standards, Boulder, Colorado 80302 (November 26, 1971) This note presents an elementary derivation of the covariances of the e(e - 1)/2 two-sample rank sum statistics computed among aU pairs of samples from e populations. Key words: e Sample proble m; covariances, Mann-Whitney-Wilcoxon statistics; rank sum statistics; statistics. Mann-Whitney or Wilcoxon rank sum statistics, computed for some or all of the c(c - 1)/2 pairs of samples from c populations, have been used in testing the null hypothesis of homogeneity of dis­ tribution against a variety of alternatives [1, 3,4,5).1 This note presents an elementary derivation of the covariances of such statistics under the null hypothesis_ The usual approach to such an analysis is the rank sum viewpoint of the Wilcoxon form of the statistic. Using this approach, Steel [3] presents a lengthy derivation of the covariances. In this note it is shown that thinking in terms of the Mann-Whitney form of the statistic leads to an elementary derivation. For comparison and completeness the rank sum derivation of Kruskal and Wallis [2] is repeated in obtaining the means and variances. Let x{, r= 1,2, ... , ni, i= 1,2, ... , c, be the rth item in the sample of size ni from the ith of c populations. Let Mij be the Mann-Whitney statistic between the ith andjth samples defined by n· n· Mij= ~ t z[J (1) s=1 1' = 1 where l,xJ~>xr Zr~= { I) O,xj";;;x[ } Thus Mij is the number of times items in the jth sample exceed items in the ith sample.
  • A Robust Rescaled Moment Test for Normality in Regression

    A Robust Rescaled Moment Test for Normality in Regression

    Journal of Mathematics and Statistics 5 (1): 54-62, 2009 ISSN 1549-3644 © 2009 Science Publications A Robust Rescaled Moment Test for Normality in Regression 1Md.Sohel Rana, 1Habshah Midi and 2A.H.M. Rahmatullah Imon 1Laboratory of Applied and Computational Statistics, Institute for Mathematical Research, University Putra Malaysia, 43400 Serdang, Selangor, Malaysia 2Department of Mathematical Sciences, Ball State University, Muncie, IN 47306, USA Abstract: Problem statement: Most of the statistical procedures heavily depend on normality assumption of observations. In regression, we assumed that the random disturbances were normally distributed. Since the disturbances were unobserved, normality tests were done on regression residuals. But it is now evident that normality tests on residuals suffer from superimposed normality and often possess very poor power. Approach: This study showed that normality tests suffer huge set back in the presence of outliers. We proposed a new robust omnibus test based on rescaled moments and coefficients of skewness and kurtosis of residuals that we call robust rescaled moment test. Results: Numerical examples and Monte Carlo simulations showed that this proposed test performs better than the existing tests for normality in the presence of outliers. Conclusion/Recommendation: We recommend using our proposed omnibus test instead of the existing tests for checking the normality of the regression residuals. Key words: Regression residuals, outlier, rescaled moments, skewness, kurtosis, jarque-bera test, robust rescaled moment test INTRODUCTION out that the powers of t and F tests are extremely sensitive to the hypothesized error distribution and may In regression analysis, it is a common practice over deteriorate very rapidly as the error distribution the years to use the Ordinary Least Squares (OLS) becomes long-tailed.
  • Notes on the History of Normality Á Reflections on the Work of Quetelet

    Notes on the History of Normality Á Reflections on the Work of Quetelet

    Scandinavian Journal of Disability Research Vol. 8, No. 4, 232Á246, 2006 Notes on the History of Normality Reflections on the Work of QueteletÁ and Galton LARS GRUE* & ARVID HEIBERG** *Norwegian Social Research (NOVA), Oslo, Norway, **Department of Medical Genetics, Rikshospitalet, Oslo, Norway ABSTRACT This article investigates the historical background of our present understanding of normality and the hegemony of the empirical norm. This is an understanding that is closely linked to the development of eugenics, the rank ordering of human beings, the emergence of rehabilitation and the social construction of statistics within the social sciences. The article describes how the ideas of the Belgian statistician Adolphe Quetelet and his concept of the ‘‘average man’’, together the work of the Victorian polymath Francis Galton, who coined the term eugenics, have had lasting influence on how we today conceive the term normality. In the article brief historical glimpses into the birth of rehabilitation and the eugenic practices, which culminated with the killing of thousands of disabled people during the Nazi occupation of Europe are presented. Towards the end of the article it is questioned whether our present knowledge about inheritance and the genetic makeup of human beings can support the understandings leading to the concepts of normal and normality. Introduction In most countries, what might be referred to as the empirical norm, a term coined by the French historian Henri-Jacques Stiker (1999), and the principle of normalization, have long dominated policies for and the care of disabled people. Moser (2000) has pointed out that the normalization approach is constantly counteracted by processes that systematically produce inequality and reproduce exclusions.
  • Testing Normality: a GMM Approach Christian Bontempsa and Nour

    Testing Normality: a GMM Approach Christian Bontempsa and Nour

    Testing Normality: A GMM Approach Christian Bontempsa and Nour Meddahib∗ a LEEA-CENA, 7 avenue Edouard Belin, 31055 Toulouse Cedex, France. b D´epartement de sciences ´economiques, CIRANO, CIREQ, Universit´ede Montr´eal, C.P. 6128, succursale Centre-ville, Montr´eal (Qu´ebec), H3C 3J7, Canada. First version: March 2001 This version: June 2003 Abstract In this paper, we consider testing marginal normal distributional assumptions. More precisely, we propose tests based on moment conditions implied by normality. These moment conditions are known as the Stein (1972) equations. They coincide with the first class of moment conditions derived by Hansen and Scheinkman (1995) when the random variable of interest is a scalar diffusion. Among other examples, Stein equation implies that the mean of Hermite polynomials is zero. The GMM approach we adopt is well suited for two reasons. It allows us to study in detail the parameter uncertainty problem, i.e., when the tests depend on unknown parameters that have to be estimated. In particular, we characterize the moment conditions that are robust against parameter uncertainty and show that Hermite polynomials are special examples. This is the main contribution of the paper. The second reason for using GMM is that our tests are also valid for time series. In this case, we adopt a Heteroskedastic-Autocorrelation-Consistent approach to estimate the weighting matrix when the dependence of the data is unspecified. We also make a theoretical comparison of our tests with Jarque and Bera (1980) and OPG regression tests of Davidson and MacKinnon (1993). Finite sample properties of our tests are derived through a comprehensive Monte Carlo study.
  • Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests

    Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests

    Journal ofStatistical Modeling and Analytics Vol.2 No.I, 21-33, 2011 Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests Nornadiah Mohd Razali1 Yap Bee Wah 1 1Faculty ofComputer and Mathematica/ Sciences, Universiti Teknologi MARA, 40450 Shah Alam, Selangor, Malaysia E-mail: nornadiah@tmsk. uitm. edu.my, yapbeewah@salam. uitm. edu.my ABSTRACT The importance of normal distribution is undeniable since it is an underlying assumption of many statistical procedures such as I-tests, linear regression analysis, discriminant analysis and Analysis of Variance (ANOVA). When the normality assumption is violated, interpretation and inferences may not be reliable or valid. The three common procedures in assessing whether a random sample of independent observations of size n come from a population with a normal distribution are: graphical methods (histograms, boxplots, Q-Q-plots), numerical methods (skewness and kurtosis indices) and formal normality tests. This paper* compares the power offour formal tests of normality: Shapiro-Wilk (SW) test, Kolmogorov-Smirnov (KS) test, Lillie/ors (LF) test and Anderson-Darling (AD) test. Power comparisons of these four tests were obtained via Monte Carlo simulation of sample data generated from alternative distributions that follow symmetric and asymmetric distributions. Ten thousand samples ofvarious sample size were generated from each of the given alternative symmetric and asymmetric distributions. The power of each test was then obtained by comparing the test of normality statistics with the respective critical values. Results show that Shapiro-Wilk test is the most powerful normality test, followed by Anderson-Darling test, Lillie/ors test and Kolmogorov-Smirnov test. However, the power ofall four tests is still low for small sample size.
  • Sexuality Across the Lifespan Childhood and Adolescence Introduction

    Sexuality Across the Lifespan Childhood and Adolescence Introduction

    Topics in Human Sexuality: Sexuality Across the Lifespan Childhood and Adolescence Introduction Take a moment to think about your first sexual experience. Perhaps it was “playing doctor” or “show me yours and I’ll show you mine.” Many of us do not think of childhood as a time of emerging sexuality, although we likely think of adolescence in just that way. Human sexual development is a process that occurs throughout the lifespan. There are important biological and psychological aspects of sexuality that differ in children and adolescents, and later in adults and the elderly. This course will review the development of sexuality using a lifespan perspective. It will focus on sexuality in infancy, childhood and adolescence. It will discuss biological and psychological milestones as well as theories of attachment and psychosexual development. Educational Objectives 1. Describe Freud’s theory of psychosexual development 2. Discuss sexuality in children from birth to age two 3. Describe the development of attachment bonds and its relationship to sexuality 4. Describe early childhood experiences of sexual behavior and how the child’s natural sense of curiosity leads to sexual development 5. Discuss common types of sexual play in early childhood, including what is normative 6. Discuss why it is now thought that the idea of a latency period of sexual development is inaccurate 7. Discuss differences in masturbation during adolescence for males and females 8. List and define the stages of Troiden’s model for development of gay identity 9. Discuss issues related to the first sexual experience 10. Discuss teen pregnancy Freud’s Contributions to Our Understanding of Sexual Development Prior to 1890, it was widely thought that sexuality began at puberty.