Ge1-Xsnx and Sn-P Quantum Dots
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Aerosolassisted CVD of Cadmium Diselenoimidodiphosphinate And
Aerosol-assisted CVD of cadmium diselenoimidodiphosphinate and formation of a new iPr2N2P3+ ion supported by combined DFT and mass spectrometric studies Oyetunde, T, Afzaal, M, Vincent, M and O'Brien, P http://dx.doi.org/10.1039/C6DT03186B Title Aerosol-assisted CVD of cadmium diselenoimidodiphosphinate and formation of a new iPr2N2P3+ ion supported by combined DFT and mass spectrometric studies Authors Oyetunde, T, Afzaal, M, Vincent, M and O'Brien, P Type Article URL This version is available at: http://usir.salford.ac.uk/id/eprint/40726/ Published Date 2016 USIR is a digital collection of the research output of the University of Salford. Where copyright permits, full text material held in the repository is made freely available online and can be read, downloaded and copied for non-commercial private study or research purposes. Please check the manuscript for any further copyright restrictions. For more information, including our policy and submission procedure, please contact the Repository Team at: [email protected]. Please do not adjust margins Journal Name ARTICLE Aerosol-assisted CVD of cadmium diselenoimidodiphosphinate i + and formation of a new Pr2N2P3 ion supported by combined DFT and mass spectrometric studies Received 00th January 20xx, Accepted 00th January 20xx Temidayo Oyetunde,a Mohammad Afzaal,b Mark A. Vincent,c and Paul O’Brien*d DOI: 10.1039/x0xx00000x i Aerosol-assisted chemical vapour deposition (AACVD) of Cd[(SeP Pr2)2N]2 is shown to deposit cadmium selenide and/or www.rsc.org/ cadmium phosphide on glass substrates, dependent upon the growth conditions. The phase, structure, morphology and composition of the films were characterised by X-ray powder diffraction (XRD), scanning electron microscopy, energy dispersive X-ray analysis and X-ray photoelectron spectroscopy. -

Chemical Names and CAS Numbers Final
Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number C3H8O 1‐propanol C4H7BrO2 2‐bromobutyric acid 80‐58‐0 GeH3COOH 2‐germaacetic acid C4H10 2‐methylpropane 75‐28‐5 C3H8O 2‐propanol 67‐63‐0 C6H10O3 4‐acetylbutyric acid 448671 C4H7BrO2 4‐bromobutyric acid 2623‐87‐2 CH3CHO acetaldehyde CH3CONH2 acetamide C8H9NO2 acetaminophen 103‐90‐2 − C2H3O2 acetate ion − CH3COO acetate ion C2H4O2 acetic acid 64‐19‐7 CH3COOH acetic acid (CH3)2CO acetone CH3COCl acetyl chloride C2H2 acetylene 74‐86‐2 HCCH acetylene C9H8O4 acetylsalicylic acid 50‐78‐2 H2C(CH)CN acrylonitrile C3H7NO2 Ala C3H7NO2 alanine 56‐41‐7 NaAlSi3O3 albite AlSb aluminium antimonide 25152‐52‐7 AlAs aluminium arsenide 22831‐42‐1 AlBO2 aluminium borate 61279‐70‐7 AlBO aluminium boron oxide 12041‐48‐4 AlBr3 aluminium bromide 7727‐15‐3 AlBr3•6H2O aluminium bromide hexahydrate 2149397 AlCl4Cs aluminium caesium tetrachloride 17992‐03‐9 AlCl3 aluminium chloride (anhydrous) 7446‐70‐0 AlCl3•6H2O aluminium chloride hexahydrate 7784‐13‐6 AlClO aluminium chloride oxide 13596‐11‐7 AlB2 aluminium diboride 12041‐50‐8 AlF2 aluminium difluoride 13569‐23‐8 AlF2O aluminium difluoride oxide 38344‐66‐0 AlB12 aluminium dodecaboride 12041‐54‐2 Al2F6 aluminium fluoride 17949‐86‐9 AlF3 aluminium fluoride 7784‐18‐1 Al(CHO2)3 aluminium formate 7360‐53‐4 1 of 75 Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number Al(OH)3 aluminium hydroxide 21645‐51‐2 Al2I6 aluminium iodide 18898‐35‐6 AlI3 aluminium iodide 7784‐23‐8 AlBr aluminium monobromide 22359‐97‐3 AlCl aluminium monochloride -

THE MONATOMIC IONS! 1. What Is the Formula for Silver? Ag 2. What Is
Name: ______________________________ THE MONATOMIC IONS! 1. What is the formula for silver? Ag+ 22. What is the formula for cobalt (II)? Co2+ 2. What is the formula for cadmium? Cd2+ 23. What is the formula for chromium (II)? Cr2+ 3. What is the formula for manganese (II)? Mn2+ 24. What is the formula for copper (II)? Cu2+ 4. What is the formula for nickel (II)? Ni2+ 25. What is the formula for tin (IV)? Sn4+ 5. What is the formula for chromous? Cr2+ 26. What is the formula for lead (IV)? Pb4+ 6. What is the formula for zinc? Zn2+ 27. What is the formula for iron (III)? Fe3+ 2+ 2+ 7. What is the formula for cobaltous? Co 28. What is the formula for mercury (I)? Hg2 8. What is the formula for cuprous? Cu+ 29. What is the formula for lead (II)? Pb2+ 9. What is the formula for ferrous? Fe2+ 30. What is the formula for mercury (II)? Hg2+ 2+ 2+ 10. What is the formula for mercurous? Hg2 31. What is the formula for iron (II)? Fe 11. What is the formula for stannous? Sn2+ 32. What is the formula for copper (I)? Cu+ 12. What is the formula for plumbous? Pb2+ 33. What is the formula for tin (II)? Sn2+ 13. What is the formula for chromic? Cr3+ 34. What is the formula for fluoride? F- 14. What is the formula for cobaltic? Co3+ 35. What is the formula for chloride? Cl- 15. What is the formula for cupric? Cu2+ 36. What is the formula for hydride? H- 16. -

Semiconductor and Magnetic Material 3
Semiconductor and 11 Magnetic Material 2 Electronic Devices Circuits and Applications 1.1 INTRODUCTION Semiconductors are materials having electrical conductivities between those of good conductors and insulators. Semiconductors resistivity varies from 10–5 to 10+4 m. Similarly resistivity range values 10–8 to 10+6 m for conductors and from 107 to 108 m for insulators. Germanium (Ge) and Silicon (Si) are the most commonly used semiconductors and belong to Group-IV of the periodic table. They have resistivity of about 0.6 and 1.5 × 103 m respectively. Also there are certain compound semiconductors such as gallium arsenide (GaAs), indium phosphide (InP), cadmium sulphide (CdS), etc. They are formed by the combination of the elements of groups III and V. Small band gap is another important characteristic of semiconductors. Also the semiconductors have negative temperature coefficient of resistance because the number of carriers in a semiconductor will increase significantly with temperature, resulting in reduction of the resistance of the semiconductor. 1.2 SEMICONDUCTOR MATERIALS (GROUP-IV) Semiconductors are materials having electrical conductivities between those of good conductors and insulators. The elemental semiconductor such as germanium (Ge) and silicon (Si) belong to Group-IV of the periodic table and have resistivity of about 0.6 and 1.5 × 103 cm respectively. The energy band gaps of these elements of Group-IV at 0 K are given as below: C (diamond) → 5.51 eV Ge → 0.75 eV Si → 1.16 eV Sn (grey) → 0.08 eV Pd → ≈ eV We may say from above list that at room temperature (i.e., 0 K) diamond behaves as an insulator but Ge and Si are treated as semiconductors. -

Sem Icond Uctors: Data Handbook
Otfried Madelung Sem icond uctors: Data Handbook 3rdedition Springer Short table of contents (for a more detailed table of contents see the following pages) A Introduction 1 General remarks to the structure of the volume .................................................................................... 1 2 Physical quantities tabulated in this volume ......................................................................................... 2 B Tetrahedrally bonded elements and compounds 1 Elements ofthe IVth group and IV-IV compounds ................................................ ....................... 7 2 111-V compounds .................................................................. 3 11-VI compounds ..................................................................................................... 4 I-VI1 compounds .................................................. ...................................................... 245 5 II12-V13 compounds .................................................................................................. 6 I-III-V12 compounds ..................................................................... 7 II-IV-V2 compounds ......................... ............................................................................... 329 8 I2-IV-VI3 compounds .......................................................................... ............................. 359 9 13-V-vI4 compounds ......................... ...................................................................................... 367 -
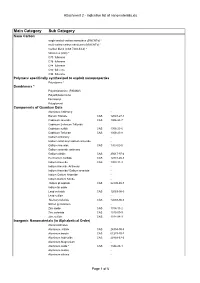
Attachment 2 - Indicative List of Nanomaterials.Xls
Attachment 2 - Indicative list of nanomaterials.xls Main Category Sub Category Nano Carbon single-walled carbon nanotubes (SWCNTs) * multi-walled carbon nanotubes (MWCNTs) * Carbon black (CAS 7440-44-0) * fullerenes (C60) * C70 fullerene C76 fullerene C84 fullerene C90 fullerene C94 fullerene Polymers specifically synthesized to exploit nanoproperties Polystyrene * Dendrimers * Polyamidoamine (PAMAM) Polyethylene imine Ferrocenyl Polyglycerol Components of Quantum Dots Aluminum Antinomy - Barium Titanate CAS 12047-27-7 Cadmium selenide CAS 1306-24-7 Cadmium Selenium Telluride Cadmium sulfide CAS 1306-23-6 Cadmium Telluride CAS 1306-25-8 Gallium Antimony - Gallium antimony/ Gallium arsenide - Gallium Arsenide CAS 1303-00-0 Gallium arsenide antimony Gallium nitride CAS 25617-97-4 Germanium carbide CAS 12334-26-8 Indium Arsenide CAS 1303-11-3 Indium Arsenide Antimony - Indium Arsenide/ Gallium arsenide - Indium Gallium Arsenide - Indium Gallium Nitride - Indium phosphide CAS 22398-80-7 Indium tin oxide - Lead selenide CAS 12069-00-0 Lead sulfide - Mercury telluride CAS 12068-90-5 Silicon germanium - Zinc oxide CAS 1314-13-2 Zinc selenide CAS 1315-09-9 Zinc sulfide CAS 1314-98-3 Inorganic Nanomaterials (in Alphabetical Order) Aluminosilicates - Aluminum nitride CAS 24304-00-5 Aluminum borate CAS 61279-70-7 Aluminum hydroxide CAS 20768-67-6 Aluminum Magnesium - Aluminum oxide * CAS 1344-28-1 Aluminum oxides - Aluminum silicate - Page 1 of 6 Attachment 2 - Indicative list of nanomaterials.xls Main Category Sub Category Aluminum Titanium Oxide -

List of Semiconductor Materials - Wikipedia, the Free Encyclopedia Page 1 of 4
List of semiconductor materials - Wikipedia, the free encyclopedia Page 1 of 4 List of semiconductor materials From Wikipedia, the free encyclopedia Semiconductor materials are insulators at absolute zero temperature that conduct electricity in a limited way at room temperature. The defining property of a semiconductor material is that it can be doped with impurities that alter its electronic properties in a controllable way. Because of their application in devices like transistors (and therefore computers) and lasers, the search for new semiconductor materials and the improvement of existing materials is an important field of study in materials science. The most commonly used semiconductor materials are crystalline inorganic solids. These materials can be classified according to the periodic table groups from which their constituent atoms come. Semiconductor materials are differing by their properties. Compound semiconductors have advantages and disadvantages in comparison with silicon. For example gallium arsenide has six times higher electron mobility than silicon, which allows faster operation; wider band gap, which allows operation of power devices at higher temperatures, and gives lower thermal noise to low power devices at room temperature; its direct band gap gives it more favorable optoelectronic properties than the indirect band gap of silicon; it can be alloyed to ternary and quaternary compositions, with adjustable band gap width, allowing light emission at chosen wavelengths, and allowing e.g. matching to wavelengths with lowest losses in optical fibers. GaAs can be also grown in a semiinsulating form, which is suitable as a lattice-matching insulating substrate for GaAs devices. Conversely, silicon is robust, cheap, and easy to process, while GaAs is brittle, expensive, and insulation layers can not be created by just growing an oxide layer; GaAs is therefore used only where silicon is not sufficient.[1] Some materials can be prepared with tunable properties, e.g. -
Curriculum Vitae
CURRICULUM VITAE William E. Buhro December 3, 2010 Mailing Washington University Address: Department of Chemistry Campus Box 1134 1 Brookings Drive St. Louis, MO 63130-4899 (314) 935-4269 FAX (314) 935-4481 [email protected] Personal: Born March 20, 1958 in Lansing, Michigan. Married, with two sons. Education: A.B., magna cum laude in Chemistry, Hope College, Holland, Michigan, 1980. Undergraduate Research Advisor: Distinguished Professor Michael P. Doyle Ph.D., University of California, Los Angeles, 1985 Thesis Title: "Synthesis, Structure and Reactivity of Formaldehyde, Thioformaldehyde, and Phosphide Complexes of Rhenium" Thesis Advisor: Professor John A. Gladysz Professional 2010 – present Chair, Department of Chemistry, History: Washington University, St. Louis, MO. 2006 – present George E. Pake Professor in Arts & Sciences, Washington University, St. Louis, MO. 2004 – 2010 Associate Director, Center for Materials Innovation Washington University, St. Louis, MO. 2001 - 2006 Professor of Chemistry, Washington University, St. Louis, MO. 1993 - 2001 Associate Professor of Chemistry, Washington University, St. Louis, MO. 1987 - 1993 Assistant Professor of Chemistry, Washington University, St. Louis, MO. 1985 - 1987 Postdoctoral Fellow, Indiana University, Bloomington, Indiana. Advisor: Distinguished Professor Malcolm H. Chisholm. 1 Honors: Fellow of the American Chemical Society, 2010- St. Louis Award, St. Louis Section, American Chemical Society, 2010 Chair, Inorganic Chemistry Gordon Research Conference, 2007 Editor, Chemistry of Materials, 2005- Associate Editor, Chemistry of Materials, 2002-2005 Secretary, Division of Inorganic Chemistry, ACS, 2005-2007 Chair, Solid-State Subdivision, Division of Inorganic Chemistry, ACS, 2003 Member, International Advisory Editorial Board, Dalton Transactions, 2001-2007 Member, Board of Editors, Chemistry of Materials, 1998-2002 Member, Board of Editors, Inorganic Chemistry, 1997-1998 Emerson Electric Co. -

Elucidating the Location of Cd2+ in Post-Synthetically Treated Inp Quantum Dots Using Dynamic Nuclear Polarization 31P and 113Cd Solid-State NMR Spectroscopy
Chemistry Publications Chemistry 2-11-2021 Elucidating the Location of Cd2+ in Post-synthetically Treated InP Quantum Dots Using Dynamic Nuclear Polarization 31P and 113Cd Solid-State NMR Spectroscopy Michael P. Hanrahan Iowa State University and Ames Laboratory, [email protected] Jennifer L. Stein University of Washington Nayon Park University of Washington Brandi M. Cossairt University of Washington Aaron J. Rossini Iowa State University and Ames Laboratory, [email protected] Follow this and additional works at: https://lib.dr.iastate.edu/chem_pubs Part of the Materials Chemistry Commons, Nanoscience and Nanotechnology Commons, and the Physical Chemistry Commons The complete bibliographic information for this item can be found at https://lib.dr.iastate.edu/ chem_pubs/1289. For information on how to cite this item, please visit http://lib.dr.iastate.edu/ howtocite.html. This Article is brought to you for free and open access by the Chemistry at Iowa State University Digital Repository. It has been accepted for inclusion in Chemistry Publications by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Elucidating the Location of Cd2+ in Post-synthetically Treated InP Quantum Dots Using Dynamic Nuclear Polarization 31P and 113Cd Solid-State NMR Spectroscopy Abstract Indium phosphide quantum dots (InP QD) are a promising alternative to traditional QD materials that contain toxic heavy elements such as lead and cadmium. However, InP QD obtained from colloidal synthesis are often plagued by poor photoluminescence quantum yields (PL-QYs). In order to improve the PL-QY of InP QD, a number of post-synthetic treatments have been devised. -

Seeded Growth of Nanoscale Semiconductor Tetrapods: Generality and the Role of Cation Exchange Michael J
pubs.acs.org/cm Article Seeded Growth of Nanoscale Semiconductor Tetrapods: Generality and the Role of Cation Exchange Michael J. Enright, Florence Y. Dou, Shenwei Wu, Emily J. Rabe, Madison Monahan, Max R. Friedfeld, Cody W. Schlenker, and Brandi M. Cossairt* Cite This: Chem. Mater. 2020, 32, 4774−4784 Read Online ACCESS Metrics & More Article Recommendations *sı Supporting Information ABSTRACT: Nanoscale tetrapods were synthesized with inde- pendently tunable core and arm sizes and aspect ratios from a spectrum of quantum dot seeds, including ZnTe, CuInS2, InP, − − − − InP/ZnS, and Cd3P2. The range of II VI, I III VI, III V, and II−V seeds included both cubic and tetragonal lattices, demonstrating the versatility of CdS arm growth upon surfaces with accessible (111) planes, including those with distorted those with distorted structures. Except for the Cd3P2 seeds, where the effect is inconsequential, cation exchange in the core was observed to occur concurrently with arm growth to give alloyed cores in the final tetrapods. This result supports recent work characterizing the composition of core/shell quantum dots composed of distinct cations and presents a challenge to achieving clean interfaces in nanoscale semiconductor heterostructures grown by using traditional solvothermal methods. Conversely, the robust Cd3P2/CdS tetrapod architecture represents a rare example of near-infrared (NIR) emission in a multipod heterostructure. NIR-emissive tetrapod heterostructures were successfully obtained from Cd3P2 cores in combination with both high and low aspect ratio CdS arms. ■ INTRODUCTION a core/shell system, the handles for modulating the optoelectronic properties are limited since core size and shell The synthesis of nanomaterials of various shapes and sizes is 24,34,37,38 well established, and the importance of size and structure thickness are the primary tunable parameters. -

Common Product Name Hkhs Code "Kevlar" Polyamides Filament Yarn High Tenacity More Than 60Cn/Tex
COMMON PRODUCT NAME HKHS CODE "KEVLAR" POLYAMIDES FILAMENT YARN HIGH TENACITY MORE THAN 60CN/TEX. 54021100 "LYCRA" ELASTANE YARN (100% POLYURETHANE FILAMENT SINGLE YARN) 54024410 {O-2-(DIALKYL AMINO ETHYL} HYDROGEN ALKYL PHOSPHONITES AND THEIR O-ALKYL 29310007 ESTERS; ALKYLATED OR PROTONATED SALTS THEREOF {S-2-(DIALKYL AMINO) ETHYL} HYDROGEN ALKYL PHOSPHONOTHIOATES AND THEIR O- 29309001 ALKYL ESTERS; ALKYLATED OR PROTONATED SALTS THEREOF 0,0-DIETHYL S-{2-(DIETHYLAMINO) ETHYL} PHOSPHOROTHIOATE AND ITS ALKYLATED OR 29309011 PROTONATED SALTS 0-ALKYL (< OR = C10, INCLUDING CYCLOALKYL) ALKYL (METHYL, ETHYL, N-PROPYL OR 29310001 ISOPROPYL) PHOSPHONOFLUORIDATES 1 1 1-TRICHLOROETHANE 29031910 1 1-DICHLORO-1-FLUOROETHANE 29034908 1 1-DICHLORO-2 2 2-TRIFLUOROETHANE 29034904 1 2-DICHLOROETHYLENE 29032900 1-(1,3-BENZODIOXOL-5-YL)PROPAN-2-ONE 29329200 1,1 - DIFLUOROETHANE (HFC-152A) 29033946 1,1,1 - TRIFLUOROETHANE (HFC-143A) 29033945 1,1,1,2,2,3,4,5,5,5 - DECAFLUOROPENTANE (HFC-43-10MEE) 29033943 1,1,1,2,3,3,3-HEPTAFLUOROPROPANE 29033951 1,1,1,2-TETRAFLUOROETHANE 29033920 1,1,1,3,3 - PENTAFLUOROPROPANE (HFC-245FA) 29033954 1,1,1,3,3,3 - HEXAFLUOROPROPANE (HFC-236FA) 29033952 1,1,1-TRICHLOROETHANE 29031910 1,1,2,2,3 - PENTAFLUOROPROPANE (HFC-245CA) 29033953 1,1,3,3,3-PENTAFLUORO-2-(TRIFLUOROMETHYL) PROP-1-ENE 29033910 1,2-BIS (2-CHLOROETHYLTHIO) ETHANE 29309005 1,3-BIS (2-CHLOROETHYLTHIO) -N-PROPANE 29309006 1,4-BIS (2-CHLOROETHYLTHIO) -N-BUTANE 29309007 1,5-BIS (2-CHLOROETHYLTHIO) -N-PENTANE 29309008 1.8 M/M 65%POLYESTER STAPLE FIBRE 35%RAYON STAPLE FIBRE YARN DYED IN HANK 55095100 1/16NM 100%TRUE HEMP R.W. -

Semiconductors: Data Handbook H Springer-Verlag Berlin Heidelberg Gmbh Otfried Madelung
Semiconductors: Data Handbook H Springer-Verlag Berlin Heidelberg GmbH Otfried Madelung Semiconductors: Data Handbook 3rd edition 123 Proff. Dr. Ot frie d Madelung Am Kornacker 18 35041 Marburg Germany The 1st ed. was published in 2 volumes in the series “Data in Science and Technology”. The 2nd revised ed. was published under title “Semiconductors – Basic Data” . Additional material to this book can be downloaded from http://extras.springer.com ISBN 978-3-642-62332-5 ISBN 978-3-642-18865-7 (eBook) DOI 10.1007/978-3-642-18865-7 Cataloging-in-Publication Data appliedf fof r Bibliographic infformation published by Die Deutsche Bibliothek Die Deutsche Bibliothek lists this publication in the Deutsche Nationalbibliograffie ; detailed bibliographic data is available in the Internet at <http://dnb.ddb.de>. This work is subject to copyright. All rights are reserved, whether the whole or part of tfhe material is concerned, speciffically the rights off trans lation, reprinting, reuse of if llustrations, recitation, broadcasting, reproduction on microfiff lm or in other ways, and storage in data banks. Duplication of tfhis publication or parts thereof is permitte d only under the provisions of tfhe German Copyright Law offSeptem ber 9, 1965, in its current version, and permission for use must always be obtained from Springer-Verlag..Vio lations are liable for prosecution under German Copyright Lawaaw .w © Springer-Verlag Berlin Heidelberg 1991, 1992, 1996, and 2004 Originally published by Springer-Verlag Berlin Heidelberg New York in 2004 Softcover reprint of the hardcover 3rd edition 2004 http://www.springeronline.com The use of general descriptive names, registered names, trademarks,, etc.