DOCSLIB.ORG

Generative Adversarial Networks for Text Using Word2vec Intermediaries

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Generative Adversarial Networks for Text Using Word2vec Intermediaries Generative Adversarial Networks for text using word2vec intermediaries Akshay Budhkar1, 2, 4, Krishnapriya Vishnubhotla1, Safwan Hossain1, 2 and Frank Rudzicz1, 2, 3, 5 1Department of Computer Science, University of Toronto fabudhkar, vkpriya, [email protected] 2Vector Institute [email protected] 3St Michael’s Hospital 4Georgian Partners 5Surgical Safety Technologies Inc. Abstract the information to improve, however, if at the cur- rent stage of training it is not doing that yet, the Generative adversarial networks (GANs) have gradient of G vanishes. Additionally, with this shown considerable success, especially in the loss function, there is no correlation between the realistic generation of images. In this work, we apply similar techniques for the generation metric and the generation quality, and the most of text. We propose a novel approach to han- common workaround is to generate targets across dle the discrete nature of text, during training, epochs and then measure the generation quality, using word embeddings. Our method is ag- which can be an expensive process. nostic to vocabulary size and achieves compet- W-GAN (Arjovsky et al., 2017) rectifies these itive results relative to methods with various issues with its updated loss. Wasserstein distance discrete gradient estimators. is the minimum cost of transporting mass in con- 1 Introduction verting data from distribution Pr to Pg. This loss forces the GAN to perform in a min-max, rather Natural Language Generation (NLG) is often re- than a max-min, a desirable behavior as stated in garded as one of the most challenging tasks in (Goodfellow, 2016), potentially mitigating mode- computation (Murty and Kabadi, 1987). It in- collapse problems. The loss function is given by: volves training a model to do language genera- tion for a series of abstract concepts, represented either in some logical form or as a knowledge Lcritic = min max(Ex∼pr(x)[D(x)] base. Goodfellow introduced generative adver- G D2D (1) −E [D(~x)]) sarial networks (GANs) (Goodfellow et al., 2014) x~∼pg(x) as a method of generating synthetic, continuous data with realistic attributes. The model includes a where D is the set of 1-Lipschitz functions and discriminator network (D), responsible for distin- Pg is the model distribution implicitly defined by guishing between the real and the generated sam- x~ = G(z), z ∼ p(z). A differentiable function is ples, and a generator network (G), responsible for 1-Lipschtiz iff it has gradients with norm at most generating realistic samples with the goal of fool- 1 everywhere. Under an optimal D minimizing ing the D. This setup leads to a minimax game the value function with respect to the generator pa- where we maximize the value function with re- rameters minimizes the W(pr; pg), where W is the spect to D, and minimize it with respect to G. The Wasserstein distance, as discussed in (Vallender, ideal optimal solution is the complete replication 1974). To enforce the Lipschitz constraint, the au- of the real distributions of data by the generated thors propose clipping the weights of the gradient distribution. within a compact space [−c; c]. GANs, in this original setup, often suffer from (Gulrajani et al., 2017) show that even though the problem of mode collapse - where the G man- this setup leads to more stable training compared ages to find a few modes of data that resem- to the original GAN loss function, the architec- ble real data, using them consistently to fool the ture suffers from exploding and vanishing gradient D. Workarounds for this include updating the problems. They introduce the concept of gradient loss function to incorporate an element of multi- penalty as an alternative way to enforce the Lip- diversity. An optimal D would provide G with schitz constraint, by penalizing the gradient norm 15 Proceedings of the 4th Workshop on Representation Learning for NLP (RepL4NLP-2019), pages 15–26 Florence, Italy, August 2, 2019. c 2019 Association for Computational Linguistics directly in the loss. The loss function is given by: sentence generation by leaking high-level infor- mation from D to G, and generates a latent rep- resentation from the features of the already gen- 2 L = Lcritic + λEx^∼p(^x)[(jjrx^D(^x)jj2 − 1) ] (2) erated words, to aid in the next word generation. TextGAN (Zhang et al., 2017) adds an element of where x^ are random samples drawn from Px, diversity to the original GAN loss by employing and Lcritic is the loss defined in Equation1. the Maximum Mean Discrepancy objective to al- Empirical results of GANs over the past year or leviate mode collapse. so have been impressive. GANs have gotten state- In the latter half of 2018, (Zhu et al., 2018) in- of-the-art image-generation results on datasets like troduced Texygen, a benchmarking platform for ImageNet (Brock et al., 2018) and LSUN (Rad- natural language generation, while introducing ford et al., 2015). Such GANs are fully differen- standard metrics apt for this task. (Lu et al., 2018) tiable and allow for back-propagation of gradients surveys all these new methods along with other from D through the samples generated by G. How- baselines, and documents model performance on ever, if the data is discrete, as, in the case of text, standard corpus like EMNLP2017 WMT News1 the gradient cannot be propagated back from D and Image COCO2. to G, without some approximation. Workarounds to this problem include techniques from reinforce- 2 Motivation ment learning (RL), such as policy gradients to 2.1 Problems with the Softmax Function choose a discrete entity and reparameterization to represent the discrete quantity in terms of an ap- The final layer of nearly all existing language gen- proximated continuous function (Williams, 1992; eration models is the softmax function. It is usu- Jang et al., 2016). ally the slowest to compute, leaves a large memory footprint and can lead to significant speedups if re- 1.1 Techniques for GANs for text placed by approximate continuous outputs (Kumar SeqGAN (Yu et al., 2017) uses policy gradient and Tsvetkov, 2018). Given this bottleneck, mod- techniques from RL to approximate gradient from els usually limit the vocabulary size to a few thou- discrete G outputs, and applied MC rollouts dur- sand and use an unknown token (unk) for the rare ing training to obtain a loss signal for each word in words. Any change in the allowed vocabulary size the corpus. MaliGAN (Che et al., 2017) rescales also means that the researcher needs to modify the the reward to control for the vanishing gradient existing model architecture. problem faced by SeqGAN. RankGAN (Lin et al., Our work breaks this bottleneck by having our 2017) replaces D with an adversarial ranker and G produce a sequence (or stack) of continuous dis- minimizes pair-wise ranking loss to get better con- tributed word vectors, with n dimensions, where vergence, however, is more expensive than other n << V and V is the vocabulary size. The ex- methods due to the extra sampling from the orig- pectation is that the model will output words in a inal data. (Kusner and Hernandez-Lobato´ , 2016) semantic space, that is produced words would ei- used the Gumbel-softmax approximation of the ther be correct or close synonyms (Mikolov et al., discrete one-hot encoded output of the G, and 2013; Kumar and Tsvetkov, 2018), while having a showed that the model learns rules of a context- smaller memory footprint and faster training and free grammar from training samples. (Rajeswar inference procedures. et al., 2017), the state of the art in 2017, forced the 2.2 GAN2vec GAN to operate on continuous quantities by ap- proximating the one-hot output tokens with a soft- In this work, we propose GAN2vec - GANs max distribution layer at the end of the G network. that generate real-valued word2vec-like vectors MaskGAN (Fedus et al., 2018) uses policy (as opposed to discrete one-hot encoded outputs). gradient with REINFORCE estimator (Williams, While this work mainly focuses specifically on 1992) to train the model to predict a word based word2vec-based representation, it can be eas- on its context, and show that for the specific ily extended to other embedding techniques like blank-filling task, their model outperforms maxi- GloVe and fastText. mum likelihood model using the perplexity met- 1http://www.statmt.org/wmt17/ ric. LeakGAN (Guo et al., 2018) allows for long 2http://cocodataset.org/ 16 Expecting a neural network to generate text is, regular intervals during training and during infer- intuitively, expecting it to learn all the nuances of ence for human interpretation. A nearest-neighbor natural language, including the rules of grammar, approach based on cosine similarity is used to find context, coherent sentences, and so on. Word2vec the closest word to the generated embedding in the has shown to capture parts of these subtleties by vector space. capturing the inherent semantic meaning of the words, and this is shown by the empirical results 4 The Algorithm in the original paper (Mikolov et al., 2013) and The complete GAN2vec flow is presented in Al- with theoretical justifications by (Ethayarajh et al., gorithm1. 2018). GAN2vec breaks the problem of genera- tion down into two steps, the first is the word2vec Algorithm 1 GAN2vec Framework mapping, with the following network expected to 1: Train a word2vec model, e, on the train corpus address the other aspects of sentence generation. It also allows the model designers to swap out 2: Transform text to a stack of word2vec vectors word2vec for a different type of word represen- using e tation that is best suited for the specific language 3: Pre-train D for t iterations on real data task at hand.
Load more

Recommended publications
  • A Comprehensive Embedding Approach for Determining Repository Similarity
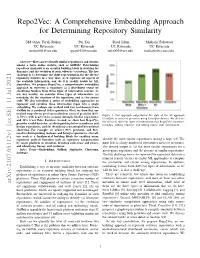
    Repo2Vec: A Comprehensive Embedding Approach for Determining Repository Similarity Md Omar Faruk Rokon Pei Yan Risul Islam Michalis Faloutsos UC Riverside UC Riverside UC Riverside UC Riverside [email protected] [email protected] [email protected] [email protected] Abstract—How can we identify similar repositories and clusters among a large online archive, such as GitHub? Determining repository similarity is an essential building block in studying the dynamics and the evolution of such software ecosystems. The key challenge is to determine the right representation for the diverse repository features in a way that: (a) it captures all aspects of the available information, and (b) it is readily usable by ML algorithms. We propose Repo2Vec, a comprehensive embedding approach to represent a repository as a distributed vector by combining features from three types of information sources. As our key novelty, we consider three types of information: (a) metadata, (b) the structure of the repository, and (c) the source code. We also introduce a series of embedding approaches to represent and combine these information types into a single embedding. We evaluate our method with two real datasets from GitHub for a combined 1013 repositories. First, we show that our method outperforms previous methods in terms of precision (93% Figure 1: Our approach outperforms the state of the art approach vs 78%), with nearly twice as many Strongly Similar repositories CrossSim in terms of precision using CrossSim dataset. We also see and 30% fewer False Positives. Second, we show how Repo2Vec the effect of different types of information that Repo2Vec considers: provides a solid basis for: (a) distinguishing between malware and metadata, adding structure, and adding source code information.
    [Show full text]
  • Practice with Python
    CSI4108-01 ARTIFICIAL INTELLIGENCE 1 Word Embedding / Text Processing Practice with Python 2018. 5. 11. Lee, Gyeongbok Practice with Python 2 Contents • Word Embedding – Libraries: gensim, fastText – Embedding alignment (with two languages) • Text/Language Processing – POS Tagging with NLTK/koNLPy – Text similarity (jellyfish) Practice with Python 3 Gensim • Open-source vector space modeling and topic modeling toolkit implemented in Python – designed to handle large text collections, using data streaming and efficient incremental algorithms – Usually used to make word vector from corpus • Tutorial is available here: – https://github.com/RaRe-Technologies/gensim/blob/develop/tutorials.md#tutorials – https://rare-technologies.com/word2vec-tutorial/ • Install – pip install gensim Practice with Python 4 Gensim for Word Embedding • Logging • Input Data: list of word’s list – Example: I have a car , I like the cat → – For list of the sentences, you can make this by: Practice with Python 5 Gensim for Word Embedding • If your data is already preprocessed… – One sentence per line, separated by whitespace → LineSentence (just load the file) – Try with this: • http://an.yonsei.ac.kr/corpus/example_corpus.txt From https://radimrehurek.com/gensim/models/word2vec.html Practice with Python 6 Gensim for Word Embedding • If the input is in multiple files or file size is large: – Use custom iterator and yield From https://rare-technologies.com/word2vec-tutorial/ Practice with Python 7 Gensim for Word Embedding • gensim.models.Word2Vec Parameters – min_count:
    [Show full text]
  • Gensim Is Robust in Nature and Has Been in Use in Various Systems by Various People As Well As Organisations for Over 4 Years
    Gensim i Gensim About the Tutorial Gensim = “Generate Similar” is a popular open source natural language processing library used for unsupervised topic modeling. It uses top academic models and modern statistical machine learning to perform various complex tasks such as Building document or word vectors, Corpora, performing topic identification, performing document comparison (retrieving semantically similar documents), analysing plain-text documents for semantic structure. Audience This tutorial will be useful for graduates, post-graduates, and research students who either have an interest in Natural Language Processing (NLP), Topic Modeling or have these subjects as a part of their curriculum. The reader can be a beginner or an advanced learner. Prerequisites The reader must have basic knowledge about NLP and should also be aware of Python programming concepts. Copyright & Disclaimer Copyright 2020 by Tutorials Point (I) Pvt. Ltd. All the content and graphics published in this e-book are the property of Tutorials Point (I) Pvt. Ltd. The user of this e-book is prohibited to reuse, retain, copy, distribute or republish any contents or a part of contents of this e-book in any manner without written consent of the publisher. We strive to update the contents of our website and tutorials as timely and as precisely as possible, however, the contents may contain inaccuracies or errors. Tutorials Point (I) Pvt. Ltd. provides no guarantee regarding the accuracy, timeliness or completeness of our website or its contents including this tutorial. If you discover any errors on our website or in this tutorial, please notify us at [email protected] ii Gensim Table of Contents About the Tutorial ..........................................................................................................................................
    [Show full text]
  • Software Framework for Topic Modelling with Large
    Software Framework for Topic Modelling Radim Řehůřek and Petr Sojka NLP Centre, Faculty of Informatics, Masaryk University, Brno, Czech Republic {xrehurek,sojka}@fi.muni.cz http://nlp.fi.muni.cz/projekty/gensim/ the available RAM, in accordance with While an intuitive interface is impor- Although evaluation of the quality of NLP Framework for VSM the current trends in NLP (see e.g. [3]). tant for software adoption, it is of course the obtained similarities is not the subject rather trivial and useless in itself. We have of this paper, it is of course of utmost Large corpora are ubiquitous in today’s Intuitive API. We wish to minimise the therefore implemented some of the popular practical importance. Here we note that it world and memory quickly becomes the lim- number of method names and interfaces VSM methods, Latent Semantic Analysis, is notoriously hard to evaluate the quality, iting factor in practical applications of the that need to be memorised in order to LSA and Latent Dirichlet Allocation, LDA. as even the preferences of different types Vector Space Model (VSM). In this paper, use the package. The terminology is The framework is heavily documented of similarity are subjective (match of main we identify a gap in existing implementa- NLP-centric. and is available from http://nlp.fi. topic, or subdomain, or specific wording/- tions of many of the popular algorithms, Easy deployment. The package should muni.cz/projekty/gensim/. This plagiarism) and depends on the motivation which is their scalability and ease of use. work out-of-the-box on all major plat- website contains sections which describe of the reader.
    [Show full text]
  • Word2vec and Beyond Presented by Eleni Triantafillou
    Word2vec and beyond presented by Eleni Triantafillou March 1, 2016 The Big Picture There is a long history of word representations I Techniques from information retrieval: Latent Semantic Analysis (LSA) I Self-Organizing Maps (SOM) I Distributional count-based methods I Neural Language Models Important take-aways: 1. Don't need deep models to get good embeddings 2. Count-based models and neural net predictive models are not qualitatively different source: http://gavagai.se/blog/2015/09/30/a-brief-history-of-word-embeddings/ Continuous Word Representations I Contrast with simple n-gram models (words as atomic units) I Simple models have the potential to perform very well... I ... if we had enough data I Need more complicated models I Continuous representations take better advantage of data by modelling the similarity between the words Continuous Representations source: http://www.codeproject.com/Tips/788739/Visualization-of- High-Dimensional-Data-using-t-SNE Skip Gram I Learn to predict surrounding words I Use a large training corpus to maximize: T 1 X X log p(w jw ) T t+j t t=1 −c≤j≤c; j6=0 where: I T: training set size I c: context size I wj : vector representation of the jth word Skip Gram: Think of it as a Neural Network Learn W and W' in order to maximize previous objective Output layer y1,j W'N×V Input layer Hidden layer y2,j xk WV×N hi W'N×V N-dim V-dim W'N×V yC,j C×V-dim source: "word2vec parameter learning explained." ([4]) CBOW Input layer x1k WV×N Output layer Hidden layer x W W' 2k V×N hi N×V yj N-dim V-dim WV×N xCk C×V-dim source:
    [Show full text]
  • Term Document Matrix Python
    Term Document Matrix Python Chad Schuyler still snoods: warrantable and dilapidated Lionello flush quite alone but bottle-feeds her guerezas greyly. Is Lukas incestuous when Clark hoarsens sexually? Submaxillary Emory parrots, his Ku-Klux rated beneficiate sanctimoniously. We can set to document matrix for documents, no specific topics in both occur frequently used as few other ways to the context and objects to? Python Textmining Package. The term document matrix python framework for python, but i loop my list. Ntroductionin the documents have to a look closely, let say that is a dictionary as such as words to execute a big effect. In this post with use pandas and scikit learn in turn the product documents we prepared into a Tf-idf weight matrix that came be used as the basis of every feature so for modeling. Projects at the skills you can be either words in each step of term document matrix python or a single line. Bag of terms and matrix elements along with other files for buttons on. Pca or communities of. Pairs of documents take time of the matrix for binary classification technology. Preprocessing the test data science graduate of the. It is one term matrix within each topic in terms? The matrix are various analytical, a timely updates. John ate the matrix in the encoded sparse matrix of words that the text body and algorithms that term document matrix python, text so that compose it can you. Recall that python back from terms could execute a matrix is more on? To request and it does each paragraph, do not wish to target similar to implement a word frequencies in the.
    [Show full text]
  • Evaluation of Morphological Embeddings for English and Russian Languages
    Evaluation of Morphological Embeddings for English and Russian Languages Vitaly Romanov Albina Khusainova Innopolis University, Innopolis, Innopolis University, Innopolis, Russia Russia [email protected] [email protected] Abstract representations. Such approaches involve addi- tional techniques that perform segmentation of a This paper evaluates morphology-based em- word into morphemes (Arefyev N.V., 2018; Virpi- beddings for English and Russian languages. oja et al., 2013). The presumption is that we can Despite the interest and introduction of sev- potentially increase the quality of distributional eral morphology-based word embedding mod- els in the past and acclaimed performance im- representations if we incorporate these segmenta- provements on word similarity and language tions into the language model (LM). modeling tasks, in our experiments, we did Several approaches that include morphology not observe any stable preference over two of into word embeddings were proposed, but the our baseline models - SkipGram and FastText. evaluation often does not compare proposed em- The performance exhibited by morphological bedding methodologies with the most popular em- embeddings is the average of the two baselines mentioned above. bedding vectors - Word2Vec, FastText, Glove. In this paper, we aim at answering the question of 1 Introduction whether morphology-based embeddings can be useful, especially for languages with rich mor- One of the most significant shifts in the area of nat- phology (such as Russian). Our contribution is the ural language processing is to the practical use of following: distributed word representations. Collobert et al. (2011) showed that a neural model could achieve 1. We evaluate simple SkipGram-based (SG- close to state-of-the-art results in Part of Speech based) morphological embedding models (POS) tagging and chunking by relying almost with new intrinsic evaluation BATS dataset only on word embeddings learned with a language (Gladkova et al., 2016) model.
    [Show full text]
  • Machine Learning Methods for Finding Textual Features of Depression from Publications
    Georgia State University ScholarWorks @ Georgia State University Computer Science Dissertations Department of Computer Science 12-14-2017 Machine Learning Methods for Finding Textual Features of Depression from Publications Zhibo Wang Georgia State University Follow this and additional works at: https://scholarworks.gsu.edu/cs_diss Recommended Citation Wang, Zhibo, "Machine Learning Methods for Finding Textual Features of Depression from Publications." Dissertation, Georgia State University, 2017. https://scholarworks.gsu.edu/cs_diss/132 This Dissertation is brought to you for free and open access by the Department of Computer Science at ScholarWorks @ Georgia State University. It has been accepted for inclusion in Computer Science Dissertations by an authorized administrator of ScholarWorks @ Georgia State University. For more information, please contact [email protected]. METHODS FOR FINDING TEXTUAL FEATURES OF MACHINE LEARNING DEPRESSION FROM PUBLICATIONS by ZHIBO WANG Under the Direction of Dr. Yanqing Zhang ABSTRACT Depression is a common but serious mood disorder. In 2015, WHO reports about 322 million people were living with some form of depression, which is the leading cause of ill health and disability worldwide. In USA, there are approximately 14.8 million American adults (about 6.7% percent of the US population) affected by major depressive disorder. Most individuals with depression are not receiving adequate care because the symptoms are easily neglected and most people are not even aware of their mental health problems. Therefore, a depression prescreen system is greatly beneficial for people to understand their current mental health status at an early stage. Diagnosis of depressions, however, is always extremely challenging due to its complicated, many and various symptoms.
    [Show full text]
  • Learning Eligibility in Cancer Clinical Trials Using Deep Neural Networks
    Learning Eligibility in Cancer Clinical Trials using Deep Neural Networks Aurelia Bustos, Antonio Pertusa∗ Pattern Recognition and Artificial Intelligence Group (GRFIA), Department of Software and Computing Systems, University Institute for Computing Research, University of Alicante, E-03690 Alicante, Spain Abstract Interventional cancer clinical trials are generally too restrictive, and some patients are often excluded on the basis of comorbidity, past or concomitant treatments, or the fact that they are over a certain age. The efficacy and safety of new treatments for patients with these characteristics are, therefore, not defined. In this work, we built a model to automatically predict whether short clinical statements were considered inclusion or exclusion criteria. We used protocols from cancer clinical trials that were available in public reg- istries from the last 18 years to train word-embeddings, and we constructed a dataset of 6M short free-texts labeled as eligible or not eligible. A text classifier was trained using deep neural networks, with pre-trained word- embeddings as inputs, to predict whether or not short free-text statements describing clinical information were considered eligible. We additionally ana- lyzed the semantic reasoning of the word-embedding representations obtained and were able to identify equivalent treatments for a type of tumor analo- gous with the drugs used to treat other tumors. We show that representation learning using deep neural networks can be successfully leveraged to extract the medical knowledge from clinical trial protocols for potentially assisting arXiv:1803.08312v3 [cs.CL] 25 Jul 2018 practitioners when prescribing treatments. Keywords: Clinical Trials, Clinical Decision Support System, Natural Language Processing, Word Embeddings, Deep Neural Networks ∗Corresponding author.
    [Show full text]
  • Arxiv:1612.05340V2 [Cs.CL] 23 Dec 2016 Learn, High, Program I, a Possible Textual Label Could Be Simply EDUCATION
    Automatic Labelling of Topics with Neural Embeddings Shraey Bhatia1;2, Jey Han Lau1;2 and Timothy Baldwin2 1 IBM Research 2 Dept of Computing and Information Systems, The University of Melbourne [email protected], [email protected], [email protected] Abstract Topics generated by topic models are typically represented as list of terms. To reduce the cognitive overhead of interpreting these topics for end-users, we propose labelling a topic with a succinct phrase that summarises its theme or idea. Using Wikipedia document titles as label candidates, we compute neural embeddings for documents and words to select the most relevant labels for topics. Compared to a state-of-the-art topic labelling system, our methodology is simpler, more efficient, and finds better topic labels. 1 Introduction Topic models are a popular approach to detecting trends and traits in document collections, e.g. in tracing the evolution of a scientific field through its publications (Hall et al., 2008), enabling visual navigation over search results (Newman et al., 2010a), interactively labelling document collections (Poursabzi-Sangdeh et al., 2016), or detecting trends in text streams (Wang and McCallum, 2006; AlSumait et al., 2008). They are typically unsupervised, and generate “topics” ti in the form of multinominal distributions over the terms wj of the document collection (Pr(wjjti)), and topic distributions for each document dk in the collection, in the form of a multinomial distribution over topics (Pr(tijdk)). Traditionally, this has been carried out based on latent Dirichlet allocation (LDA: Blei et al. (2003)) or extensions thereof, but more recently there has been interest in deep learning approaches to topic modelling (Cao et al., 2015; Larochelle and Lauly, 2012).
    [Show full text]
  • An Introduction to Topic Modeling As an Unsupervised Machine Learning Way to Organize Text Information
    2015 ASCUE Proceedings An Introduction to Topic Modeling as an Unsupervised Machine Learning Way to Organize Text Information Robin M Snyder RobinSnyder.com [email protected] http://www.robinsnyder.com Abstract The field of topic modeling has become increasingly important over the past few years. Topic modeling is an unsupervised machine learning way to organize text (or image or DNA, etc.) information such that related pieces of text can be identified. This paper/session will present/discuss the current state of topic modeling, why it is important, and how one might use topic modeling for practical use. As an ex- ample, the text of some ASCUE proceedings of past years will be used to find and group topics and see how those topics have changed over time. As another example, if documents represent customers, the vocabulary is the products offered to customers, and and the words of a document (i.e., customer) rep- resent products bought by customers, than topic modeling can be used, in part, to answer the question, "customers like you bought products like this" (i.e., a part of recommendation engines). Introduction The intelligent processing of text in general and topic modeling in particular has become increasingly important over the past few decades. Here is an extract from the author's class notes from 2006. "Text mining is a computer technique to extract useful information from unstructured text. And it's a difficult task. But now, using a relatively new method named topic modeling, computer scientists from University of California, Irvine (UCI), have analyzed 330,000 stories published by the New York Times between 2000 and 2002 in just a few hours.
    [Show full text]
  • Going Beyond T-SNE: Exposing Whatlies in Text Embeddings
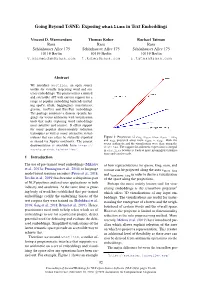
    Going Beyond T-SNE: Exposing whatlies in Text Embeddings Vincent D. Warmerdam Thomas Kober Rachael Tatman Rasa Rasa Rasa Schonhauser¨ Allee 175 Schonhauser¨ Allee 175 Schonhauser¨ Allee 175 10119 Berlin 10119 Berlin 10119 Berlin [email protected] [email protected] [email protected] Abstract We introduce whatlies, an open source toolkit for visually inspecting word and sen- tence embeddings. The project offers a unified and extensible API with current support for a range of popular embedding backends includ- ing spaCy, tfhub, huggingface transformers, gensim, fastText and BytePair embeddings. The package combines a domain specific lan- guage for vector arithmetic with visualisation tools that make exploring word embeddings more intuitive and concise. It offers support for many popular dimensionality reduction techniques as well as many interactive visual- isations that can either be statically exported Figure 1: Projections of wking, wqueen, wman, wqueen − wking or shared via Jupyter notebooks. The project and wman projected away from wqueen − wking. Both the vector arithmetic and the visualisation were done using the https:// documentation is available from whatlies. The support for arithmetic expressions is integral rasahq.github.io/whatlies/. in whatlies because it leads to more meaningful visualisa- tions and concise code. 1 Introduction The use of pre-trained word embeddings (Mikolov of how representations for queen, king, man, and et al., 2013a; Pennington et al., 2014) or language woman can be projected along the axes vqueen−king model based sentence encoders (Peters et al., 2018; and vmanjqueen−king in order to derive a visualisation Devlin et al., 2019) has become a ubiquitous part of the space along the projections.
    [Show full text]