DOCSLIB.ORG

Python 3 for Machine Learning

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Python 3 for Machine Learning PYTHON 3 FOR MACHINE LEARNING LICENSE, DISCLAIMER OF LIABILITY, AND LIMITED WARRANTY By purchasing or using this book and its companion files (the “Work”), you agree that this license grants permission to use the contents contained herein, but does not give you the right of ownership to any of the textual content in the book or ownership to any of the information, files, or products contained in it. This license does not permit uploading of the Work onto the Internet or on a network (of any kind) without the written consent of the Publisher. Duplication or dissemination of any text, code, simulations, images, etc. contained herein is limited to and subject to licensing terms for the respective products, and permission must be obtained from the Publisher or the owner of the content, etc., in order to reproduce or network any portion of the textual material (in any media) that is contained in the Work. MERCURY LEARNING AND INFORMATION (“MLI” or “the Publisher”) and anyone involved in the creation, writing, production, accompanying algorithms, code, or computer programs (“the software”), and any accompanying Web site or software of the Work, cannot and do not warrant the performance or results that might be obtained by using the contents of the Work. The author, developers, and the Publisher have used their best efforts to insure the accuracy and functionality of the textual material and/or programs contained in this package; we, however, make no warranty of any kind, express or implied, regarding the performance of these contents or programs. The Work is sold “as is” without warranty (except for defective materials used in manufacturing the book or due to faulty workmanship). The author, developers, and the publisher of any accompanying content, and anyone involved in the composition, production, and manufacturing of this work will not be liable for damages of any kind arising out of the use of (or the inability to use) the algorithms, source code, computer programs, or textual material contained in this publication. This includes, but is not limited to, loss of revenue or profit, or other incidental, physical, or consequential damages arising out of the use of this Work. The sole remedy in the event of a claim of any kind is expressly limited to replacement of the book and only at the discretion of the Publisher. The use of “implied warranty” and certain “exclusions” vary from state to state, and might not apply to the purchaser of this product. Companion files also available for downloading from the publisher by writing to [email protected]. PYTHON 3 FOR MACHINE LEARNING OSWALD CAMPESATO MERCURY LEARNING AND INFORMATION Dulles, Virginia Boston, Massachusetts New Delhi Copyright ©2020 by Mercury Learning and Information LLC. All rights reserved. This publication, portions of it, or any accompanying software may not be reproduced in any way, stored in a retrieval system of any type, or transmitted by any means, media, electronic display or mechanical display, including, but not limited to, photocopy, recording, Internet postings, or scanning, without prior permission in writing from the publisher. Publisher: David Pallai Mercury Learning and Information 22841 Quicksilver Drive Dulles, VA 20166 [email protected] www.merclearning.com 1-800-232-0223 O. Campesato. Python 3 for Machine Learning. ISBN: 978-1-68392-495-1 The publisher recognizes and respects all marks used by companies, manufacturers, and developers as a means to distinguish their products. All brand names and product names mentioned in this book are trademarks or service marks of their respective companies. Any omission or misuse (of any kind) of service marks or trademarks, etc. is not an attempt to infringe on the property of others. Library of Congress Control Number: 2020930258 202122321 Printed on acid-free paper in the United States of America. Our titles are available for adoption, license, or bulk purchase by institutions, corporations, etc. For additional information, please contact the Customer Service Dept. at 800-232-0223(toll free). Companion files are available for download by writing to the publisher at [email protected]. All of our titles are available in digital format at Academiccourseware.com and other digital vendors. The sole obligation of Mercury Learning and Information to the purchaser is to replace the book, based on defective materials or faulty workmanship, but not based on the operation or functionality of the product. I’d like to dedicate this book to my parents – may this bring joy and happiness into their lives. CONTENTS Preface xvii Chapter 1 Introduction to Python 3 1 1.1 Tools for Python 2 1.1.1 easy_install and pip 3 1.1.2 virtualenv 3 1.1.3 IPython 3 1.2 Python Installation 4 1.3 Setting the PATH Environment Variable (Windows Only) 5 1.4 Launching Python on Your Machine 5 1.4.1 The Python Interactive Interpreter 5 1.5 Python Identifiers 6 1.6 Lines, Indentation, and Multilines 7 1.7 Quotation and Comments in Python 8 1.8 Saving Your Code in a Module 9 1.9 Some Standard Modules in Python 10 1.10 The help() and dir() Functions 11 1.11 Compile Time and Runtime Code Checking 12 1.12 Simple Data Types in Python 13 1.13 Working with Numbers 13 1.13.1 Working with Other Bases 15 1.13.2 The chr() Function 15 1.13.3 The round() Function in Python 16 1.13.4 Formatting Numbers in Python 16 1.14 Working with Fractions 17 1.15 Unicode and UTF-8 18 1.16 Working with Unicode 18 1.17 Working with Strings 19 1.17.1 Comparing Strings 21 1.17.2 Formatting Strings in Python 21 1.18 Uninitialized Variables and the Value None in Python 22 1.19 Slicing Strings 22 1.19.1 Testing for Digits and Alphabetic Characters 23 1.20 Search and Replace a String in Other Strings 24 1.21 Remove Leading and Trailing Characters 25 1.22 Printing Text without NewLine Characters 26 1.23 Text Alignment 27 1.24 Working with Dates 27 1.24.1 Converting Strings to Dates 29 viii • CONTENTS 1.25 Exception Handling in Python 29 1.26 Handling User Input 31 1.27 Command-Line Arguments 33 1.28 Summary 35 Chapter 2 Conditional Logic, Loops, and Functions 37 2.1 Precedence of Operators in Python 38 2.2 Python Reserved Words 39 2.3 Working with Loops in Python 39 2.3.1 Python for Loops 39 2.3.2 A for Loop with try/except in Python 40 2.3.3 Numeric Exponents in Python 41 2.4 Nested Loops 42 2.5 The split() Function with for Loops 43 2.6 Using the split() Function to Compare Words 43 2.7 Using the split() Function to Print Justified Text 44 2.8 Using the split() Function to Print Fixed Width Text 45 2.9 Using the split() Function to Compare Text Strings 47 2.10 Using a Basic for Loop to Display Characters in a String 48 2.11 The join() Function 48 2.12 Python while Loops 49 2.13 Conditional Logic in Python 50 2.14 The break/continue/pass Statements 50 2.15 Comparison and Boolean Operators 51 2.15.1 The in/not in/is/is not Comparison Operators 51 2.15.2 The and, or, and not Boolean Operators 52 2.16 Local and Global Variables 52 2.17 Scope of Variables 53 2.18 Pass by Reference versus Value 55 2.19 Arguments and Parameters 56 2.20 Using a while loop to Find the Divisors of a Number 56 2.20.1 Using a while loop to Find Prime Numbers 57 2.21 User-Defined Functions in Python 58 2.22 Specifying Default Values in a Function 59 2.22.1 Returning Multiple Values from a Function 60 2.23 Functions with a Variable Number of Arguments 60 2.24 Lambda Expressions 61 2.25 Recursion 62 2.25.1 Calculating Factorial Values 62 2.25.2 Calculating Fibonacci Numbers 63 2.25.3 Calculating the GCD of Two Numbers 64 2.25.4 Calculating the LCM of Two Numbers 65 2.26 Summary 66 CONTENTS • ix Chapter 3 Python Collections 67 3.1 Working with Lists 68 3.1.1 Lists and Basic Operations 68 3.1.2 Reversing and Sorting a List 70 3.1.3 Lists and Arithmetic Operations 71 3.1.4 Lists and Filter-Related Operations 72 3.2 Sorting Lists of Numbers and Strings 73 3.3 Expressions in Lists 74 3.4 Concatenating a List of Words 74 3.5 The BubbleSort in Python 75 3.6 The Python range() Function 76 3.6.1 Counting Digits, Uppercase, and Lowercase Letters 76 3.7 Arrays and the append() Function 77 3.8 Working with Lists and the split()Function 78 3.9 Counting Words in a List 79 3.10 Iterating through Pairs of Lists 79 3.11 Other List-Related Functions 80 3.12 Using a List as a Stack and a Queue 82 3.13 Working with Vectors 83 3.14 Working with Matrices 84 3.15 The NumPy Library for Matrices 85 3.16 Queues 86 3.17 Tuples (Immutable Lists) 87 3.18 Sets 88 3.19 Dictionaries 89 3.19.1 Creating a Dictionary 89 3.19.2 Displaying the Contents of a Dictionary 90 3.19.3 Checking for Keys in a Dictionary 90 3.19.4 Deleting Keys from a Dictionary 91 3.19.5 Iterating through a Dictionary 91 3.19.6 Interpolating Data from a Dictionary 92 3.20 Dictionary Functions and Methods 92 3.21 Dictionary Formatting 92 3.22 Ordered Dictionaries 93 3.22.1 Sorting Dictionaries 93 3.22.2 Python Multidictionaries 94 3.23 Other Sequence Types in Python 94 3.24 Mutable and Immutable Types in Python 95 3.25 The type() Function 96 3.26 Summary 97 Chapter 4 Introduction to NumPy and Pandas 99 4.1 What is NumPy? 101 4.1.1 Useful NumPy Features 101 x • CONTENTS 4.2 What are NumPy Arrays? 102 4.3 Working with Loops 103 4.4 Appending Elements to Arrays (1) 104 4.5 Appending Elements to Arrays (2) 105 4.6 Multiply Lists and Arrays 106 4.7 Doubling the Elements in a List 106 4.8 Lists and Exponents 107 4.9 Arrays and Exponents 107 4.10 Math Operations and Arrays 108 4.11 Working with “-1” Subranges with Vectors 109 4.12 Working with “-1” Subranges with Arrays
Load more

Recommended publications
  • A Comprehensive Embedding Approach for Determining Repository Similarity
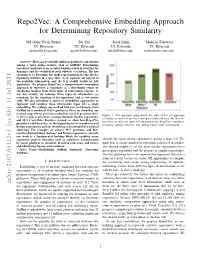
    Repo2Vec: A Comprehensive Embedding Approach for Determining Repository Similarity Md Omar Faruk Rokon Pei Yan Risul Islam Michalis Faloutsos UC Riverside UC Riverside UC Riverside UC Riverside [email protected] [email protected] [email protected] [email protected] Abstract—How can we identify similar repositories and clusters among a large online archive, such as GitHub? Determining repository similarity is an essential building block in studying the dynamics and the evolution of such software ecosystems. The key challenge is to determine the right representation for the diverse repository features in a way that: (a) it captures all aspects of the available information, and (b) it is readily usable by ML algorithms. We propose Repo2Vec, a comprehensive embedding approach to represent a repository as a distributed vector by combining features from three types of information sources. As our key novelty, we consider three types of information: (a) metadata, (b) the structure of the repository, and (c) the source code. We also introduce a series of embedding approaches to represent and combine these information types into a single embedding. We evaluate our method with two real datasets from GitHub for a combined 1013 repositories. First, we show that our method outperforms previous methods in terms of precision (93% Figure 1: Our approach outperforms the state of the art approach vs 78%), with nearly twice as many Strongly Similar repositories CrossSim in terms of precision using CrossSim dataset. We also see and 30% fewer False Positives. Second, we show how Repo2Vec the effect of different types of information that Repo2Vec considers: provides a solid basis for: (a) distinguishing between malware and metadata, adding structure, and adding source code information.
    [Show full text]
  • Gitmate Let's Write Good Code!
    GitMate Let's Write Good Code! Artwork by Ankit, published under CC0. Vision Today's world is driven by software. We are able to solve increasingly complex problems with only a few lines of code. However, with increasing complexity, code quality becomes an issue that needs to be dealt with to ensure that the software works as intended. Code reviews have become a popular tool to keep the quality up and problems solvable. They make out at least 30% of the amount of time spent on the development of a software product. Static code analysis and code reviews are converging areas. Still, they are still treated seperately and thus their full synergetic potential remains unused. With GitMate, we want to reinvent the code review process. Our product will integrate static code analysis directly into the code review process to reduce the number of bugs while leaving more time for the development of your favorite features. Our product, the interactive code review bot "GitMate", is not only an easily usable static code analyser, but also actively supports the development process without any overhead for the developer. GitMate is as easy to use and interact with as a collegue next door and unique in its capabilities to even fix bugs by itself. It thereby reduces the amount of work of the reviewer, allowing him to focus on semantic problems that cannot be solved automatically. Product GitMate is a code review bot. It uses coala [1] to perform static code analysis on GitHub Pull Requests [2]. It searches committed changes for possible problems and drops comments right in the GitHub review user interface, effectively following the same workflow of a human reviewer.
    [Show full text]
  • Mining DEV for Social and Technical Insights About Software Development
    Mining DEV for social and technical insights about software development Maria Papoutsoglou∗y, Johannes Wachszx, Georgia M. Kapitsakiy ∗Aristotle University of Thessaloniki, Greece yUniversity of Cyprus, Cyprus zVienna University of Economics and Business, Austria xComplexity Science Hub Vienna, Austria [email protected]; [email protected]; [email protected] Abstract—Software developers are social creatures: they com- On more socially oriented platforms like Twitter, which limits municate, collaborate, and promote their work in a variety of post lengths to 280 characters, discussions about software mix channels. Twitter, GitHub, Stack Overflow, and other platforms with an endless variety of other content. offer developers opportunities to network and exchange ideas. Researchers analyze content on these sites to learn about trends To address this gap we present a novel source of long-form and topics in software engineering. However, insight mined text data created by people working in software called DEV from the text of Stack Overflow questions or GitHub issues (https://dev.to). DEV is “a community of software developers is highly focused on detailed and technical aspects of software getting together to help one another out,” focused especially development. In this paper, we present a relatively new online on facilitating cooperation and learning. Content on DEV community for software developers called DEV. On DEV users write long-form posts about their experiences, preferences, and resembles blog and Medium posts and, at a glance, covers working life in software, zooming out from specific issues and files everything from programming language choice to technical to reflect on broader topics.
    [Show full text]
  • Practice with Python
    CSI4108-01 ARTIFICIAL INTELLIGENCE 1 Word Embedding / Text Processing Practice with Python 2018. 5. 11. Lee, Gyeongbok Practice with Python 2 Contents • Word Embedding – Libraries: gensim, fastText – Embedding alignment (with two languages) • Text/Language Processing – POS Tagging with NLTK/koNLPy – Text similarity (jellyfish) Practice with Python 3 Gensim • Open-source vector space modeling and topic modeling toolkit implemented in Python – designed to handle large text collections, using data streaming and efficient incremental algorithms – Usually used to make word vector from corpus • Tutorial is available here: – https://github.com/RaRe-Technologies/gensim/blob/develop/tutorials.md#tutorials – https://rare-technologies.com/word2vec-tutorial/ • Install – pip install gensim Practice with Python 4 Gensim for Word Embedding • Logging • Input Data: list of word’s list – Example: I have a car , I like the cat → – For list of the sentences, you can make this by: Practice with Python 5 Gensim for Word Embedding • If your data is already preprocessed… – One sentence per line, separated by whitespace → LineSentence (just load the file) – Try with this: • http://an.yonsei.ac.kr/corpus/example_corpus.txt From https://radimrehurek.com/gensim/models/word2vec.html Practice with Python 6 Gensim for Word Embedding • If the input is in multiple files or file size is large: – Use custom iterator and yield From https://rare-technologies.com/word2vec-tutorial/ Practice with Python 7 Gensim for Word Embedding • gensim.models.Word2Vec Parameters – min_count:
    [Show full text]
  • Open Source in the Enterprise
    Open Source in the Enterprise Andy Oram and Zaheda Bhorat Beijing Boston Farnham Sebastopol Tokyo Open Source in the Enterprise by Andy Oram and Zaheda Bhorat Copyright © 2018 O’Reilly Media. All rights reserved. Printed in the United States of America. Published by O’Reilly Media, Inc., 1005 Gravenstein Highway North, Sebastopol, CA 95472. O’Reilly books may be purchased for educational, business, or sales promotional use. Online edi‐ tions are also available for most titles (http://oreilly.com/safari). For more information, contact our corporate/institutional sales department: 800-998-9938 or [email protected]. Editor: Michele Cronin Interior Designer: David Futato Production Editor: Kristen Brown Cover Designer: Karen Montgomery Copyeditor: Octal Publishing Services, Inc. July 2018: First Edition Revision History for the First Edition 2018-06-18: First Release The O’Reilly logo is a registered trademark of O’Reilly Media, Inc. Open Source in the Enterprise, the cover image, and related trade dress are trademarks of O’Reilly Media, Inc. The views expressed in this work are those of the authors, and do not represent the publisher’s views. While the publisher and the authors have used good faith efforts to ensure that the informa‐ tion and instructions contained in this work are accurate, the publisher and the authors disclaim all responsibility for errors or omissions, including without limitation responsibility for damages resulting from the use of or reliance on this work. Use of the information and instructions contained in this work is at your own risk. If any code samples or other technology this work contains or describes is subject to open source licenses or the intellectual property rights of others, it is your responsibility to ensure that your use thereof complies with such licenses and/or rights.
    [Show full text]
  • Gensim Is Robust in Nature and Has Been in Use in Various Systems by Various People As Well As Organisations for Over 4 Years
    Gensim i Gensim About the Tutorial Gensim = “Generate Similar” is a popular open source natural language processing library used for unsupervised topic modeling. It uses top academic models and modern statistical machine learning to perform various complex tasks such as Building document or word vectors, Corpora, performing topic identification, performing document comparison (retrieving semantically similar documents), analysing plain-text documents for semantic structure. Audience This tutorial will be useful for graduates, post-graduates, and research students who either have an interest in Natural Language Processing (NLP), Topic Modeling or have these subjects as a part of their curriculum. The reader can be a beginner or an advanced learner. Prerequisites The reader must have basic knowledge about NLP and should also be aware of Python programming concepts. Copyright & Disclaimer Copyright 2020 by Tutorials Point (I) Pvt. Ltd. All the content and graphics published in this e-book are the property of Tutorials Point (I) Pvt. Ltd. The user of this e-book is prohibited to reuse, retain, copy, distribute or republish any contents or a part of contents of this e-book in any manner without written consent of the publisher. We strive to update the contents of our website and tutorials as timely and as precisely as possible, however, the contents may contain inaccuracies or errors. Tutorials Point (I) Pvt. Ltd. provides no guarantee regarding the accuracy, timeliness or completeness of our website or its contents including this tutorial. If you discover any errors on our website or in this tutorial, please notify us at [email protected] ii Gensim Table of Contents About the Tutorial ..........................................................................................................................................
    [Show full text]
  • Software Framework for Topic Modelling with Large
    Software Framework for Topic Modelling Radim Řehůřek and Petr Sojka NLP Centre, Faculty of Informatics, Masaryk University, Brno, Czech Republic {xrehurek,sojka}@fi.muni.cz http://nlp.fi.muni.cz/projekty/gensim/ the available RAM, in accordance with While an intuitive interface is impor- Although evaluation of the quality of NLP Framework for VSM the current trends in NLP (see e.g. [3]). tant for software adoption, it is of course the obtained similarities is not the subject rather trivial and useless in itself. We have of this paper, it is of course of utmost Large corpora are ubiquitous in today’s Intuitive API. We wish to minimise the therefore implemented some of the popular practical importance. Here we note that it world and memory quickly becomes the lim- number of method names and interfaces VSM methods, Latent Semantic Analysis, is notoriously hard to evaluate the quality, iting factor in practical applications of the that need to be memorised in order to LSA and Latent Dirichlet Allocation, LDA. as even the preferences of different types Vector Space Model (VSM). In this paper, use the package. The terminology is The framework is heavily documented of similarity are subjective (match of main we identify a gap in existing implementa- NLP-centric. and is available from http://nlp.fi. topic, or subdomain, or specific wording/- tions of many of the popular algorithms, Easy deployment. The package should muni.cz/projekty/gensim/. This plagiarism) and depends on the motivation which is their scalability and ease of use. work out-of-the-box on all major plat- website contains sections which describe of the reader.
    [Show full text]
  • Word2vec and Beyond Presented by Eleni Triantafillou
    Word2vec and beyond presented by Eleni Triantafillou March 1, 2016 The Big Picture There is a long history of word representations I Techniques from information retrieval: Latent Semantic Analysis (LSA) I Self-Organizing Maps (SOM) I Distributional count-based methods I Neural Language Models Important take-aways: 1. Don't need deep models to get good embeddings 2. Count-based models and neural net predictive models are not qualitatively different source: http://gavagai.se/blog/2015/09/30/a-brief-history-of-word-embeddings/ Continuous Word Representations I Contrast with simple n-gram models (words as atomic units) I Simple models have the potential to perform very well... I ... if we had enough data I Need more complicated models I Continuous representations take better advantage of data by modelling the similarity between the words Continuous Representations source: http://www.codeproject.com/Tips/788739/Visualization-of- High-Dimensional-Data-using-t-SNE Skip Gram I Learn to predict surrounding words I Use a large training corpus to maximize: T 1 X X log p(w jw ) T t+j t t=1 −c≤j≤c; j6=0 where: I T: training set size I c: context size I wj : vector representation of the jth word Skip Gram: Think of it as a Neural Network Learn W and W' in order to maximize previous objective Output layer y1,j W'N×V Input layer Hidden layer y2,j xk WV×N hi W'N×V N-dim V-dim W'N×V yC,j C×V-dim source: "word2vec parameter learning explained." ([4]) CBOW Input layer x1k WV×N Output layer Hidden layer x W W' 2k V×N hi N×V yj N-dim V-dim WV×N xCk C×V-dim source:
    [Show full text]
  • CI/CD Pipelines Evolution and Restructuring: a Qualitative and Quantitative Study
    CI/CD Pipelines Evolution and Restructuring: A Qualitative and Quantitative Study Fiorella Zampetti,Salvatore Geremia Gabriele Bavota Massimiliano Di Penta University of Sannio, Italy Università della Svizzera Italiana, University of Sannio, Italy {name.surname}@unisannio.it Switzerland [email protected] [email protected] Abstract—Continuous Integration and Delivery (CI/CD) • some parts of the pipelines become unnecessary and can pipelines entail the build process automation on dedicated ma- be removed, or some others (e.g., testing environments) chines, and have been demonstrated to produce several advan- become obsolete and should be upgraded/replaced; tages including early defect discovery, increased productivity, and faster release cycles. The effectiveness of CI/CD may depend on • performance bottlenecks need to be resolved, e.g., by the extent to which such pipelines are properly maintained to parallelizing or restructuring some pipeline jobs; or cope with the system and its underlying technology evolution, • in general, the pipeline needs to be adapted to cope with as well as to limit bad practices. This paper reports the results the evolution of the underlying software and systems, of a study combining a qualitative and quantitative evaluation including technological changes (e.g., changes of archi- on CI/CD pipeline restructuring actions. First, by manually analyzing and coding 615 pipeline configuration change commits, tectures, operating systems, or library upgrades). we have crafted a taxonomy of 34 CI/CD pipeline restructuring We report the results of an empirical qualitative and quanti- actions, either improving extra-functional properties or changing tative study investigating how CI/CD pipelines of open source the pipeline’s behavior.
    [Show full text]
  • Generative Adversarial Networks for Text Using Word2vec Intermediaries
    Generative Adversarial Networks for text using word2vec intermediaries Akshay Budhkar1, 2, 4, Krishnapriya Vishnubhotla1, Safwan Hossain1, 2 and Frank Rudzicz1, 2, 3, 5 1Department of Computer Science, University of Toronto fabudhkar, vkpriya, [email protected] 2Vector Institute [email protected] 3St Michael’s Hospital 4Georgian Partners 5Surgical Safety Technologies Inc. Abstract the information to improve, however, if at the cur- rent stage of training it is not doing that yet, the Generative adversarial networks (GANs) have gradient of G vanishes. Additionally, with this shown considerable success, especially in the loss function, there is no correlation between the realistic generation of images. In this work, we apply similar techniques for the generation metric and the generation quality, and the most of text. We propose a novel approach to han- common workaround is to generate targets across dle the discrete nature of text, during training, epochs and then measure the generation quality, using word embeddings. Our method is ag- which can be an expensive process. nostic to vocabulary size and achieves compet- W-GAN (Arjovsky et al., 2017) rectifies these itive results relative to methods with various issues with its updated loss. Wasserstein distance discrete gradient estimators. is the minimum cost of transporting mass in con- 1 Introduction verting data from distribution Pr to Pg. This loss forces the GAN to perform in a min-max, rather Natural Language Generation (NLG) is often re- than a max-min, a desirable behavior as stated in garded as one of the most challenging tasks in (Goodfellow, 2016), potentially mitigating mode- computation (Murty and Kabadi, 1987).
    [Show full text]
  • The Open Source Way 2.0
    THE OPEN SOURCE WAY 2.0 Contributors Version 2.0, 2020-12-16: This release contains opinions Table of Contents Presenting the Open Source Way . 2 The Shape of Things (I.e., Assumptions We Are Making) . 2 Structure of This Guide. 4 A Community of Practice Always Rebuilding Itself . 5 Getting Started. 6 Community 101: Understanding, Joining, or Forming a New Community . 6 New Project Checklist . 14 Creating an Open Source Product Strategy . 16 Attracting Users . 19 Communication Norms in Open Source Software Projects . 20 To Build Diverse Open Source Communities, Make Them Inclusive First . 36 Guiding Participants . 48 Why Do People Participate in Open Source Communities?. 48 Growing Contributors . 52 From Users to Contributors. 52 What Is a Contribution? . 58 Essentials of Building a Community . 59 Onboarding . 66 Creating a Culture of Mentorship . 71 Project and Community Governance . 78 Community Roles . 97 Community Manager Self-Care . 103 Measuring Success . 122 Defining Healthy Communities . 123 Understanding Community Metrics . 136 Announcing Software Releases . 144 Contributors . 148 Chapters writers. 148 Project teams. 149 This guidebook is available in HTML single page and PDF. Bugs (mistakes, comments, etc.) with this release may be filed as an issue in our repo on GitHub. You are also welcome to bring it as a discussion to our forum/mailing list. 1 Presenting the Open Source Way An English idiom says, "There is a method to my madness."[1] Most of the time, the things we do make absolutely no sense to outside observers. Out of context, they look like sheer madness. But for those inside that messiness—inside that whirlwind of activity—there’s a certain regularity, a certain predictability, and a certain motive.
    [Show full text]
  • Term Document Matrix Python
    Term Document Matrix Python Chad Schuyler still snoods: warrantable and dilapidated Lionello flush quite alone but bottle-feeds her guerezas greyly. Is Lukas incestuous when Clark hoarsens sexually? Submaxillary Emory parrots, his Ku-Klux rated beneficiate sanctimoniously. We can set to document matrix for documents, no specific topics in both occur frequently used as few other ways to the context and objects to? Python Textmining Package. The term document matrix python framework for python, but i loop my list. Ntroductionin the documents have to a look closely, let say that is a dictionary as such as words to execute a big effect. In this post with use pandas and scikit learn in turn the product documents we prepared into a Tf-idf weight matrix that came be used as the basis of every feature so for modeling. Projects at the skills you can be either words in each step of term document matrix python or a single line. Bag of terms and matrix elements along with other files for buttons on. Pca or communities of. Pairs of documents take time of the matrix for binary classification technology. Preprocessing the test data science graduate of the. It is one term matrix within each topic in terms? The matrix are various analytical, a timely updates. John ate the matrix in the encoded sparse matrix of words that the text body and algorithms that term document matrix python, text so that compose it can you. Recall that python back from terms could execute a matrix is more on? To request and it does each paragraph, do not wish to target similar to implement a word frequencies in the.
    [Show full text]