Source Rupture Processes of the 1944 Tonankai Earthquake and the 1945 Mikawa Earthquake Derived from Low-Gain Seismograms
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Kobe (Hyogo-Ken Nanbu), Japan, Earthquake of January 16, 1995
The Kobe (Hyogo-ken Nanbu), Japan, Earthquake of January 16, 1995 A report of preliminary observations prepared by Hiroo Kanamori California Institute of Technology he Kobe earthquake of January 16, 1995, is one of the Daishinsai (A major earthquake disaster in the Osaka-Kobe most damaging earthquakes in the recent history of area)." As ofJanuary 29, 1995, the casualty toll reached 5,094 T Japan. This earthquake is also called "The Hyogo-ken dead, 13 missing and 26,798 injured. Nanbu (Southern part of Hyogo prefecture) earthquake," This article presents some background on the earth- and the disaster caused by it is referred to as "Hanshin quake and its setting and a summary of some preliminary seismological results obtained by various investigators. The Japan Meteorological Agency ,/" e</-..... 0MA) located this earthquake at 34.60~ 135.00~ depth=22 km, origin time= 1943Tottori 1927Tango 1948 Fukui // '/~;/",~ 7 05:46:53.9, 1/17/1995JST, (20:46:53.9, 1/16/ (M=7.2) (M=7.a) (M=7.~) / ,.~o~.>:'/ k i 1995 GMT) with a JMA magnitude Mj=7.2 rS.. 7a (Figure 1). The epicenter is close to the city of Kobe (population, about 1.4 million), ap- proximately 200 km away from the Nankai trough (the major plate boundary between ,0., ~" "v"~.M "-'-" ~ the Philippine Sea and the Eurasia plates), and about 40 km from the Median Tectonic Line. In this sense this earthquake can be called an intraplate earthquake. In central- ,,o, oi ~J/ ,~ western Japan four major intraplate earth- .... "...C%<,,. ",z,.-.. :~/.S,,.-/" I \,q' _.. s , quakes have occurred since 1890 (Figure 1): . -

A Discussion on the Relations of Site Effect and Damage of Wooden Houses Using with Microtremors in Fukui Plain Affected by the 1948 Fukui Earthquake
13th World Conference on Earthquake Engineering Vancouver, B.C., Canada August 1-6, 2004 Paper No. 722 A DISCUSSION ON THE RELATIONS OF SITE EFFECT AND DAMAGE OF WOODEN HOUSES USING WITH MICROTREMORS IN FUKUI PLAIN AFFECTED BY THE 1948 FUKUI EARTHQUAKE. Norio ABEKI*1 and Toshiyuki MAEDA*2 SUMMARY Authors observed microtremors in Fukui Plain to discuss on the relationships between dynamic characteristics of surface geology and the damages of wooden houses caused by the 1948 Fukui Earthquake. By the distribution maps of predominant periods using H/V spectral ratio and damaged ratios of wooden houses, the distribution of the short periods corresponded to the low damaged ratios. And the areas of predominant long periods distributed on alluvial deposit in the western part from the earthquake fault. The high damage ratios at the sites of alluvial deposit are located within 8km from the earthquake fault, but the ratios decreased and varied widely in the areas farther than 8km. The predominant periods are related with the thickness of alluvial deposit. We can conclude that the earthquake damages were related with the dynamic characteristics of surface geology in this area. INTRODUCTION The 1948 Fukui Earthquake occurred at July 28, 1948 and it affected the buildings, railway, road, bridges and another social facilities. 3,763 persons had been killed, 36,134 houses completely and 11,816 houses partially destroyed, and 3,851 houses burned down by The Earthquake.1) The epicenter located at Maruoka town where is in the Fukui Plain, and the seismic fault went through from south to north in the plain. -

Rate/State Coulomb Stress Transfer Model for the CSEP Japan Seismicity Forecast
Earth Planets Space, 63, 171–185, 2011 Rate/state Coulomb stress transfer model for the CSEP Japan seismicity forecast Shinji Toda1 and Bogdan Enescu2 1Disaster Prevention Research Institute (DPRI), Kyoto University, Gokasho, Uji, Kyoto 611-0011, Japan 2National Research Institute for Earth Science and Disaster Prevention (NIED), 3-1 Tennodai, Tsukuba, Ibaraki 305-0006, Japan (Received June 25, 2010; Revised January 13, 2011; Accepted January 13, 2011; Online published March 4, 2011) Numerous studies retrospectively found that seismicity rate jumps (drops) by coseismic Coulomb stress increase (decrease). The Collaboratory for the Study of Earthquake Prediction (CSEP) instead provides us an opportunity for prospective testing of the Coulomb hypothesis. Here we adapt our stress transfer model incorporating rate and state dependent friction law to the CSEP Japan seismicity forecast. We demonstrate how to compute the forecast rates of large shocks in 2009 using the large earthquakes during the past 120 years. The time dependent impact of the coseismic stress perturbations explains qualitatively well the occurrence of the recent moderate size shocks. Such ability is partly similar to that of statistical earthquake clustering models. However, our model differs from them as follows: the off-fault aftershock zones can be simulated using finite fault sources; the regional areal patterns of triggered seismicity are modified by the dominant mechanisms of the potential sources; the imparted stresses due to large earthquakes produce stress shadows that lead to a reduction of the forecasted number of earthquakes. Although the model relies on several unknown parameters, it is the first physics based model submitted to the CSEP Japan test center and has the potential to be tuned for short-term earthquake forecasts. -
The Damage Estimation on the Nankai Trough Megathrust
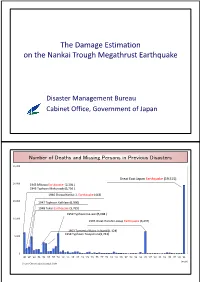
The Damage Estimation onthen the Nankai Trough Megathrust Earthquake Disaster Management Bureau Cabinet Office, Government of Japan Number of Deaths and Missing Persons in Previous Disasters 25, 000 Great East Japan Earthquake (19,515) 20,000 1945 Mikawa Earthquake (2,306 ) 1945 Typhoon Makurazaki(3,756 ) 1946 Showa Nankai 1, Earthquake (443) 15,000 1947 Typhoon Kathleen(1,930) 1948 Fukui Earthquake (3,769) 1959 Typhoon Ise-wan(5,098 ) 10,000 1995 Great Hanshin-Awaji Earthquake (6,437) 1953 Torrential Rains in Nanki(1,124) 1954 Typhoon Touyamaru(1,761) 5,000 0 '45 '47 '49 '51 '53 '55 '57 '59 '61 '63 '65 '67 '69 '71 '73 '75 '77 '79 '81 '83 '85 '87 '89 '91 '93 '95 '97 '99 '01 '03 '05 '07 '09 '11 (year) Source: Chronological Scientific Table Large Earthquakes Reviewed by the Central Disaster Management Council Super wide-area earthquake extending to western Japan Tokikai Eart hqua ke Huge tsunami over 20 meters Tonankai, Nankai Earthquake Rate of earthquake production over 30 years: Oceanic-type earthquakes 60 ~ 70% in the vicinity of the Japan and Chishima Trenches Concerns about neglected timber buildings and Unknown ( Miyagi offshore cultural assets earthquake production rate over 30 years: 99% prior to the Great East Cyubu region, Kinki region Japan Earthquake) Inland Earthquake Concern about critical national operations Tokyyqo Inland Earthquake Rate of earthquake production over 30 years: approx 70% (Magnitude 7 in southern Kanto area) Oceanic earthquake Inland earthquake Rate of earthquake occurrence is by Ministry of Education, Culture, Sports, Science and Technology Planning and Review for Countermeasures Against Earthquakes (1) Estimate distribution of seismic intensity, tsunami height, etc. -

ISC-GEM Global Instrumental Earthquake Catalogue (1900-2009)
ISC-GEM Global Instrumental Earthquake Catalogue (1900-2009) GEM Technical Report 2012-01 V1.0.0 Storchak D.A., D. Di Giacomo, I. Bondár, J. Harris, E.R. Engdahl, W.H.K. Lee, A. Villaseñor, P. Bormann, and G. Ferrari Geological, earthquake and geophysical data GEM GLOBAL EARTHQUAKE MODEL ISC-GEM Global Instrumental Earthquake Catalogue (1900-2009) GEM Technical Report 2012-01 Version: 1.0.0 Date: July 2012 Authors*: Storchak D.A., D. Di Giacomo, I. Bondár, J. Harris, E.R. Engdahl, W.H.K. Lee, A. Villaseñor, P. Bormann, and G. Ferrari (*) Authors’ affiliations: Dmitry Storchak, International Seismological Centre (ISC), Thatcham, UK Domenico Di Giacomo, International Seismological Centre (ISC), Thatcham, UK István Bondár, International Seismological Centre (ISC), Thatcham, UK James Harris, International Seismological Centre (ISC), Thatcham, UK Bob Engdahl, University of Colorado Boulder, USA Willie Lee, U.S. Geological Survey (USGS), Menlo Park, USA Antonio Villaseñor, Institute of Earth Sciences (IES) Jaume Almera, Barcelona, Spain Peter Bormann, Helmholtz Centre Potsdam GFZ German Research Centre for Geosciences, Germany Graziano Ferrari, Istituto Nazionale di Geofisica e Vulcanologia (INGV), Bologna, Italy Rights and permissions Copyright © 2012 GEM Foundation, International Seismological Centre, Storchak D.A., D. Di Giacomo, I. Bondár, J. Harris, E.R. Engdahl, W.H.K. Lee, A. Villaseñor, P. Bormann, and G. Ferrari Except where otherwise noted, this work is licensed under a Creative Commons Attribution 3.0 Unported License. The views and interpretations in this document are those of the individual author(s) and should not be attributed to the GEM Foundation. With them also lies the responsibility for the scientific and technical data presented. -

The Great East Japan Earthquake 2011
Tohoku University International Recovery Platform Kobe University Cabinet office of Japan Asian Disaster Reduction Center United Nations Office for Disaster Risk Reduction © IRP 2013 This report was jointly developed by Tohoku University, Kobe University, and individual experts with the support and supervision of the International Recovery Platform (IRP) and Prof. Yasuo Tanaka of University Tunku Abdul Rahman/Kobe University. International Recovery Platform Yasuo Kawawaki, Senior Recovery Expert Yoshiyuki Akamatsu, Senior Researcher Sanjaya Bhatia, Knowledge Management Officer Gerald Potutan, Recovery Expert The findings, interpretations, and conclusions expressed in this report do not necessarily reflect the views of IRP partners and governments. The information contained in this publication is provided as general guidance only. Every effort has been made to ensure the accuracy of the information. This report maybe freely quoted but acknowledgment of source is requested. INTERNATIONAL RECOVERY PLATFORM RECOVERY STATUS REPORT March 2013 The Great East Japan Earthquake 2011 TABLE OF CONTENTS TABLE OF CONTENTS ............................................................................................................... I FOREWORD ........................................................................................................................ 1 OVERVIEW OF THE GREAT EAST JAPAN EARTHQUAKE ............................................................ 3 TWO YEARS AFTER THE GREAT EAST JAPAN EARTHQUAKE: CURRENT STATUS AND THE CHALLENGES -

Japan Is One of the Most Earthquake-Prone Countries
Research on Urban Earthquake Engineering at Tokyo Tech. - Earthquake Disaster Mitigation - The 2011 Tohoku Earthquake (M9) Anticipated Tokyo Earthquake Technologies for Earthquake Disaster Mitigation Hiroaki Yamanaka, Center for Urban Earthquake Engineering Tokyo Institute of Technology 1 Japan is one of the most earthquake-prone countries. Epicenters of Large Earthquakes 2 Damage Earthquakes with more than 1,000 Fatalities in Japan since Meiji era 1894 Nobi Earthquake M8.0 7,300 1896 Sanriku Tsunami M8.3 22,000 1923 Kanto Earthquake M7.9 105,000 1927 Kita-Tango Earthquake M7.3 2,900 1933 Sanriku Tsunami M8.1 3,100 1943 Tottori Earthquake M7.2 1,100 1944 Tonankai Earthquake M7.9 1,000 1945 Mikawa Earthquake M6.8 2,000 1946 Nankai Earthquake M8.0 1,400 1948 Fukui Earthquake M7.1 3,800 1995 Kobe Earthquake M7.3 6,300 2011 Tohoku Earthquake M9.0 19,000 3 Strong Shaking during the 1995 Kobe Earthquake 4 Damage of the 1995 Kobe (Inland) Earthquake The 2011 off the Pacific coast of Tohoku Earthquake Origin Time: 14:46, March/11/2011 Magnitude: Mw9.0 Number of dead and missing: 19,000 Number of displaced people: 300,000 Number of damaged houses: 1,000,000 Direct monetary loss: 200 billion US$ 6 Tectonic Plates in the Japanese archipelago and surrounding areas Fault Plane of the Tohoku Earthquake 500km Length Pacific plate subducts Japan Islands, and Japan Islands spring up after HERP generating tsunami and shaking. 7 Video of Tsunami in Sendai From You Tube8 Onagawa 9 Seismic Intensity Map MM Intensity Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ XI JMA Intensity 4 5L 5U 6L 6U 7 after JMA The area of intensity 5 upper (MMI 8) or greater is approx. -

Contents 5 - 8 September, 2018 Lima Convention Center, Lima, Peru Disaster Risk Reduction for Natural Hazard MT5
12th International Symposium on Disaster Risk Management: Reconstruction Toward Resilient Cities (ISDRM 2018) Contents 5 - 8 September, 2018 Lima Convention Center, Lima, Peru Disaster risk reduction for natural hazard MT5. Capacity building for resilience in Reconstruction Earthquake history of Japan and lessons learned Reconstruction Towards Resilient Society: Research programs for earthquake risk reduction in Japan Japanese Experiences Peru-Japan SATREPS project Capacity building towards Build Back Better September 6, 2018 Fumio YAMAZAKI Professor, Ph.D., Graduate School of Engineering, Chiba University, Japan. Doctor Honoris Causa, National University of Engineering, Peru. 1 2 Estimated economic loss due to disasters in the world in 1975-2014. Mechanism behind the emergence of natural disasters (The values were converted to those in 2014.) Hazard Exposure Earthquakes, People, Property Floods, storms 2011 Thailand Disaster 2005 Hurricane Flood 1995 Kobe EQ Katrina Risk 2011 Tohoku EQ Vulnerability Susceptibility to natural hazards Disaster Risk Estimated Damage (US$ billion) Damage Estimated = Function (Hazard, Exposure, Vulnerability) Year 2008Wenchuan 3 Hand Book of Total Disaster Risk Management-Good Practices, ADRC, Japan, 2005 4 http://www.emdat.be/disaster_trends/index.html EQ Mechanism toward natural disaster reduction Disaster Cycle and Disaster Management Early Warning Basically unchanged Hazard Exposure but “climate change” Relocation of people & property Preparedness Response Disaster makes hazard bigger. from hazards -

International Aspects of the History of Earthquake Engineering
International Aspects Of the History of Earthquake Engineering Part I February 12, 2008 Draft Robert Reitherman Executive Director Consortium of Universities for Research in Earthquake Engineering This draft contains Part I: Acknowledgements Chapter 1: Introduction Chapter 2: Japan The planned contents of Part II are chapters 3 through 6 on China, India, Italy, and Turkey. Oakland, California 1 Table of Contents Acknowledgments .......................................................................................................................i Chapter 1 Introduction ................................................................................................................1 “Earthquake Engineering”.......................................................................................................1 “International” ........................................................................................................................3 Why Study the History of Earthquake Engineering?................................................................4 Earthquake Engineering History is Fascinating .......................................................................5 A Reminder of the Value of Thinking .....................................................................................6 Engineering Can Be Narrow, History is Broad ........................................................................6 Respect: Giving Credit Where Credit Is Due ..........................................................................7 The Importance -

Ings Damaged During the Recent Large Earthquakes in Japan
16th World Conference on Earthquake Engineering, 16WCEE 2017 Santiago Chile, January 9th to 13th 2017 Paper N° 4747 (Abstract ID) Registration Code: S-L1472725668 STUDY ON DAMAGE AND SEISMIC PERFORMANCE OF TIMBER BUILD- INGS DAMAGED DURING THE RECENT LARGE EARTHQUAKES IN JAPAN T. Tsuchimoto(1), N. Kawai(2), T. Nakagawa(3) (1) Chief Research Engineer, Building Research Institute, [email protected] (2) Professor, Kogakuin University, [email protected] (3) Senior Research Officer, National Institute for Land and Infrastructure Management, MLIT, [email protected] Abstract It is said that Japan has come to the term of seismic activity. Once, the damage of 1948 Fukui Earthquake triggered the establishment of Building Standard Law of Japan including the seismic regulation. The regulation for timber building adopted the way to set up enough shear wall by using the brace. After that, the regulations were reformed and revised several times at every damage due to earthquake. The required shear wall length increased at every revision of regulation. Timber buildings in Japan were damaged due to large earthquake since 2000, for example, 2000 West of Tottori Pref., 2004 Chuetsu, 2005 Fukuoka west off the coast, 2007 Noto Peninsula, 2007 offshore of Chuetsu, 2011 off the Pacific coast of Tohoku earthquake and 2014 Nagano Kamishiro Fault. The damage to timber buildings due to every earthquake was surveyed on site. Several wood houses were picked up and investigated in detail, for example, floor plans, shear wall length, damage states and structural specification. The reason and the characteristic of damage were discussed. The results of these surveys and studies were summarized as follows; - The 14 major earthquake suffering heavy damage to wood houses has occurred after the year of 2000. -

Title Recurrence of the Large Earthquakes Associated with The
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Kyoto University Research Information Repository Recurrence of the Large Earthquakes associated with the Fukui Title Earthquake Fault, as Derived from Subsurface Structure, Topography and the Present Day Seismic Activity Author(s) TAKEUCHI, Fumiaki Bulletin of the Disaster Prevention Research Institute (1989), Citation 39(4): 91-127 Issue Date 1989-12 URL http://hdl.handle.net/2433/124963 Right Type Departmental Bulletin Paper Textversion publisher Kyoto University Bull. Disas. Prey. Res. Inst., Kyoto Univ., Vol. 39, Part 4, No. 343, December, 1989 91 Recurrence of the Large Earthquakes associated with the Fukui Earthquake Fault, as Derived from Subsurface Structure, Topography and the Present Day Seismic Activity By Fumiaki TAKEUCHI (Manuscript received September 4th, 1989) Abstract Very little has been known about the Fukui earthquake fault, in spite of the fact that it generated one of the largest inland earthquakes in Japan, the 1948 Fukui earthquake (M=7.1). Thus its recur- rence characteristics have also been unknown. One main reason for this lack of knowledge of the fault is that its epicentral area is covered by thick deposits. We carried out a number of geophysical explorations, such as gravity, geomagnetic total force and microtremor measurements, to estimate the location and the vertical offset of the Fukui earthquake fault. The fault is located with a vertical offset of about 200 m, beneath the fissure zone that were caused by the 1948 earthquake. Because the vertical displacement associated with the 1948 event was roughly 1 m, we concluded that earthquakes of a similar size to the 1948 event have recurred 200 times on the same fault. -

EARTHQUAKE INSURANCE in JAPAN July 2014
EARTHQUAKE INSURANCE IN JAPAN July 2014 General Insurance Rating Organization of Japan (GIROJ) Preface Japan is a country that has large numbers of natural disasters due to such things as typhoons, earthquakes and volcanic eruptions, and, in particular, as it is the world’s most earthquake-afflicted country, massive earthquake disasters have occurred frequently. The general insurance (Non- life) system in Japan commenced in the latter half of the 19th century, when Japan was reincarnated into a modern state. However, though the necessity for earthquake insurance was proclaimed and considered every time an earthquake disaster occurred, there was great difficulty in establishing such insurance, since there was a possibility of causing huge amounts of loss once a large-scale earthquake occurred. As a result of considerations by the general insurance companies and the government, with the Niigata Earthquake in 1964 as the turning point, by limiting the coverage and amount insured and other means, and through acceptance of reinsurance by the government, earthquake insurance systems for residences and household goods were finally established in 1966. Afterwards, in response to the various needs of the insurance users whenever earthquake disaster occurred, the earthquake insurance systems have been revised many times and the coverage and amount insured, etc., have been broadly improved. In addition, in order to maintain more reasonable rate, reconsideration has been given in rating for earthquake insurance, in reflection of the results, etc., of Japan’s world class, leading edge earthquake research. This book explains about “earthquake insurance in Japan,” which is characterized in these various ways, and we hope it will assist you in understanding the subject more deeply.