Rate/State Coulomb Stress Transfer Model for the CSEP Japan Seismicity Forecast
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Coulomb Stresses Imparted by the 25 March
LETTER Earth Planets Space, 60, 1041–1046, 2008 Coulomb stresses imparted by the 25 March 2007 Mw=6.6 Noto-Hanto, Japan, earthquake explain its ‘butterfly’ distribution of aftershocks and suggest a heightened seismic hazard Shinji Toda Active Fault Research Center, Geological Survey of Japan, National Institute of Advanced Industrial Science and Technology (AIST), site 7, 1-1-1 Higashi Tsukuba, Ibaraki 305-8567, Japan (Received June 26, 2007; Revised November 17, 2007; Accepted November 22, 2007; Online published November 7, 2008) The well-recorded aftershocks and well-determined source model of the Noto Hanto earthquake provide an excellent opportunity to examine earthquake triggering associated with a blind thrust event. The aftershock zone rapidly expanded into a ‘butterfly pattern’ predicted by static Coulomb stress transfer associated with thrust faulting. We found that abundant aftershocks occurred where the static Coulomb stress increased by more than 0.5 bars, while few shocks occurred in the stress shadow calculated to extend northwest and southeast of the Noto Hanto rupture. To explore the three-dimensional distribution of the observed aftershocks and the calculated stress imparted by the mainshock, we further resolved Coulomb stress changes on the nodal planes of all aftershocks for which focal mechanisms are available. About 75% of the possible faults associated with the moderate-sized aftershocks were calculated to have been brought closer to failure by the mainshock, with the correlation best for low apparent fault friction. Our interpretation is that most of the aftershocks struck on the steeply dipping source fault and on a conjugate northwest-dipping reverse fault contiguous with the source fault. -

Improved Detection and Coulomb Stress Computations for Gas-Related, Shallow Seismicity, in the Western Sea of Marmara
1 Earth and Planetary Science Letters Archimer May 2019, Volume 513 Pages 113-123 https://doi.org/10.1016/j.epsl.2019.02.021 https://archimer.ifremer.fr https://archimer.ifremer.fr/doc/00484/59522/ Improved detection and Coulomb stress computations for gas-related, shallow seismicity, in the Western Sea of Marmara Tary Jean-Baptiste 1, * , Géli Louis 2, Lomax Anthony 3, Batsi Evangelia 2, Riboulot Vincent 2, Henry Pierre 4 1 Departamento de Geociencias, Universidad de los Andes, Bogotá, Colombia 2 Institut Français de Recherche pour l'Exploitation de la Mer (IFREMER), Marine Geosciences Research Unit, BP 70, 29280 Plouzané, France 3 ALomax Scientific, 320 Chemin des Indes, 06370, Mouans Sartoux, France 4 Aix Marseille University, CNRS, IRD, INRA, Collège de France, CEREGE, Aix-en-Provence, France * Corresponding author : Jean-Baptiste Tary, email address : [email protected] Abstract : The Sea of Marmara (SoM) is a marine portion of the North Anatolian Fault (NAF) and a portion of this fault that did not break during its 20th century earthquake sequence. The NAF in the SoM is characterized by both significant seismic activity and widespread fluid manifestations. These fluids have both shallow and deep origins in different parts of the SoM and are often associated with the trace of the NAF which seems to act as a conduit. On July 25th, 2011, a 5 strike-slip earthquake occurred at a depth of about 11.5 km, triggering clusters of seismicity mostly located at depths shallower than 5 km, from less than a few minutes up to more than 6 days after the mainshock. -

The Kobe (Hyogo-Ken Nanbu), Japan, Earthquake of January 16, 1995
The Kobe (Hyogo-ken Nanbu), Japan, Earthquake of January 16, 1995 A report of preliminary observations prepared by Hiroo Kanamori California Institute of Technology he Kobe earthquake of January 16, 1995, is one of the Daishinsai (A major earthquake disaster in the Osaka-Kobe most damaging earthquakes in the recent history of area)." As ofJanuary 29, 1995, the casualty toll reached 5,094 T Japan. This earthquake is also called "The Hyogo-ken dead, 13 missing and 26,798 injured. Nanbu (Southern part of Hyogo prefecture) earthquake," This article presents some background on the earth- and the disaster caused by it is referred to as "Hanshin quake and its setting and a summary of some preliminary seismological results obtained by various investigators. The Japan Meteorological Agency ,/" e</-..... 0MA) located this earthquake at 34.60~ 135.00~ depth=22 km, origin time= 1943Tottori 1927Tango 1948 Fukui // '/~;/",~ 7 05:46:53.9, 1/17/1995JST, (20:46:53.9, 1/16/ (M=7.2) (M=7.a) (M=7.~) / ,.~o~.>:'/ k i 1995 GMT) with a JMA magnitude Mj=7.2 rS.. 7a (Figure 1). The epicenter is close to the city of Kobe (population, about 1.4 million), ap- proximately 200 km away from the Nankai trough (the major plate boundary between ,0., ~" "v"~.M "-'-" ~ the Philippine Sea and the Eurasia plates), and about 40 km from the Median Tectonic Line. In this sense this earthquake can be called an intraplate earthquake. In central- ,,o, oi ~J/ ,~ western Japan four major intraplate earth- .... "...C%<,,. ",z,.-.. :~/.S,,.-/" I \,q' _.. s , quakes have occurred since 1890 (Figure 1): . -

Great East Japan Earthquake, Jr East Mitigation Successes, and Lessons for California High-Speed Rail
MTI Funded by U.S. Department of Services Transit Census California of Water 2012 Transportation and California Great East Japan Earthquake, Department of Transportation JR East Mitigation Successes, and Lessons for California High-Speed Rail MTI ReportMTI 12-02 MTI Report 12-37 December 2012 MINETA TRANSPORTATION INSTITUTE MTI FOUNDER Hon. Norman Y. Mineta The Mineta Transportation Institute (MTI) was established by Congress in 1991 as part of the Intermodal Surface Transportation Equity Act (ISTEA) and was reauthorized under the Transportation Equity Act for the 21st century (TEA-21). MTI then successfully MTI BOARD OF TRUSTEES competed to be named a Tier 1 Center in 2002 and 2006 in the Safe, Accountable, Flexible, Efficient Transportation Equity Act: A Legacy for Users (SAFETEA-LU). Most recently, MTI successfully competed in the Surface Transportation Extension Act of 2011 to Founder, Honorable Norman Thomas Barron (TE 2015) Ed Hamberger (Ex-Officio) Michael Townes* (TE 2014) be named a Tier 1 Transit-Focused University Transportation Center. The Institute is funded by Congress through the United States Mineta (Ex-Officio) Executive Vice President President/CEO Senior Vice President Department of Transportation’s Office of the Assistant Secretary for Research and Technology (OST-R), University Transportation Secretary (ret.), US Department of Strategic Initiatives Association of American Railroads Transit Sector Transportation Parsons Group HNTB Centers Program, the California Department of Transportation (Caltrans), and by private grants and donations. Vice Chair Steve Heminger (TE 2015) Hill & Knowlton, Inc. Joseph Boardman (Ex-Officio) Executive Director Bud Wright (Ex-Officio) Chief Executive Officer Metropolitan Transportation Executive Director The Institute receives oversight from an internationally respected Board of Trustees whose members represent all major surface Honorary Chair, Honorable Bill Amtrak Commission American Association of State transportation modes. -

Rupture Process of the 2019 Ridgecrest, California Mw 6.4 Foreshock and Mw 7.1 Earthquake Constrained by Seismic and Geodetic Data, Bull
Rupture process of the 2019 Ridgecrest, M M California w 6.4 Foreshock and w 7.1 Earthquake Constrained by Seismic and Geodetic Data Kang Wang*1,2, Douglas S. Dreger1,2, Elisa Tinti3,4, Roland Bürgmann1,2, and Taka’aki Taira2 ABSTRACT The 2019 Ridgecrest earthquake sequence culminated in the largest seismic event in California M since the 1999 w 7.1 Hector Mine earthquake. Here, we combine geodetic and seismic data M M to study the rupture process of both the 4 July w 6.4 foreshock and the 6 July w 7.1 main- M shock. The results show that the w 6.4 foreshock rupture started on a northwest-striking right-lateral fault, and then continued on a southwest-striking fault with mainly left-lateral M slip. Although most moment release during the w 6.4 foreshock was along the southwest- striking fault, slip on the northwest-striking fault seems to have played a more important role M ∼ M in triggering the w 7.1 mainshock that happened 34 hr later. Rupture of the w 7.1 main- shock was characterized by dominantly right-lateral slip on a series of overall northwest- striking fault strands, including the one that had already been activated during the nucleation M ∼ of the w 6.4 foreshock. The maximum slip of the 2019 Ridgecrest earthquake was 5m, – M located at a depth range of 3 8kmnearthe w 7.1 epicenter, corresponding to a shallow slip deficit of ∼ 20%–30%. Both the foreshock and mainshock had a relatively low-rupture veloc- ity of ∼ 2km= s, which is possibly related to the geometric complexity and immaturity of the eastern California shear zone faults. -

Triggered Earthquakes Suppressed by an Evolving Stress Shadow from a Propagating Dyke
Triggered earthquakes suppressed by an evolving stress shadow from a propagating dyke Robert G. Green1 Tim Greenfield1 Robert S. White1 *Corresponding Author: Green, Robert G. [email protected] CONTACT AUTHOR TO REQUEST AN ARTICLE PDF 1Bullard Laboratories, Department of Earth Sciences, University of Cambridge, Madingley Road, Cambridge, UK, CB3 0EZ. Small static stress increases resulting from large radiation patterns have also been invoked to explain earthquakes may trigger aftershock earthquake aftershock clustering3, but dynamic triggering cannot swarms, while stress reductions may reduce impart a stress shadow that would reduce seismicity earthquake failure rates1,2 (stress shadowing). in response to stress decrease at a given location6. However, seismic waves from large earthquakes also Many studies have suggested that in regions where cause transient dynamic stresses which may trigger the static stress is decreased, aftershocks are rare or seismicity3,4. This makes it difficult to separate the seismicity rates are reduced as a consequence of the relative influence of static and dynamic stress negative stress shadow caused by the fault changes on aftershocks. Here we present an rupture1,6,7,8,9. However, convincing observations of excellent demonstration of static stress triggering the stress shadowing effect have been notoriously and shadowing during the intrusion of a 46 km long, hard to demonstrate, and some have argued that 5 m wide igneous dyke in central Iceland. During the there is a lack of evidence that they exist at all3,10,11. emplacement, bursts of seismicity 5‒15 km away The challenge has been to demonstrate convincing from the dyke are first triggered and then abruptly and significant earthquake rate drops that correlate switched off as the dyke tip propagated away from unambiguously with a stress decrease, because a high Bárðarbunga volcano and along the neovolcanic rift preceding seismicity rate is required. -

3-D Numerical Modeling of Coupled Crustal Deformation and Fluid
3-D Numerical Modeling of Coupled Crustal Deformation and Fluid Pressure Interactions Final Technical Report U. S. Geological Survey Award No. 08HQGR0031 Lorraine W. Wolf Ming-Kuo Lee Auburn University Department of Geology and Geography 210 Petrie Hall Auburn, Alabama 36849 Ph: 334-844-4282 Fax: 334-844-4486 [email protected]; [email protected] 1/10/08-12/31/09 Program Element II ABSTRACT This report summarizes the results from a project aimed at investigating the interrelationships of crustal deformation and pore fluid pressures. The project had three main goals: (1) to develop an algorithm for simulating crustal deformation and fluid flow processes, (2) to implement and validate numerical models based on selected benchmark hydrogeophysical problems related to specified boundary conditions, and (3) to use the numerical simulations to explore poroelastic processes in realistic geologic domains. The results of the project should be useful for reducing seismic hazard by increasing our understanding of fluid pressures in postseismic deformation and by providing a coupled crustal deformation and pore pressure propagation modeling tool available to others for use in exploring the poroelastic response of brittle crustal rocks and sedimentary basins to strong earthquakes. The codes developed as part of this grant, referred to herein as PFLOW, are described in this report. PFLOW is a 3-D time- dependent pore-pressure diffusion model developed to investigate the response of pore fluids to the crustal deformation generated by strong earthquakes in heterogeneous geologic media. Given crustal strain generated by changes in Coulomb stress, this MATLAB-based code uses Skempton's coefficient to calculate resulting initial change in fluid pressure (initial condition). -

A Discussion on the Relations of Site Effect and Damage of Wooden Houses Using with Microtremors in Fukui Plain Affected by the 1948 Fukui Earthquake
13th World Conference on Earthquake Engineering Vancouver, B.C., Canada August 1-6, 2004 Paper No. 722 A DISCUSSION ON THE RELATIONS OF SITE EFFECT AND DAMAGE OF WOODEN HOUSES USING WITH MICROTREMORS IN FUKUI PLAIN AFFECTED BY THE 1948 FUKUI EARTHQUAKE. Norio ABEKI*1 and Toshiyuki MAEDA*2 SUMMARY Authors observed microtremors in Fukui Plain to discuss on the relationships between dynamic characteristics of surface geology and the damages of wooden houses caused by the 1948 Fukui Earthquake. By the distribution maps of predominant periods using H/V spectral ratio and damaged ratios of wooden houses, the distribution of the short periods corresponded to the low damaged ratios. And the areas of predominant long periods distributed on alluvial deposit in the western part from the earthquake fault. The high damage ratios at the sites of alluvial deposit are located within 8km from the earthquake fault, but the ratios decreased and varied widely in the areas farther than 8km. The predominant periods are related with the thickness of alluvial deposit. We can conclude that the earthquake damages were related with the dynamic characteristics of surface geology in this area. INTRODUCTION The 1948 Fukui Earthquake occurred at July 28, 1948 and it affected the buildings, railway, road, bridges and another social facilities. 3,763 persons had been killed, 36,134 houses completely and 11,816 houses partially destroyed, and 3,851 houses burned down by The Earthquake.1) The epicenter located at Maruoka town where is in the Fukui Plain, and the seismic fault went through from south to north in the plain. -
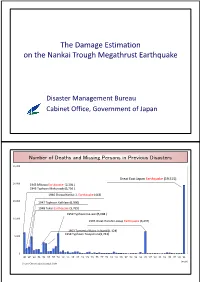
The Damage Estimation on the Nankai Trough Megathrust
The Damage Estimation onthen the Nankai Trough Megathrust Earthquake Disaster Management Bureau Cabinet Office, Government of Japan Number of Deaths and Missing Persons in Previous Disasters 25, 000 Great East Japan Earthquake (19,515) 20,000 1945 Mikawa Earthquake (2,306 ) 1945 Typhoon Makurazaki(3,756 ) 1946 Showa Nankai 1, Earthquake (443) 15,000 1947 Typhoon Kathleen(1,930) 1948 Fukui Earthquake (3,769) 1959 Typhoon Ise-wan(5,098 ) 10,000 1995 Great Hanshin-Awaji Earthquake (6,437) 1953 Torrential Rains in Nanki(1,124) 1954 Typhoon Touyamaru(1,761) 5,000 0 '45 '47 '49 '51 '53 '55 '57 '59 '61 '63 '65 '67 '69 '71 '73 '75 '77 '79 '81 '83 '85 '87 '89 '91 '93 '95 '97 '99 '01 '03 '05 '07 '09 '11 (year) Source: Chronological Scientific Table Large Earthquakes Reviewed by the Central Disaster Management Council Super wide-area earthquake extending to western Japan Tokikai Eart hqua ke Huge tsunami over 20 meters Tonankai, Nankai Earthquake Rate of earthquake production over 30 years: Oceanic-type earthquakes 60 ~ 70% in the vicinity of the Japan and Chishima Trenches Concerns about neglected timber buildings and Unknown ( Miyagi offshore cultural assets earthquake production rate over 30 years: 99% prior to the Great East Cyubu region, Kinki region Japan Earthquake) Inland Earthquake Concern about critical national operations Tokyyqo Inland Earthquake Rate of earthquake production over 30 years: approx 70% (Magnitude 7 in southern Kanto area) Oceanic earthquake Inland earthquake Rate of earthquake occurrence is by Ministry of Education, Culture, Sports, Science and Technology Planning and Review for Countermeasures Against Earthquakes (1) Estimate distribution of seismic intensity, tsunami height, etc. -

What Is Better Than Coulomb Failure Stress?
PUBLICATIONS Geophysical Research Letters RESEARCH LETTER What Is Better Than Coulomb Failure Stress? A Ranking 10.1002/2017GL075875 of Scalar Static Stress Triggering Mechanisms Key Points: from 105 Mainshock-Aftershock Pairs • What are good stress based predictors of aftershock locations? Brendan J. Meade1,2 , Phoebe M. R. DeVries1, Jeremy Faller2, Fernanda Viegas2, • Coulomb failure stress is a poor 2 predictor, but the third invariant of the and Martin Wattenberg stress tensor is quite good 1 2 • Large-scale analysis of mainshocks Department of Earth and Planetary Sciences, Harvard University, Cambridge, MA, USA, Google, Inc., Cambridge, MA, USA and aftershocks suggests very different patterns than commonly assumed Abstract Aftershocks may be triggered by the stresses generated by preceding mainshocks. The temporal frequency and maximum size of aftershocks are well described by the empirical Omori and Bath laws, but Supporting Information: spatial patterns are more difficult to forecast. Coulomb failure stress is perhaps the most common criterion • Supporting Information S1 invoked to explain spatial distributions of aftershocks. Here we consider the spatial relationship between patterns of aftershocks and a comprehensive list of 38 static elastic scalar metrics of stress (including stress Correspondence to: tensor invariants, maximum shear stress, and Coulomb failure stress) from 213 coseismic slip distributions B. J. Meade, [email protected] worldwide. The rates of true-positive and false-positive classification of regions with and without aftershocks are assessed with receiver operating characteristic analysis. We infer that the stress metrics that are most consistent with observed aftershock locations are maximum shear stress and the magnitude of the second Citation: Meade, B. -

ISC-GEM Global Instrumental Earthquake Catalogue (1900-2009)
ISC-GEM Global Instrumental Earthquake Catalogue (1900-2009) GEM Technical Report 2012-01 V1.0.0 Storchak D.A., D. Di Giacomo, I. Bondár, J. Harris, E.R. Engdahl, W.H.K. Lee, A. Villaseñor, P. Bormann, and G. Ferrari Geological, earthquake and geophysical data GEM GLOBAL EARTHQUAKE MODEL ISC-GEM Global Instrumental Earthquake Catalogue (1900-2009) GEM Technical Report 2012-01 Version: 1.0.0 Date: July 2012 Authors*: Storchak D.A., D. Di Giacomo, I. Bondár, J. Harris, E.R. Engdahl, W.H.K. Lee, A. Villaseñor, P. Bormann, and G. Ferrari (*) Authors’ affiliations: Dmitry Storchak, International Seismological Centre (ISC), Thatcham, UK Domenico Di Giacomo, International Seismological Centre (ISC), Thatcham, UK István Bondár, International Seismological Centre (ISC), Thatcham, UK James Harris, International Seismological Centre (ISC), Thatcham, UK Bob Engdahl, University of Colorado Boulder, USA Willie Lee, U.S. Geological Survey (USGS), Menlo Park, USA Antonio Villaseñor, Institute of Earth Sciences (IES) Jaume Almera, Barcelona, Spain Peter Bormann, Helmholtz Centre Potsdam GFZ German Research Centre for Geosciences, Germany Graziano Ferrari, Istituto Nazionale di Geofisica e Vulcanologia (INGV), Bologna, Italy Rights and permissions Copyright © 2012 GEM Foundation, International Seismological Centre, Storchak D.A., D. Di Giacomo, I. Bondár, J. Harris, E.R. Engdahl, W.H.K. Lee, A. Villaseñor, P. Bormann, and G. Ferrari Except where otherwise noted, this work is licensed under a Creative Commons Attribution 3.0 Unported License. The views and interpretations in this document are those of the individual author(s) and should not be attributed to the GEM Foundation. With them also lies the responsibility for the scientific and technical data presented. -
![Long-Term Monitoring Experiment in Geologically Active Regions of Europe Prone to Natural Hazards: the Supersite Concept]](https://docslib.b-cdn.net/cover/3094/long-term-monitoring-experiment-in-geologically-active-regions-of-europe-prone-to-natural-hazards-the-supersite-concept-2233094.webp)
Long-Term Monitoring Experiment in Geologically Active Regions of Europe Prone to Natural Hazards: the Supersite Concept]
THEME [ENV.2012.6.4-2] [Long-term monitoring experiment in geologically active regions of Europe prone to natural hazards: the Supersite concept] * Annex I - "Description of Work" !" # $%& ' '( &) ' * ' # +,-./0 1 & 2,/2/,,- Table of Contents Part A A.1 Project summary ......................................................................................................................................4 A.2 List of beneficiaries ..................................................................................................................................5 A.3 Overall budget breakdown for the project ............................................................................................... 7 Workplan Tables WT1 List of work packages ............................................................................................................................1 WT2 List of deliverables .................................................................................................................................2 WT3 Work package descriptions ................................................................................................................... 9 Work package 1......................................................................................................................................9 Work package 2....................................................................................................................................12 Work package 3....................................................................................................................................16