DOCSLIB.ORG

Assessing Model Sensitivity in Ancestral Area Reconstruction Using

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Assessing Model Sensitivity in Ancestral Area Reconstruction Using Journal of Biogeography (J. Biogeogr.) (2014) 41, 1414–1427 ORIGINAL Assessing model sensitivity in ancestral ARTICLE area reconstruction using LAGRANGE:a case study using the Colchicaceae family Juliana Chacon* and Susanne S. Renner Department of Biology, University of Munich, ABSTRACT 80638 Munich, Germany Aim Likelihood analyses of ancestral ranges require a parameterized model that consists of a time-calibrated phylogeny, an ‘adjacency matrix’ of allowed or forbidden area connections, and an ‘area–dispersal’ matrix with probabilities for discrete periods of time. The approach is implemented in the software Lag- range. Because it can incorporate information about past continental posi- tions, the approach has been used in historical biogeographical studies of relatively old clades. Surprisingly, no study has evaluated the interactions among these input matrices. Here we use the lily family Colchicaceae and arti- ficial data to study the relative effect of the input matrices on final estimates. Location Africa, Australia, Eurasia, North America and South America. Methods Using eight plastid, mitochondrial and nuclear DNA regions from 85 of the c. 280 species of Colchicaceae (representing all genera and the entire geographical range) and relevant outgroups, we obtained a well-resolved phy- logeny dated with a molecular clock. We then assigned species to six geograph- ical distributions and carried out 22 Lagrange runs in which we modified the adjacency and dispersal matrices, the latter with zero, two or four time periods and one, three or five dispersal probabilities. For a second data set, the areas at deep nodes in the empirical tree were modified by shuffling species distribu- tions. Models were compared based on global log-likelihoods. Results The adjacency matrix strongly determined the outcome, while time slices and dispersal probability categories had minor effects. Ancestral areas reconstructed at most nodes were unaffected by the different input matrices. Colchicaceae are likely to have originated in Cretaceous East Gondwana, ini- tially diversified in Australia (c. 67 Ma), reached southern Africa during the Palaeocene–Eocene, and from there extended their range to Southeast Asia (probably through Arabia) and then North America (through Beringia). Main conclusions At least in small data sets, Lagrange models should be tested with sensitivity analyses as carried out here, concentrating on con- strained versus unconstrained adjacency matrices, and it should be good prac- tice to report the set-up of both input matrices, not just the dispersal matrix, which is the less decisive of the two. Keywords *Correspondence: Juliana Chacon, Systematic Adjacency matrix, ancestral area reconstruction, area–dispersal matrix, chron- Botany and Mycology, University of Munich, Menzinger Str. 67, 80638 Munich, Germany. ogram, Colchicaceae, geographical range evolution, Gondwana, historical bio- E-mail: [email protected] geographical methods, likelihood models, palaeogeography. 1414 http://wileyonlinelibrary.com/journal/jbi ª 2014 John Wiley & Sons Ltd doi:10.1111/jbi.12301 When to keep ancestral area reconstruction models simple will only be preferred over a dispersal scenario if it is congru- INTRODUCTION ent with the a priori accepted geological context (Ree et al., The rise of molecular clock dating as a tool in historical bio- 2005). An absence of expansion into another area could be geographical analysis has been accompanied by the develop- just that or could be a result of extinction in that area; both ment of new methods of ancestral area reconstruction (AAR). are captured by extremely low dispersal probability values. A The most sophisticated of these methods, Likelihood Analysis user can build as many dispersal matrices for different of Geographic Range Evolution or Lagrange (Ree et al., periods of time (‘time slices’) as deemed appropriate. 2005; Ree & Smith, 2008), is model-based and has been the The components described above imply that Lagrange method of choice for deep-time biogeographical studies requires more ad hoc parameter values than other biogeo- because it allows the incorporation of palaeogeographical graphical methods. Studies using the program have differed data. This is achieved through the dispersal–extinction–clado- considerably both in model details and in the reporting of genesis (DEC) model (Ree & Smith, 2008), which uses four model parameterization (Table 1 in Nauheimer et al., 2012, components: (1) a fully resolved chronogram; (2) a species provides an overview). For example, studies have left adja- distribution matrix denoting a species’ presence in a set of cency matrices unconstrained (Carlson et al., 2012) or con- geographical areas; (3) an adjacency matrix specifying allowed strained (Clayton et al., 2009), but without testing how this and forbidden ranges; and (4) an area–dispersal matrix speci- interacted with the other input matrices or how an alterna- fying dispersal probabilities between areas. The DEC model tive treatment would have impacted the global model likeli- assumes that two stochastic processes underlie the range evo- hood. Similarly, the probability of dispersal between lution of a species in the absence of lineage divergence: range Australia and South America during the Cretaceous (145– expansion through dispersal between areas and range contrac- 66 Ma) in different studies was assigned a probability of tion through extinction within an area. Therefore all models P = 1 (Buerki et al., 2011: time slices before 60 and before have two free parameters: a mean rate of dispersal between 80 Ma), P = 0.5 (Mao et al., 2012: time slice between 105 the areas i and j, Dij, and a mean rate of extinction in the and 70 Ma) or P = 0.01 (Nauheimer et al., 2012: time slices area i, Ei (Ree & Smith, 2008). The likelihood function then of 150–90 Ma and 90–30 Ma). The number of probability integrates over the conditional likelihoods of all ancestral categories also has differed from author to author, so far states at every internal node weighted by their prior probabil- ranging from five (Mao et al., 2012; P = 0.1, 0.25, 0.5, 0.75 ity (set by the user-defined input matrices), proceeding and 1) to three (Buerki et al., 2011; P = 0.01, 0.5 and 1). backwards from the tips of the tree to its root. We know of five studies that have attempted to use As regards component (1), the input chronogram provides model comparison to assess model fit. A problem here is the time-calibrated nodes and branches for which the proba- that there is no test statistic suitable for assessing the per- bility of ancestor–descendant area change is calculated. formance of DEC models because they have the same num- Component (2), the species distribution matrix, allows users ber of free parameters and are not hierarchically nested. to define areas appropriate for their clade and research ques- Therefore, likelihood ratio tests or the Akaike information tion, with the limitation that the number of biogeographical criterion (AIC) are not applicable (see Posada & Buckley, parameters to estimate from the data increases exponentially 2004). As a workaround, workers have used the global like- with the number of areas, decreasing the inferential power of lihood calculated by Lagrange to compare models and the the model (Ree & Sanmartın, 2009). Studies have used from rule that a two log-likelihood unit difference between mod- three to 15 geographical areas (see Table 1 in Nauheimer els indicates significance (Edwards, 1992). Using this et al., 2012), seeking a balance between the dispersion of tips approach, Couvreur et al. (2011) and Baker & Couvreur [species] across areas (hence the potential inferred ‘area (2013) found that their models with zero time slices were switches’ at nodes deep in the tree) and the risk of having significantly more likely than constrained models with five many singletons (areas occupied by a single tip taxon). Com- time slices. In a large data set of Cupressaceae, Mao et al. ponent (3), the adjacency matrix, is a presence–absence (2012) similarly compared the likelihoods of models with matrix in which a user defines composite ranges allowed or four, five, six, seven or eight time slices. The migration forbidden in the model (for example, the combined continent probabilities ranged from 0.1 for well-separated areas to 1.0 Laurasia but not a combined Asia and Australia). It is similar for contiguous landmasses. They found that the most com- to the cost matrix used in the program diva (Ronquist, plex (eight-time-slice) model had the best global likelihood. 1997), except that diva does not have a configuration option By contrast, in a large Araceae matrix, the likelihood of a for excluding discontinuous ranges. For component (4), the simpler (three-time-slice) model was higher than that of a area–dispersal matrix, the user specifies values (such as 1, 0.5, more complex (four-time-slice) model (Nauheimer et al., 0.01 or 0) for dispersal probabilities between areas based on 2012). The only studies to test the effects of constrained prior notions about range expansion. These values become and unconstrained adjacency matrices are an analysis of area-specific scaling factors for the program’s calculation of Psychotria in Hawaii (Ree & Smith, 2008) and one of the average rate of dispersal. Vicariance scenarios are not Cyrtandra in the Pacific Islands (Clark et al., 2008); both favoured a priori. If descendants are restricted to separate found that a constrained matrix fitted the data better than areas of the ancestral range, a vicariant speciation scenario an unconstrained one. Journal of Biogeography 41, 1414–1427 1415 ª 2014 John Wiley & Sons Ltd J. Chacon and S. S. Renner To advance the field of likelihood-based historical bioge- (Vinnersten & Reeves, 2003; Vinnersten & Manning, 2007; ography, we decided to investigate the interactions among del Hoyo & Pedrola-Monfort, 2008; Persson et al., 2011), the input matrices, number of time slices, dispersal probabil- while the best circumscription of Wurmbea is still unclear ity categories, and node/area/time slice ratio in an empirical (Thi et al., 2013).
Load more

Recommended publications
  • Plant List 2016
    Established 1990 PLANT LIST 2016 European mail order website www.crug-farm.co.uk CRÛG FARM PLANTS • 2016 Welcome to our 2016 list hope we can tempt you with plenty of our old favourites as well as some exciting new plants that we have searched out on our travels. There has been little chance of us standing still with what has been going on here in 2015. The year started well with the birth of our sixth grandchild. January into February had Sue and I in Colombia for our first winter/early spring expedition. It was exhilarating, we were able to travel much further afield than we had previously, as the mountainous areas become safer to travel. We are looking forward to working ever closer with the Colombian institutes, such as the Medellin Botanic Gardens whom we met up with. Consequently we were absent from the RHS February Show at Vincent Square. We are finding it increasingly expensive participating in the London shows, while re-branding the RHS February Show as a potato event hardly encourages our type of customer base to visit. A long standing speaking engagement and a last minute change of date, meant that we missed going to Fota near Cork last spring, no such problem this coming year. We were pleasantly surprised at the level of interest at the Trgrehan Garden Rare Plant Fair, in Cornwall. Hopefully this will become an annual event for us, as well as the Cornwall Garden Society show in April. Poor Sue went through the wars having to have a rush hysterectomy in June, after some timely results revealed future risks.
    [Show full text]
  • Guide to the Flora of the Carolinas, Virginia, and Georgia, Working Draft of 17 March 2004 -- LILIACEAE
    Guide to the Flora of the Carolinas, Virginia, and Georgia, Working Draft of 17 March 2004 -- LILIACEAE LILIACEAE de Jussieu 1789 (Lily Family) (also see AGAVACEAE, ALLIACEAE, ALSTROEMERIACEAE, AMARYLLIDACEAE, ASPARAGACEAE, COLCHICACEAE, HEMEROCALLIDACEAE, HOSTACEAE, HYACINTHACEAE, HYPOXIDACEAE, MELANTHIACEAE, NARTHECIACEAE, RUSCACEAE, SMILACACEAE, THEMIDACEAE, TOFIELDIACEAE) As here interpreted narrowly, the Liliaceae constitutes about 11 genera and 550 species, of the Northern Hemisphere. There has been much recent investigation and re-interpretation of evidence regarding the upper-level taxonomy of the Liliales, with strong suggestions that the broad Liliaceae recognized by Cronquist (1981) is artificial and polyphyletic. Cronquist (1993) himself concurs, at least to a degree: "we still await a comprehensive reorganization of the lilies into several families more comparable to other recognized families of angiosperms." Dahlgren & Clifford (1982) and Dahlgren, Clifford, & Yeo (1985) synthesized an early phase in the modern revolution of monocot taxonomy. Since then, additional research, especially molecular (Duvall et al. 1993, Chase et al. 1993, Bogler & Simpson 1995, and many others), has strongly validated the general lines (and many details) of Dahlgren's arrangement. The most recent synthesis (Kubitzki 1998a) is followed as the basis for familial and generic taxonomy of the lilies and their relatives (see summary below). References: Angiosperm Phylogeny Group (1998, 2003); Tamura in Kubitzki (1998a). Our “liliaceous” genera (members of orders placed in the Lilianae) are therefore divided as shown below, largely following Kubitzki (1998a) and some more recent molecular analyses. ALISMATALES TOFIELDIACEAE: Pleea, Tofieldia. LILIALES ALSTROEMERIACEAE: Alstroemeria COLCHICACEAE: Colchicum, Uvularia. LILIACEAE: Clintonia, Erythronium, Lilium, Medeola, Prosartes, Streptopus, Tricyrtis, Tulipa. MELANTHIACEAE: Amianthium, Anticlea, Chamaelirium, Helonias, Melanthium, Schoenocaulon, Stenanthium, Veratrum, Toxicoscordion, Trillium, Xerophyllum, Zigadenus.
    [Show full text]
  • Nuytsia the Journal of the Western Australian Herbarium 31: 197–202 Published Online 20 August 2020
    T.D. Macfarlane, A.P. Brown & C.J. French, Wurmbea flavanthera (Colchicaceae), a new species 197 Nuytsia The journal of the Western Australian Herbarium 31: 197–202 Published online 20 August 2020 Wurmbea flavanthera (Yellow-anthered Wurmbea, Colchicaceae), a new species from Western Australia’s Mid West region Terry D. Macfarlane1, Andrew P. Brown and Christopher J. French Western Australian Herbarium, Biodiversity and Conservation Science, Department of Biodiversity, Conservation and Attractions, Locked Bag 104, Bentley Delivery Centre, Western Australia 6983 1Corresponding author, email: [email protected] SHORT COMMUNICATION Wurmbea densiflora (Benth.) T.Macfarlane (Colchicaceae) is an attractive, small geophyte bearing several pink flowers, occurring in the northern Wheatbelt and adjacent rangelands of Western Australia. However, the species concept used in a revision of Wurmbea Thunb. in Australia (Macfarlane 1980, 1987) proves to be a mixture of two species, W. densiflora in the original sense of Bentham (1878) and a later-flowering, undescribed species. This second species was given the phrase nameW . sp. Paynes Find (C.J. French 1237), by which it has been known for some time (Western Australian Herbarium 1998–). The new species, having been well-researched in the field and Herbarium, is formally described below. The previous confusion between the two species was partly due to a lack of field knowledge and an inadequate appreciation of the relatively constrained flowering times ofWurmbea species. Wurmbea flavanthera T.Macfarlane, A.P.Br. & C.J.French, sp. nov. Type: 11.8 km north of Jose Street, Mullewa, on Carnarvon – Mullewa Road, west of road on a minor track, Western Australia, 17 August 2011, T.D.
    [Show full text]
  • Partial Flora Survey Rottnest Island Golf Course
    PARTIAL FLORA SURVEY ROTTNEST ISLAND GOLF COURSE Prepared by Marion Timms Commencing 1 st Fairway travelling to 2 nd – 11 th left hand side Family Botanical Name Common Name Mimosaceae Acacia rostellifera Summer scented wattle Dasypogonaceae Acanthocarpus preissii Prickle lily Apocynaceae Alyxia Buxifolia Dysentry bush Casuarinacea Casuarina obesa Swamp sheoak Cupressaceae Callitris preissii Rottnest Is. Pine Chenopodiaceae Halosarcia indica supsp. Bidens Chenopodiaceae Sarcocornia blackiana Samphire Chenopodiaceae Threlkeldia diffusa Coast bonefruit Chenopodiaceae Sarcocornia quinqueflora Beaded samphire Chenopodiaceae Suada australis Seablite Chenopodiaceae Atriplex isatidea Coast saltbush Poaceae Sporabolis virginicus Marine couch Myrtaceae Melaleuca lanceolata Rottnest Is. Teatree Pittosporaceae Pittosporum phylliraeoides Weeping pittosporum Poaceae Stipa flavescens Tussock grass 2nd – 11 th Fairway Family Botanical Name Common Name Chenopodiaceae Sarcocornia quinqueflora Beaded samphire Chenopodiaceae Atriplex isatidea Coast saltbush Cyperaceae Gahnia trifida Coast sword sedge Pittosporaceae Pittosporum phyliraeoides Weeping pittosporum Myrtaceae Melaleuca lanceolata Rottnest Is. Teatree Chenopodiaceae Sarcocornia blackiana Samphire Central drainage wetland commencing at Vietnam sign Family Botanical Name Common Name Chenopodiaceae Halosarcia halecnomoides Chenopodiaceae Sarcocornia quinqueflora Beaded samphire Chenopodiaceae Sarcocornia blackiana Samphire Poaceae Sporobolis virginicus Cyperaceae Gahnia Trifida Coast sword sedge
    [Show full text]
  • Alphabetical Lists of the Vascular Plant Families with Their Phylogenetic
    Colligo 2 (1) : 3-10 BOTANIQUE Alphabetical lists of the vascular plant families with their phylogenetic classification numbers Listes alphabétiques des familles de plantes vasculaires avec leurs numéros de classement phylogénétique FRÉDÉRIC DANET* *Mairie de Lyon, Espaces verts, Jardin botanique, Herbier, 69205 Lyon cedex 01, France - [email protected] Citation : Danet F., 2019. Alphabetical lists of the vascular plant families with their phylogenetic classification numbers. Colligo, 2(1) : 3- 10. https://perma.cc/2WFD-A2A7 KEY-WORDS Angiosperms family arrangement Summary: This paper provides, for herbarium cura- Gymnosperms Classification tors, the alphabetical lists of the recognized families Pteridophytes APG system in pteridophytes, gymnosperms and angiosperms Ferns PPG system with their phylogenetic classification numbers. Lycophytes phylogeny Herbarium MOTS-CLÉS Angiospermes rangement des familles Résumé : Cet article produit, pour les conservateurs Gymnospermes Classification d’herbier, les listes alphabétiques des familles recon- Ptéridophytes système APG nues pour les ptéridophytes, les gymnospermes et Fougères système PPG les angiospermes avec leurs numéros de classement Lycophytes phylogénie phylogénétique. Herbier Introduction These alphabetical lists have been established for the systems of A.-L de Jussieu, A.-P. de Can- The organization of herbarium collections con- dolle, Bentham & Hooker, etc. that are still used sists in arranging the specimens logically to in the management of historical herbaria find and reclassify them easily in the appro- whose original classification is voluntarily pre- priate storage units. In the vascular plant col- served. lections, commonly used methods are systema- Recent classification systems based on molecu- tic classification, alphabetical classification, or lar phylogenies have developed, and herbaria combinations of both.
    [Show full text]
  • Kuntheria Pedunculata (F.Muell.) Conran & Clifford Family: Colchicaceae Conran, J.G
    Australian Tropical Rainforest Plants - Online edition Kuntheria pedunculata (F.Muell.) Conran & Clifford Family: Colchicaceae Conran, J.G. & Clifford, H.T. (1987) Flora of Australia 45: 491. Stem Flowers and fruits as a multistemmed shrub about 1-2 m tall. Leaves Twigs zig-zagged. Leaves +/- distichous with about 5-7 main longitudinal veins including the midrib. Leaf blades about 6-18 x 2-6 cm, petioles about 0.1-0.5 cm long. Reticulate veins run +/- at right angles to the secondary veins like the rungs of a ladder. Petiole grooved or channelled on the upper surface. Flowers Tepals about 7-9 mm long. Stamens about 6-8 mm long, filaments about 3-4 mm long, anthers about 3-4 mm long. Each tepal folded around a stamen in the flower bud but opening to release them as Flowers. CC-BY J.L. Dowe the flower matures. Pollen yellow. Ovary about 3-4 mm diam., ovules numerous in each locule. Style about 1-2 mm long. Fruit Capsule 3-lobed, about 8-15 mm diam., styles persistent at the apex. Seeds white when fresh, about 7-9 x 4-6 mm, irregular in shape. Endosperm hard. Embryo very small, about 0.5 mm long, cylindrical. Seedlings Leaves and flowers. CC-BY J.L. Usually one cataphyll, bract-like, about 4-6 mm long. First pair of true leaves triplinerved. Leaf base Dowe clasping the stem at a point where it is distinctly bent. At the tenth leaf stage: leaf blade with about 5- 7 longitudinal veins on either side of the midrib.
    [Show full text]
  • Tracing History
    Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 911 Tracing History Phylogenetic, Taxonomic, and Biogeographic Research in the Colchicum Family BY ANNIKA VINNERSTEN ACTA UNIVERSITATIS UPSALIENSIS UPPSALA 2003 Dissertation presented at Uppsala University to be publicly examined in Lindahlsalen, EBC, Uppsala, Friday, December 12, 2003 at 10:00 for the degree of Doctor of Philosophy. The examination will be conducted in English. Abstract Vinnersten, A. 2003. Tracing History. Phylogenetic, Taxonomic and Biogeographic Research in the Colchicum Family. Acta Universitatis Upsaliensis. Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 911. 33 pp. Uppsala. ISBN 91-554-5814-9 This thesis concerns the history and the intrafamilial delimitations of the plant family Colchicaceae. A phylogeny of 73 taxa representing all genera of Colchicaceae, except the monotypic Kuntheria, is presented. The molecular analysis based on three plastid regions—the rps16 intron, the atpB- rbcL intergenic spacer, and the trnL-F region—reveal the intrafamilial classification to be in need of revision. The two tribes Iphigenieae and Uvularieae are demonstrated to be paraphyletic. The well-known genus Colchicum is shown to be nested within Androcymbium, Onixotis constitutes a grade between Neodregea and Wurmbea, and Gloriosa is intermixed with species of Littonia. Two new tribes are described, Burchardieae and Tripladenieae, and the two tribes Colchiceae and Uvularieae are emended, leaving four tribes in the family. At generic level new combinations are made in Wurmbea and Gloriosa in order to render them monophyletic. The genus Androcymbium is paraphyletic in relation to Colchicum and the latter genus is therefore expanded.
    [Show full text]
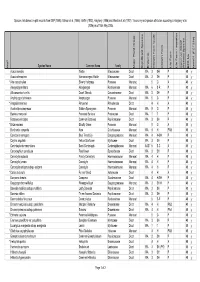
  • BFS048 Site Species List
    Species lists based on plot records from DEP (1996), Gibson et al. (1994), Griffin (1993), Keighery (1996) and Weston et al. (1992). Taxonomy and species attributes according to Keighery et al. (2006) as of 16th May 2005. Species Name Common Name Family Major Plant Group Significant Species Endemic Growth Form Code Growth Form Life Form Life Form - aquatics Common SSCP Wetland Species BFS No kens01 (FCT23a) Wd? Acacia sessilis Wattle Mimosaceae Dicot WA 3 SH P 48 y Acacia stenoptera Narrow-winged Wattle Mimosaceae Dicot WA 3 SH P 48 y * Aira caryophyllea Silvery Hairgrass Poaceae Monocot 5 G A 48 y Alexgeorgea nitens Alexgeorgea Restionaceae Monocot WA 6 S-R P 48 y Allocasuarina humilis Dwarf Sheoak Casuarinaceae Dicot WA 3 SH P 48 y Amphipogon turbinatus Amphipogon Poaceae Monocot WA 5 G P 48 y * Anagallis arvensis Pimpernel Primulaceae Dicot 4 H A 48 y Austrostipa compressa Golden Speargrass Poaceae Monocot WA 5 G P 48 y Banksia menziesii Firewood Banksia Proteaceae Dicot WA 1 T P 48 y Bossiaea eriocarpa Common Bossiaea Papilionaceae Dicot WA 3 SH P 48 y * Briza maxima Blowfly Grass Poaceae Monocot 5 G A 48 y Burchardia congesta Kara Colchicaceae Monocot WA 4 H PAB 48 y Calectasia narragara Blue Tinsel Lily Dasypogonaceae Monocot WA 4 H-SH P 48 y Calytrix angulata Yellow Starflower Myrtaceae Dicot WA 3 SH P 48 y Centrolepis drummondiana Sand Centrolepis Centrolepidaceae Monocot AUST 6 S-C A 48 y Conostephium pendulum Pearlflower Epacridaceae Dicot WA 3 SH P 48 y Conostylis aculeata Prickly Conostylis Haemodoraceae Monocot WA 4 H P 48 y Conostylis juncea Conostylis Haemodoraceae Monocot WA 4 H P 48 y Conostylis setigera subsp.
    [Show full text]
  • Gondwanan Origin of Major Monocot Groups Inferred from Dispersal-Vicariance Analysis Kåre Bremer Uppsala University
    Aliso: A Journal of Systematic and Evolutionary Botany Volume 22 | Issue 1 Article 3 2006 Gondwanan Origin of Major Monocot Groups Inferred from Dispersal-Vicariance Analysis Kåre Bremer Uppsala University Thomas Janssen Muséum National d'Histoire Naturelle Follow this and additional works at: http://scholarship.claremont.edu/aliso Part of the Botany Commons Recommended Citation Bremer, Kåre and Janssen, Thomas (2006) "Gondwanan Origin of Major Monocot Groups Inferred from Dispersal-Vicariance Analysis," Aliso: A Journal of Systematic and Evolutionary Botany: Vol. 22: Iss. 1, Article 3. Available at: http://scholarship.claremont.edu/aliso/vol22/iss1/3 Aliso 22, pp. 22-27 © 2006, Rancho Santa Ana Botanic Garden GONDWANAN ORIGIN OF MAJOR MONO COT GROUPS INFERRED FROM DISPERSAL-VICARIANCE ANALYSIS KARE BREMERl.3 AND THOMAS JANSSEN2 lDepartment of Systematic Botany, Evolutionary Biology Centre, Norbyvagen l8D, SE-752 36 Uppsala, Sweden; 2Museum National d'Histoire Naturelle, Departement de Systematique et Evolution, USM 0602: Taxonomie et collections, 16 rue Buffon, 75005 Paris, France 3Corresponding author ([email protected]) ABSTRACT Historical biogeography of major monocot groups was investigated by biogeographical analysis of a dated phylogeny including 79 of the 81 monocot families using the Angiosperm Phylogeny Group II (APG II) classification. Five major areas were used to describe the family distributions: Eurasia, North America, South America, Africa including Madagascar, and Australasia including New Guinea, New Caledonia, and New Zealand. In order to investigate the possible correspondence with continental breakup, the tree with its terminal distributions was fitted to the geological area cladogram «Eurasia, North America), (Africa, (South America, Australasia») and to alternative area cladograms using the TreeFitter program.
    [Show full text]
  • Biodiversity and Ecology of Critically Endangered, Rûens Silcrete Renosterveld in the Buffeljagsrivier Area, Swellendam
    Biodiversity and Ecology of Critically Endangered, Rûens Silcrete Renosterveld in the Buffeljagsrivier area, Swellendam by Johannes Philippus Groenewald Thesis presented in fulfilment of the requirements for the degree of Masters in Science in Conservation Ecology in the Faculty of AgriSciences at Stellenbosch University Supervisor: Prof. Michael J. Samways Co-supervisor: Dr. Ruan Veldtman December 2014 Stellenbosch University http://scholar.sun.ac.za Declaration I hereby declare that the work contained in this thesis, for the degree of Master of Science in Conservation Ecology, is my own work that have not been previously published in full or in part at any other University. All work that are not my own, are acknowledge in the thesis. ___________________ Date: ____________ Groenewald J.P. Copyright © 2014 Stellenbosch University All rights reserved ii Stellenbosch University http://scholar.sun.ac.za Acknowledgements Firstly I want to thank my supervisor Prof. M. J. Samways for his guidance and patience through the years and my co-supervisor Dr. R. Veldtman for his help the past few years. This project would not have been possible without the help of Prof. H. Geertsema, who helped me with the identification of the Lepidoptera and other insect caught in the study area. Also want to thank Dr. K. Oberlander for the help with the identification of the Oxalis species found in the study area and Flora Cameron from CREW with the identification of some of the special plants growing in the area. I further express my gratitude to Dr. Odette Curtis from the Overberg Renosterveld Project, who helped with the identification of the rare species found in the study area as well as information about grazing and burning of Renosterveld.
    [Show full text]
  • The Vascular System of Monocotyledonous Stems Author(S): Martin H
    The Vascular System of Monocotyledonous Stems Author(s): Martin H. Zimmermann and P. B. Tomlinson Source: Botanical Gazette, Vol. 133, No. 2 (Jun., 1972), pp. 141-155 Published by: The University of Chicago Press Stable URL: http://www.jstor.org/stable/2473813 . Accessed: 30/08/2011 15:50 Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at . http://www.jstor.org/page/info/about/policies/terms.jsp JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. The University of Chicago Press is collaborating with JSTOR to digitize, preserve and extend access to Botanical Gazette. http://www.jstor.org 1972] McCONNELL& STRUCKMEYER ALAR AND BORON-DEFICIENTTAGETES 141 tomato, turnip and cotton to variations in boron nutri- Further investigationson the relation of photoperiodto tion. II. Anatomical responses. BOT.GAZ. 118:53-71. the boron requirementsof plants. BOT.GAZ. 109:237-249. REED, D. J., T. C. MOORE, and J. D. ANDERSON. 1965. Plant WATANABE,R., W. CHORNEY,J. SKOK,and S. H. WENDER growth retardant B-995: a possible mode of action. 1964. Effect of boron deficiency on polyphenol produc- Science 148: 1469-1471. tion in the sunflower.Phytochemistry 3:391-393. SKOK, J. 1957. Relationships of boron nutrition to radio- ZEEVAART,J. A. D. 1966. Inhibition of stem growth and sensitivity of sunflower plants.
    [Show full text]
  • Evolutionary History of Floral Key Innovations in Angiosperms Elisabeth Reyes
    Evolutionary history of floral key innovations in angiosperms Elisabeth Reyes To cite this version: Elisabeth Reyes. Evolutionary history of floral key innovations in angiosperms. Botanics. Université Paris Saclay (COmUE), 2016. English. NNT : 2016SACLS489. tel-01443353 HAL Id: tel-01443353 https://tel.archives-ouvertes.fr/tel-01443353 Submitted on 23 Jan 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. NNT : 2016SACLS489 THESE DE DOCTORAT DE L’UNIVERSITE PARIS-SACLAY, préparée à l’Université Paris-Sud ÉCOLE DOCTORALE N° 567 Sciences du Végétal : du Gène à l’Ecosystème Spécialité de Doctorat : Biologie Par Mme Elisabeth Reyes Evolutionary history of floral key innovations in angiosperms Thèse présentée et soutenue à Orsay, le 13 décembre 2016 : Composition du Jury : M. Ronse de Craene, Louis Directeur de recherche aux Jardins Rapporteur Botaniques Royaux d’Édimbourg M. Forest, Félix Directeur de recherche aux Jardins Rapporteur Botaniques Royaux de Kew Mme. Damerval, Catherine Directrice de recherche au Moulon Président du jury M. Lowry, Porter Curateur en chef aux Jardins Examinateur Botaniques du Missouri M. Haevermans, Thomas Maître de conférences au MNHN Examinateur Mme. Nadot, Sophie Professeur à l’Université Paris-Sud Directeur de thèse M.
    [Show full text]