DOCSLIB.ORG

Evolutionary History of Floral Key Innovations in Angiosperms Elisabeth Reyes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Evolutionary History of Floral Key Innovations in Angiosperms Elisabeth Reyes Evolutionary history of floral key innovations in angiosperms Elisabeth Reyes To cite this version: Elisabeth Reyes. Evolutionary history of floral key innovations in angiosperms. Botanics. Université Paris Saclay (COmUE), 2016. English. NNT : 2016SACLS489. tel-01443353 HAL Id: tel-01443353 https://tel.archives-ouvertes.fr/tel-01443353 Submitted on 23 Jan 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. NNT : 2016SACLS489 THESE DE DOCTORAT DE L’UNIVERSITE PARIS-SACLAY, préparée à l’Université Paris-Sud ÉCOLE DOCTORALE N° 567 Sciences du Végétal : du Gène à l’Ecosystème Spécialité de Doctorat : Biologie Par Mme Elisabeth Reyes Evolutionary history of floral key innovations in angiosperms Thèse présentée et soutenue à Orsay, le 13 décembre 2016 : Composition du Jury : M. Ronse de Craene, Louis Directeur de recherche aux Jardins Rapporteur Botaniques Royaux d’Édimbourg M. Forest, Félix Directeur de recherche aux Jardins Rapporteur Botaniques Royaux de Kew Mme. Damerval, Catherine Directrice de recherche au Moulon Président du jury M. Lowry, Porter Curateur en chef aux Jardins Examinateur Botaniques du Missouri M. Haevermans, Thomas Maître de conférences au MNHN Examinateur Mme. Nadot, Sophie Professeur à l’Université Paris-Sud Directeur de thèse M. Sauquet, Hervé Maître de conférences à l’Université Invité (co-directeur de Paris-Sud thèse) ACKNOWLEDGEMENTS I thank my thesis supervisors Sophie and Hervé for their help, as well as the other members of the EVA team, but most particularly the people I saw regularly such as Julien, Frank, Stefan, Laetitia, Renske, Qian, Charlotte, James, Véronique and Thierry. I also thank people from outside the team that have contributed to my papers such as Hélène Morlon, Jürg Schönenberger and Maria von Balthazar. I thank the jury Louis Ronse de Craene, Félix Forest, Catherine Damerval, Porter Lowry, and Thomas Haevermans to have taken time to evaluate my thesis and participate in the defense. I thank the member of my thesis committee for advising me: Susana Magallón, Marianne Elias, Jean-Yves Dubuisson. I also thank Jacqui and Martine for having helped me with my various paperwork worries and the other people I got to meet during my stay in this lab. I thank my parents and officemates Roxane, Julie and Angeline for their moral support. 2 TABLE OF CONTENTS ACKNOWLEDGEMENTS ..................................................................................................... 2 TABLE OF CONTENTS ......................................................................................................... 3 GENERAL INTRODUCTION ............................................................................................... 4 1. The many faces of the flower ................................................................................................................... 4 2. A series of abominable mysteries ............................................................................................................ 6 3. The neglected flip side of the abominable mystery.................................................................................. 9 4. The critical role of ancestral state reconstruction in the study of character evolution ........................... 10 5. Thesis objectives .................................................................................................................................... 11 CHAPTER 1: Presence in Mediterranean hotspots and floral symmetry affect speciation and extinction rates in Proteaceae ........................................................................................ 13 ABSTRACT .............................................................................................................................................. 18 INTRODUCTION ..................................................................................................................................... 19 MATERIALS AND METHODS ............................................................................................................... 22 RESULTS .................................................................................................................................................. 26 DISCUSSION ............................................................................................................................................ 30 ACKNOWLEDGEMENTS ....................................................................................................................... 37 CHAPTER 2: Perianth symmetry changed at least 199 times in angiosperm evolution 38 ABSTRACT .............................................................................................................................................. 42 INTRODUCTION ..................................................................................................................................... 43 MATERIALS AND METHODS ............................................................................................................... 44 RESULTS .................................................................................................................................................. 47 DISCUSSION ............................................................................................................................................ 57 ACKNOWLEDGMENTS ......................................................................................................................... 71 CHAPTER 3: Does heterogeneity of rates of morphological evolution affect ancestral state reconstructions? An empirical test with five floral characters ................................. 72 ABSTRACT .............................................................................................................................................. 76 INTRODUCTION ..................................................................................................................................... 77 MATERIALS AND METHODS ............................................................................................................... 79 RESULTS .................................................................................................................................................. 84 DISCUSSION ............................................................................................................................................ 90 GENERAL DISCUSSION ................................................................................................... 100 Properties of trees created by “change-capturing” transitions in binary characters ................................. 101 Elements missing to better understand the diversification of angiosperms ............................................. 106 CONCLUSION AND PERSPECTIVES ............................................................................ 112 LITERATURE CITED ........................................................................................................ 115 SUPPORTING INFORMATION ....................................................................................... 130 3 GENERAL INTRODUCTION 1. THE MANY FACES OF THE FLOWER The flower is a short axis bearing, from the center out, female reproductive organs consisting of ovules protected by carpels, male reproductive organs called stamens and a perianth (Bateman et al. 2006). The flower is one of the most distinctive features of angiosperms, the clade of land plants with the highest diversity. “Diversity” is here used in the sense of having a large number of species, and is accompanied by a variety of flower forms that is exemplified in Figure I.1. The image that the word “flower” evokes to the layman probably greatly resembles the upper left picture of Figure I.1 and consists of reproductive organs of both sexes surrounded by a specialized two-whorl perianth in which the inner whorl is colorful and showy but delicate, while the outer whorl is more inconspicuous and stiff as it protects the developing bud; it will also probably have five petals and five sepals. That mental picture includes the organs being separate and those of a given category being the same size and shape. Adaptation to pollinators, self-pollination, abiotic pollination or simply evolutionary history has led to the development among flowers of aspects that are radically different from that “layman’s mental image”. For instance, the “sepal and petal” perianth is not the only form of perianth that exists and is actually a derived state (see Figure I.3 and Chapter 3). Species from the early-diverging clades of angiosperms can have only one type of perianth part, or two types that are different in shape but of similar color, petal-like or sepal-like. Flowers from these early- diverging clades can also have more than two perianth whorls or a spiral perianth, usually associated with a large number of perianth parts. While most species in such cases are found in early-diverging angiosperms, the above situations occasionally appear within clades in which the “sepal and
Load more

Recommended publications
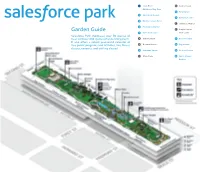
  • Salesforce Park Garden Guide
    Start Here! D Central Lawn Children’s Play Area Garden Guide6 Palm Garden 1 Australian Garden Start Here! D Central Lawn Salesforce Park showcases7 California over Garden 50 species of Children’s Play Area 2 Mediterraneantrees and Basin over 230 species of understory plants. 6 Palm Garden -ã ¼ÜÊ ÊăØÜ ØÊèÜãE úØƀØÊèÃJapanese Maples ¼ÃØ Ê¢ 1 Australian Garden 3 Prehistoric¢ØÕ輫ÕØÊ£ØÂÜÃã«ó«ã«Üŧ¼«¹ĆãÃÜÜ Garden 7 California Garden ¼ÜÜÜŧÊÃØãÜŧÃØ¢ã«Ã£¼ÜÜÜũF Amphitheater Garden Guide 2 Mediterranean Basin 4 Wetland Garden Main Lawn E Japanese Maples Salesforce Park showcases over 50 species of 3 Prehistoric Garden trees and over 230 species of understory plants. A Oak Meadow 8 Desert Garden F Amphitheater It also offers a robust year-round calendar of 4 Wetland Garden Main Lawn free public programs and activities, like fitness B Bamboo Grove 9 Fog Garden Desert Garden classes, concerts, and crafting classes! A Oak Meadow 8 5 Redwood Forest 10 Chilean Garden B Bamboo Grove 9 Fog Garden C Main Plaza 11 South African 10 Chilean Garden Garden 5 Redwood Forest C Main Plaza 11 South African Garden 1 Children’s Australian Play Area Garden ABOUT THE GARDENS The botanist aboard the Endeavor, Sir Joseph Banks, is credited with introducing many plants from Australia to the western world, and many This 5.4 acre park has a layered soil system that plants today bear his name. balances seismic shifting, collects and filters storm- water, and irrigates the gardens. Additionally, the soil Native to eastern Australia, Grass Trees may grow build-up and dense planting help offset the urban only 3 feet in 100 years, and mature plants can be heat island effect by lowering the air temperature.
    [Show full text]
  • Towards an Understanding of the Evolution of Violaceae from an Anatomical and Morphological Perspective Saul Ernesto Hoyos University of Missouri-St
    University of Missouri, St. Louis IRL @ UMSL Theses Graduate Works 8-7-2011 Towards an understanding of the evolution of Violaceae from an anatomical and morphological perspective Saul Ernesto Hoyos University of Missouri-St. Louis, [email protected] Follow this and additional works at: http://irl.umsl.edu/thesis Recommended Citation Hoyos, Saul Ernesto, "Towards an understanding of the evolution of Violaceae from an anatomical and morphological perspective" (2011). Theses. 50. http://irl.umsl.edu/thesis/50 This Thesis is brought to you for free and open access by the Graduate Works at IRL @ UMSL. It has been accepted for inclusion in Theses by an authorized administrator of IRL @ UMSL. For more information, please contact [email protected]. Saul E. Hoyos Gomez MSc. Ecology, Evolution and Systematics, University of Missouri-Saint Louis, 2011 Thesis Submitted to The Graduate School at the University of Missouri – St. Louis in partial fulfillment of the requirements for the degree Master of Science July 2011 Advisory Committee Peter Stevens, Ph.D. Chairperson Peter Jorgensen, Ph.D. Richard Keating, Ph.D. TOWARDS AN UNDERSTANDING OF THE BASAL EVOLUTION OF VIOLACEAE FROM AN ANATOMICAL AND MORPHOLOGICAL PERSPECTIVE Saul Hoyos Introduction The violet family, Violaceae, are predominantly tropical and contains 23 genera and upwards of 900 species (Feng 2005, Tukuoka 2008, Wahlert and Ballard 2010 in press). The family is monophyletic (Feng 2005, Tukuoka 2008, Wahlert & Ballard 2010 in press), even though phylogenetic relationships within Violaceae are still unclear (Feng 2005, Tukuoka 2008). The family embrace a great diversity of vegetative and floral morphologies. Members are herbs, lianas or trees, with flowers ranging from strongly spurred to unspurred.
    [Show full text]
  • The Species of Alseuosmia (Alseuosmiaceae)
    New Zealand Journal of Botany, 1978, Vol. 16: 271-7. 271 The species of Alseuosmia (Alseuosmiaceae) RHYS O. GARDNER Department of Botany, University of Auckland, Private Bag, Auckland, New Zealand (Received 15 September 1977) ABSTRACT A new species Alseuosmia turneri R. 0. Gardner (Alseuosmiaceae Airy Shaw) from the Volcanic Plateau, North Island, New Zealand is described and illustrated. A. linariifolia A. Cunn. is reduced to a variety of A. banksii A. Cunn. and A. quercifolia A. Cunn. is given hybrid status (=^4. banksii A. Cunn. x A. macrophylla A. Cunn.). A key to the four Alseuosmia species, synonymy, and a generalised distribution map are given. A. pusilla Col. is illustrated for the first time. INTRODUCTION judged to be frequent between only one pair of Allan Cunningham (1839) described eight species and the "excessive variability" lies mostly species of a new flowering plant genus Alseuosmia there. from material collected in the Bay of Islands region by Banks and Solander in 1769, by himself in 1826 and 1838, and by his brother Richard in 1833-4. The A NEW SPECIES OF ALSEUOSMIA species, all shrubs of the lowland forest, were sup- A. CUNN. posed to differ from one another chiefly in the shape and toothing of their leaves. An undescribed species of Alseuosmia from the Hooker (1852-5, 1864), with the benefit of Waimarino region of the Volcanic Plateau has been additional Colenso and Sinclair material, reduced known for some time (Cockayne 1928, p. 179; A. P. Cunningham's species to four, but stated that these Druce in Atkinson 1971). The following description four species were "excessively variable".
    [Show full text]
  • Interim Recovery Plan No
    INTERIM RECOVERY PLAN NO. 202 ALBANY WOOLLYBUSH (ADENANTHOS x CUNNINGHAMII) INTERIM RECOVERY PLAN 2005-2010 Sandra Gilfillan1, Sarah Barrett2 and Renée Hartley3 1 Conservation Officer, CALM Albany Region, 120 Albany Hwy, Albany 6330. 2 Flora Conservation Officer, CALM Albany Work Centre, 120 Albany Hwy, Albany 6330 3 Technical Officer, CALM Albany Work Centre, 120 Albany Hwy, Albany 6330 Photo: Ellen Hickman April 2005 Department of Conservation and Land Management Albany Work Centre, South Coast Region, 120 Albany Hwy, Albany WA 6331 Interim Recovery Plan for Adenanthos x cunninghammi FOREWORD Interim Recovery Plans (IRPs) are developed within the framework laid down in Department of Conservation and Land Management (CALM) Policy Statements Nos. 44 and 50. IRPs outline the recovery actions that are required to urgently address those threatening processes most affecting the ongoing survival of threatened taxa or ecological communities, and begin the recovery process. CALM is committed to ensuring that Threatened taxa are conserved through the preparation and implementation of Recovery Plans (RPs) or IRPs and by ensuring that conservation action commences as soon as possible. This IRP will operate from April 2005 to March 2010 but will remain in force until withdrawn or replaced. It is intended that, if the taxon is still ranked Endangered, this IRP will be reviewed after five years and the need further recovery actions assessed. This IRP was given regional approval on 26 October, 2005 and was approved by the Director of Nature Conservation on 26 October, 2005. The provision of funds and personnel identified in this IRP is dependent on budgetary and other constraints affecting CALM, as well as the need to address other priorities.
    [Show full text]
  • Outline of Angiosperm Phylogeny
    Outline of angiosperm phylogeny: orders, families, and representative genera with emphasis on Oregon native plants Priscilla Spears December 2013 The following listing gives an introduction to the phylogenetic classification of the flowering plants that has emerged in recent decades, and which is based on nucleic acid sequences as well as morphological and developmental data. This listing emphasizes temperate families of the Northern Hemisphere and is meant as an overview with examples of Oregon native plants. It includes many exotic genera that are grown in Oregon as ornamentals plus other plants of interest worldwide. The genera that are Oregon natives are printed in a blue font. Genera that are exotics are shown in black, however genera in blue may also contain non-native species. Names separated by a slash are alternatives or else the nomenclature is in flux. When several genera have the same common name, the names are separated by commas. The order of the family names is from the linear listing of families in the APG III report. For further information, see the references on the last page. Basal Angiosperms (ANITA grade) Amborellales Amborellaceae, sole family, the earliest branch of flowering plants, a shrub native to New Caledonia – Amborella Nymphaeales Hydatellaceae – aquatics from Australasia, previously classified as a grass Cabombaceae (water shield – Brasenia, fanwort – Cabomba) Nymphaeaceae (water lilies – Nymphaea; pond lilies – Nuphar) Austrobaileyales Schisandraceae (wild sarsaparilla, star vine – Schisandra; Japanese
    [Show full text]
  • Alphabetical Lists of the Vascular Plant Families with Their Phylogenetic
    Colligo 2 (1) : 3-10 BOTANIQUE Alphabetical lists of the vascular plant families with their phylogenetic classification numbers Listes alphabétiques des familles de plantes vasculaires avec leurs numéros de classement phylogénétique FRÉDÉRIC DANET* *Mairie de Lyon, Espaces verts, Jardin botanique, Herbier, 69205 Lyon cedex 01, France - [email protected] Citation : Danet F., 2019. Alphabetical lists of the vascular plant families with their phylogenetic classification numbers. Colligo, 2(1) : 3- 10. https://perma.cc/2WFD-A2A7 KEY-WORDS Angiosperms family arrangement Summary: This paper provides, for herbarium cura- Gymnosperms Classification tors, the alphabetical lists of the recognized families Pteridophytes APG system in pteridophytes, gymnosperms and angiosperms Ferns PPG system with their phylogenetic classification numbers. Lycophytes phylogeny Herbarium MOTS-CLÉS Angiospermes rangement des familles Résumé : Cet article produit, pour les conservateurs Gymnospermes Classification d’herbier, les listes alphabétiques des familles recon- Ptéridophytes système APG nues pour les ptéridophytes, les gymnospermes et Fougères système PPG les angiospermes avec leurs numéros de classement Lycophytes phylogénie phylogénétique. Herbier Introduction These alphabetical lists have been established for the systems of A.-L de Jussieu, A.-P. de Can- The organization of herbarium collections con- dolle, Bentham & Hooker, etc. that are still used sists in arranging the specimens logically to in the management of historical herbaria find and reclassify them easily in the appro- whose original classification is voluntarily pre- priate storage units. In the vascular plant col- served. lections, commonly used methods are systema- Recent classification systems based on molecu- tic classification, alphabetical classification, or lar phylogenies have developed, and herbaria combinations of both.
    [Show full text]
  • Complete Chloroplast Genomes Shed Light on Phylogenetic
    www.nature.com/scientificreports OPEN Complete chloroplast genomes shed light on phylogenetic relationships, divergence time, and biogeography of Allioideae (Amaryllidaceae) Ju Namgung1,4, Hoang Dang Khoa Do1,2,4, Changkyun Kim1, Hyeok Jae Choi3 & Joo‑Hwan Kim1* Allioideae includes economically important bulb crops such as garlic, onion, leeks, and some ornamental plants in Amaryllidaceae. Here, we reported the complete chloroplast genome (cpDNA) sequences of 17 species of Allioideae, fve of Amaryllidoideae, and one of Agapanthoideae. These cpDNA sequences represent 80 protein‑coding, 30 tRNA, and four rRNA genes, and range from 151,808 to 159,998 bp in length. Loss and pseudogenization of multiple genes (i.e., rps2, infA, and rpl22) appear to have occurred multiple times during the evolution of Alloideae. Additionally, eight mutation hotspots, including rps15-ycf1, rps16-trnQ-UUG, petG-trnW-CCA , psbA upstream, rpl32- trnL-UAG , ycf1, rpl22, matK, and ndhF, were identifed in the studied Allium species. Additionally, we present the frst phylogenomic analysis among the four tribes of Allioideae based on 74 cpDNA coding regions of 21 species of Allioideae, fve species of Amaryllidoideae, one species of Agapanthoideae, and fve species representing selected members of Asparagales. Our molecular phylogenomic results strongly support the monophyly of Allioideae, which is sister to Amaryllioideae. Within Allioideae, Tulbaghieae was sister to Gilliesieae‑Leucocoryneae whereas Allieae was sister to the clade of Tulbaghieae‑ Gilliesieae‑Leucocoryneae. Molecular dating analyses revealed the crown age of Allioideae in the Eocene (40.1 mya) followed by diferentiation of Allieae in the early Miocene (21.3 mya). The split of Gilliesieae from Leucocoryneae was estimated at 16.5 mya.
    [Show full text]
  • Bio 308-Course Guide
    COURSE GUIDE BIO 308 BIOGEOGRAPHY Course Team Dr. Kelechi L. Njoku (Course Developer/Writer) Professor A. Adebanjo (Programme Leader)- NOUN Abiodun E. Adams (Course Coordinator)-NOUN NATIONAL OPEN UNIVERSITY OF NIGERIA BIO 308 COURSE GUIDE National Open University of Nigeria Headquarters 14/16 Ahmadu Bello Way Victoria Island Lagos Abuja Office No. 5 Dar es Salaam Street Off Aminu Kano Crescent Wuse II, Abuja e-mail: [email protected] URL: www.nou.edu.ng Published by National Open University of Nigeria Printed 2013 ISBN: 978-058-434-X All Rights Reserved Printed by: ii BIO 308 COURSE GUIDE CONTENTS PAGE Introduction ……………………………………......................... iv What you will Learn from this Course …………………............ iv Course Aims ……………………………………………............ iv Course Objectives …………………………………………....... iv Working through this Course …………………………….......... v Course Materials ………………………………………….......... v Study Units ………………………………………………......... v Textbooks and References ………………………………........... vi Assessment ……………………………………………….......... vi End of Course Examination and Grading..................................... vi Course Marking Scheme................................................................ vii Presentation Schedule.................................................................... vii Tutor-Marked Assignment ……………………………….......... vii Tutors and Tutorials....................................................................... viii iii BIO 308 COURSE GUIDE INTRODUCTION BIO 308: Biogeography is a one-semester, 2 credit- hour course in Biology. It is a 300 level, second semester undergraduate course offered to students admitted in the School of Science and Technology, School of Education who are offering Biology or related programmes. The course guide tells you briefly what the course is all about, what course materials you will be using and how you can work your way through these materials. It gives you some guidance on your Tutor- Marked Assignments. There are Self-Assessment Exercises within the body of a unit and/or at the end of each unit.
    [Show full text]
  • South American Cacti in Time and Space: Studies on the Diversification of the Tribe Cereeae, with Particular Focus on Subtribe Trichocereinae (Cactaceae)
    Zurich Open Repository and Archive University of Zurich Main Library Strickhofstrasse 39 CH-8057 Zurich www.zora.uzh.ch Year: 2013 South American Cacti in time and space: studies on the diversification of the tribe Cereeae, with particular focus on subtribe Trichocereinae (Cactaceae) Lendel, Anita Posted at the Zurich Open Repository and Archive, University of Zurich ZORA URL: https://doi.org/10.5167/uzh-93287 Dissertation Published Version Originally published at: Lendel, Anita. South American Cacti in time and space: studies on the diversification of the tribe Cereeae, with particular focus on subtribe Trichocereinae (Cactaceae). 2013, University of Zurich, Faculty of Science. South American Cacti in Time and Space: Studies on the Diversification of the Tribe Cereeae, with Particular Focus on Subtribe Trichocereinae (Cactaceae) _________________________________________________________________________________ Dissertation zur Erlangung der naturwissenschaftlichen Doktorwürde (Dr.sc.nat.) vorgelegt der Mathematisch-naturwissenschaftlichen Fakultät der Universität Zürich von Anita Lendel aus Kroatien Promotionskomitee: Prof. Dr. H. Peter Linder (Vorsitz) PD. Dr. Reto Nyffeler Prof. Dr. Elena Conti Zürich, 2013 Table of Contents Acknowledgments 1 Introduction 3 Chapter 1. Phylogenetics and taxonomy of the tribe Cereeae s.l., with particular focus 15 on the subtribe Trichocereinae (Cactaceae – Cactoideae) Chapter 2. Floral evolution in the South American tribe Cereeae s.l. (Cactaceae: 53 Cactoideae): Pollination syndromes in a comparative phylogenetic context Chapter 3. Contemporaneous and recent radiations of the world’s major succulent 86 plant lineages Chapter 4. Tackling the molecular dating paradox: underestimated pitfalls and best 121 strategies when fossils are scarce Outlook and Future Research 207 Curriculum Vitae 209 Summary 211 Zusammenfassung 213 Acknowledgments I really believe that no one can go through the process of doing a PhD and come out without being changed at a very profound level.
    [Show full text]
  • Biogeography and Diversification of Brassicales
    Molecular Phylogenetics and Evolution 99 (2016) 204–224 Contents lists available at ScienceDirect Molecular Phylogenetics and Evolution journal homepage: www.elsevier.com/locate/ympev Biogeography and diversification of Brassicales: A 103 million year tale ⇑ Warren M. Cardinal-McTeague a,1, Kenneth J. Sytsma b, Jocelyn C. Hall a, a Department of Biological Sciences, University of Alberta, Edmonton, Alberta T6G 2E9, Canada b Department of Botany, University of Wisconsin, Madison, WI 53706, USA article info abstract Article history: Brassicales is a diverse order perhaps most famous because it houses Brassicaceae and, its premier mem- Received 22 July 2015 ber, Arabidopsis thaliana. This widely distributed and species-rich lineage has been overlooked as a Revised 24 February 2016 promising system to investigate patterns of disjunct distributions and diversification rates. We analyzed Accepted 25 February 2016 plastid and mitochondrial sequence data from five gene regions (>8000 bp) across 151 taxa to: (1) Available online 15 March 2016 produce a chronogram for major lineages in Brassicales, including Brassicaceae and Arabidopsis, based on greater taxon sampling across the order and previously overlooked fossil evidence, (2) examine Keywords: biogeographical ancestral range estimations and disjunct distributions in BioGeoBEARS, and (3) determine Arabidopsis thaliana where shifts in species diversification occur using BAMM. The evolution and radiation of the Brassicales BAMM BEAST began 103 Mya and was linked to a series of inter-continental vicariant, long-distance dispersal, and land BioGeoBEARS bridge migration events. North America appears to be a significant area for early stem lineages in the Brassicaceae order. Shifts to Australia then African are evident at nodes near the core Brassicales, which diverged Cleomaceae 68.5 Mya (HPD = 75.6–62.0).
    [Show full text]
  • Adenanthos Pungens Subsp. Effusus)
    SPRAWLING SPIKY ADENANTHOS (ADENANTHOS PUNGENS SUBSP. EFFUSUS) RECOVERY PLAN Department of Environment and Conservation Kensington Recovery Plan for Adenanthos pungens subsp. effusus FOREWORD Interim Recovery Plans (IRPs) are developed within the framework laid down in WA Department of Conservation and Land Management (CALM), now Department of Environment and Conservation (DEC) Policy Statements Nos. 44 and 50. Note: the Department of CALM formally became the Department of Environment and Conservation (DEC) in July 2006. DEC will continue to adhere to these Policy Statements until they are revised and reissued. IRPs outline the recovery actions that are required to urgently address those threatening processes most affecting the ongoing survival of threatened taxa or ecological communities, and begin the recovery process. DEC is committed to ensuring that Threatened taxa are conserved through the preparation and implementation of Recovery Plans (RPs) or IRPs, and by ensuring that conservation action commences as soon as possible and, in the case of Critically Endangered (CR) taxa, always within one year of endorsement of that rank by the Minister. This IRP results from a review of, and replaces, IRP No. 78 Adenanthos pungens subsp. effusus (Evans, Stack, Loudon, Graham and Brown 2000). This Interim Recovery Plan will operate from May 2006 to April 2011 but will remain in force until withdrawn or replaced. It is intended that, if the taxon is still ranked as Critically Endangered (WA), this IRP will be reviewed after five years and the need for a full Recovery Plan will be assessed. This IRP was given regional approval on 13 February, 2006 and was approved by the Director of Nature Conservation on 22 February, 2006.
    [Show full text]
  • Flora Mediterranea 26
    FLORA MEDITERRANEA 26 Published under the auspices of OPTIMA by the Herbarium Mediterraneum Panormitanum Palermo – 2016 FLORA MEDITERRANEA Edited on behalf of the International Foundation pro Herbario Mediterraneo by Francesco M. Raimondo, Werner Greuter & Gianniantonio Domina Editorial board G. Domina (Palermo), F. Garbari (Pisa), W. Greuter (Berlin), S. L. Jury (Reading), G. Kamari (Patras), P. Mazzola (Palermo), S. Pignatti (Roma), F. M. Raimondo (Palermo), C. Salmeri (Palermo), B. Valdés (Sevilla), G. Venturella (Palermo). Advisory Committee P. V. Arrigoni (Firenze) P. Küpfer (Neuchatel) H. M. Burdet (Genève) J. Mathez (Montpellier) A. Carapezza (Palermo) G. Moggi (Firenze) C. D. K. Cook (Zurich) E. Nardi (Firenze) R. Courtecuisse (Lille) P. L. Nimis (Trieste) V. Demoulin (Liège) D. Phitos (Patras) F. Ehrendorfer (Wien) L. Poldini (Trieste) M. Erben (Munchen) R. M. Ros Espín (Murcia) G. Giaccone (Catania) A. Strid (Copenhagen) V. H. Heywood (Reading) B. Zimmer (Berlin) Editorial Office Editorial assistance: A. M. Mannino Editorial secretariat: V. Spadaro & P. Campisi Layout & Tecnical editing: E. Di Gristina & F. La Sorte Design: V. Magro & L. C. Raimondo Redazione di "Flora Mediterranea" Herbarium Mediterraneum Panormitanum, Università di Palermo Via Lincoln, 2 I-90133 Palermo, Italy [email protected] Printed by Luxograph s.r.l., Piazza Bartolomeo da Messina, 2/E - Palermo Registration at Tribunale di Palermo, no. 27 of 12 July 1991 ISSN: 1120-4052 printed, 2240-4538 online DOI: 10.7320/FlMedit26.001 Copyright © by International Foundation pro Herbario Mediterraneo, Palermo Contents V. Hugonnot & L. Chavoutier: A modern record of one of the rarest European mosses, Ptychomitrium incurvum (Ptychomitriaceae), in Eastern Pyrenees, France . 5 P. Chène, M.
    [Show full text]