Harnessing Speckle for a Sub-Femtometre Resolved Broadband Wavemeter and Laser Stabilization
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

CAR-ANS Part 5 Governing Units of Measurement to Be Used in Air and Ground Operations
CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES Part 5 Governing UNITS OF MEASUREMENT TO BE USED IN AIR AND GROUND OPERATIONS CIVIL AVIATION AUTHORITY OF THE PHILIPPINES Old MIA Road, Pasay City1301 Metro Manila UNCOTROLLED COPY INTENTIONALLY LEFT BLANK UNCOTROLLED COPY CAR-ANS PART 5 Republic of the Philippines CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES (CAR-ANS) Part 5 UNITS OF MEASUREMENTS TO BE USED IN AIR AND GROUND OPERATIONS 22 APRIL 2016 EFFECTIVITY Part 5 of the Civil Aviation Regulations-Air Navigation Services are issued under the authority of Republic Act 9497 and shall take effect upon approval of the Board of Directors of the CAAP. APPROVED BY: LT GEN WILLIAM K HOTCHKISS III AFP (RET) DATE Director General Civil Aviation Authority of the Philippines Issue 2 15-i 16 May 2016 UNCOTROLLED COPY CAR-ANS PART 5 FOREWORD This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was formulated and issued by the Civil Aviation Authority of the Philippines (CAAP), prescribing the standards and recommended practices for units of measurements to be used in air and ground operations within the territory of the Republic of the Philippines. This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was developed based on the Standards and Recommended Practices prescribed by the International Civil Aviation Organization (ICAO) as contained in Annex 5 which was first adopted by the council on 16 April 1948 pursuant to the provisions of Article 37 of the Convention of International Civil Aviation (Chicago 1944), and consequently became applicable on 1 January 1949. The provisions contained herein are issued by authority of the Director General of the Civil Aviation Authority of the Philippines and will be complied with by all concerned. -

Orders of Magnitude (Length) - Wikipedia
03/08/2018 Orders of magnitude (length) - Wikipedia Orders of magnitude (length) The following are examples of orders of magnitude for different lengths. Contents Overview Detailed list Subatomic Atomic to cellular Cellular to human scale Human to astronomical scale Astronomical less than 10 yoctometres 10 yoctometres 100 yoctometres 1 zeptometre 10 zeptometres 100 zeptometres 1 attometre 10 attometres 100 attometres 1 femtometre 10 femtometres 100 femtometres 1 picometre 10 picometres 100 picometres 1 nanometre 10 nanometres 100 nanometres 1 micrometre 10 micrometres 100 micrometres 1 millimetre 1 centimetre 1 decimetre Conversions Wavelengths Human-defined scales and structures Nature Astronomical 1 metre Conversions https://en.wikipedia.org/wiki/Orders_of_magnitude_(length) 1/44 03/08/2018 Orders of magnitude (length) - Wikipedia Human-defined scales and structures Sports Nature Astronomical 1 decametre Conversions Human-defined scales and structures Sports Nature Astronomical 1 hectometre Conversions Human-defined scales and structures Sports Nature Astronomical 1 kilometre Conversions Human-defined scales and structures Geographical Astronomical 10 kilometres Conversions Sports Human-defined scales and structures Geographical Astronomical 100 kilometres Conversions Human-defined scales and structures Geographical Astronomical 1 megametre Conversions Human-defined scales and structures Sports Geographical Astronomical 10 megametres Conversions Human-defined scales and structures Geographical Astronomical 100 megametres 1 gigametre -

Metrication Leaders Guide 2009
Metrication Leaders Guide This resource book will help make your inevitable upgrade to the metric system easy, smooth, cheap, and fast. Pat Naughtin 2009 2 of 89 Make your upgrade to the metric system easy, smooth, cheap, and fast Decision making for metrication leaders !! " ! # $ Appendices % & % ! !! ' ! ( )% ' !* " " + , -&..)--/& , - ,$ # ! ,, 0 * + # ( http://metricationmatters.com [email protected] 3 of 89 Make your upgrade to the metric system easy, smooth, cheap, and fast. Deciding on a metrication program confirms that you are a metrication leader – not a follower. You have the courage to stand aside from the crowd, decide what you think is best for yourself and for others, and you are prepared to differ from other people in your class, your work group, your company, or your industry. As a metrication leader, you will soon discover three things: 1 Metrication is technically a simple process. 2 Metrication doesn't take long if you pursue a planned and timed program. 3 Metrication can provoke deeply felt anti-metrication emotions in people who have had no measurement experience with metric measures, or people who have difficulty with change. The first two encourage confidence – it's simple and it won't take long – but the third factor can give you an intense feeling of isolation when you first begin your metrication program. You feel you are learning a new language (you are – a new measuring language), while people around you not only refuse to learn this language, but will do what they can to prevent you from growing and from making progressive developments in your life. The purpose of this book is to give you some supporting arguments to use in your metrication process. -

6411 Measure Unit Qualifier Indication of the Unit of Measurement in Which Weight (Mass), Capacity, Length, Area, Volume Or Other Quantity Is Expressed
Code list 6411 Standard: UN D.96B S3 6411 Measure unit qualifier Indication of the unit of measurement in which weight (mass), capacity, length, area, volume or other quantity is expressed. Note: See UN/ECE Recommendation 20. 04 small spray 05 lift 08 heat lot 10 group 11 outfit 13 ration 14 shot 15 stick 16 hundred fifteen kg drum 17 hundred lb drum 18 fiftyfive gallon (US) drum 19 tank truck 20 twenty foot container 21 forty foot container 22 decilitre per gram 23 gram per cubic centimetre 24 theoretical pound 25 gram per square centimetre 26 actual ton 27 theoretical ton 28 kilogram per square metre 29 pound per thousand square feet 30 horse power day per air dry metric ton 31 catch weight 32 kilogram per air dry metric ton 33 kilopascal square metres per gram 34 kilopascals per millimetre 35 millilitres per square centimetre second 36 cubic feet per minute per square foot 37 ounce per square foot 38 ounces per square foot per 0,01 inch 40 millilitre per second 41 millilitre per minute 43 super bulk bag 44 fivehundred kg bulk bag 45 threehundred kg bulk bag 46 fifty lb bulk bag 47 fifty lb bag 48 bulk car load 53 theoretical kilograms Printed by GEFEG EDIFIX® Print date: 26/09/2001 Page: 1 Code list 6411 Standard: UN D.96B S3 54 theoretical tonne 56 sitas 57 mesh 58 net kilogram 59 part per million 60 percent weight 61 part per billion (US) 62 percent per 1000 hour 63 failure rate in time 64 pound per square inch, gauge 66 oersted 69 test specific scale 71 volt ampere per pound 72 watt per pound 73 ampere tum per centimetre 74 millipascal -
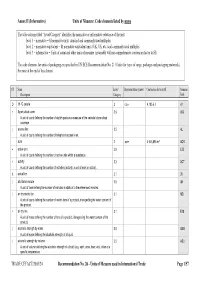
Units of Measure Used in International Trade Page 1/57 Annex II (Informative) Units of Measure: Code Elements Listed by Name
Annex II (Informative) Units of Measure: Code elements listed by name The table column titled “Level/Category” identifies the normative or informative relevance of the unit: level 1 – normative = SI normative units, standard and commonly used multiples level 2 – normative equivalent = SI normative equivalent units (UK, US, etc.) and commonly used multiples level 3 – informative = Units of count and other units of measure (invariably with no comprehensive conversion factor to SI) The code elements for units of packaging are specified in UN/ECE Recommendation No. 21 (Codes for types of cargo, packages and packaging materials). See note at the end of this Annex). ST Name Level/ Representation symbol Conversion factor to SI Common Description Category Code D 15 °C calorie 2 cal₁₅ 4,185 5 J A1 + 8-part cloud cover 3.9 A59 A unit of count defining the number of eighth-parts as a measure of the celestial dome cloud coverage. | access line 3.5 AL A unit of count defining the number of telephone access lines. acre 2 acre 4 046,856 m² ACR + active unit 3.9 E25 A unit of count defining the number of active units within a substance. + activity 3.2 ACT A unit of count defining the number of activities (activity: a unit of work or action). X actual ton 3.1 26 | additional minute 3.5 AH A unit of time defining the number of minutes in addition to the referenced minutes. | air dry metric ton 3.1 MD A unit of count defining the number of metric tons of a product, disregarding the water content of the product. -

Not Made to Measure
Made in Britain: Not made to measure. Ronnie Cohen © 2011 Ronnie Cohen. All rights reserved. 1 Table of Contents Foreword...............................................................................................................................................5 Introduction..........................................................................................................................................6 Central Role of Measurement in Daily Life.........................................................................................7 Why Measurement Matters..................................................................................................................8 Quest for Honest Measurements since Ancient Times.........................................................................9 Measurement Facts: Did you know that....?.......................................................................................10 Description of the British Imperial System........................................................................................11 Introduction to the British Imperial System..............................................................................11 Units of Length..........................................................................................................................11 Units of Area.............................................................................................................................11 Units of Volume........................................................................................................................12 -

Units of Measurement to Be Used in Air and Ground Operations
International Standards and Recommended Practices Annex 5 to the Convention on International Civil Aviation Units of Measurement to be Used in Air and Ground Operations This edition incorporates all amendments adopted by the Council prior to 23 February 2010 and supersedes, on 18 November 2010, all previous editions of Annex 5. For information regarding the applicability of the Standards and Recommended Practices,see Foreword. Fifth Edition July 2010 International Civil Aviation Organization Suzanne TRANSMITTAL NOTE NEW EDITIONS OF ANNEXES TO THE CONVENTION ON INTERNATIONAL CIVIL AVIATION It has come to our attention that when a new edition of an Annex is published, users have been discarding, along with the previous edition of the Annex, the Supplement to the previous edition. Please note that the Supplement to the previous edition should be retained until a new Supplement is issued. Suzanne International Standards and Recommended Practices Annex 5 to the Convention on International Civil Aviation Units of Measurement to be Used in Air and Ground Operations ________________________________ This edition incorporates all amendments adopted by the Council prior to 23 February 2010 and supersedes, on 18 November 2010, all previous editions of Annex 5. For information regarding the applicability of the Standards and Recommended Practices, see Foreword. Fifth Edition July 2010 International Civil Aviation Organization Published in separate English, Arabic, Chinese, French, Russian and Spanish editions by the INTERNATIONAL CIVIL AVIATION ORGANIZATION 999 University Street, Montréal, Quebec, Canada H3C 5H7 For ordering information and for a complete listing of sales agents and booksellers, please go to the ICAO website at www.icao.int First edition 1948 Fourth edition 1979 Fifth edition 2010 Annex 5, Units of Measurement to be Used in Air and Ground Operations Order Number: AN 5 ISBN 978-92-9231-512-2 © ICAO 2010 All rights reserved. -

Metrication Is SUCCESSFUL
Metrication is SUCCESSFUL Metrication is SUCCESSFUL because it is: Simple The modern metric system, formally known as the International System of Units (SI), is the simplest and easiest-to-use system of measurement ever devised. In fact the metric system is the only system of measurement ever devised. All previous measuring methods were just a hodge-podge of randomly generated local measures. Unique The metric system is unique. Never before, has there been a method of measurement that has all the positive benefits as SI. Coherent The metric system uses the same decimal nature as our number system, and it uses the same mathematical rules and symbols that we use for the mathematic of numbers Capable The metric system is capable of measuring anything in any trade, profession, or other human activity. The metric system has no limitations. For example, you might measure the distance from here to the door in metres, the distance from between your home and your work in kilometres, the width of your little finger nail in millimetres, the diameter of the hairs on your head in micrometres, and the size of one of your cells in nanometres. Why stop there? With the SI prefixes, there is more than enough flexibility to measure from the size of sub-atomic particles – the diameter of an electron is about 6 femtometres – to the size of the whole Universe – the diameter of the Universe, as observed by the world's best telescopes, is about 250 yottametres. Equitable The key argument for using the metric system is that it is fair to all concerned. -

Harnessing Speckle for a Sub-Femtometre Resolved Broadband Wavemeter and Laser Stabilization
ARTICLE Received 8 Oct 2016 | Accepted 12 Apr 2017 | Published 5 Jun 2017 DOI: 10.1038/ncomms15610 OPEN Harnessing speckle for a sub-femtometre resolved broadband wavemeter and laser stabilization Nikolaus Klaus Metzger1, Roman Spesyvtsev1, Graham D. Bruce1, Bill Miller2, Gareth T. Maker2, Graeme Malcolm2, Michael Mazilu1 & Kishan Dholakia1 The accurate determination and control of the wavelength of light is fundamental to many fields of science. Speckle patterns resulting from the interference of multiple reflections in disordered media are well-known to scramble the information content of light by complex but linear processes. However, these patterns are, in fact, exceptionally rich in information about the illuminating source. We use a fibre-coupled integrating sphere to generate wavelength- dependent speckle patterns, in combination with algorithms based on the transmission matrix method and principal component analysis, to realize a broadband and sensitive wavemeter. We demonstrate sub-femtometre wavelength resolution at a centre wavelength of 780 nm, and a broad calibrated measurement range from 488 to 1,064 nm. This compares favourably to the performance of conventional wavemeters. Using this speckle wavemeter as part of a feedback loop, we stabilize a 780 nm diode laser to achieve a linewidth better than 1 MHz. 1 SUPA, School of Physics and Astronomy, University of St Andrews, Scotland KY16 9SS, UK. 2 M Squared Lasers Ltd, Venture Building, 1 Kelvin Campus, West of Scotland Science Park, Glasgow G20 0SP, UK. Correspondence and requests for materials should be addressed to K.D. (email: [email protected]). NATURE COMMUNICATIONS | 8:15610 | DOI: 10.1038/ncomms15610 | www.nature.com/naturecommunications 1 ARTICLE NATURE COMMUNICATIONS | DOI: 10.1038/ncomms15610 ight propagation in disordered media is often regarded as a the picometre level and operating ranges of over 1 mm covering randomization process by which the information contained the visible and near-infrared spectrum. -

Stabilization of Nanometre-Size Particle Beams in the Final Focus System of the Compact Linear Collider (CLIC)
EUROPEAN ORGANIZATION FOR NUCLEAR RESEARCH CERN – AB DEPARTMENT CERN–AB–2004–026 (ABP) CLIC-Note 595 Stabilization of Nanometre-Size Particle Beams in the Final Focus System of the Compact LInear Collider (CLIC) Stefano Redaelli ∗ Abstract The Compact LInear Collider (CLIC) study at the European Organization for Nu- clear Research (CERN) is developing the design of a 3 TeV e+e− linear collider. The discovery reach of this machine depends on obtaining a luminosity of 1035 cm−2s−1, which will be done by colliding beams with transverse spot sizes in the nanometre range ( 60 0:7 nm2). Tolerances on fast mechanical stability of the focusing quadrupo- les≈ reach×the 0.2 nm level. The serious concern of magnet stabilization for future linear colliders has been addressed by building a CERN test stand on magnet stability, bring- ing together state-of-the-art stabilization technology, latest equipment for vibration mea- surements and realistic magnet prototypes. For the first time an accelerator magnet was successfully stabilized to the sub-nanometre level, reducing its vibrations level by one order of magnitude with respect to the supporting ground. The best measurements indi- cate transverse RMS vibration amplitudes (above 4 Hz) of (0.79 0.08) nm horizontally and (0.43 0.04) nm vertically, maintained to a maximum of less than (1.47 0.15) nm and (1.000.10) nm, respectively, over a period of several days. Detailed simulations of time-dependent luminosity, which use a model for magnet displacements based on mea- sured vibration spectra, show that approximately 70% of the CLIC goal luminosity can be achieved with the demonstrated performance in the CERN test stand. -

6411 Measure Unit Qualifier Indication of the Unit of Measurement in Which Weight (Mass), Capacity, Length, Area, Volume Or Other Quantity Is Expressed
Code list 6411 Standard: UN D.97B S3 6411 Measure unit qualifier Indication of the unit of measurement in which weight (mass), capacity, length, area, volume or other quantity is expressed. Note: See UN/ECE Recommendation 20. 04 small spray 05 lift 08 heat lot 10 group 11 outfit 13 ration 14 shot 15 stick 16 hundred fifteen kg drum 17 hundred lb drum 18 fiftyfive gallon (US) drum 19 tank truck 20 twenty foot container 21 forty foot container 22 decilitre per gram 23 gram per cubic centimetre 24 theoretical pound 25 gram per square centimetre 26 actual ton 27 theoretical ton 28 kilogram per square metre 29 pound per thousand square feet 30 horse power day per air dry metric ton 31 catch weight 32 kilogram per air dry metric ton 33 kilopascal square metres per gram 34 kilopascals per millimetre 35 millilitres per square centimetre second 36 cubic feet per minute per square foot 37 ounce per square foot 38 ounces per square foot per 0,01 inch 40 millilitre per second 41 millilitre per minute 43 super bulk bag 44 fivehundred kg bulk bag 45 threehundred kg bulk bag 46 fifty lb bulk bag 47 fifty lb bag 48 bulk car load 53 theoretical kilograms Printed by GEFEG EDIFIX® Print date: 25/09/2001 Page: 1 Code list 6411 Standard: UN D.97B S3 54 theoretical tonne 56 sitas 57 mesh 58 net kilogram 59 part per million 60 percent weight 61 part per billion (US) 62 percent per 1000 hour 63 failure rate in time 64 pound per square inch, gauge 66 oersted 69 test specific scale 71 volt ampere per pound 72 watt per pound 73 ampere tum per centimetre 74 millipascal -

Quantities, Units and Symbols in Physical Chemistry Third Edition
INTERNATIONAL UNION OF PURE AND APPLIED CHEMISTRY Physical and Biophysical Chemistry Division 1 7 2 ) + Quantities, Units and Symbols in Physical Chemistry Third Edition Prepared for publication by E. Richard Cohen Tomislav Cvitaš Jeremy G. Frey Bertil Holmström Kozo Kuchitsu Roberto Marquardt Ian Mills Franco Pavese Martin Quack Jürgen Stohner Herbert L. Strauss Michio Takami Anders J Thor The first and second editions were prepared for publication by Ian Mills Tomislav Cvitaš Klaus Homann Nikola Kallay Kozo Kuchitsu IUPAC 2007 Professor E. Richard Cohen Professor Tom Cvitaš 17735, Corinthian Drive University of Zagreb Encino, CA 91316-3704 Department of Chemistry USA Horvatovac 102a email: [email protected] HR-10000 Zagreb Croatia email: [email protected] Professor Jeremy G. Frey Professor Bertil Holmström University of Southampton Ulveliden 15 Department of Chemistry SE-41674 Göteborg Southampton, SO 17 1BJ Sweden United Kingdom email: [email protected] email: [email protected] Professor Kozo Kuchitsu Professor Roberto Marquardt Tokyo University of Agriculture and Technology Laboratoire de Chimie Quantique Graduate School of BASE Institut de Chimie Naka-cho, Koganei Université Louis Pasteur Tokyo 184-8588 4, Rue Blaise Pascal Japan F-67000 Strasbourg email: [email protected] France email: [email protected] Professor Ian Mills Professor Franco Pavese University of Reading Instituto Nazionale di Ricerca Metrologica (INRIM) Department of Chemistry strada delle Cacce 73-91 Reading, RG6 6AD I-10135 Torino United Kingdom Italia email: [email protected] email: [email protected] Professor Martin Quack Professor Jürgen Stohner ETH Zürich ZHAW Zürich University of Applied Sciences Physical Chemistry ICBC Institute of Chemistry & Biological Chemistry CH-8093 Zürich Campus Reidbach T, Einsiedlerstr.