DOCSLIB.ORG

Unit 3: Linear Algebra 1: Matrices and Least Squares

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Unit 3: Linear Algebra 1: Matrices and Least Squares DRAFT V1.2 From Math, Numerics, & Programming (for Mechanical Engineers) Masayuki Yano James Douglass Penn George Konidaris Anthony T Patera September 2012 © The Authors. License: Creative Commons Attribution-Noncommercial-Share Alike 3.0 (CC BY-NC-SA 3.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and MIT OpenCourseWare source are credited; the use is non-commercial; and the CC BY-NC-SA license is retained. See also http://ocw.mit.edu/terms/. Contents III Linear Algebra 1: Matrices and Least Squares. Regression. 199 15 Motivation 201 16 Matrices and Vectors: Definitions and Operations 203 16.1 Basic Vector and Matrix Operations ........................... 203 16.1.1 Definitions ..................................... 203 Transpose Operation ... ... ... ... ... ... ... ... ... 204 16.1.2 Vector Operations ................................. 205 Inner Product ... ... ... ... ... ... ... ... ... ... 207 Norm (2-Norm) .. ... ... ... ... ... ... ... ... ... 207 Orthogonality ... ... ... ... ... .. ... ... ... ... 211 Orthonormality .. ... ... ... ... ... ... ... ... ... 212 16.1.3 Linear Combinations ................................ 212 Linear Independence .. ... ... ... ... ... ... ... ... 213 Vector Spaces and Bases . ... ... ... ... ... ... ... ... 214 16.2 Matrix Operations ..................................... 217 16.2.1 Interpretation of Matrices ............................. 217 16.2.2 Matrix Operations ................................. 218 Matrix-Matrix Product .............................. 219 16.2.3 Interpretations of the Matrix-Vector Product . 222 Row Interpretation . ... ... ... ... ... ... ... ... ... 222 Column Interpretation .. ... ... ... ... ... ... ... ... 223 Left Vector-Matrix Product .. ... ... ... ... ... ... ... 223 16.2.4 Interpretations of the Matrix-Matrix Product . 224 Matrix-Matrix Product as a Series of Matrix-Vector Products . 224 Matrix-Matrix Product as a Series of Left Vector-Matrix Products . 225 16.2.5 Operation Count of Matrix-Matrix Product ................... 225 16.2.6 The Inverse of a Matrix (Briefly) ......................... 226 16.3 Special Matrices ...................................... 227 16.3.1 Diagonal Matrices ................................. 228 16.3.2 Symmetric Matrices ................................ 228 16.3.3 Symmetric Positive Definite Matrices ....................... 228 16.3.4 Triangular Matrices ................................ 230 16.3.5 Orthogonal Matrices ................................ 230 16.3.6 Orthonormal Matrices ............................... 232 16.4 Further Concepts in Linear Algebra ........................... 233 16.4.1 Column Space and Null Space .......................... 233 16.4.2 Projectors ...................................... 234 3 17 Least Squares 237 17.1 Data Fitting in Absence of Noise and Bias ....................... 237 17.2 Overdetermined Systems .. ... ... ... ... ... ... ... ... ... 242 Row Interpretation . ... ... ... ... ... ... ... ... ... 243 Column Interpretation .. ... ... ... ... ... ... ... ... 244 17.3 Least Squares . ... ... ... ... ... ... ... ... ... ... .. 245 17.3.1 Measures of Closeness ............................... 245 17.3.2 Least-Squares Formulation (`2 minimization) .................. 246 17.3.3 Computational Considerations .......................... 250 QR Factorization and the Gram-Schmidt Procedure . 251 17.3.4 Interpretation of Least Squares: Projection . 253 17.3.5 Error Bounds for Least Squares .......................... 255 Error Bounds with Respect to Perturbation in Data, g (constant model) . 255 Error Bounds with Respect to Perturbation in Data, g (general) ....... 256 Error Bounds with Respect to Reduction in Space, B . ... ... ... 262 18 Matlab Linear Algebra (Briefly) 267 18.1 Matrix Multiplication (and Addition) .......................... 267 18.2 The Matlab Inverse Function: inv . ... ... ... ... ... ... ... 268 18.3 Solution of Linear Systems: Matlab Backslash .. ... ... ... ... ... 269 18.4 Solution of (Linear) Least-Squares Problems . ... ... ... ... ... ... 269 19 Regression: Statistical Inference 271 19.1 Simplest Case . ... ... ... ... ... ... ... .. ... ... ... 271 19.1.1 Friction Coefficient Determination Problem Revisited . 271 19.1.2 Response Model .................................. 272 19.1.3 Parameter Estimation ............................... 275 19.1.4 Confidence Intervals ................................ 277 Individual Confidence Intervals .......................... 278 Joint Confidence Intervals ... ... ... ... ... ... ... ... 279 19.1.5 Hypothesis Testing ................................. 284 19.1.6 Inspection of Assumptions ............................. 285 Checking for Plausibility of the Noise Assumptions . 285 Checking for Presence of Bias .. ... ... .. ... ... ... ... 286 19.2 General Case ........................................ 287 19.2.1 Response Model .................................. 287 19.2.2 Estimation ..................................... 288 19.2.3 Confidence Intervals ................................ 289 19.2.4 Overfitting (and Underfitting) .......................... 290 4 Unit III Linear Algebra 1: Matrices and Least Squares. Regression. 199 Chapter 15 Motivation DRAFT V1.2 © The Authors. License: Creative Commons BY-NC-SA 3.0 . In odometry-based mobile robot navigation, the accuracy of the robot’s dead reckoning pose tracking depends on minimizing slippage between the robot’s wheels and the ground. Even a momentary slip can lead to an error in heading that will cause the error in the robot’s location estimate to grow linearly over its journey. It is thus important to determine the friction coefficient between the robot’s wheels and the ground, which directly affects the robot’s resistance to slippage. Just as importantly, this friction coefficient will significantly affect the performance of the robot: the ability to push loads. When the mobile robot of Figure 15.1 is commanded to move forward, a number of forces come into play. Internally, the drive motors exert a torque (not shown in the figure) on the wheels, which is resisted by the friction force Ff between the wheels and the ground. If the magnitude of Ff dictated by the sum of the drag force Fdrag (a combination of all forces resisting the robot’s motion) and the product of the robot’s mass and acceleration is less than the maximum static friction force max Ff ; static between the wheels and the ground, the wheels will roll without slipping and the robot max will move forward with velocity v = !rwheel. If, however, the magnitude of Ff reaches Ff ; static, the wheels will begin to slip and Ff will drop to a lower level Ff; kinetic, the kinetic friction force. The wheels will continue to slip (v < !rwheel) until zero relative motion between the wheels and the ground is restored (when v = !rwheel). The critical value defining the boundary between rolling and slipping, therefore, is the maximum w v Fdrag W Ff Fnormal, front Fnormal, rear Figure 15.1: A mobile robot in motion. 201 Ffriction vs. Time for 500 Gram Load max, meas 0.9 Ff, static = µs Fnor mal + experimental error 0.8 0.7 0.6 meas F = µk Fnormal + experimental error (Newtons) 0.5 f, kinetic 0.4 friction 0.3 F 0.2 Ff, static = Ftangential, applied µs Fnormal 0.1 ≤ 0 1 2 3 4 5 6 7 8 time (seconds) Figure 15.2: Experimental setup for friction measurement: Force transducer (A) is con- Figure 15.3: Sample data for one friction nected to contact area (B) by a thin wire. measurement, yielding one data point for max; meas Normal force is exerted on the contact area Ff ; static . Data courtesy of James Penn. by load stack (C). Tangential force is ap­ plied using turntable (D) via the friction be­ tween the turntable surface and the contact area. Apparatus and photograph courtesy of James Penn. static friction force. We expect that max Ff ; static = µs Fnormal; rear ; (15.1) where µs is the static coefficient of friction and Fnormal; rear is the normal force from the ground on the rear, driving, wheels. In order to minimize the risk of slippage (and to be able to push large loads), robot wheels should be designed for a high value of µs between the wheels and the ground. This value, although difficult to predict accurately by modeling, can be determined by experiment. max We first conduct experiments for the friction force Ff ; static (in Newtons) as a function of normal 2 load Fnormal; applied (in Newtons) and (nominal) surface area of contact Asurface (in cm ) with the friction turntable apparatus depicted in Figure 15.2. Weights permit us to vary the normal load and “washer” inserts permit us to vary the nominal surface area of contact. A typical experiment (at a particular prescribed value of Fnormal; applied and Asurface) yields the time trace of Figure 15.3 from max; means max which the Ff ; static (our measurement of F f; static) is deduced as the maximum of the response. We next postulate a dependence (or “model”) max Ff ; static(Fnormal; applied;Asurface) = β0 + β1 Fnormal; applied + β2 Asurface ; (15.2) where we expect — but do not a priori assume — from Messieurs Amontons and Coulomb that β0 = 0 and β2 = 0 (and of course β1 ≡ µs). In order to confirm that β0 = 0 and β2 = 0 — or at least confirm that β0 = 0 and β2 = 0 is not untrue — and to find a good estimate for β1 ≡ µs, we must appeal to our measurements. The mathematical techniques by which to determine µs (and β0, β2) “with some confidence” from noisy experimental data is known as regression, which is the subject of Chapter 19. Regression, in turn, is best described
Load more

Recommended publications
  • 8.5 Least Squares Solutions to Inconsistent Systems
    8.5 Least Squares Solutions to Inconsistent Systems Performance Criterion: 8. (f) Find the least-squares approximation to the solution of an inconsistent system of equations. Solve a problem using least-squares approximation. (g) Give the least squares error and least squares error vector for a least squares approximation to a solution to a system of equations. Recall that an inconsistent system is one for which there is no solution. Often we wish to solve inconsistent systems and it is just not acceptable to have no solution. In those cases we can find some vector (whose components are the values we are trying to find when attempting to solve the system) that is “closer to being a solution” than all other vectors. The theory behind this process is part of the second term of this course, but we now have enough knowledge to find such a vector in a “cookbook” manner. Suppose that we have a system of equations Ax = b. Pause for a moment to reflect on what we know and what we are trying to find when solving such a system: We have a system of linear equations, and the entries of A are the coefficients of all the equations. The vector b is the vector whose components are the right sides of all the equations, and the vector x is the vector whose components are the unknown values of the variables we are trying to find. So we know A and b and we are trying to find x. If A is invertible, the solution vector x is given by x = A−1 b.
    [Show full text]
  • 1111: Linear Algebra I
    1111: Linear Algebra I Dr. Vladimir Dotsenko (Vlad) Lecture 11 Dr. Vladimir Dotsenko (Vlad) 1111: Linear Algebra I Lecture 11 1 / 13 Previously on. Theorem. Let A be an n × n-matrix, and b a vector with n entries. The following statements are equivalent: (a) the homogeneous system Ax = 0 has only the trivial solution x = 0; (b) the reduced row echelon form of A is In; (c) det(A) 6= 0; (d) the matrix A is invertible; (e) the system Ax = b has exactly one solution. A very important consequence (finite dimensional Fredholm alternative): For an n × n-matrix A, the system Ax = b either has exactly one solution for every b, or has infinitely many solutions for some choices of b and no solutions for some other choices. In particular, to prove that Ax = b has solutions for every b, it is enough to prove that Ax = 0 has only the trivial solution. Dr. Vladimir Dotsenko (Vlad) 1111: Linear Algebra I Lecture 11 2 / 13 An example for the Fredholm alternative Let us consider the following question: Given some numbers in the first row, the last row, the first column, and the last column of an n × n-matrix, is it possible to fill the numbers in all the remaining slots in a way that each of them is the average of its 4 neighbours? This is the \discrete Dirichlet problem", a finite grid approximation to many foundational questions of mathematical physics. Dr. Vladimir Dotsenko (Vlad) 1111: Linear Algebra I Lecture 11 3 / 13 An example for the Fredholm alternative For instance, for n = 4 we may face the following problem: find a; b; c; d to put in the matrix 0 4 3 0 1:51 B 1 a b -1C B C @0:5 c d 2 A 2:1 4 2 1 so that 1 a = 4 (3 + 1 + b + c); 1 8b = 4 (a + 0 - 1 + d); >c = 1 (a + 0:5 + d + 4); > 4 < 1 d = 4 (b + c + 2 + 2): > > This is a system with 4:> equations and 4 unknowns.
    [Show full text]
  • 21. Orthonormal Bases
    21. Orthonormal Bases The canonical/standard basis 011 001 001 B C B C B C B0C B1C B0C e1 = B.C ; e2 = B.C ; : : : ; en = B.C B.C B.C B.C @.A @.A @.A 0 0 1 has many useful properties. • Each of the standard basis vectors has unit length: q p T jjeijj = ei ei = ei ei = 1: • The standard basis vectors are orthogonal (in other words, at right angles or perpendicular). T ei ej = ei ej = 0 when i 6= j This is summarized by ( 1 i = j eT e = δ = ; i j ij 0 i 6= j where δij is the Kronecker delta. Notice that the Kronecker delta gives the entries of the identity matrix. Given column vectors v and w, we have seen that the dot product v w is the same as the matrix multiplication vT w. This is the inner product on n T R . We can also form the outer product vw , which gives a square matrix. 1 The outer product on the standard basis vectors is interesting. Set T Π1 = e1e1 011 B C B0C = B.C 1 0 ::: 0 B.C @.A 0 01 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 0 . T Πn = enen 001 B C B0C = B.C 0 0 ::: 1 B.C @.A 1 00 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 1 In short, Πi is the diagonal square matrix with a 1 in the ith diagonal position and zeros everywhere else.
    [Show full text]
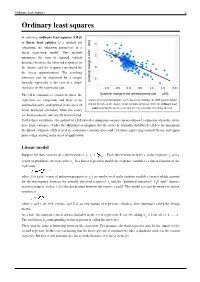
  • Ordinary Least Squares 1 Ordinary Least Squares
    Ordinary least squares 1 Ordinary least squares In statistics, ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear approximation. The resulting estimator can be expressed by a simple formula, especially in the case of a single regressor on the right-hand side. The OLS estimator is consistent when the regressors are exogenous and there is no Okun's law in macroeconomics states that in an economy the GDP growth should multicollinearity, and optimal in the class of depend linearly on the changes in the unemployment rate. Here the ordinary least squares method is used to construct the regression line describing this law. linear unbiased estimators when the errors are homoscedastic and serially uncorrelated. Under these conditions, the method of OLS provides minimum-variance mean-unbiased estimation when the errors have finite variances. Under the additional assumption that the errors be normally distributed, OLS is the maximum likelihood estimator. OLS is used in economics (econometrics) and electrical engineering (control theory and signal processing), among many areas of application. Linear model Suppose the data consists of n observations { y , x } . Each observation includes a scalar response y and a i i i vector of predictors (or regressors) x . In a linear regression model the response variable is a linear function of the i regressors: where β is a p×1 vector of unknown parameters; ε 's are unobserved scalar random variables (errors) which account i for the discrepancy between the actually observed responses y and the "predicted outcomes" x′ β; and ′ denotes i i matrix transpose, so that x′ β is the dot product between the vectors x and β.
    [Show full text]
  • 1 Euclidean Vector Space and Euclidean Affi Ne Space
    Profesora: Eugenia Rosado. E.T.S. Arquitectura. Euclidean Geometry1 1 Euclidean vector space and euclidean a¢ ne space 1.1 Scalar product. Euclidean vector space. Let V be a real vector space. De…nition. A scalar product is a map (denoted by a dot ) V V R ! (~u;~v) ~u ~v 7! satisfying the following axioms: 1. commutativity ~u ~v = ~v ~u 2. distributive ~u (~v + ~w) = ~u ~v + ~u ~w 3. ( ~u) ~v = (~u ~v) 4. ~u ~u 0, for every ~u V 2 5. ~u ~u = 0 if and only if ~u = 0 De…nition. Let V be a real vector space and let be a scalar product. The pair (V; ) is said to be an euclidean vector space. Example. The map de…ned as follows V V R ! (~u;~v) ~u ~v = x1x2 + y1y2 + z1z2 7! where ~u = (x1; y1; z1), ~v = (x2; y2; z2) is a scalar product as it satis…es the …ve properties of a scalar product. This scalar product is called standard (or canonical) scalar product. The pair (V; ) where is the standard scalar product is called the standard euclidean space. 1.1.1 Norm associated to a scalar product. Let (V; ) be a real euclidean vector space. De…nition. A norm associated to the scalar product is a map de…ned as follows V kk R ! ~u ~u = p~u ~u: 7! k k Profesora: Eugenia Rosado, E.T.S. Arquitectura. Euclidean Geometry.2 1.1.2 Unitary and orthogonal vectors. Orthonormal basis. Let (V; ) be a real euclidean vector space. De…nition.
    [Show full text]
  • Lecture 4: April 8, 2021 1 Orthogonality and Orthonormality
    Mathematical Toolkit Spring 2021 Lecture 4: April 8, 2021 Lecturer: Avrim Blum (notes based on notes from Madhur Tulsiani) 1 Orthogonality and orthonormality Definition 1.1 Two vectors u, v in an inner product space are said to be orthogonal if hu, vi = 0. A set of vectors S ⊆ V is said to consist of mutually orthogonal vectors if hu, vi = 0 for all u 6= v, u, v 2 S. A set of S ⊆ V is said to be orthonormal if hu, vi = 0 for all u 6= v, u, v 2 S and kuk = 1 for all u 2 S. Proposition 1.2 A set S ⊆ V n f0V g consisting of mutually orthogonal vectors is linearly inde- pendent. Proposition 1.3 (Gram-Schmidt orthogonalization) Given a finite set fv1,..., vng of linearly independent vectors, there exists a set of orthonormal vectors fw1,..., wng such that Span (fw1,..., wng) = Span (fv1,..., vng) . Proof: By induction. The case with one vector is trivial. Given the statement for k vectors and orthonormal fw1,..., wkg such that Span (fw1,..., wkg) = Span (fv1,..., vkg) , define k u + u = v − hw , v i · w and w = k 1 . k+1 k+1 ∑ i k+1 i k+1 k k i=1 uk+1 We can now check that the set fw1,..., wk+1g satisfies the required conditions. Unit length is clear, so let’s check orthogonality: k uk+1, wj = vk+1, wj − ∑ hwi, vk+1i · wi, wj = vk+1, wj − wj, vk+1 = 0. i=1 Corollary 1.4 Every finite dimensional inner product space has an orthonormal basis.
    [Show full text]
  • Orthonormality and the Gram-Schmidt Process
    Unit 4, Section 2: The Gram-Schmidt Process Orthonormality and the Gram-Schmidt Process The basis (e1; e2; : : : ; en) n n for R (or C ) is considered the standard basis for the space because of its geometric properties under the standard inner product: 1. jjeijj = 1 for all i, and 2. ei, ej are orthogonal whenever i 6= j. With this idea in mind, we record the following definitions: Definitions 6.23/6.25. Let V be an inner product space. • A list of vectors in V is called orthonormal if each vector in the list has norm 1, and if each pair of distinct vectors is orthogonal. • A basis for V is called an orthonormal basis if the basis is an orthonormal list. Remark. If a list (v1; : : : ; vn) is orthonormal, then ( 0 if i 6= j hvi; vji = 1 if i = j: Example. The list (e1; e2; : : : ; en) n n forms an orthonormal basis for R =C under the standard inner products on those spaces. 2 Example. The standard basis for Mn(C) consists of n matrices eij, 1 ≤ i; j ≤ n, where eij is the n × n matrix with a 1 in the ij entry and 0s elsewhere. Under the standard inner product on Mn(C) this is an orthonormal basis for Mn(C): 1. heij; eiji: ∗ heij; eiji = tr (eijeij) = tr (ejieij) = tr (ejj) = 1: 1 Unit 4, Section 2: The Gram-Schmidt Process 2. heij; ekli, k 6= i or j 6= l: ∗ heij; ekli = tr (ekleij) = tr (elkeij) = tr (0) if k 6= i, or tr (elj) if k = i but l 6= j = 0: So every vector in the list has norm 1, and every distinct pair of vectors is orthogonal.
    [Show full text]
  • Glossary of Linear Algebra Terms
    INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w.
    [Show full text]
  • Vector Differential Calculus
    KAMIWAAI – INTERACTIVE 3D SKETCHING WITH JAVA BASED ON Cl(4,1) CONFORMAL MODEL OF EUCLIDEAN SPACE Submitted to (Feb. 28,2003): Advances in Applied Clifford Algebras, http://redquimica.pquim.unam.mx/clifford_algebras/ Eckhard M. S. Hitzer Dept. of Mech. Engineering, Fukui Univ. Bunkyo 3-9-, 910-8507 Fukui, Japan. Email: [email protected], homepage: http://sinai.mech.fukui-u.ac.jp/ Abstract. This paper introduces the new interactive Java sketching software KamiWaAi, recently developed at the University of Fukui. Its graphical user interface enables the user without any knowledge of both mathematics or computer science, to do full three dimensional “drawings” on the screen. The resulting constructions can be reshaped interactively by dragging its points over the screen. The programming approach is new. KamiWaAi implements geometric objects like points, lines, circles, spheres, etc. directly as software objects (Java classes) of the same name. These software objects are geometric entities mathematically defined and manipulated in a conformal geometric algebra, combining the five dimensions of origin, three space and infinity. Simple geometric products in this algebra represent geometric unions, intersections, arbitrary rotations and translations, projections, distance, etc. To ease the coordinate free and matrix free implementation of this fundamental geometric product, a new algebraic three level approach is presented. Finally details about the Java classes of the new GeometricAlgebra software package and their associated methods are given. KamiWaAi is available for free internet download. Key Words: Geometric Algebra, Conformal Geometric Algebra, Geometric Calculus Software, GeometricAlgebra Java Package, Interactive 3D Software, Geometric Objects 1. Introduction The name “KamiWaAi” of this new software is the Romanized form of the expression in verse sixteen of chapter four, as found in the Japanese translation of the first Letter of the Apostle John, which is part of the New Testament, i.e.
    [Show full text]
  • Linear Algebra I
    Linear Algebra I Gregg Waterman Oregon Institute of Technology c 2016 Gregg Waterman This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The essence of the license is that You are free: to Share to copy, distribute and transmit the work • to Remix to adapt the work • Under the following conditions: Attribution You must attribute the work in the manner specified by the author (but not in • any way that suggests that they endorse you or your use of the work). Please contact the author at [email protected] to determine how best to make any attribution. Noncommercial You may not use this work for commercial purposes. • Share Alike If you alter, transform, or build upon this work, you may distribute the resulting • work only under the same or similar license to this one. With the understanding that: Waiver Any of the above conditions can be waived if you get permission from the copyright • holder. Public Domain Where the work or any of its elements is in the public domain under applicable • law, that status is in no way affected by the license. Other Rights In no way are any of the following rights affected by the license: • Your fair dealing or fair use rights, or other applicable copyright exceptions and limitations; ⋄ The author’s moral rights; ⋄ Rights other persons may have either in the work itself or in how the work is used, such as ⋄ publicity or privacy rights. Notice For any reuse or distribution, you must make clear to others the license terms of this • work.
    [Show full text]
  • Basics of Linear Algebra
    Basics of Linear Algebra Jos and Sophia Vectors ● Linear Algebra Definition: A list of numbers with a magnitude and a direction. ○ Magnitude: a = [4,3] |a| =sqrt(4^2+3^2)= 5 ○ Direction: angle vector points ● Computer Science Definition: A list of numbers. ○ Example: Heights = [60, 68, 72, 67] Dot Product of Vectors Formula: a · b = |a| × |b| × cos(θ) ● Definition: Multiplication of two vectors which results in a scalar value ● In the diagram: ○ |a| is the magnitude (length) of vector a ○ |b| is the magnitude of vector b ○ Θ is the angle between a and b Matrix ● Definition: ● Matrix elements: ● a)Matrix is an arrangement of numbers into rows and columns. ● b) A matrix is an m × n array of scalars from a given field F. The individual values in the matrix are called entries. ● Matrix dimensions: the number of rows and columns of the matrix, in that order. Multiplication of Matrices ● The multiplication of two matrices ● Result matrix dimensions ○ Notation: (Row, Column) ○ Columns of the 1st matrix must equal the rows of the 2nd matrix ○ Result matrix is equal to the number of (1, 2, 3) • (7, 9, 11) = 1×7 +2×9 + 3×11 rows in 1st matrix and the number of = 58 columns in the 2nd matrix ○ Ex. 3 x 4 ॱ 5 x 3 ■ Dot product does not work ○ Ex. 5 x 3 ॱ 3 x 4 ■ Dot product does work ■ Result: 5 x 4 Dot Product Application ● Application: Ray tracing program ○ Quickly create an image with lower quality ○ “Refinement rendering pass” occurs ■ Removes the jagged edges ○ Dot product used to calculate ■ Intersection between a ray and a sphere ■ Measure the length to the intersection points ● Application: Forward Propagation ○ Input matrix * weighted matrix = prediction matrix http://immersivemath.com/ila/ch03_dotprodu ct/ch03.html#fig_dp_ray_tracer Projections One important use of dot products is in projections.
    [Show full text]
  • Inner Product Spaces
    CHAPTER 6 Woman teaching geometry, from a fourteenth-century edition of Euclid’s geometry book. Inner Product Spaces In making the definition of a vector space, we generalized the linear structure (addition and scalar multiplication) of R2 and R3. We ignored other important features, such as the notions of length and angle. These ideas are embedded in the concept we now investigate, inner products. Our standing assumptions are as follows: 6.1 Notation F, V F denotes R or C. V denotes a vector space over F. LEARNING OBJECTIVES FOR THIS CHAPTER Cauchy–Schwarz Inequality Gram–Schmidt Procedure linear functionals on inner product spaces calculating minimum distance to a subspace Linear Algebra Done Right, third edition, by Sheldon Axler 164 CHAPTER 6 Inner Product Spaces 6.A Inner Products and Norms Inner Products To motivate the concept of inner prod- 2 3 x1 , x 2 uct, think of vectors in R and R as x arrows with initial point at the origin. x R2 R3 H L The length of a vector in or is called the norm of x, denoted x . 2 k k Thus for x .x1; x2/ R , we have The length of this vector x is p D2 2 2 x x1 x2 . p 2 2 x1 x2 . k k D C 3 C Similarly, if x .x1; x2; x3/ R , p 2D 2 2 2 then x x1 x2 x3 . k k D C C Even though we cannot draw pictures in higher dimensions, the gener- n n alization to R is obvious: we define the norm of x .x1; : : : ; xn/ R D 2 by p 2 2 x x1 xn : k k D C C The norm is not linear on Rn.
    [Show full text]