Glossary of Linear Algebra Terms
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

21. Orthonormal Bases
21. Orthonormal Bases The canonical/standard basis 011 001 001 B C B C B C B0C B1C B0C e1 = B.C ; e2 = B.C ; : : : ; en = B.C B.C B.C B.C @.A @.A @.A 0 0 1 has many useful properties. • Each of the standard basis vectors has unit length: q p T jjeijj = ei ei = ei ei = 1: • The standard basis vectors are orthogonal (in other words, at right angles or perpendicular). T ei ej = ei ej = 0 when i 6= j This is summarized by ( 1 i = j eT e = δ = ; i j ij 0 i 6= j where δij is the Kronecker delta. Notice that the Kronecker delta gives the entries of the identity matrix. Given column vectors v and w, we have seen that the dot product v w is the same as the matrix multiplication vT w. This is the inner product on n T R . We can also form the outer product vw , which gives a square matrix. 1 The outer product on the standard basis vectors is interesting. Set T Π1 = e1e1 011 B C B0C = B.C 1 0 ::: 0 B.C @.A 0 01 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 0 . T Πn = enen 001 B C B0C = B.C 0 0 ::: 1 B.C @.A 1 00 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 1 In short, Πi is the diagonal square matrix with a 1 in the ith diagonal position and zeros everywhere else. -

Multivector Differentiation and Linear Algebra 0.5Cm 17Th Santaló
Multivector differentiation and Linear Algebra 17th Santalo´ Summer School 2016, Santander Joan Lasenby Signal Processing Group, Engineering Department, Cambridge, UK and Trinity College Cambridge [email protected], www-sigproc.eng.cam.ac.uk/ s jl 23 August 2016 1 / 78 Examples of differentiation wrt multivectors. Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. Functional Differentiation: very briefly... Summary Overview The Multivector Derivative. 2 / 78 Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. Functional Differentiation: very briefly... Summary Overview The Multivector Derivative. Examples of differentiation wrt multivectors. 3 / 78 Functional Differentiation: very briefly... Summary Overview The Multivector Derivative. Examples of differentiation wrt multivectors. Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. 4 / 78 Summary Overview The Multivector Derivative. Examples of differentiation wrt multivectors. Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. Functional Differentiation: very briefly... 5 / 78 Overview The Multivector Derivative. Examples of differentiation wrt multivectors. Linear Algebra: matrices and tensors as linear functions mapping between elements of the algebra. Functional Differentiation: very briefly... Summary 6 / 78 We now want to generalise this idea to enable us to find the derivative of F(X), in the A ‘direction’ – where X is a general mixed grade multivector (so F(X) is a general multivector valued function of X). Let us use ∗ to denote taking the scalar part, ie P ∗ Q ≡ hPQi. Then, provided A has same grades as X, it makes sense to define: F(X + tA) − F(X) A ∗ ¶XF(X) = lim t!0 t The Multivector Derivative Recall our definition of the directional derivative in the a direction F(x + ea) − F(x) a·r F(x) = lim e!0 e 7 / 78 Let us use ∗ to denote taking the scalar part, ie P ∗ Q ≡ hPQi. -

1 Euclidean Vector Space and Euclidean Affi Ne Space
Profesora: Eugenia Rosado. E.T.S. Arquitectura. Euclidean Geometry1 1 Euclidean vector space and euclidean a¢ ne space 1.1 Scalar product. Euclidean vector space. Let V be a real vector space. De…nition. A scalar product is a map (denoted by a dot ) V V R ! (~u;~v) ~u ~v 7! satisfying the following axioms: 1. commutativity ~u ~v = ~v ~u 2. distributive ~u (~v + ~w) = ~u ~v + ~u ~w 3. ( ~u) ~v = (~u ~v) 4. ~u ~u 0, for every ~u V 2 5. ~u ~u = 0 if and only if ~u = 0 De…nition. Let V be a real vector space and let be a scalar product. The pair (V; ) is said to be an euclidean vector space. Example. The map de…ned as follows V V R ! (~u;~v) ~u ~v = x1x2 + y1y2 + z1z2 7! where ~u = (x1; y1; z1), ~v = (x2; y2; z2) is a scalar product as it satis…es the …ve properties of a scalar product. This scalar product is called standard (or canonical) scalar product. The pair (V; ) where is the standard scalar product is called the standard euclidean space. 1.1.1 Norm associated to a scalar product. Let (V; ) be a real euclidean vector space. De…nition. A norm associated to the scalar product is a map de…ned as follows V kk R ! ~u ~u = p~u ~u: 7! k k Profesora: Eugenia Rosado, E.T.S. Arquitectura. Euclidean Geometry.2 1.1.2 Unitary and orthogonal vectors. Orthonormal basis. Let (V; ) be a real euclidean vector space. De…nition. -
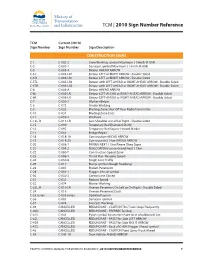
2010 Sign Number Reference for Traffic Control Manual
TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34 -

Math 217: Multilinearity of Determinants Professor Karen Smith (C)2015 UM Math Dept Licensed Under a Creative Commons By-NC-SA 4.0 International License
Math 217: Multilinearity of Determinants Professor Karen Smith (c)2015 UM Math Dept licensed under a Creative Commons By-NC-SA 4.0 International License. A. Let V −!T V be a linear transformation where V has dimension n. 1. What is meant by the determinant of T ? Why is this well-defined? Solution note: The determinant of T is the determinant of the B-matrix of T , for any basis B of V . Since all B-matrices of T are similar, and similar matrices have the same determinant, this is well-defined—it doesn't depend on which basis we pick. 2. Define the rank of T . Solution note: The rank of T is the dimension of the image. 3. Explain why T is an isomorphism if and only if det T is not zero. Solution note: T is an isomorphism if and only if [T ]B is invertible (for any choice of basis B), which happens if and only if det T 6= 0. 3 4. Now let V = R and let T be rotation around the axis L (a line through the origin) by an 21 0 0 3 3 angle θ. Find a basis for R in which the matrix of ρ is 40 cosθ −sinθ5 : Use this to 0 sinθ cosθ compute the determinant of T . Is T othogonal? Solution note: Let v be any vector spanning L and let u1; u2 be an orthonormal basis ? for V = L . Rotation fixes ~v, which means the B-matrix in the basis (v; u1; u2) has 213 first column 405. -

Determinants Math 122 Calculus III D Joyce, Fall 2012
Determinants Math 122 Calculus III D Joyce, Fall 2012 What they are. A determinant is a value associated to a square array of numbers, that square array being called a square matrix. For example, here are determinants of a general 2 × 2 matrix and a general 3 × 3 matrix. a b = ad − bc: c d a b c d e f = aei + bfg + cdh − ceg − afh − bdi: g h i The determinant of a matrix A is usually denoted jAj or det (A). You can think of the rows of the determinant as being vectors. For the 3×3 matrix above, the vectors are u = (a; b; c), v = (d; e; f), and w = (g; h; i). Then the determinant is a value associated to n vectors in Rn. There's a general definition for n×n determinants. It's a particular signed sum of products of n entries in the matrix where each product is of one entry in each row and column. The two ways you can choose one entry in each row and column of the 2 × 2 matrix give you the two products ad and bc. There are six ways of chosing one entry in each row and column in a 3 × 3 matrix, and generally, there are n! ways in an n × n matrix. Thus, the determinant of a 4 × 4 matrix is the signed sum of 24, which is 4!, terms. In this general definition, half the terms are taken positively and half negatively. In class, we briefly saw how the signs are determined by permutations. -

Matrices and Tensors
APPENDIX MATRICES AND TENSORS A.1. INTRODUCTION AND RATIONALE The purpose of this appendix is to present the notation and most of the mathematical tech- niques that are used in the body of the text. The audience is assumed to have been through sev- eral years of college-level mathematics, which included the differential and integral calculus, differential equations, functions of several variables, partial derivatives, and an introduction to linear algebra. Matrices are reviewed briefly, and determinants, vectors, and tensors of order two are described. The application of this linear algebra to material that appears in under- graduate engineering courses on mechanics is illustrated by discussions of concepts like the area and mass moments of inertia, Mohr’s circles, and the vector cross and triple scalar prod- ucts. The notation, as far as possible, will be a matrix notation that is easily entered into exist- ing symbolic computational programs like Maple, Mathematica, Matlab, and Mathcad. The desire to represent the components of three-dimensional fourth-order tensors that appear in anisotropic elasticity as the components of six-dimensional second-order tensors and thus rep- resent these components in matrices of tensor components in six dimensions leads to the non- traditional part of this appendix. This is also one of the nontraditional aspects in the text of the book, but a minor one. This is described in §A.11, along with the rationale for this approach. A.2. DEFINITION OF SQUARE, COLUMN, AND ROW MATRICES An r-by-c matrix, M, is a rectangular array of numbers consisting of r rows and c columns: ¯MM.. -

Vector Differential Calculus
KAMIWAAI – INTERACTIVE 3D SKETCHING WITH JAVA BASED ON Cl(4,1) CONFORMAL MODEL OF EUCLIDEAN SPACE Submitted to (Feb. 28,2003): Advances in Applied Clifford Algebras, http://redquimica.pquim.unam.mx/clifford_algebras/ Eckhard M. S. Hitzer Dept. of Mech. Engineering, Fukui Univ. Bunkyo 3-9-, 910-8507 Fukui, Japan. Email: [email protected], homepage: http://sinai.mech.fukui-u.ac.jp/ Abstract. This paper introduces the new interactive Java sketching software KamiWaAi, recently developed at the University of Fukui. Its graphical user interface enables the user without any knowledge of both mathematics or computer science, to do full three dimensional “drawings” on the screen. The resulting constructions can be reshaped interactively by dragging its points over the screen. The programming approach is new. KamiWaAi implements geometric objects like points, lines, circles, spheres, etc. directly as software objects (Java classes) of the same name. These software objects are geometric entities mathematically defined and manipulated in a conformal geometric algebra, combining the five dimensions of origin, three space and infinity. Simple geometric products in this algebra represent geometric unions, intersections, arbitrary rotations and translations, projections, distance, etc. To ease the coordinate free and matrix free implementation of this fundamental geometric product, a new algebraic three level approach is presented. Finally details about the Java classes of the new GeometricAlgebra software package and their associated methods are given. KamiWaAi is available for free internet download. Key Words: Geometric Algebra, Conformal Geometric Algebra, Geometric Calculus Software, GeometricAlgebra Java Package, Interactive 3D Software, Geometric Objects 1. Introduction The name “KamiWaAi” of this new software is the Romanized form of the expression in verse sixteen of chapter four, as found in the Japanese translation of the first Letter of the Apostle John, which is part of the New Testament, i.e. -

A Some Basic Rules of Tensor Calculus
A Some Basic Rules of Tensor Calculus The tensor calculus is a powerful tool for the description of the fundamentals in con- tinuum mechanics and the derivation of the governing equations for applied prob- lems. In general, there are two possibilities for the representation of the tensors and the tensorial equations: – the direct (symbolic) notation and – the index (component) notation The direct notation operates with scalars, vectors and tensors as physical objects defined in the three dimensional space. A vector (first rank tensor) a is considered as a directed line segment rather than a triple of numbers (coordinates). A second rank tensor A is any finite sum of ordered vector pairs A = a b + ... +c d. The scalars, vectors and tensors are handled as invariant (independent⊗ from the choice⊗ of the coordinate system) objects. This is the reason for the use of the direct notation in the modern literature of mechanics and rheology, e.g. [29, 32, 49, 123, 131, 199, 246, 313, 334] among others. The index notation deals with components or coordinates of vectors and tensors. For a selected basis, e.g. gi, i = 1, 2, 3 one can write a = aig , A = aibj + ... + cidj g g i i ⊗ j Here the Einstein’s summation convention is used: in one expression the twice re- peated indices are summed up from 1 to 3, e.g. 3 3 k k ik ik a gk ∑ a gk, A bk ∑ A bk ≡ k=1 ≡ k=1 In the above examples k is a so-called dummy index. Within the index notation the basic operations with tensors are defined with respect to their coordinates, e. -

New Foundations for Geometric Algebra1
Text published in the electronic journal Clifford Analysis, Clifford Algebras and their Applications vol. 2, No. 3 (2013) pp. 193-211 New foundations for geometric algebra1 Ramon González Calvet Institut Pere Calders, Campus Universitat Autònoma de Barcelona, 08193 Cerdanyola del Vallès, Spain E-mail : [email protected] Abstract. New foundations for geometric algebra are proposed based upon the existing isomorphisms between geometric and matrix algebras. Each geometric algebra always has a faithful real matrix representation with a periodicity of 8. On the other hand, each matrix algebra is always embedded in a geometric algebra of a convenient dimension. The geometric product is also isomorphic to the matrix product, and many vector transformations such as rotations, axial symmetries and Lorentz transformations can be written in a form isomorphic to a similarity transformation of matrices. We collect the idea Dirac applied to develop the relativistic electron equation when he took a basis of matrices for the geometric algebra instead of a basis of geometric vectors. Of course, this way of understanding the geometric algebra requires new definitions: the geometric vector space is defined as the algebraic subspace that generates the rest of the matrix algebra by addition and multiplication; isometries are simply defined as the similarity transformations of matrices as shown above, and finally the norm of any element of the geometric algebra is defined as the nth root of the determinant of its representative matrix of order n. The main idea of this proposal is an arithmetic point of view consisting of reversing the roles of matrix and geometric algebras in the sense that geometric algebra is a way of accessing, working and understanding the most fundamental conception of matrix algebra as the algebra of transformations of multiple quantities. -

The Dot Product
The Dot Product In this section, we will now concentrate on the vector operation called the dot product. The dot product of two vectors will produce a scalar instead of a vector as in the other operations that we examined in the previous section. The dot product is equal to the sum of the product of the horizontal components and the product of the vertical components. If v = a1 i + b1 j and w = a2 i + b2 j are vectors then their dot product is given by: v · w = a1 a2 + b1 b2 Properties of the Dot Product If u, v, and w are vectors and c is a scalar then: u · v = v · u u · (v + w) = u · v + u · w 0 · v = 0 v · v = || v || 2 (cu) · v = c(u · v) = u · (cv) Example 1: If v = 5i + 2j and w = 3i – 7j then find v · w. Solution: v · w = a1 a2 + b1 b2 v · w = (5)(3) + (2)(-7) v · w = 15 – 14 v · w = 1 Example 2: If u = –i + 3j, v = 7i – 4j and w = 2i + j then find (3u) · (v + w). Solution: Find 3u 3u = 3(–i + 3j) 3u = –3i + 9j Find v + w v + w = (7i – 4j) + (2i + j) v + w = (7 + 2) i + (–4 + 1) j v + w = 9i – 3j Example 2 (Continued): Find the dot product between (3u) and (v + w) (3u) · (v + w) = (–3i + 9j) · (9i – 3j) (3u) · (v + w) = (–3)(9) + (9)(-3) (3u) · (v + w) = –27 – 27 (3u) · (v + w) = –54 An alternate formula for the dot product is available by using the angle between the two vectors. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential