Informatik-Affine Themen in Der Didaktik Der Mathematik
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Aboard the Impulse Train: an Analysis of the Two- Channel Title Music Routine in Manic Miner Kenneth B
All aboard the impulse train: an analysis of the two- channel title music routine in Manic Miner Kenneth B. McAlpine This is the author's accepted manuscript. The final publication is available at Springer via http://dx.doi.org/10.1007/s40869-015-0012-x All Aboard the Impulse Train: An analysis of the two-channel title music routine in Manic Miner Dr Kenneth B. McAlpine University of Abertay Dundee Abstract The ZX Spectrum launched in the UK in April 1982, and almost single- handedly kick-started the British computer games industry. Launched to compete with technologically-superior rivals from Acorn and Commodore, the Spectrum had price and popularity on its side and became a runaway success. One area, however, where the Spectrum betrayed its price-point was its sound hardware, providing just a single channel of 1-bit sound playback, and the first-generation of Spectrum titles did little to challenge the machine’s hardware. Programmers soon realised, however, that with clever machine coding, the Spectrum’s speaker could be encouraged to do more than it was ever designed to. This creativity, borne from constraint, represents a very real example of technology, or rather limited technology, as a driver for creativity, and, since the solutions were not without cost, they imparted a characteristic sound that, in turn, came to define the aesthetic of ZX Spectrum music. At the time, there was little interest in the formal study of either the technologies that support computer games or the social and cultural phenomena that surround them. This retrospective study aims to address that by deconstructing and analysing a key turning point in the musical life of the ZX Spectrum. -

CLONE WARS Get a Brazilian
April 2018 Issue 21 PLUS CLONE WARS Get a Brazilian.. Includes material MIND YOUR LANGUAGE not in the video Continued programming show! feature CONTENTS 16. CLONE WARS The Brazilian clones explored. 22. MIND YOUR LANGUAGE 12. OMNI 128HQ Spectrum languages. A new Speccy arrives. FEATURES GAME REVIEWS 4 News from 1987 Knight Lore 6 Find out what was happening back in 1987. Elixir Vitae 8 12 Isometric Games Grand Prix Championship 9 Knightlore and more. Viagem ao Centro da terra 14 16 Clone Wars Exploration of the Brazilian clones. Kung Fu Knights 20 24 Mind Your Language Sewer Rage 21 More languages from George. Dominator 22 32 Play Blackpool Report from the recent event. Spectres 23 36 Vega Games Wanted: Monty Mole 30 Games without instructions on the Vega. 3D Tunnel 31 38 Grumpy Ogre Retro adventuring and championship moaning. Gauntlet 34 42 Omni 128HQ Laptop A new Spectrum arrives. And more…. Page 2 www.thespectrumshow.co.uk EDITORIAL elcome to issue 21 and thank you W I was working on several things at the for taking the time to download and same time on two different comput- read it. ers. I was doing some video editing on As series seven of The Spectrum Show my main PC and at the same time checking emails and researching fu- comes to an end with a mammoth end say, I am impressed with it. It’s a Har- ture features on my little Macbook Air. of series special, the next series is al- lequin (Spectrum modern clone) main ready well underway in the planning Strangely, both required an update, so board fitted inside a new 48K style stages. -
Page 1 of 4 Sinclair ZX80 Computer 1/24/2013
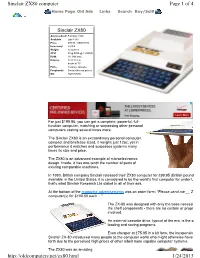
Sinclair ZX80 computer Page 1 of 4 Home Page Old Ads Links Search Buy/Sell! Sinclair ZX80 Anouncedced: February 1980 Available: Late 1980 Price: £99.95 / US$199.95 How many: 50,000 Weight: 12 ounces CPU: Zilog Z80A @ 3.25MHz RAM: 1K, 64K max Display: 22 X 32 text hooks to TV Ports: memory, cassette Peripherals: Sinclair thermal printer OS: ROM BASIC For just $199.95, you can get a complete, powerful, full- function computer, matching or surpassing other personal computers costing several times more. The Sinclair ZX80 is an extraordinary personal computer, compact and briefcase sized, it weighs just 12oz, yet in performance it matches and surpasses systems many times its size and price. The ZX80 is an advanced example of microelectronics design. Inside, it has one-tenth the number of parts of existing comparable machines. In 1980, British company Sinclair released their ZX80 computer for £99.95 (British pound available in the United States, it is considered to be the world's first computer for under U that's what Sinclair Research Ltd stated in all of their ads. At the bottom of the magazine advertisements was an order form: "Please send me __ ZX computer(s) for $199.95 each ..." The ZX-80 was designed with only the base necessit the shelf components - there are no custom or propri involved. An external cassette drive, typical of the era, is the o loading and saving programs. Even cheaper at £75.95 in a kit form, the inexpensive Sinclair ZX-80 introduced many people to the computer world who might otherwise have forth due to the perceived high prices of other albeit more capable computer systems. -

Issue #1 August 2015 Zxzine Table of Contents
zxzine Issue #1 August 2015 zxzine table of contents Published by: Timothy Swenson [email protected] [email protected] Editorial .......................... 1 ZXzine is published as a service to the Sinclair ZX81 community. Writers are invited to submit articles for publication. Readers The ZX80 and ZX81 are invited to submit article In The USA ........................... 1 ideas. Created using Open Source Tools: Plotting with Z88dk ........................... 5 OpenOffice Scribus Gimp SZ81 EightyOne ZX81 BASIC Compilers ........................... 6 Copyright 2015 Timothy Swenson Drawing a Line ........................... 8 Creative Commons License Attribution NonCommercial ShareAlike Astronomical Algorithms On You are free: The ZX81 ........................... 9 To copy, distribute, display, and perform the work. MicroSync Services ........................... 10 To make derivitive works. To redistribute the work. Editorial doing right. Ideas for article is invited, along with articles themselves. The topics of articles can be I've been a ZX81 user since the first was advertised anything that is ZX81 related. I'm hoping that the in the United States and used it for a number of ZX81 community will find the ezine interesting, years, including using it as much as I could in my entertaining and useful. first two years of college. Eventually moved on to the QL, but still liked the ZX81. A few years ago, I had the programming itch and decided to do a little The ZX80 and ZX81 assembly programming using emulators and ZX81 in the USA cross assemblers. Since then I've touched on C with Z88dk. What I like about the ZX81 is that I don't Sinclair Research Limited have to spend any time worrying about the user interface or making the program pretty. -

Didaktik Gama 192 Editoriale
Periodico di informazione sul mondo Sinclair e Spectrum N°4 Agosto - Settembre 2004 Copyleft 2004 Stefano Guida autore ed editore In questo numero: 1 - Didaktik Gama 192 Editoriale 2 - Spectrum... di sinistra? L'estate e' arrivata e come tutti Didaktik Gama che e' l'occasione come sempre per 2 - ZX81 gli anni, in questo periodo, le disponibile ad una cifra piuttosto ricordare a tutti voi che se volete 3 - Compatibilita' ZX Spectrum notizie e le novità ovviamente modica; ci sara' uno spazio scrivere un articolo per questa e altri cloni scarseggiano per poi riprendere dedicato alle curiosità alcune rivista potete farlo inviandolo 3 - Sir Clive ci riprova a pieno ritmo all'inizio delle quali anche divertenti, all'indirizzo: dell'autunno. articoli presi da internet e [email protected] . 3 - Vinili per Spectrum In questo numero affronteremo addirittura uno scritto da un Verrà pubblicato sul prossimo quindi gli argomenti che in appassionato lettore di questa numero con tanto di 4 - Minigame 2004 questi ultimi mesi hanno stessa rivista autore di un ringraziamenti per la 4 - Nuovi cloni popolato il web parlando anche programma molto utile nella collaborazione. dello ZX81. Una particolare gestione dei nastri ormai S.G. 4 - Damtape attenzione va al nuovo clone del deteriorati. Colgo quindi [email protected] 5 - Collegare un +2A/+3 via Scart 5 - QL Neeting 2004 5 - Mistrum Didaktik Gama 192 6 - Strane periferiche Come annunciato nel numero precedente, una Didaktik (che attualmente produce alcuni articoli 6 - Il clone del mese delle novità più discusse recentemente è il di componentistica e controllori di processi) alla 6 - Vignetta & ringraziamenti Didaktik Gama 192K. -

Vysoke´Ucˇenítechnicke´V Brneˇ
VYSOKE´ UCˇ ENI´ TECHNICKE´ V BRNEˇ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA INFORMACˇ NI´CH TECHNOLOGII´ U´ STAV POCˇ ´ITACˇ OVY´ CH SYSTE´ MU˚ FACULTY OF INFORMATION TECHNOLOGY DEPARTMENT OF COMPUTER SYSTEMS EMULA´TOR MALE´ HO DOMA´ CI´HO POCˇ ´ITACˇ E ZX SPECTRUM DIPLOMOVA´ PRA´ CE MASTER’S THESIS AUTOR PRA´ CE Bc. PETR Sˇ IMON AUTHOR BRNO 2012 VYSOKE´ UCˇ ENI´ TECHNICKE´ V BRNEˇ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA INFORMACˇ NI´CH TECHNOLOGII´ U´ STAV POCˇ ´ITACˇ OVY´ CH SYSTE´ MU˚ FACULTY OF INFORMATION TECHNOLOGY DEPARTMENT OF COMPUTER SYSTEMS EMULA´TOR MALE´ HO DOMA´ CI´HO POCˇ ´ITACˇ E ZX SPECTRUM ZX SPECTRUM SMALL HOME COMPUTER EMULATOR DIPLOMOVA´ PRA´ CE MASTER’S THESIS AUTOR PRA´ CE Bc. PETR Sˇ IMON AUTHOR VEDOUCI´ PRA´ CE Ing. RICHARD RU˚ Zˇ ICˇ KA, Ph.D. SUPERVISOR BRNO 2012 Abstrakt Osmibitový počítač ZX Spectrum vznikl pøed 30 lety. Ve své době zažil obrovský úspěch a dodnes má poèetnou základnu příznivcù, kteří stále vytvářejí nové aplikace a hry. Vznikají v¹ak i nová hardwarová rozšíření pro pøipojení moderních periferií, jako jsou IDE HDD, paměťové karty apod. Tato práce si dává za cíl navrhnout a postavit emulátor počítače ZX Spectrum, který bude založen na moderní technologii FPGA a bude používat moderní periferie jako VGA monitor, SD/MMC paměťové karty apod. Abstract Eight-bit computer ZX Spectrum has been created 30 years ago. It was extremely popular in its time and it has many fans till now, which still developing new application and games. There are also many new hardware extensions like IDE HDD driver, SD/MMC memory driver etc. -

OF the 1980S
THAT MADE THE HOME COMPUTER REVOLUTION OF THE 1980s 23 THAT MADE THE HOME COMPUTER REVOLUTION OF THE 1980s First published in 2021 by Raspberry Pi Trading Ltd, Maurice Wilkes Building, St. John’s Innovation Park, Cowley Road, Cambridge, CB4 0DS Publishing Director Editors Russell Barnes Phil King, Simon Brew Sub Editor Design Nicola King Critical Media Illustrations CEO Sam Alder with Brian O Halloran Eben Upton ISBN 978-1-912047-90-1 The publisher, and contributors accept no responsibility in respect of any omissions or errors relating to goods, products or services referred to or advertised in this book. Except where otherwise noted, the content of this book is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported (CC BY-NC-SA 3.0). Contents Introduction. 6 Research Machines 380Z. 8 Commodore PET 2001. 18 Apple II. 36 Sinclair ZX80 and ZX81. 46 Commodore VIC-20 . 60 IBM Personal Computer (5150). 78 BBC Micro . 90 Sinclair ZX Spectrum. 114 Dragon 32. 138 Commodore 64. 150 Acorn Electron . .166 Apple Macintosh . .176 Amstrad CPC 464. 194 Sinclair QL . .210 Atari 520ST. 222 Commodore Amiga. 234 Amstrad PCW 8256. 256 Acorn Archimedes . .268 Epilogue: Whatever happened to the British PC? . .280 Acknowledgements . 281 Further reading, further viewing, and forums. 283 Index . .286 The chapters are arranged in order of each computer’s availability in the UK, as reflected by each model’s date of review in Personal Computer World magazine. Introduction The 1980s was, categorically, the best decade ever. Not just because it gave us Duran Duran and E.T., not even because of the Sony Walkman. -

How 1980S Britain Learned to Love the Computer
Lean, Tom. "Computers for the Man in the Street." Electronic Dreams: How 1980s Britain Learned to Love the Computer. London: Bloomsbury Sigma, 2016. 61–88. Bloomsbury Collections. Web. 30 Sep. 2021. <http://dx.doi.org/10.5040/9781472936653.0006>. Downloaded from Bloomsbury Collections, www.bloomsburycollections.com, 30 September 2021, 11:40 UTC. Copyright © Tom Lean 2016. You may share this work for non-commercial purposes only, provided you give attribution to the copyright holder and the publisher, and provide a link to the Creative Commons licence. CHAPTER THREE Computers for the Man in the Street arly in 1980, adverts began appearing in British newspapers Efor something rather unusual. Sandwiched between pages of economic and social troubles, Thatcherite politics and Cold War paranoia was an advert for a small white box. It looked a little like an overgrown calculator, but declared itself to be the Sinclair ZX80 Personal Computer, and could be bought, ready made, for just £ 99.95. Despite the implausibly low price, the ZX80 was not only a ‘ real computer ’ , but one that cut through computer ‘ mystique ’ to teach programming, and was so easy to use that ‘ inside a day you ’ ll be talking to it like an old friend’ , or so the advert said. It was an impressively crafted piece of marketing, creating an impression of aff ordability and accessibility, ideas hitherto rarely associated with computers. The little white box, and the bold claims that sold it, marked the beginning of a redefi nition of computers as aff ordable and everyday appliances for the masses. At the time microcomputers were broadly split between two basic types. -

Greenstreet Publisher
ZXF05: 31 PRICE LIST (prices checked 30 March 2003) Top tips for using PAW with an emulator New hardware: PC-PSU with supply for 2 Floppies and MB02 36,00 € 'overlays,' as they were called - Use an emulator. You probably were going to anyway, but just in case MB02-Printerlead 13,00 € to add extra features to the you were tempted to go for the 'performance art' process of using real Spectrum +2A, new and original package, complete 219,00 € system was included. Essentially hardware, consider the pain of having to SAVE and VERIFY your Proface AT Extern (Interface for connecting PC-Keyboards to Spectrum) 69,00 € KS a modular system anyway (48K adventure game database each time you end a PAW session with the Proface AT Intern (internal interface) 62,00 € KS users didn't get the whole system simplicity of a quick snapshot save. at once and had to load in and Melodik AY-Soundbox (unboxed) 24,00 € KS Speed up your emulator to about 300 per cent to speed up the entry of out of memory the various +2 Cassette recorder 36,00 € long text passages (the cursor gets slower... and... slower... the more you modules - location text, process Floppy Disc drive (1,86 with MB02, 720k with Opus, 780k with +D) Please specify 24,00 € type). Any faster though and key presses might be missed. Speed it up tables, etc - as required, which all the way when using the text compressor, however. PSU for +2A/B and +3 or PSUl for +2 (also 48k and 128k) Please specify 29,00 € must have been a chore), the FDD lead for 2 drives 4,00 € potential for these was Run two seperate emulator windows - one for editing, the other for Multiface 128 (works also on 48k Spectrums 26,00 € enourmous, but the only testing; alternatively you could use two seperate emulators. -

ZXF08.Pdf Download
08 Spectrum computing today www.cwoodcock.co.uk/zxf PRICE LIST (prices checked 20 April 2004) New: PC-PSU with supply for 2 Floppies and MB02 36,00 € MB02-Printerlead 13,00 € Proface AT Extern (Interface for connecting PC-Keyboards to Spectrum) 69,00 € KS Proface AT Intern (internal interface) 62,00 € KS Melodik AY-Soundbox (unboxed) 24,00 € KS +2 Cassette recorder 36,00 € Floppy Disc drive (1,86 with MB02, 720k with Opus, 780k with +D) Please specify 24,00 € PSU for +2A/B and +3 or PSUl for +2 (also 48k and 128k) Please specify 29,00 € FDD lead for 2 drives 4,00 € Multiface 128 (works also on 48k Spectrums 26,00 € Dust Cover 48k+/128k 8,00 € Plus 3 Tapelead 9,90 € Normal Tapelead 3,00 € Spectrum +2 Lightpen 36,00 € Spectrum +3 Lightpen 27,00 € Phaser Gun with Software (Tape or +3) 19,00 € SCART-Monitor cable (choose for 128k/+2 or +2A/+3) 25,00 € VGA-BOX (connect Spectrum 128/+2 to VGA monitor) 49,00 € VGA-BOX Multi purpose (Connect any PC monitor to Spectrum 128/+2) 79,00 € +3 drive belt 2,00 € Silver paper for ZX Printer 5,00 € Keyboard membrane 48k 11,00 € Keyboard membrane Spectrum +/128k, new quality, not aging 21,00 € Spectrum keyword stickers 8,00 € Used: Sinclair ZX Spectrum 128k, complete with all cables 129,00 € Sinclair ZX Spectrum +2, complete with all cables 79,00 € Sinclair ZX Spectrum +2A, complete with all cables 69,00 € Sinclair ZX Spectrum +3, built in 3'' drive, complete with all cables 99,00 € Sinclair Spectrum 48k (Gummy), complete with all cables + Introduction Tape 64,00 € Sinclair Spectrum 48k +, complete with all cables + Introduction Tape 64,00 € +3 Drive (tested) 29,00 € Interface I 69,00 € Microdrive 25,00 € Wafadrive 39,00 € Opus Discovery Diskinterface with 1 x 720k Drive (new ROM) 119,00 € Joystick interface 1-Port 3,00 € 2-Port 11,00 € Joystick (many different) 2,50 € Sinclair SJS-Joystick (+2/+3) 6,00 € Consumables: Microdrive Cartridges (ex-software) 3,50 € Wafadrive Cartridges 16K= 7,00 €, 32K= 7,50 € Also we have a lot of Software offers and books. -

Micro Computing
Micro computing Thomas J. Bergin ©Computer History Museum American University Context…. • What was going on in the computer industry in the 1970s? – Mainframes and peripherals – Minicomputers and peripherals – Telecommunications – Applications, applications, applications – Operating systems and programming languages And the answer is…. • Everything!!! – Mainframes from small to giant – Supercomputers (many varieties) – Minicomputers, Super Minis, tiny Minis – Networks, WANS, LANS, etc. – Client Server Architectures – 2nd and 3rd generation applications: • Executive Information Systems • Decision Support Systems, etc. And into this technologically rich soup of computing, comes the: • Microprocessor • Microcomputer • New Operating Systems • New Operating Environments • Economics • New Users, New Users, New Users, New Users, New Users, New Users, New Users Intel • Robert Noyce, Gordon Moore, and Andrew Grove leave Fairchild and found Intel in 1968 – focus on random access memory (RAM) chips • Question: if you can put transistors, capacitors, etc. on a chip, why couldn’t you put a central processor on a chip? Enter the hero: Ted Hoff • Ph.D. Stanford University: Electrical Engineering – Semiconductor memories; several patents • Intel's 12th employee: hired to dream up applications for Intel's chips • Noyce wanted Intel to do memory chips only! • 1969: ETI, a Japanese calculator company -- wants a chip for a series of calculators The Microprocessor • ETI calculator would cost as much as a mini • "Why build a special purpose device when a general purpose device would be superior?" • Hoff proposed a new design loosely based on PDP-8: the Japanese weren't interested! • October 1969, Japanese engineers visit Intel to review the project, and agree to use the I 4004 for their calculator. -

1900 (Parents: 769, Clones: 1131)
Supported systems: 1900 (parents: 769, clones: 1131) Description [ ] Name [ ] Parent [ ] Year [ ] Manufacturer [ ] Sourcefile [ ] 1200 Micro Computer shmc1200 studio2 1978 Sheen studio2.c (Australia) 1292 Advanced Programmable Video 1292apvs 1976 Radofin vc4000.c System 1392 Advanced Programmable Video 1392apvs 1292apvs 1976 Radofin vc4000.c System 15IE-00-013 ie15 1980 USSR ie15.c 286i k286i ibm5170 1985 Kaypro at.c 3B1 3b1 1985 AT&T unixpc.c 3DO (NTSC) 3do 1991 The 3DO Company 3do.c 3DO (PAL) 3do_pal 3do 1991 The 3DO Company 3do.c 3DO M2 3do_m2 199? 3DO konamim2.c 4004 Nixie Clock 4004clk 2008 John L. Weinrich 4004clk.c 486-PIO-2 ficpio2 ibm5170 1995 FIC at.c 4D/PI (R2000, 20MHz) sgi_ip6 1988 Silicon Graphics Inc sgi_ip6.c 6809 Portable d6809 1983 Dunfield d6809.c 68k Single Board 68ksbc 2002 Ichit Sirichote 68ksbc.c Computer 79152pc m79152pc ???? Mera-Elzab m79152pc.c 800 Junior elwro800 1986 Elwro elwro800.c 9016 Telespiel mtc9016 studio2 1978 Mustang studio2.c Computer (Germany) A5120 a5120 1982 VEB Robotron a51xx.c A5130 a5130 a5120 1983 VEB Robotron a51xx.c A7150 a7150 1986 VEB Robotron a7150.c Aamber Pegasus pegasus 1981 Technosys pegasus.c Aamber Pegasus with pegasusm pegasus 1981 Technosys pegasus.c RAM expansion unit ABC 1600 abc1600 1985 Luxor abc1600.c ABC 80 abc80 1978 Luxor Datorer AB abc80.c ABC 800 C/HR abc800c 1981 Luxor Datorer AB abc80x.c ABC 800 M/HR abc800m abc800c 1981 Luxor Datorer AB abc80x.c ABC 802 abc802 1983 Luxor Datorer AB abc80x.c ABC 806 abc806 1983 Luxor Datorer AB abc80x.c Acorn Electron electron 1983