Comparison of Results from Turbulence Models for the Nomad Flaperon
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Outlook V37 N2 March 2021 Draft Portrait
Outlook / AHSA News Vol. 37 No. 3 June 2021 Outlook A.H.S.A. AHSA News Vol. 37 No. 3 June 2021 This edi�on of Outlook comes to readers in the middle of winter - and this photograph of Anse�-ANA’s Douglas DC-6B VH-INU (c/n 44694-558) from the Peter Kelly collec�on was taken on an overcast and wet day, typical of what might be expected in a Melbourne winter. But in fact the photograph was taken at Essendon on December 15th 1966. Newsletter of the Website: Aviation Historical www.ahsa.org.au Society of Australia, Inc. A0033653P Facebook Group: ARBN 092-671-773 www.facebook.com/groups/AHSAustPage 1 Outlook / AHSA News Vol. 37 No. 3 June 2021 Avia�on Historical Society of Australia Inc. What’s Inside? President’s Comment 2 Our 2020/21 Commi�ee: AHSA news 3 President: Dave Prossor Civil Avia�on Centenary Update 6 [email protected] Civil Avia�on Snippets 6 RAAF Centenary Update 10 Vice-President: Derek Buckmaster [email protected] Military Avia�on Snippets 12 Australian Industry News Snippets 15 Secretary: Mark Pilkington Coming Avia�on Events 16 [email protected] Museum News 16 Treasurer: Robert Van Woerkom New books on Australian Avia�on History 18 [email protected] Research Corner 20 Membership David Knight Secretary: [email protected] President’s Comment Commi�ee Members: For a start I would like to think that AHSA readers enjoyed the GPCAPT David Fredericks last issue of the newsle�er. A different style and content being Dion Makowski driven by the current commi�ee. -

Computer and Information Science, ISSN 1913-8989, Vol. 1, No. 1
Vol. 1, No. 1 Computer and Information Science Mapping of Power Transmission Lines on Malaysian Highways Using UPM-APSB’s AISA Airborne Hyperspectral Imaging System Hj. Kamaruzaman Jusoff Forest Geospatial Information & Survey Lab, Lebuh Silikon Faculty of Forestry, Universiti Putra Malaysia Serdang 43400 Selangor, Malaysia Tel: +60-3-8946 7176 E-mail: [email protected] Norsuzila Ya’acob Faculty of Electrical Engineering, Universiti Teknologi MARA UiTM 40450 Shah Alam, Malaysia Tel: +60-3-5544 2000 E-mail: [email protected] Abstract Power transmission lines routes mapping is an important technique for locating power transmission line routes and towers on mountain/hilltops to assist viewing of their impacts on the environment, operations and allocation of public utilities. A study was therefore conducted to map the power transmission lines within Bukit Lanjan PLUS highway. The main objective of this study is to assess the capability of airborne hyperspectral sensing for mapping of power transmission. By using ENVI software, the airborne hyperspectral imaging data was enhanced using convolution filtering technique using band 3 which produced a gray scale image which appeared clearer and sharper. The spectral reflectance curves were acquired for each power line which showed the same spectrum characteristics in curve or the reflectance energy. This is because of the same power lines composition material for all power lines. Ground verification was done by comparing the UPM-APSB’s AISA Global Positioning System (GPS) coordinates readings with ground GPS coordinates readings of the power transmission lines footings. The ground verification result from the two matching power transmission line footings showed that the accuracy of power lines identification was acceptable. -

Falco Builders Letter
Falco Builders Letter A Visit with Frati If anybody ever suggests you go visit Frati “in Milan,” as Alfred Scott did when he heard I was going to be in Italy writing about the Piaggio Avanti turboprop, here’s my suggestion: get Alfred to pay the cabfare. If you can’t do that, buy a car. A small Fiat will do, and it’ll prob- ably be cheaper than a cab. I leapt off the train from Genoa at Milan’s central station and plunged straight into a waiting taxi. “Via Trieste Vente-Quat- tro,” I said in my best non-Italian, and about $15 later, that’s exactly where he took me—24 Via Trieste. Quiet urban residential street... relatively upscale... odd place for an airplane factory.... Actually, there was no number 24. We found a phone booth, and my cabbie Jim and Gail Martin's Falco is the 17th Sequoia Falco to fly. was nice enough to tackle the Italian telephone system on my behalf. He First Flight: Around the Falco called Frati’s number, and I knew I was in trouble when I saw him perform the Jim and Gail Martin Patch classic application of heel of hand smartly Jim and Gail Martin’s Falco flew for Luciano Nustrini came to Oshkosh as to forehead, as though trying to jar loose a the first time on August 13th in But- planned, but not via Europe as he had subdural hematoma: the Via Trieste that ler, Pennsylvania, making it the 17th intended. There was a change in plans, I wanted, it turned out—a street that ap- Sequoia Falco to fly. -

Killers in Aviation: FSF Task Force Presents Facts About Approach-And-Landing and Controlled-Flight-Into-Terrain Accidents
FLIGHT SAFETY FOUNDATION NOVEMBER–DECEMBER 1998 JANUARY–FEBRUARY 1999 FLIGHT SAFETY DIGEST Killers in Aviation: FSF Task Force Presents Facts About Approach-and-landing and Controlled-flight-into-terrain Accidents Special FSF Report FLIGHT SAFETY FOUNDATION For Everyone Concerned Flight Safety Digest With the Safety of Flight Vol. 17 No. 11–12 November–December 1998 Officers and Staff Vol. 18 No. 1–2 January–February 1999 Stuart Matthews US$80.00 (members) US$120.00 (nonmembers) Chairman, President and CEO Board of Governors James S. Waugh Jr. Treasurer In This Issue Carl Vogt General Counsel and Secretary Killers in Aviation: FSF Task Force Presents Board of Governors Facts about Approach-and-landing and 1 ADMINISTRATIVE Controlled-flight-into-terrain Accidents Nancy Richards This special report includes the most recent versions of working- Executive Secretary group reports from the FSF Approach-and-landing Accident Ellen Plaugher Reduction (ALAR) Task Force, as well as previously published Executive Support–Corporate Services reports that also include data about controlled -flight-into-terrain (CFIT) accidents. These combined reports present a unique and FINANCIAL comprehensive review of ALAs and CFIT. Elizabeth Kirby Controller 1997 Fatal-accident Rates among Aircraft in TECHNICAL Scheduled Services Increased, but 257 Robert H. Vandel Director of Technical Projects Passenger-fatality Rate Decreased Jim Burin The International Civil Aviation Organization said that the 1997 Deputy Director of Technical Projects passenger-fatality rate for turbojet aircraft was substantially Robert H. Gould lower than the passenger-fatality rates for propeller-driven Managing Director of Aviation Safety Audits aircraft. and Internal Evaluation Programs Robert Feeler Standards for Engineered-materials Manager of Aviation Safety Audits Arresting Systems Aim to Provide 260 Robert Dodd, Ph.D. -

The Lockheed Era
Vol. XVI No. 3 July—August, 1975 Price $1.55 Registered for posting as a periodical Category B. Aviation Historical Society OF Australia TOURNAL Founded 1959 D The Lockheed Era :||ii wiws I I Guinea Airways Lockheed 10A VH—UXH at Mascot Aerodrome. P.J. Ricketts H WllMiiiilii Ansett's Lockheed 10B VH—UZP "Ansalanta" at Mascot. via. F. Walters iiiil m ife>iIII Guinea Airways Lockheed 10A VH-UXI at Mascot. Reddall Collection Guinea Airways Lockheed 10A VH-UXH at Mascot. P.J. Ricketts AVIATION HISTORICAL SOCIETY OF AUSTRALIA JOURNAL -29- Vol. XVI No. 3 July—August 1975 Patron: Sir Donald Anderson CBE President: Dr. L.V. Turner THE LOCKHEED ERA by G. Goodall Vice President: R.J. Gibson Secretary: G.H. Stone The Civil Use of Lockheed 10-18 Series in Australia Treasurer: P.J. Ricketts Journal Distribution: C.H. O'Neill (This is the first of a series of three articles on this subject by the author. Journal Editors: P.J. Ricketts F. Walters The remaining two parts will be published in later Journals) Photo Pages - Layout J. Gallagher A sleek pale blue Lockheed 12A parked on the grass at Sydney's Movements: E.S. Favelle Bankstown Airport, and a portly orange blue and white Lockheed Hudson parked Register Editor: J.L. Bell on the apron at Tamworth Airport in northern NSW are the two remaining air Museum Notes: P.N. Anderson worthy examples In Australia of a line of transport aircraft that are just as signi Contributors: ficant to this country's aviation history as the Douglas DC-3. -

Police Aviation News August 2011
Police Aviation News August 2011 ©Police Aviation Research Number 184 August 2011 PAR Police Aviation News August 2011 2 PAN—Police Aviation News is published monthly by POLICE AVIATION RESEARCH, 7 Wind- mill Close, Honey Lane, Waltham Abbey, Essex EN9 3BQ UK. Contacts: Main: +44 1992 714162 Cell: +44 7778 296650 Skype: BrynElliott E-mail: [email protected] SPONSORS AgustaWestland www.agustawestland.com Bob Crowe www.bobcroweaircraft.com Broadcast Microwave www.downlinkexperts.com CurtissWright Controls www.skyquest.com Diamond Aircraft www.diamond-air.at Enterprise Control Systems www.enterprisecontrol.co.uk Honeywell [Skyforce] Mapping www.skyforce.co.uk L3 Wescam www.wescam.com Powervamp www.powervamp.com Troll Downlinks www.trollsystems.com Zeiss Optronics www.zeiss.com/optronics Airborne Law Enforcement Association www.alea.org European Law Enforcement Association www.pacenet.info LAW ENFORCEMENT AUSTRALIA QUEENSLAND: It has been a long time coming but finally it seems that the State of Queensland is going to set up a proper helicopter trial. Back in July 2003 Galen Gunn a helicopter pilot in Australia for over 10 years running a business engaged in providing survey services to the government worked with the Police in Queensland to provide them with a airborne platform for their security needs mainly relating to the world cup rugby that year. Gunn sought the help of ALEA in the USA to get the equip- ment and an MD500 helicopter together. The operation used a pre-owned [ex-North Wales Police UK] Wescam sensor and was seeking other options after the trial via ALEA but there was no longer term activity. -
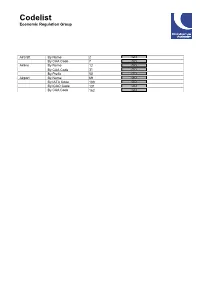
G:\JPH Section\ADU CODELIST\Codelist.Snp
Codelist Economic Regulation Group Aircraft By Name By CAA Code Airline By Name By CAA Code By Prefix Airport By Name By IATA Code By ICAO Code By CAA Code Codelist - Aircraft by Name Civil Aviation Authority Aircraft Name CAA code End Month AEROSPACELINES B377SUPER GUPPY 658 AEROSPATIALE (NORD)262 64 AEROSPATIALE AS322 SUPER PUMA (NTH SEA) 977 AEROSPATIALE AS332 SUPER PUMA (L1/L2) 976 AEROSPATIALE AS355 ECUREUIL 2 956 AEROSPATIALE CARAVELLE 10B/10R 388 AEROSPATIALE CARAVELLE 12 385 AEROSPATIALE CARAVELLE 6/6R 387 AEROSPATIALE CORVETTE 93 AEROSPATIALE SA315 LAMA 951 AEROSPATIALE SA318 ALOUETTE 908 AEROSPATIALE SA330 PUMA 973 AEROSPATIALE SA341 GAZELLE 943 AEROSPATIALE SA350 ECUREUIL 941 AEROSPATIALE SA365 DAUPHIN 975 AEROSPATIALE SA365 DAUPHIN/AMB 980 AGUSTA A109A / 109E 970 AGUSTA A139 971 AIRBUS A300 ( ALL FREIGHTER ) 684 AIRBUS A300-600 803 AIRBUS A300B1/B2 773 AIRBUS A300B4-100/200 683 AIRBUS A310-202 796 AIRBUS A310-300 775 AIRBUS A318 800 AIRBUS A319 804 AIRBUS A319 CJ (EXEC) 811 AIRBUS A320-100/200 805 AIRBUS A321 732 AIRBUS A330-200 801 AIRBUS A330-300 806 AIRBUS A340-200 808 AIRBUS A340-300 807 AIRBUS A340-500 809 AIRBUS A340-600 810 AIRBUS A380-800 812 AIRBUS A380-800F 813 AIRBUS HELICOPTERS EC175 969 AIRSHIP INDUSTRIES SKYSHIP 500 710 AIRSHIP INDUSTRIES SKYSHIP 600 711 ANTONOV 148/158 822 ANTONOV AN-12 347 ANTONOV AN-124 820 ANTONOV AN-225 MRIYA 821 ANTONOV AN-24 63 ANTONOV AN26B/32 345 ANTONOV AN72 / 74 647 ARMSTRONG WHITWORTH ARGOSY 349 ATR42-300 200 ATR42-500 201 ATR72 200/500/600 726 AUSTER MAJOR 10 AVIONS MUDRY CAP 10B 601 AVROLINER RJ100/115 212 AVROLINER RJ70 210 AVROLINER RJ85/QT 211 AW189 983 BAE (HS) 748 55 BAE 125 ( HS 125 ) 75 BAE 146-100 577 BAE 146-200/QT 578 BAE 146-300 727 BAE ATP 56 BAE JETSTREAM 31/32 340 BAE JETSTREAM 41 580 BAE NIMROD MR. -

Fishermans Bend In-Depth Heritage Review and Stakeholder Engagement
City of Melbourne Fishermans Bend In-Depth Heritage Review and Stakeholder Engagement Summary Report February 2021 Prepared by Helen Lardner, Architect, Director HLCD Pty Ltd Total House L8, 180 Russell St Melbourne VIC 3122 With Dr Peter Mills Historian Prepared for City of Melbourne Project Owner: Ms Tanya Wolkenberg Project Manager: Ms Molly Wilson Contents 1 Executive Summary ......................................................................................................... 1 2 The Study .......................................................................................................................... 3 2.1 Introduction.................................................................................................................. 3 2.2 Scope .......................................................................................................................... 4 2.3 Mechanisms Available to Protect Heritage ................................................................. 5 3 Methodology ..................................................................................................................... 5 3.1 Review of Existing Studies and Strategies ................................................................. 5 3.2 Historical Research ..................................................................................................... 6 3.3 Site Inspections ........................................................................................................... 7 3.4 Further Analysis ......................................................................................................... -

Warsaw Chopin Airport Quota System Table
WARSAW CHOPIN AIRPORT QUOTA SYSTEM TABLE No Aircraft type IATA Arrival Departure Code QC points QC points 1. Fokker 100 100 0,25 0,5 2. Hawker Siddeley HS125 H25 2 8 3. BAe 146-100 141 0,5 0,5 4. BAe 146-200 142 0,25 0,25 5. BAe 146-300 143 0,5 0,5 6. BAe 146 146 0,5 0,5 7. BAe 146 Freighter 14F 0,5 0,5 8. BAe 146 Freighter 14X 0,25 0,25 9. BAe 146 Freighter 14Y 0,25 0,25 10. BAe 146 Freighter 14Z 0,25 0,25 11. Airbus A310 310 1 2 12. Airbus A310-200 312 1 2 13. Airbus A310-300 313 1 2 14. Airbus A318 318 0,25 0,25 15. Airbus A319 319 0,25 0,5 16. Airbus A310-200F 31X 1 2 17. Airbus A310-300F 31Y 1 2 18. Airbus A320-100/200 320 0,5 1 19. Airbus A321-100/200 321 0,5 2 20. Airbus A320 (winglets) 32A 0,5 1 21. Airbus A319/A320/A321 32S 0,5 2 22. Airbus A330 330 0,5 2 23. Airbus A330-200 332 0,5 2 24. Airbus A330-300 333 0,5 2 25. Airbus A340 340 1 2 26. Airbus A340-200 342 0,5 2 27. Airbus A340-300 343 0,5 2 28. Airbus A340-500 345 1 2 29. Airbus A340-600 346 1 2 30. Airbus A380 380 0,5 2 31. Airbus A380-800 388 0,5 2 32. -

Accidents/Incidents for 2006
Safety review Accidents/incidents for 2006 Notes on tables Accident data comes from Flight International’s own research, sister online International continues to list as many incidents as possible, in the inter- publication Air Transport Intelligence and from Flight’s database service ests of maximising the availability of relevant information. Consequently, Acas’s daily occurrence information. Details of non-fatal incidents are not we accept the non-fatal listing may be weighted against the airlines of made available offi cially by the authorities in many countries, but Flight those countries that make safety information more readily available. GLOSSARY OF TERMS AND ABBREVIATIONS AA airfi eld approach/early descent system HP high pressure RA runway/fi nal approach AAIB UK Air Accidents EGPWS enhanced ground IFR instrument fl ight rules RNAV area navigation Investigation Branch proximity warning system IMC instrument meteorological SB service bulletin AAL above airfi eld level EGT exhaust gas temperature conditions SID standard instrument departure ADC air-data computer EICAS engine indicating and crew ILS instrument-landing system TAWS terrain awareness and ADF automatic direction fi nder alerting system ISA international standard warning system AF air force ER en route atmosphere = sea level pressure of TO take-off AGL above ground level ETOPS extended-range twin 1013.2mb and standard temp - TOGA press-button selected take- AMSL above mean sea level operations erature/pressure lapse rate off/go-around thrust AOA angle of attack FAA US Federal -

The RAAF Air Board in 1928, with Air Commodore Williams
UNCLASSIFIED This material is compiled from sources including the Office of Air Force History, the RAAF Museum and the Australian War Memorial. The Office of Air Force History is not responsible for pre-1921 items. Whilst every effort is made to confirm the accuracy of the entries, any discrepancies are solely the responsibility of the originator. 2 Oct 22 – Chief of the Air Staff post created The RAAF Air Board in 1928, with Air Commodore Williams (front row, centre) as Chief of the Air Staff, and Group Captain Stanley Goble (front row, left) On this day, the title of the Director of Intelligence and Organisation position at Air Force Headquarters -- held at the time by Wing Commander Richard Williams -- was redesignated as Chief of the Air Staff (CAS) and First Air Member of the Air Board. When the CAS appointment was instituted, the RAAF had less than 350 personnel. The RAAF’s next most senior officer, Wing Commander Stanley Goble, formerly known as Director of Personnel and Training, became Chief of the Administrative Staff and Second Air Member. The idea of making the CAS ‘first among equals’ on the Air Board replicated the arrangements on the Naval and Military Boards of Administration, but was also meant to assuage a bitter personal rivalry developing between Williams and Goble. The change also gave the RAAF a head of service comparable in status to the Army and Navy, although Williams did not reach equivalent rank of his military and naval counterparts until 1935, when he became an Air Vice-Marshal. More on the early days of the RAAF in the Official History here: https://static.awm.gov.au/images/collection/pdf/RCDIG1070474--1-.pdf 2 Oct 52 – RAF exchange pilot killed in action in Korea Flying Officer Oliver Cruickshank, an RAF pilot on exchange with No 77 Squadron flying Meteors in Korea, was killed in action on this day. -

Access the Latest M250 Directory Here
2018 FIRST network M250 Directory Table of Contents Rolls-Royce M250 Support Team .......................................................................................3 Authorized Military Overhaul Facilities (AMOF) ...............................................................41 Rolls‑Royce Aftermarket Services .....................................................................................................4 AMOF.......... ................................................................................................................................................42 Rolls‑Royce First Network ....................................................................................................................5 Air Asia Company, Limited...................................................................................................................43 Rolls‑Royce Customer Services ..........................................................................................................7 HANWHA Techwin Co., Ltd. ................................................................................................................44 Rolls‑Royce Civil Field Support ..........................................................................................................8 Piaggio Aero Industries, S.P.A. ...........................................................................................................45 Rolls‑Royce Regional Customer Training Center ...................................................................... 10 Authorized Repair