Geometric Knowledge of the Indus Civilization
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 Arthur M. Sackler Colloquium of the National Academy Of
1 Arthur M. Sackler Colloquium of the National Academy of Sciences Early Cities: New Perspectives on Pre-Industrial Urbanism Final Revisions: Oct. 1, 2005 Indus Urbanism: New Perspectives on its Origin and Character Jonathan Mark Kenoyer, Department of Anthropology, University of Wisconsin, Madison During the past two decades a variety of archaeological research projects focused on the Indus civilization have made it possible to refine earlier models regarding the origin and character of this distinctive urban society. Excavations at the major city of Harappa have revealed a long developmental sequence from its origins to its eventual decline and subsequent transformation. Recent excavations at the large urban centers of Dholavira and Rakhigarhi, along with reexamination of the largest city of Mohenjo-daro have shown that the development of urbanism was not uniform throughout the greater Indus region (Kenoyer 1998). Detailed studies within each city have revealed many shared characteristics as well as some unique features relating to the dynamic process of city growth and decline. In addition to the excavations of larger urban centers, regional surveys and extensive excavations at smaller settlements have provided a new perspective on the nature of interaction between large and small urban centers and even rural settlements. The increase in radiocarbon dates from well-documented contexts in stratigraphic excavations has helped to refine the chronology of settlements in both core areas and rural areas (Meadow and Kenoyer 2005b; Possehl 2002a; Possehl 2002c). On the basis of a more refined chronology and comparisons of the material culture, it appears that some rural settlements may have been directly linked to the major cities, while others appear to have had relatively little direct contact during some time periods (Meadow and Kenoyer 2005b). -

ICONS and SIGNS from the ANCIENT HARAPPA Amelia Sparavigna ∗ Dipartimento Di Fisica, Politecnico Di Torino C.So Duca Degli Abruzzi 24, Torino, Italy
ICONS AND SIGNS FROM THE ANCIENT HARAPPA Amelia Sparavigna ∗ Dipartimento di Fisica, Politecnico di Torino C.so Duca degli Abruzzi 24, Torino, Italy Abstract Written words probably developed independently at least in three places: Egypt, Mesopotamia and Harappa. In these densely populated areas, signs, icons and symbols were eventually used to create a writing system. It is interesting to see how sometimes remote populations are using the same icons and symbols. Here, we discuss examples and some results obtained by researchers investigating the signs of Harappan civilization. 1. Introduction The debate about where and when the written words were originated is still open. Probably, writing systems developed independently in at least three places, Egypt, Mesopotamia and Harappa. In places where an agricultural civilization flourished, the passage from the use of symbols to a true writing system was early accomplished. It means that, at certain period in some densely populated area, signs and symbols were eventually used to create a writing system, the more complex society requiring an increase in recording and communication media. Signs, symbols and icons were always used by human beings, when they started carving wood or cutting stones and painting caves. We find signs on drums, textiles and pottery, and on the body itself, with tattooing. To figure what symbols used the human population when it was mainly composed by small groups of hunter-gatherers, we could analyse the signs of Native Americans. Our intuition is able to understand many of these old signs, because they immediately represent the shapes of objects and animals. It is then quite natural that signs and icons, born among people in a certain region, turn out to be used by other remote populations. -

3-Art-Of-Indus-Valley.Pdf
Harappan civilization 2 Architecture 2 Drainage System 3 The planning of the residential houses were also meticulous. 4 Town Planning 4 Urban Culture 4 Occupation 5 Export import product of 5 Clothing 5 Important centres 6 Religious beliefs 6 Script 7 Authority and governance 7 Technology 8 Architecture Of Indus Valley Civilisation 9 The GAP 9 ARTS OF THE INDUS VALLEY 11 Stone Statues 12 MALE TORSO 12 Bust of a bearded priest 13 Male Dancer 14 Bronze Casting 14 DANCING GIRL 15 BULL 16 Terracotta 16 MOTHER GODDESS 17 Seals 18 Pashupati Seal 19 Copper tablets 19 Bull Seal 20 Pottery 21 PAINTED EARTHEN JAR 22 Beads and Ornaments 22 Toy Animal with moveable head 24 Page !1 of !26 Harappan civilization India has a continuous history covering a very long period. Evidence of neolithic habitation dating as far back as 7000 BC has been found in Mehrgarh in Baluchistan. However, the first notable civilization flourished in India around 2700 BC in the north western part of the Indian subcontinent, covering a large area. The civilization is referred to as the Harappan civilization. Most of the sites of this civilization developed on the banks of Indus, Ghaggar and its tributaries. Architecture The excavations at Harappa and Mohenjodaro and several other sites of the Indus Valley Civilisation revealed the existence of a very modern urban civilisation with expert town planning and engineering skills. The very advanced drainage system along with well planned roads and houses show that a sophisticated and highly evolved culture existed in India before the coming of the Aryans. -

Indus Valley Civilization
Name: edHelper Indus Valley Civilization A long, long time ago, there was a group of people called the Aryans. The Aryans were possibly from southern Russia and Central Asia. As nomads, they never liked to linger in one place. Instead, they much preferred to herd their animals by moving them from one spot to another. About 3,600 years ago, the Aryans decided to change their lifestyle. They wanted to give up endless wandering. They wanted to have a permanent settlement that they could call home. When they arrived in India, they did exactly that. As the Aryans learned to adapt to their new environment, they brought with them their religion and customs. Their culture later became the foundation of the Indian culture and led people to believe that it was India's oldest civilization. That notion changed completely in 1921! In 1921, archaeologists unearthed two ancient cities - Harappa and Mohenjo-daro - near the Indus River. Both sites predated the Aryans' settlement by about 1,000 years. The discovery, undoubtedly, was a surprise to everybody. Right away, it pushed the Indian history back even further than it already was. Scholars around the world termed the newly found culture "the Indus valley civilization." Some also called it "the Harappan civilization" because Harappa was the first city the archaeologists dug out. The Indus River lies on the western side of the Indian subcontinent. Today, both the river itself and the two ancient cities fall within the confines of Pakistan. The excavations indicated that people of this ancient culture were excellent city planners. -

Arts of the Indus Valley
2 ARTS OF THE INDUS VALLEY HE arts of the Indus Valley Civilisation emerged during Tthe second half of the third millennium BCE. The forms of art found from various sites of the civilisation include sculptures, seals, pottery, jewellery, terracotta figures, etc. The artists of that time surely had fine artistic sensibilities and a vivid imagination. Their delineation of human and animal figures was highly realistic in nature, since the anatomical details included in them were unique, and, in the case of terracotta art, the modelling of animal figures was done in an extremely careful manner. The two major sites of the Indus Valley Civilisation, along the Indus river—the cities of Harappa in the north and Mohenjodaro in the south—showcase one of earliest examples of civic planning. Other markers were houses, markets, storage facilities, offices, public baths, etc., arranged in a grid-like pattern. There was also a highly developed drainage system. While Harappa and Mohenjodaro are situated in Pakistan, the important sites excavated in India are Lothal and Dholavira in Gujarat, Rakhigarhi in Haryana, Bust of a bearded priest Ropar in Punjab, Kalibangan in Rajasthan, etc. Stone Statues Statues whether in stone, bronze or terracotta found in Harappan sites are not abundant, but refined. The stone statuaries found at Harappa and Mohenjodaro are excellent examples of handling three-dimensional volumes. In stone are two male figures—one is a torso in red sandstone and the other is a bust of a bearded man in soapstone—which are extensively discussed. The figure of the bearded man, interpreted as a priest, is draped in a shawl coming under the right arm and covering the left shoulder. -

Languages of Harappa
•§ Michael Witzel Feb. 17, 2000 135 k The Languages of Harappa § 1. The riddle of the Indus script and language Each year, or as it seems, by now every other month, we see a new decipherment of the Indus script. Beyond G. Possehl's fifty-odd examples (Possehl 1996), there must be some dozens more, by now frequently found on the internet. However, as is well known, neither is the script itself well understood nor do we know on which language it is based and for which languages it has been used. In this paper, I am not going to add myself to the long list of failures of decipherment of the script. Instead, I think we should first prepare the ground for such undertaking by investigating the peculiarities of the script itself, a task that has not been carried systematically enough (Wells 1998). Secondly, we should take a much closer look at the various sources which may indicate which languages were spoken in the core areas of the Indus civilization, in the Greater Panjab and in Sindh-Baluchistan. During the past few decades, the language underlying the Indus script has almost universally been taken as Proto-Dravidian (leaving aside such unlikely explanations as Sanskrit, Sumerian, etc., see Possehl 1996). This means a form of reconstructed, early Dravidian that precedes --by some two thousand years or more-- that of the Sangam (Cakam) texts which were composed in archaic Tamil around the beginning of our era. The tacit presupposition has been that the by and large South Indian Dravidian languages preceded the various dialects of Old Indo-Aryan (OIA) in the Panjab and Sindh. -

Dholavira 'Prime-Ratio' of Indus Valley Civilization
Dholavira ‘prime ratio’ of Indus valley civilization In my last blog post, I discussed the “divine ratio” and this time around it is about another amazing ratio - the “Dholavira prime ratio”. It belonged to the ancient Indus valley civilization and was discovered in our own backyard, Dholavira in Kutch, in the state of Gujarat. The Indus valley civilization, which dates back to 4000 BC, was a Bronze Age civilization that thrived in the basins of the river Indus, across Afghanistan, Pakistan and India. Its matured phase, however, flourished during the period circa 2600 to 1900 BC and is revealed in the famous cites of Harappa, Mohenjo-Daro (Pakistan) and in Dholavira, Lothal and Juni Kuran in India. Dholavira ‘prime ratio’ The ancient site at Dholavira lies in the island of Khadir in Bhachau, Kutch, in Gujarat. The island is one of the three prominent landmarks, the Bela, Khadir and Paccham bet islands, surrounded by the salt waste of the Great Rann of Kutch and known for their unique geologic significance. Incidentally, I led the ONGC gravity-magnetic survey party to Kutch, in 1962, which camped in Bachau. As an observer, I did a ‘parikrama’ of the site by moving around the three islands, recording gravity and magnetic data, but had no inkling then of the great buried site, till Dholavira was discovered in 1967-68 and excavated in 1990, unraveling the marvels of the amazing civilization. Dholavira city is unique with the buildings built of stone, whereas most other Indus civilization sites including Harappa and Mohenjo-Daro cities are almost exclusively built of brick. -

Indus Valley Civilization: Enigmatic, Exemplary, and Undeciphered Charise Joy Javonillo College of Dupage
ESSAI Volume 8 Article 21 4-1-2011 Indus Valley Civilization: Enigmatic, Exemplary, and Undeciphered Charise Joy Javonillo College of DuPage Follow this and additional works at: http://dc.cod.edu/essai Recommended Citation Javonillo, Charise Joy (2010) "Indus Valley Civilization: Enigmatic, Exemplary, and Undeciphered," ESSAI: Vol. 8, Article 21. Available at: http://dc.cod.edu/essai/vol8/iss1/21 This Selection is brought to you for free and open access by the College Publications at [email protected].. It has been accepted for inclusion in ESSAI by an authorized administrator of [email protected].. For more information, please contact [email protected]. Javonillo: Indus Valley Civilization Indus Valley Civilization: Enigmatic, Exemplary, and Undeciphered by Charise Joy Javonillo (Anthropology 1120) Introduction mong the four great ancient civilizations of the Old World, the Indus Valley Civilization (IVC) has the distinction of being the most enigmatic of this notable group (Kenoyer and AMeadow, 2000). Mindful of the inevitable comparisons to its better represented, recorded, and studied Western contemporaries Mesopotamia and Egypt, four major comparable aspects of the Indus Valley will be presented and discussed in this review. Beginning with settlement patterns, special attention is paid to Harappa and Mohenjo-Daro and specifically to the urban layout of these two exemplary cities. Second is the Indus’ sphere of influence as suggested by possible interaction with Mesopotamia, including motifs found in artwork and seals. Next is a synthesis and discussion about the current debate over the Indus Valley script and its decipherment. Lastly, possible theories are reviewed regarding the collapse and disappearance of the IVC. -

The Decline of Harappan Civilization K.N.DIKSHIT
The Decline of Harappan Civilization K.N.DIKSHIT EBSTRACT As pointed out by N. G. Majumdar in 1934, a late phase of lndus civilization is illustrated by pottery discovered at the upper levels of Jhukar and Mohenjo-daro. However, it was the excavation at Rangpur which revealed in stratification a general decline in the prosperity of the Harappan culture. The cultural gamut of the nuclear region of the lndus-Sarasvati divide, when compared internally, revealed regional variations conforming to devolutionary tendencies especially in the peripheral region of north and western lndia. A large number of sites, now loosely termed as 'Late Harappan/Post-urban', have been discovered. These sites, which formed the disrupted terminal phases of the culture, lost their status as Harappan. They no doubt yielded distinctive Harappan pottery, antiquities and remnants of some architectural forms, but neither town planning nor any economic and cultural nucleus. The script also disappeared. ln this paper, an attempt is made with the survey of some of these excavated sites and other exploratory field-data noticed in the lndo-Pak subcontinent, to understand the complex issue.of Harappan decline and its legacy. CONTENTS l.INTRODUCTION 2. FIELD DATA A. Punjab i. Ropar ii. Bara iii. Dher Majra iv. Sanghol v. Katpalon vi. Nagar vii. Dadheri viii. Rohira B. Jammu and Kashmir i. Manda C. Haryana i. Mitathal ii. Daulatpur iii. Bhagwanpura iv. Mirzapur v. Karsola vi. Muhammad Nagar D. Delhi i. Bhorgarh 125 ANCiENT INDlA,NEW SERIES,NO.1 E.Western Uttar Pradesh i.Hulas il.Alamgirpur ili.Bargaon iv.Mandi v Arnbkheri v:.Bahadarabad F.Guiarat i.Rangpur †|.Desalpur ili.Dhola宙 ra iv Kanmer v.」 uni Kuran vi.Ratanpura G.Maharashtra i.Daimabad 3.EV:DENCE OF RICE 4.BURIAL PRACTiCES 5.DiSCUSS10N 6.CLASSiFiCAT10N AND CHRONOLOGY 7.DATA FROM PAKISTAN 8.BACTRIA―MARGIANAARCHAEOLOGICAL COMPLEX AND LATE HARAPPANS 9.THE LEGACY 10.CONCLUS10N ・ I. -
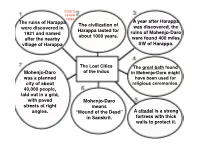
The Ruins of Harappa Were Discovered in 1921 and Named After The
Click to reveal notes The ruins of Harappa A year after Harappa The civilization of were discovered in was discovered, the Harappa lasted for 1921 and named ruins of Mohenjo-Daro about 1000 years. after the nearby were found 400 miles village of Harappa SW of Harappa. The Lost Cities The great bath found Mohenjo-Daro of the Indus in Mohenjo-Daro might was a planned have been used for city of about religious ceremonies. 40,000 people, laid out in a grid, with paved Mohenjo-Daro streets at right means angles. “Mound of the Dead” A citadel is a strong in Sanskrit. fortress with thick walls to protect it. Almost identical Planned Cities-- Harappan cities layouts of Harappa Standard had sewer and Mohenjo-Daro measurements were systems, and indicate that there was used to make bricks many homes had probably a strong that were all the same toilets. central government size. that planned the cities. Harappan Culture Trade routes (Khyber Conclusions about Harappan culture are Pass) connected the Indus Specialized skills-- based on artifacts and Valley and Mesopotamia. Ancient Harappans remains of Mohenjo-Daro. Indus Valley traders traded were skilled engineers ivory, copper, and beads and craftworkers, for cloth, oil, and barley. making elegant jewelry, beautiful Harappans grew new seals, and decorated crops, like cotton, pottery, as well as mustard, and black Surplus food copper fish pepper, as well as wheat, allowed for the hooks. bananas, barley, and specialization of sesame jobs. Cities of the Indus About 1500 BC, a Valley were abandoned group of people from about 1600 BC, Asia, called the Aryans, Aryans means possibly because of crossed the Hindu- “noble ones” in earthquake, drought, Kush mountains into Sanskrit. -

9 Everyday Life in Mohenjo-Daro and Harappa
9 EVERYDAY LIFE IN MOHENJO-DARO AND HARAPPA A highly developed civilization flourished in the Indus Valley about 1,000 years, first appearing around 2S00 B.C. This early civilization developed at the site of the ancient cities of Mohenjo-Daro and Harappa. The excerpt below from The World of the Past, edited by Jacquetta Hopkins Hawkes, draws on archaeological findings in the twin cities to build a picture of everyday life in the Indus civilization. As you read the excerpt, compare life in the Indus civilization from life in other civilizations of the same time period. Statue from the cicy ofM flhenjo-Daro he loliowing picture of the life that was led by the Indus peoples ... is Tdrawn by Sir John Marshall... "Like the rest of Western Asia, the Indus Country is still m . .. that age in which arms and utensils of stone continue to be used side by side with those of copper or bronze. Their society is organized in cities; their wealth derived mainly from agricul• ture and trade, which appears to have extended far and wide in all directions, They cultivate wheat and barley as well as the date-palm. They have domesticated the humped zebu [ox], buffalo, and short horned bull, besides the sheep, pig, dog, elephant, and camel; but the cat and probably the horse are unknown to them. For transport they have wheeled vehicles, to which oxen doubtless were yoked. They are skilful metal workers, with a plentiful supply of gold, silver, and copper. Lead, too, and. tie are in use, but the latter only as an alloy in the making 16 READINGS !M WORLD HISTORY "of bronze. -

States and Social Complexity: the Indus Valley (Harappan) Civilisation
States and Social Complexity 9 States and Social Complexity: the Indus Valley (Harappan) Civilisation Thomas Riisfeldt First year Undergraduate, University of New South Wales The three earliest civilisations, in Mesopotamia, Egypt and the Indus Valley, arose and existed independently around three-thousand B.C.E.1 This essay argues that the Indus Valley Civilisation was organised in a politically dissimilar way to the contemporary Mesopotamian and Egyptian Civilisations, despite being of comparable social complexity. Although decipherable written records and convincing archaeological evidence from Mesopotamia and Egypt substantiates these Civilisations’ classifications as ‘states,’ the same cannot be said for Indus Valley Civilisation. Indus Valley Civilisation was not a state, demonstrated through the Civilisation’s apparent lack of an upper administrative class, state religion and monopoly of force.2 This argument is important for all historians to consider, including those unfamiliar with the Indus Valley, two reasons. Firstly, it examines an instance of poor historiographical method, whereby Indus Valley Civilisation was assumed to be a state like Mesopotamia and Egypt despite a paucity of evidence supporting this assumption. Secondly, it explores the origin and functions of the ‘state’ by challenging the ‘unilineal’ interrelation between social complexity and statehood. This essay ultimately argues, through the inability of this paradigm to accommodate Indus Valley Civilisation, that the state is not the only political form capable