Enhancement and Suppression of Four-Wave Mixing in a Four-Level Atomic System *
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

View / Download 7.3 Mb
Between Shanghai and Mecca: Diaspora and Diplomacy of Chinese Muslims in the Twentieth Century by Janice Hyeju Jeong Department of History Duke University Date:_______________________ Approved: ___________________________ Engseng Ho, Advisor ___________________________ Prasenjit Duara, Advisor ___________________________ Nicole Barnes ___________________________ Adam Mestyan ___________________________ Cemil Aydin Dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Department of History in the Graduate School of Duke University 2019 ABSTRACT Between Shanghai and Mecca: Diaspora and Diplomacy of Chinese Muslims in the Twentieth Century by Janice Hyeju Jeong Department of History Duke University Date:_______________________ Approved: ___________________________ Engseng Ho, Advisor ___________________________ Prasenjit Duara, Advisor ___________________________ Nicole Barnes ___________________________ Adam Mestyan ___________________________ Cemil Aydin An abstract of a dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy, in the Department of History in the Graduate School of Duke University 2019 Copyright by Janice Hyeju Jeong 2019 Abstract While China’s recent Belt and the Road Initiative and its expansion across Eurasia is garnering public and scholarly attention, this dissertation recasts the space of Eurasia as one connected through historic Islamic networks between Mecca and China. Specifically, I show that eruptions of -

China Turns up Heat on Ex-Security Chief with Crash Probe
CHINA PRIME TARGET: Zhou Yongkang was head of domestic security and a member of the Communist Party Standing Politburo Committee, making him one of the most powerful people in China, until he stepped down in 2012. REUTERS/STRINGER Authorities have begun investigating a crash in 2000 that killed the first wife of Zhou Yongkang, the prime target in China’s biggest corruption scandal, Reuters source says. China turns up heat on ex-security chief with crash probe BY BENJAMIN KANG LIM, CHARLIE ZHU AND DAVID LAGUE SPECIAL REPORT 1 CHINA’S POWER STRUGGLE BEIJING/HONG KONG, SEPTEMBER 12, 2014 ittle is known about the exact circum- stances in which Wang Shuhua was Lkilled. What has been reported, in the Chinese media, is that she died in a road ac- cident sometime in 2000, shortly after she was divorced from her husband. And that at least one vehicle with a military license plate may have been involved in the crash. Fourteen years later, investigators are looking into her death. Their sudden inter- est has nothing to do with Wang herself. It has to do with the identity of her ex-hus- band – once one of China’s most powerful men and now the prime target in President Xi Jinping’s anti-corruption campaign. Investigators are probing the death of the first wife of Zhou Yongkang, China’s HUNTING TIGERS: President Xi Jinping has launched the biggest corruption crackdown since the retired security czar, a source with di- communists came to power in 1949, going after “tigers” or high-ranking officials as well as “flies”. -

The Lions's Share, Act 2. What's Behind China's Anti-Corruption Campaign?
The Lions’s Share, Act 2. What’s Behind China’s Anti-Corruption Campaign? Guilhem Fabre To cite this version: Guilhem Fabre. The Lions’s Share, Act 2. What’s Behind China’s Anti-Corruption Campaign?. 2015. halshs-01143800 HAL Id: halshs-01143800 https://halshs.archives-ouvertes.fr/halshs-01143800 Preprint submitted on 20 Apr 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Séminaire BRICs FMSH - CRBC The Lions’s Share, Act 2. What’s Behind China’s Anti-Corruption Campaign? Guilhem Fabre N°92 | april 2015 As we have seen in a previous working paper ( « The lion’s share : What’s behind China’s economic slowdown ? »), China’s elite have largely benefited from control of state assets and manipulation of the factors market (land, labor and capital) during the first decade of this cen- tury. Along with strong growth and social mobility, the accumulation of wealth has created some of the most flagrant social polarization worldwide, much higher than the official statistics. Instead of taking concrete measures to correct these inequalities, according to the new blueprint of reforms launched by the 3rd Plenum in November 2013, the new direction has focused on a gigantic campaign against corruption. -

P020110307527551165137.Pdf
CONTENT 1.MESSAGE FROM DIRECTOR …………………………………………………………………………………………………………………………………………………… 03 2.ORGANIZATION STRUCTURE …………………………………………………………………………………………………………………………………………………… 05 3.HIGHLIGHTS OF ACHIEVEMENTS …………………………………………………………………………………………………………………………………………… 06 Coexistence of Conserve and Research----“The Germplasm Bank of Wild Species ” services biodiversity protection and socio-economic development ………………………………………………………………………………………………………………………………………………… 06 The Structure, Activity and New Drug Pre-Clinical Research of Monoterpene Indole Alkaloids ………………………………………… 09 Anti-Cancer Constituents in the Herb Medicine-Shengma (Cimicifuga L) ……………………………………………………………………………… 10 Floristic Study on the Seed Plants of Yaoshan Mountain in Northeast Yunnan …………………………………………………………………… 11 Higher Fungi Resources and Chemical Composition in Alpine and Sub-alpine Regions in Southwest China ……………………… 12 Research Progress on Natural Tobacco Mosaic Virus (TMV) Inhibitors…………………………………………………………………………………… 13 Predicting Global Change through Reconstruction Research of Paleoclimate………………………………………………………………………… 14 Chemical Composition of a traditional Chinese medicine-Swertia mileensis……………………………………………………………………………… 15 Mountain Ecosystem Research has Made New Progress ………………………………………………………………………………………………………… 16 Plant Cyclic Peptide has Made Important Progress ………………………………………………………………………………………………………………… 17 Progresses in Computational Chemistry Research ………………………………………………………………………………………………………………… 18 New Progress in the Total Synthesis of Natural Products ……………………………………………………………………………………………………… -

Journal of Current Chinese Affairs
China Data Supplement May 2007 J People’s Republic of China J Hong Kong SAR J Macau SAR J Taiwan ISSN 0943-7533 China aktuell Data Supplement – PRC, Hong Kong SAR, Macau SAR, Taiwan 1 Contents The Main National Leadership of the PRC .......................................................................... 2 LIU Jen-Kai The Main Provincial Leadership of the PRC ..................................................................... 30 LIU Jen-Kai Data on Changes in PRC Main Leadership ...................................................................... 37 LIU Jen-Kai PRC Agreements with Foreign Countries ......................................................................... 42 LIU Jen-Kai PRC Laws and Regulations .............................................................................................. 44 LIU Jen-Kai Hong Kong SAR ................................................................................................................ 45 LIU Jen-Kai Macau SAR ....................................................................................................................... 52 LIU Jen-Kai Taiwan .............................................................................................................................. 56 LIU Jen-Kai ISSN 0943-7533 All information given here is derived from generally accessible sources. Publisher/Distributor: GIGA Institute of Asian Studies Rothenbaumchaussee 32 20148 Hamburg Germany Phone: +49 (0 40) 42 88 74-0 Fax: +49 (040) 4107945 2 May 2007 The Main National Leadership of the PRC -
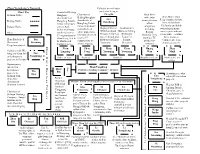
Zhou Yongkang's Network
Zhou Yongkang’s Network Colluded on real estate Chart Key Controlled Beijing project w/ Feng in Sichuan Native Honghan; Chairman of Chengdu Zhou Bin’s Zhan Minli, Zhou shareholder of Beijing Honghan; wife, who Sun Feng’s mother-in-law, Beijing Native Hongfeng Potash shareholder of managed many Jiancheng lives in Southern mines in Sichuan, Hongfeng Potash of his California and holds Jiangsu Native owned Audi mines in Sichuan; companies, ` Deputy Chief of Established A dealer in Jiangsu; controlled real including ownership in many— Wuxi Land and Business Selling Other involved in over estate projects in Beijing some reports indicate Resources Bureau; Wuliangye at least nine—of Zhou 37 corporations w/ Chengdu involved Zhongxu; Also travelled back and Liquor in Bin’s business Zhou Feng; tied to in over 37 started a TV Zhou Bin helped Dai forth to visit Zhou Jiangsu; ventures; she is an Li Hualin and corporations w/ production Dai secure Xiaoming Yonakang Deceased American citizen Kunlun Energy Zhou Lingying company Pengzhou project Zhou Bin’s Business Partners Business Bin’s Zhou Zhou Zhou Zhou Zhou Huang Zhan Colluded with Wu Lingying Feng Yuanqing Yuanxing Wan Minli Guo Bing and Zhou Bin Yongxiang on hydropower Sister-in-Law Nephew Brothers Daughter-in-Law Mother-in-Law projects in Sichuan of Son Businessman, invested in Son Zhou Yongkang hydropower Zhou Politburo Standing Committee Member Wu Bin projects in Bing A soothsayer, who Cao Sichuan with advised Li on urban Zhou Bin; Former Yongzheng projects; chairman of Chairman Major Zhou Surrogates/Secretaries in Sichuan Zhongxu Limited of Beijing Head of PSB in Zhongxu Guo Li Li Wu Jinjiang District, Yangguang Yongxiang Chongxi Chuncheng Tao Chengdu, gave Li Chairman of Petroleum Sichuan Hanlong illegal passports Liu and Natural Former Vice- Former Deputy Mayor of Chengdu; Company. -

A Visualization Quality Evaluation Method for Multiple Sequence Alignments
2011 5th International Conference on Bioinformatics and Biomedical Engineering (iCBBE 2011) Wuhan, China 10 - 12 May 2011 Pages 1 - 867 IEEE Catalog Number: CFP1129C-PRT ISBN: 978-1-4244-5088-6 1/7 TABLE OF CONTENTS ALGORITHMS, MODELS, SOFTWARE AND TOOLS IN BIOINFORMATICS: A Visualization Quality Evaluation Method for Multiple Sequence Alignments ............................................................1 Hongbin Lee, Bo Wang, Xiaoming Wu, Yonggang Liu, Wei Gao, Huili Li, Xu Wang, Feng He A New Promoter Recognition Method Based On Features Optimal Selection.................................................................5 Lan Tao, Huakui Chen, Yanmeng Xu, Zexuan Zhu A Center Closeness Algorithm For The Analyses Of Gene Expression Data ...................................................................9 Huakun Wang, Lixin Feng, Zhou Ying, Zhang Xu, Zhenzhen Wang A Novel Method For Lysine Acetylation Sites Prediction ................................................................................................ 11 Yongchun Gao, Wei Chen Weighted Maximum Margin Criterion Method: Application To Proteomic Peptide Profile ....................................... 15 Xiao Li Yang, Qiong He, Si Ya Yang, Li Liu Ectopic Expression Of Tim-3 Induces Tumor-Specific Antitumor Immunity................................................................ 19 Osama A. O. Elhag, Xiaojing Hu, Weiying Zhang, Li Xiong, Yongze Yuan, Lingfeng Deng, Deli Liu, Yingle Liu, Hui Geng Small-World Network Properties Of Protein Complexes: Node Centrality And Community Structure -

Final Program of CCC2020
第三十九届中国控制会议 The 39th Chinese Control Conference 程序册 Final Program 主办单位 中国自动化学会控制理论专业委员会 中国自动化学会 中国系统工程学会 承办单位 东北大学 CCC2020 Sponsoring Organizations Technical Committee on Control Theory, Chinese Association of Automation Chinese Association of Automation Systems Engineering Society of China Northeastern University, China 2020 年 7 月 27-29 日,中国·沈阳 July 27-29, 2020, Shenyang, China Proceedings of CCC2020 IEEE Catalog Number: CFP2040A -USB ISBN: 978-988-15639-9-6 CCC2020 Copyright and Reprint Permission: This material is permitted for personal use. For any other copying, reprint, republication or redistribution permission, please contact TCCT Secretariat, No. 55 Zhongguancun East Road, Beijing 100190, P. R. China. All rights reserved. Copyright@2020 by TCCT. 目录 (Contents) 目录 (Contents) ................................................................................................................................................... i 欢迎辞 (Welcome Address) ................................................................................................................................1 组织机构 (Conference Committees) ...................................................................................................................4 重要信息 (Important Information) ....................................................................................................................11 口头报告与张贴报告要求 (Instruction for Oral and Poster Presentations) .....................................................12 大会报告 (Plenary Lectures).............................................................................................................................14 -

The Neolithic Ofsouthern China-Origin, Development, and Dispersal
The Neolithic ofSouthern China-Origin, Development, and Dispersal ZHANG CHI AND HSIAO-CHUN HUNG INTRODUCTION SANDWICHED BETWEEN THE YELLOW RIVER and Mainland Southeast Asia, southern China1 lies centrally within eastern Asia. This geographical area can be divided into three geomorphological terrains: the middle and lower Yangtze allu vial plain, the Lingnan (southern Nanling Mountains)-Fujian region,2 and the Yungui Plateau3 (Fig. 1). During the past 30 years, abundant archaeological dis coveries have stimulated a rethinking of the role ofsouthern China in the prehis tory of China and Southeast Asia. This article aims to outline briefly the Neolithic cultural developments in the middle and lower Yangtze alluvial plain, to discuss cultural influences over adjacent regions and, most importantly, to examine the issue of southward population dispersal during this time period. First, we give an overview of some significant prehistoric discoveries in south ern China. With the discovery of Hemudu in the mid-1970s as the divide, the history of archaeology in this region can be divided into two phases. The first phase (c. 1920s-1970s) involved extensive discovery, when archaeologists un earthed Pleistocene human remains at Yuanmou, Ziyang, Liujiang, Maba, and Changyang, and Palaeolithic industries in many caves. The major Neolithic cul tures, including Daxi, Qujialing, Shijiahe, Majiabang, Songze, Liangzhu, and Beiyinyangying in the middle and lower Yangtze, and several shell midden sites in Lingnan, were also discovered in this phase. During the systematic research phase (1970s to the present), ongoing major ex cavation at many sites contributed significantly to our understanding of prehis toric southern China. Additional early human remains at Wushan, Jianshi, Yun xian, Nanjing, and Hexian were recovered together with Palaeolithic assemblages from Yuanmou, the Baise basin, Jianshi Longgu cave, Hanzhong, the Li and Yuan valleys, Dadong and Jigongshan. -

SUMMER / 2013 Wang Anyi Yi Sha Bai Hua Bi Feiyu Li Hao Zang Di Jiang Yun Lu Nei Yang Li Speed Photo by Qiu Lei
PATHLIGHT NEW CHINESE WRITING SUMMER / 2013 Wang Anyi Yi Sha Bai Hua Bi Feiyu Li Hao Zang Di Jiang Yun Lu Nei Yang Li Speed Photo by Qiu Lei PATHLIGHT / SUMMER - 2013 1 Photo by Wang Yan PATHLIGHT SUMMER / 2013 Summer 2013 ISBN 978-7-119-08377-3 © Foreign Languages Press Co. Ltd, Beijing, China, 2013 Published by Foreign Languages Press Co. Ltd. 24 Baiwanzhuang Road, Beijing 100037, China http://www.flp.com.cn E-mail: [email protected] Distributed by China International Book Trading Corporation 35 Chegongzhuang Xilu, Beijing 100044, China P.O. Box 399, Beijing, China Printed in the People’s Republic of China CONTENTS Fiction 004 Wang Anyi _ In the Belly of the Fog _ 4 Tradition and Rebellion: A Conversation with Wang Anyi _ 12 Bi Feiyu _ The Deluge _ 18 A Professional Interest in Suffering: A Conversation with Bi Feiyu _ 36 Jiang Yun _ The Red Detachment of Women _ 46 Li Hao _ The General _ 58 Lu Nei _ Keep Running, Little Brother _ 66 A Yi _ Two Lives _ 88 Ren Xiaowen _ I Am Fish _ 100 Su Cici _ The Zebra That Didn’t Exist _ 110 Sheng Tie _ The Train Was Clean and Cool _ 122 Poetry 132 Bai Hua _ Small Town Tale, Village, 1977, Mock Nursery Rhyme, The Illusion of Life, Thoughts Arising from the Pig _ 132 Yang Li _ Fated, An Old Poem, The White Horse, Courthouse (I) _ 138 Yi Sha _ Rhythm is What Matters, Memories Evoked by Reality, Notes on Mt. -

Self-Consistent Approach for Mapping Interacting Systems in Continuous
ISSN: 0256-307X 中国物理快报 Chinese Physics Letters Volume 29 Number 8 August 2012 A Series Journal of the Chinese Physical Society Distributed by IOP Publishing Online: http://iopscience.iop.org/cpl http://cpl.iphy.ac.cn C HINESE P HYSICAL S OCIETY CHIN. PHYS. LETT. Vol. 29, No. 8 (2012) 083701 Self-Consistent Approach for Mapping Interacting Systems in Continuous Space to Lattice Models * WU Biao(Ç飙)1**, XU Yong(M])2, DONG Lin(Â霖)3, SHI Jun-Ren(施均;)1 1International Center for Quantum Materials, Peking University, Beijing 100871 2Institute of Physics, Chinese Academy of Sciences, Beijing 100190 3Department of Physics and Astronomy, and Rice Quantum Institute, Rice University, Houston, Texas 77251-1892, USA (Received 23 February 2012) We propose a general variational principle for mapping the interacting systems in continuous space to lattice models. Based on the principle, we derive a set of self-consistent nonlinear equations for the Wannier functions (or, equivalently for the Bloch functions). These equations show that the Wannier functions can be strongly influenced by the interaction and be significantly different from their non-interacting counterparts. Theapproach is demonstrated with interacting bosons in an optical lattice, and illustrated quantitatively by a simple model of interacting bosons in a double well potential. It is shown that the so-determined lattice model parameters can be significantly different from their non-interacting values. PACS: 37.10.Jk, 71.10.Fd DOI: 10.1088/0256-307X/29/8/083701 Although the real condensed matter systems al- linear equations for the Wannier functions (or, equiv- ways live in the continuous space, it is not uncom- alently, the corresponding Bloch functions), with the mon to use lattice models to describe them, for ex- coefficients of the equations expressed in the correla- ample, many systems can be well described by the tion functions of the lattice model. -

XUN XU's FIRST POSTS, CA. 248–265 We Know Next to Nothing
CHAPTER TWO XUN XU’S FIRST POSTS, CA. 248–265 Shang 商: The Harmonious Step Moving away from gong is made comfortable by the harmonious and harmonic shang note. In modes and melodies, shang forms unoffending chords; it cooperates with other notes, like zhi and yu. Harmonics masters knew that the circle-of-fifths derivation, based on gong as “9,” resulted in the pleasing whole number “8” for shang. Xun Xu began his career under the Jin by fitting in with the new regime and cooperat- ing in court projects. We know next to nothing about Xun Xu’s childhood and youth. But from the previous chapter we do know that his family was used to power—power that had first been local, then on the move defensively, next serving Cao Cao’s court at Xu, and finally the Simas in Luoyang. The Xuns offered important political service to the Cao-Wei dynasty, even if the fate of Xun Yu at the hands of Cao Cao had weakened Xun loyalties to that family. Cao Cao’s heirs began to rebuild Luoyang pal- aces and state offices in the 220s, so by the mid-230s such Xun men as Xun Can and Xun Yi began residing there, and the young orphan Xun Xu relied on them, as well as on in-laws, for political grooming and entree. His biography states: Xun Xu was styled Gongceng 公曾. He was a Yingchuan 穎川, Yingyin 穎陰, man, and the great-grandson of Xun Shuang 爽, an [Eastern Han- dynasty] Minister of Works. His grandfather was Xun Fei 棐, who was a Colonel of Archers Who Shoot by Sound.