Tony Skyrme and the Origins of Skyrmions† Ian J. R
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

01 Freer.Pdf
John Henry Poynting First Prof Physics Birmingham 1880-1914 Rudolf Peierls 1907-1995 Birmingham 1937+ (holes in semiconductors) Marcus Laurence Elwin Oliphant 1901-2000 Birmingham 1937-1950 Otto Frisch (1904-1979) Bham 1939+ co-discover of 2H, 3H and 3He Role in first demonstration of nuclear fusion Got plans from Lawrence for Birmingham’s cyclotron John Bell 1928-1990 CPT 1951 Birmingham Luders-Pauli Thm Freeman-Dyson Tony Skyrme (1922-1987) Birmingham, 1949-51 Why are light nuclei so important – Understanding cutting edge theory ? [Otsuka et al., PRL 95 (05) 232502] Tensor correlations [Otsuka et al., PRL 97 (06) 162501] Neutron – proton interaction - - - + + + + - 8Be Ab initio type approaches (Greens Function Monte Carlo) 13 11 + 9 4 7 Ex [MeV] [MeV] Ex Ex 5 3 2+ 1 + -1 0 -1 4 9 14 19 24 Pieper and J(J+1) Wiringa, ANL 9 Ab initio no-core solutions for nuclear structure: Be P. Maris, C. Cockrell, M. Caprio and J.P. Vary Total density Proton - Neutron density Shows that one neutron provides a “ring ” cloud around two alpha clusters binding them together Chase Cockrell, ISU PhD student 12 C Chiral EFT on the lattice 32 S 24 Mg 9Be 9B PHYSICAL REVIEW C 86 , 057306 (2012), PHYSICAL REVIEW C 86 , 014312 (2012) 10 Be 12 C 10 C Characterization of 10 Be * Gas inlet LAMP array Window (2.5 um mylar) LAMP 6He LEDA LAMP LEDA Collimator M. Freer, et al. PRL 2006 Test of method- measure 10.36 MeV 4 + resonance In 16 O ( 12 C+ α) LAMP LEDA LAMP LEDA Resonances in 16 O E( 12 C)=16 MeV Singles Coincidence 10 10 4He Energy Energy (MeV) (MeV) 12 C 0 0 8 24 8 24 Angle Angle Gas pressure = 100 Torr LAMP LEDA LAMP 4 Energy ( 12 C) LEDA θcm ( He) 180 0 Energy ( 4He) 12 180 θcm ( C) Resonance analysis Counts 6000 - =121 mm detector 2000 - (E, θw) ddet window Distance/2+20 (mm) θw θlab dreaction 2 |P 4(cos( θcm )| θcm 6He+ 4He at 7.5 MeV – 7Li+ 7Li the 10.15 MeV state in 10 Be N. -

The Skyrme Model Fundamentals Methods Applications
springer.com Physics : Elementary Particles, Quantum Field Theory Makhankov, V.G., Rybakov, Y.P., Sanyuk, V.I. The Skyrme Model Fundamentals Methods Applications The December 1988 issue of the International Journal of Modern Physics A is dedicated to the memory of Tony Hilton Royle Skyrme. It contains an informative account of his life by Dalitz and Aitchison's reconstruction of a talk by Skyrme on the origin of the Skyrme model. From these pages, we learn that Tony Skyrme was born in England in December 1922. He grew up in that country during a period of increasing economic and political turbulence in Europe and elsewhere. In 1943, after Cambridge, he joined the British war effort in making the atomic bomb. He was associated with military projects throughout the war years and began his career as an academic theoretical physicist only in 1946. During 1946-61, he was associated with Cambridge, Birmingham and Harwell and was engaged in wide-ranging investigations in nuclear physics. It was this research which eventually culminated in his studies of nonlinear field theories and his remarkable proposals for the description of the nucleon as a chiral soliton. In his talk, Skyrme described the reasons behind his extraordinary sug• gestions, which Springer when first made must have seemed bizarre. According to him, ideas of this sort go back many Softcover reprint of the decades and occur in the work of Sir William Thomson, who later became Lord Kelvin. Skyrme 1st original 1st ed. 1993, XVIII, edition had heard of Kelvin in his youth. 265 p. Order online at springer.com/booksellers Springer Nature Customer Service Center LLC Printed book 233 Spring Street Softcover New York, NY 10013 Printed book USA Softcover T: +1-800-SPRINGER NATURE ISBN 978-3-642-84672-4 (777-4643) or 212-460-1500 [email protected] $ 109,99 Available Discount group Professional Books (2) Product category Monograph Series Springer Series in Nuclear and Particle Physics Other renditions Softcover ISBN 978-3-642-84671-7 Prices and other details are subject to change without notice. -

Topology in Physics-A Perspective
SU-4228-533 March 1993 TOPOLOGY IN PHYSICS - A PERSPECTIVE A.P. Balachandran Department of Physics, Syracuse University, Syracuse, NY 13244-1130 ABSTRACT This article, written in honour of Fritz Rohrlich, briefly surveys the role of topology in physics. arXiv:hep-th/9303177v1 31 Mar 1993 When I joined Syracuse University as a junior faculty member in September, 1964, Fritz Rohrlich was already there as a senior theoretician in the quantum field theory group. He was a very well-known physicist by that time, having made fundamental contributions to quantum field theory, and written his splendid book with Jauch. My generation of physicists grew up with Jauch and Rohrlich, and I was also familiar with Fritz’s research. It was therefore with a certain awe and a great deal of respect that I first made his acquaintance. Many years have passed since this first encounter. Our interests too have gradually evolved and changed in this intervening time. Starting from the late seventies or there- abouts, particle physicists have witnessed an increasing intrusion of topological ideas into their discipline. Our group at Syracuse has responded to this development by getting involved in soliton and monopole physics and in investigations on the role of topology in quantum physics. Meanwhile, especially during the last decade, there has been a per- ceptible shift in the direction of Fritz’s research to foundations and history of quantum physics. Later I will argue that topology affects the nature of wave functions (or more accurately of wave functions in the domains of observables) and has a profound meaning for the fundamentals of quantum theory. -
Quark•Gluon Plasma
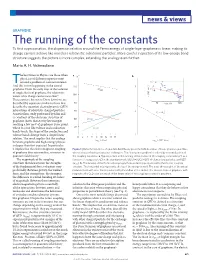
news & views GRAPHENE The running of the constants To first approximation, the dispersion relation around the Fermi energy of single-layer graphene is linear, making its charge carriers behave like massless relativistic subatomic particles. More careful inspection of its low-energy band structure suggests the picture is more complex, extending the analogy even further. Maria A. H. Vozmediano he best times in Physics are those when a α–1 b physicists of different expertise meet around a problem of common interest. 3 T ) And this is now happening in the case of 120 3 –1 α–1 2 graphene. From the early days of the isolation QED ms of single sheets of graphene, the relativistic 6 100 (10 1 F nature of its charge carriers was clear . v These carriers, known as Dirac fermions, are 1 described by equations similar to those that 80 10 E (meV) 100 describe the quantum electrodynamic (QED) interactions of relativistic charged particles. 60 2 U(1) ѵ ~ α–1 A meticulous study performed by Elias and F G 2 co-workers of the electronic structure of 40 SU(2) graphene shows that at very low energies reaching a few meV of graphene’s Dirac point, 20 where its cone-like valence and conduction SU(3) bands touch, the shape of the conduction and valence bands diverge from a simple linear 1 0 2 4 6 8 10 12 14 16 1 2 relation. The result implies that the analogy log E (Gev) log E (10–12 Gev) between graphene and high-energy physics 10 10 is deeper than first expected. -

Bertlmann – a Nonlocal Quantum Engineer
a nonlocal quantum engineer contemplate but don’t forget to calculate ! Reinhold A. Bertlmann Faculty of Physics, University of Vienna talk at symposium “ shut up and contemplate ! ” University of Vienna, March 3rd, 2017 engineer’s career at Harwell John Stewart Bell graduated at Queen’s University Belfast in experimental physics 1948 in mathematical physics 1949 high interest in quantum mechanics showing his dissatisfaction ! position at AERE Harwell from1949 on joined accelerator group of Walkinshaw (Malvern) William Walkinshaw: John on his new “Ariel” “ a young man of high caliber who showed his at Harwell 1952 independence … his mathematical talent was superb and elegant.” papers on electron and proton linear accelerators e.g. “basic algebra on strong focussing systems” “linear accelerator phase oscillations” “phase debunching by focussing foils in proton linear accelerator” Reinhold A. Bertlmann 2 turn to particle physics & Bohm’s qm in mid1950s Bell turned to nuclear and particle physics “time reversal in field theory …”, CPT theorem, PhD thesis fundamental ! “anomalous magnetic moments of nucleons”, collab. Tony Skyrme at that time paper of David Bohm appeared 1952 “interpretation of quantum theory in terms of hidden variable” Mary: for John a “revelation” “everything has definite properties” I remember John saying Bell’s talk about Bohm’s theory in TH division fierce debates with audience especially with Franz Mandl 1954 John married Mary Ross “mathematical engineer” accelerator physicist Reinhold A. Bertlmann 3 engineer’s job -

Aspects of the Many-Body Problem in Nuclear Physics
Aspects of the Many-Body Problem in Nuclear Physics DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Alexander Signatur Dyhdalo, MSc, BSc Graduate Program in Physics The Ohio State University 2018 Dissertation Committee: Prof. Richard Furnstahl, Advisor Prof. Robert Perry Prof. Michael Lisa Prof. Junko Shigemitsu c Copyright by Alexander Signatur Dyhdalo 2018 Abstract Low-energy nuclear physics has seen a renaissance of activity recently with the advent of the nuclear effective field theory (EFT) approach, the power of renormalization group techniques, and advances in the computational cost-effectiveness and sophistication of quan- tum many-body methods. Nevertheless challenges remain in part from ambiguities of the nuclear Hamiltonian via regulator artifacts and the scaling of the many-body methods to heavier systems. Regulator artifacts arise due to a renormalization inconsistency in the nuclear EFT as currently formulated in Weinberg power counting, though their ultimate impact on nuclear observables is unknown at present. This results in a residual cutoff dependence in the EFT to all orders. We undertake an examination of these regulator artifacts using perturba- tive energy calculations of uniform matter as a testbed. Our methodology has found that the choice of regulator determines the shape of the energy phase space and that different regulators weight distinct phase space regions differently. Concerning many-body calculations, at present only phenomenological energy density functionals are able to solve for the full table of nuclides. However these functionals are currently unconnected to QCD and have no existing method for systematic improvement. -

An Assessment of Unequal Masses of Atoms Moving in Geometry of Two Component Fermion System
International Journal of Science and Advanced Innovative Research ISSN: 2536-7315 (Print) 2536-7323 (Online) Volume 5, Number 2, June 2020 http://www.casirmediapublishing.com AN ASSESSMENT OF UNEQUAL MASSES OF ATOMS MOVING IN GEOMETRY OF TWO COMPONENT FERMION SYSTEM ¹E. W. Likta, ²M. A. Abdul Azeez and 3 M. F. Haque ¹Department of Physics, University of Maiduguri, P.M.B 1069, Maiduguri, Borno State. ²Department of Physics Abubakar Tafawa Balewa University, Bauchi, P.M.B 0248, Bauchi, ¹E-Mail: [email protected] ABSTRACT The goal of this paper is to obtain the unequal masses of the atoms moving in geometry of two component fermions system. The two component fermions systems have been considered. The fermion-dimer scattering length 푎푓푑 and dimer- dimer scattering length 푎푑푑 in the universal limit of large fermion-fermion scattering length 푎푓푓 have been computed. The scattering properties of the fermion-dimer, dimer-dimer and the mass ratio dependence of the universal fermion-dimer and universal dimer-dimer scattering length have been analyzed. Scattering properties of composed system indicate a deep understanding of the dynamics in many-body of an atom system. Key word: Atoms, fermion-fermion, fermion-dimer, dimer-dimer and Hamiltonian INTRODUCTION In particle physics, a fermion is a particle that follows Fermi–Dirac statistics. These particles obey the Pauli Exclusion Principle. Fermions include all quarks and leptons, as well as all composite particles made of an odd number of these, such as all baryons and many atoms and nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. A fermion can be an elementary particle, such as the electron, or it can be a composite particle, such as the proton. -

BRITISH SCIENTISTS and the MANHATTAN PROJECT Also by Ferenc Morton Szasz
BRITISH SCIENTISTS AND THE MANHATTAN PROJECT Also by Ferenc Morton Szasz THE DIVIDED MIND OF PROTESTANT AMERICA RELIGION IN THE WEST (editor) THE DAY THE SUN ROSE TWICE: The Story of the Trinity Site Nuclear Explosion, July 16, 1945 THE PROTESTANT CLERGY IN THE GREAT PLAINS AND MOUNTAIN WEST British Scientists and the Manhattan Project The Los Alamos Years Ferenc Morton Szasz Professor of History University of New Mexico, Albuquerque MMACMILLAN © Ferenc Morton Szasz 1992 Softcover reprint of the hardcover 1st edition 1992 All rights reserved. No reproduction, copy or transmission of this publication may be made without written permission. No paragraph of this pub1ication may be reproduced, copied or transmitted save with written permission or in accordance with the provisions of the Copyright, Designs and Patents Act 1988, or under the terms of any 1icence permitting 1imited copying issued by the Copyright Licensing Agency, 33-4 A1fred P1ace, London WClE 7DP. Any person who does any unauthorised act in relation to this publication may be liab1e to crimina1 prosecution and civil claims for darnages. First published 1992 by MACMILLAN ACADEMIC AND PROFESSIONAL LTD. Houndmills, Basingstoke, Hampshire RG21 2XS andLondon Companies and representatives throughout the world ISBN 978-1-349-12733-7 ISBN 978-1-349-12731-3 (eBook) DOI 10.1007/978-1-349-12731-3 A catalogue record for this book is available from the British Library. For Margaret and Maria Contents Preface IX Introduction Xlll Background 2 The British Mission at Los Alamos: The Scientific -

A Nonlocal Quantum Engineer Contemplate but Don’T Forget to Calculate !
a nonlocal quantum engineer contemplate but don’t forget to calculate ! Reinhold A. Bertlmann Faculty of Physics, University of Vienna talk at symposium “ shut up and contemplate ! ” University of Vienna, March 3rd, 2017 engineer’s career at Harwell John Stewart Bell graduated at Queen’s University Belfast in experimental physics 1948 in mathematical physics 1949 high interest in quantum mechanics showing his dissatisfaction ! position at AERE Harwell from1949 on joined accelerator group of Walkinshaw (Malvern) William Walkinshaw: John on his new “Ariel” “ a young man of high caliber who showed his at Harwell 1952 independence … his mathematical talent was superb and elegant.” papers on electron and proton linear accelerators e.g. “basic algebra on strong focussing systems” “linear accelerator phase oscillations” “phase debunching by focussing foils in proton linear accelerator” Reinhold A. Bertlmann 2 turn to particle physics & Bohm’s qm in mid1950s Bell turned to nuclear and particle physics “time reversal in field theory …”, CPT theorem, PhD thesis fundamental ! “anomalous magnetic moments of nucleons”, collab. Tony Skyrme at that time paper of David Bohm appeared 1952 “interpretation of quantum theory in terms of hidden variable” Mary: for John a “revelation” “everything has definite properties” I remember John saying Bell’s talk about Bohm’s theory in TH division fierce debates with audience especially with Franz Mandl 1954 John married Mary Ross “mathematical engineer” accelerator physicist Reinhold A. Bertlmann 3 engineer’s job -

Skyrmions and Biskyrmions in Magnetic Films
City University of New York (CUNY) CUNY Academic Works Dissertations, Theses, and Capstone Projects CUNY Graduate Center 6-2021 Skyrmions and Biskyrmions in Magnetic Films Daniel Capic The Graduate Center, City University of New York How does access to this work benefit ou?y Let us know! More information about this work at: https://academicworks.cuny.edu/gc_etds/4286 Discover additional works at: https://academicworks.cuny.edu This work is made publicly available by the City University of New York (CUNY). Contact: [email protected] Skyrmions and Biskyrmions in Magnetic Films by Daniel Capic A dissertation submitted to the Graduate Faculty in Physics in partial fulfillment of the requirements for the degree of Doctor of Philosophy, The City University of New York 2021 ii c 2021 Daniel Capic All Rights Reserved iii Skyrmions and Biskyrmions in Magnetic Films by Daniel Capic This manuscript has been read and accepted by the Graduate Faculty in Physics in satisfaction of the dissertation requirement for the degree of Doctor of Philosophy. Date Eugene M. Chudnovsky Chair of Examining Committee Date Alexios Polychronakos Executive Officer Supervisory Committee: Dmitry A. Garanin Pouyan Ghaemi Andrew Kent Sergey Vitkalov The City University of New York iv Skyrmions and Biskyrmions in Magnetic Films by Daniel Capic Advisor: Distinguished Professor Eugene M. Chudnovsky Co-advisor: Professor Dmitry A. Garanin Skyrmions have garnered significant attention in condensed matter systems in recent years. In principle, they are topologically protected, so there is a large energy barrier preventing their annihilation. Furthermore, they can exist at the nanoscale, be manipulated with very small currents, and be created by a number of different methods. -
Skyrmion Behavior Revealed by Two X-Ray Studies J.C.T
MATERIALS / CONDENSED MATTER PUBLISHED BY THE ADVANCED LIGHT SOURCE COMMUNICATIONS GROUP Publications about this research: M.C. Langner, S. Roy, S.K. Mishra, Skyrmion Behavior Revealed by Two X-Ray Studies J.C.T. Lee, X.W. Shi, M.A. Hossain, Y.-D. Chuang, S. Seki, Y. Tokura, S.D. Kevan, and R.W. Schoenlein, Sometimes, the spins in a “Coupled Skyrmion Sublattices in magnetic material will form Cu2OSeO3,” Phys. Rev. Lett. 112, tiny swirls that can move 167202 (2014); J. Li, A. Tan, K.W. around like particles. The spins Moon, A. Doran, M.A. Marcus, A.T. Young, E. Arenholz, S. Ma, themselves stay put—it’s the R.F. Yang, C. Hwang, and Z.Q. Qiu, pattern that moves. These “Tailoring the topology of an quasiparticles have been artificial magnetic skyrmion,” Nat. dubbed “skyrmions,” after Commun. 5, 4704 (2014). British physicist Tony Skyrme, Research conducted by: M.C. who described their mathe- Langner and R.W. Schoenlein matics in a series of papers in (Berkeley Lab); S. Roy, S.K. the early 1960s. Now, over 50 Mishra, J.C.T. Lee, X.W. Shi, M.A. years later, scientists are Hossain, Y.-D. Chuang, A. Doran, intrigued by the possibility that M.A. Marcus, A.T. Young, and E. skyrmions could play a key role Arenholz (ALS); S. Seki (RIKEN in spintronics—electronics that and Japan Science and Technology employ spin to carry and mani- Agency); Y. Tokura (RIKEN and Univ. of Tokyo); S.D. Kevan (ALS upulate information. At the and Univ. of Oregon); J. Li, A. -

Proton - Wikipedia Page 1 of 10
Proton - Wikipedia Page 1 of 10 Proton From Wikipedia, the free encyclopedia + A proton is a subatomic particle, symbol p or p , with a Proton positive electric charge of +1e elementary charge and mass slightly less than that of a neutron. Protons and neutrons, each with masses of approximately one atomic mass unit, are collectively referred to as "nucleons". One or more protons are present in the nucleus of every atom. They are a necessary part of the nucleus. The number of protons in the nucleus is the defining property of an element, and is referred to as the atomic number (represented by the symbol Z). Since each element has a unique number of protons, each element has its own unique atomic number. The word proton is Greek for "first", and this name was given to the hydrogen nucleus by Ernest Rutherford in 1920. In previous years Rutherford had discovered that the hydrogen nucleus (known to be the lightest nucleus) could be extracted from the nuclei of nitrogen by collision. Protons were therefore a The quark structure of a proton. The color assignment of candidate to be a fundamental particle and a building block individual quarks is arbitrary, but all three colors must be of nitrogen and all other heavier atomic nuclei. present. Forces between quarks are mediated by gluons. In the modern Standard Model of particle physics, protons Classification Baryon are hadrons, and like neutrons, the other nucleon (particle Composition 2 up quarks, 1 down quark present in atomic nuclei), are composed of three quarks. Statistics Fermionic Although protons were originally considered fundamental or elementary particles, they are now known to be composed of Interactions Gravity, electromagnetic, weak, three valence quarks: two up quarks and one down quark.