Features Westward Ho! Musing on Mathematics and Mechanics Alan Champneys Cmath FIMA, University of Bristol
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

01 Freer.Pdf
John Henry Poynting First Prof Physics Birmingham 1880-1914 Rudolf Peierls 1907-1995 Birmingham 1937+ (holes in semiconductors) Marcus Laurence Elwin Oliphant 1901-2000 Birmingham 1937-1950 Otto Frisch (1904-1979) Bham 1939+ co-discover of 2H, 3H and 3He Role in first demonstration of nuclear fusion Got plans from Lawrence for Birmingham’s cyclotron John Bell 1928-1990 CPT 1951 Birmingham Luders-Pauli Thm Freeman-Dyson Tony Skyrme (1922-1987) Birmingham, 1949-51 Why are light nuclei so important – Understanding cutting edge theory ? [Otsuka et al., PRL 95 (05) 232502] Tensor correlations [Otsuka et al., PRL 97 (06) 162501] Neutron – proton interaction - - - + + + + - 8Be Ab initio type approaches (Greens Function Monte Carlo) 13 11 + 9 4 7 Ex [MeV] [MeV] Ex Ex 5 3 2+ 1 + -1 0 -1 4 9 14 19 24 Pieper and J(J+1) Wiringa, ANL 9 Ab initio no-core solutions for nuclear structure: Be P. Maris, C. Cockrell, M. Caprio and J.P. Vary Total density Proton - Neutron density Shows that one neutron provides a “ring ” cloud around two alpha clusters binding them together Chase Cockrell, ISU PhD student 12 C Chiral EFT on the lattice 32 S 24 Mg 9Be 9B PHYSICAL REVIEW C 86 , 057306 (2012), PHYSICAL REVIEW C 86 , 014312 (2012) 10 Be 12 C 10 C Characterization of 10 Be * Gas inlet LAMP array Window (2.5 um mylar) LAMP 6He LEDA LAMP LEDA Collimator M. Freer, et al. PRL 2006 Test of method- measure 10.36 MeV 4 + resonance In 16 O ( 12 C+ α) LAMP LEDA LAMP LEDA Resonances in 16 O E( 12 C)=16 MeV Singles Coincidence 10 10 4He Energy Energy (MeV) (MeV) 12 C 0 0 8 24 8 24 Angle Angle Gas pressure = 100 Torr LAMP LEDA LAMP 4 Energy ( 12 C) LEDA θcm ( He) 180 0 Energy ( 4He) 12 180 θcm ( C) Resonance analysis Counts 6000 - =121 mm detector 2000 - (E, θw) ddet window Distance/2+20 (mm) θw θlab dreaction 2 |P 4(cos( θcm )| θcm 6He+ 4He at 7.5 MeV – 7Li+ 7Li the 10.15 MeV state in 10 Be N. -

The Skyrme Model Fundamentals Methods Applications
springer.com Physics : Elementary Particles, Quantum Field Theory Makhankov, V.G., Rybakov, Y.P., Sanyuk, V.I. The Skyrme Model Fundamentals Methods Applications The December 1988 issue of the International Journal of Modern Physics A is dedicated to the memory of Tony Hilton Royle Skyrme. It contains an informative account of his life by Dalitz and Aitchison's reconstruction of a talk by Skyrme on the origin of the Skyrme model. From these pages, we learn that Tony Skyrme was born in England in December 1922. He grew up in that country during a period of increasing economic and political turbulence in Europe and elsewhere. In 1943, after Cambridge, he joined the British war effort in making the atomic bomb. He was associated with military projects throughout the war years and began his career as an academic theoretical physicist only in 1946. During 1946-61, he was associated with Cambridge, Birmingham and Harwell and was engaged in wide-ranging investigations in nuclear physics. It was this research which eventually culminated in his studies of nonlinear field theories and his remarkable proposals for the description of the nucleon as a chiral soliton. In his talk, Skyrme described the reasons behind his extraordinary sug• gestions, which Springer when first made must have seemed bizarre. According to him, ideas of this sort go back many Softcover reprint of the decades and occur in the work of Sir William Thomson, who later became Lord Kelvin. Skyrme 1st original 1st ed. 1993, XVIII, edition had heard of Kelvin in his youth. 265 p. Order online at springer.com/booksellers Springer Nature Customer Service Center LLC Printed book 233 Spring Street Softcover New York, NY 10013 Printed book USA Softcover T: +1-800-SPRINGER NATURE ISBN 978-3-642-84672-4 (777-4643) or 212-460-1500 [email protected] $ 109,99 Available Discount group Professional Books (2) Product category Monograph Series Springer Series in Nuclear and Particle Physics Other renditions Softcover ISBN 978-3-642-84671-7 Prices and other details are subject to change without notice. -

The Cambridge Mathematical Journal and Its Descendants: the Linchpin of a Research Community in the Early and Mid-Victorian Age ✩
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Historia Mathematica 31 (2004) 455–497 www.elsevier.com/locate/hm The Cambridge Mathematical Journal and its descendants: the linchpin of a research community in the early and mid-Victorian Age ✩ Tony Crilly ∗ Middlesex University Business School, Hendon, London NW4 4BT, UK Received 29 October 2002; revised 12 November 2003; accepted 8 March 2004 Abstract The Cambridge Mathematical Journal and its successors, the Cambridge and Dublin Mathematical Journal,and the Quarterly Journal of Pure and Applied Mathematics, were a vital link in the establishment of a research ethos in British mathematics in the period 1837–1870. From the beginning, the tension between academic objectives and economic viability shaped the often precarious existence of this line of communication between practitioners. Utilizing archival material, this paper presents episodes in the setting up and maintenance of these journals during their formative years. 2004 Elsevier Inc. All rights reserved. Résumé Dans la période 1837–1870, le Cambridge Mathematical Journal et les revues qui lui ont succédé, le Cambridge and Dublin Mathematical Journal et le Quarterly Journal of Pure and Applied Mathematics, ont joué un rôle essentiel pour promouvoir une culture de recherche dans les mathématiques britanniques. Dès le début, la tension entre les objectifs intellectuels et la rentabilité économique marqua l’existence, souvent précaire, de ce moyen de communication entre professionnels. Sur la base de documents d’archives, cet article présente les épisodes importants dans la création et l’existence de ces revues. 2004 Elsevier Inc. -

James Joseph Sylvester1
Chapter 8 JAMES JOSEPH SYLVESTER1 (1814-1897) James Joseph Sylvester was born in London, on the 3d of September, 1814. He was by descent a Jew. His father was Abraham Joseph Sylvester, and the future mathematician was the youngest but one of seven children. He received his elementary education at two private schools in London, and his secondary education at the Royal Institution in Liverpool. At the age of twenty he entered St. John’s College, Cambridge; and in the tripos examination he came out sec- ond wrangler. The senior wrangler of the year did not rise to any eminence; the fourth wrangler was George Green, celebrated for his contributions to mathe- matical physics; the fifth wrangler was Duncan F. Gregory, who subsequently wrote on the foundations of algebra. On account of his religion Sylvester could not sign the thirty-nine articles of the Church of England; and as a consequence he could neither receive the degree of Bachelor of Arts nor compete for the Smith’s prizes, and as a further consequence he was not eligible for a fellowship. To obtain a degree he turned to the University of Dublin. After the theological tests for degrees had been abolished at the Universities of Oxford and Cam- bridge in 1872, the University of Cambridge granted him his well-earned degree of Bachelor of Arts and also that of Master of Arts. On leaving Cambridge he at once commenced to write papers, and these were at first on applied mathematics. His first paper was entitled “An analytical development of Fresnel’s optical theory of crystals,” which was published in the Philosophical Magazine. -

Open Research Online Oro.Open.Ac.Uk
Open Research Online The Open University’s repository of research publications and other research outputs The Gender Gap in Mathematical and Natural Sciences from a Historical Perspective Conference or Workshop Item How to cite: Barrow-Green, June; Ponce Dawson, Silvina and Roy, Marie-Françoise (2019). The Gender Gap in Mathematical and Natural Sciences from a Historical Perspective. In: Proceedings of the International Congress of Mathematicians - 2018 (Sirakov, Boyan; Ney de Souza, Paulo and Viana, Marcelo eds.), World Scientific, pp. 1073–1092. For guidance on citations see FAQs. c [not recorded] https://creativecommons.org/licenses/by-nc-nd/4.0/ Version: Accepted Manuscript Link(s) to article on publisher’s website: http://dx.doi.org/doi:10.1142/11060 Copyright and Moral Rights for the articles on this site are retained by the individual authors and/or other copyright owners. For more information on Open Research Online’s data policy on reuse of materials please consult the policies page. oro.open.ac.uk P. I. C. M. – 2018 Rio de Janeiro, Vol. (1073–1068) 1 THE GENDER GAP IN MATHEMATICAL AND NATURAL 2 SCIENCES FROM A HISTORICAL PERSPECTIVE 3 J B-G, S P D M-F R 4 5 Abstract 6 The panel organised by the Committee for Women in Mathematics (CWM) 7 of the International Mathematical Union (IMU) took place at the International nd 8 Congress of Mathematicians (ICM) on August 2 , 2018. It was attended by about 9 190 people, with a reasonable gender balance (1/4 men, 3/4 women). The panel was 10 moderated by Caroline Series, President of the London Mathematical Society and 11 Vice-Chair of CWM. -

Topology in Physics-A Perspective
SU-4228-533 March 1993 TOPOLOGY IN PHYSICS - A PERSPECTIVE A.P. Balachandran Department of Physics, Syracuse University, Syracuse, NY 13244-1130 ABSTRACT This article, written in honour of Fritz Rohrlich, briefly surveys the role of topology in physics. arXiv:hep-th/9303177v1 31 Mar 1993 When I joined Syracuse University as a junior faculty member in September, 1964, Fritz Rohrlich was already there as a senior theoretician in the quantum field theory group. He was a very well-known physicist by that time, having made fundamental contributions to quantum field theory, and written his splendid book with Jauch. My generation of physicists grew up with Jauch and Rohrlich, and I was also familiar with Fritz’s research. It was therefore with a certain awe and a great deal of respect that I first made his acquaintance. Many years have passed since this first encounter. Our interests too have gradually evolved and changed in this intervening time. Starting from the late seventies or there- abouts, particle physicists have witnessed an increasing intrusion of topological ideas into their discipline. Our group at Syracuse has responded to this development by getting involved in soliton and monopole physics and in investigations on the role of topology in quantum physics. Meanwhile, especially during the last decade, there has been a per- ceptible shift in the direction of Fritz’s research to foundations and history of quantum physics. Later I will argue that topology affects the nature of wave functions (or more accurately of wave functions in the domains of observables) and has a profound meaning for the fundamentals of quantum theory. -
Quark•Gluon Plasma
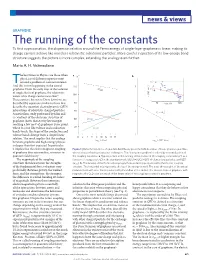
news & views GRAPHENE The running of the constants To first approximation, the dispersion relation around the Fermi energy of single-layer graphene is linear, making its charge carriers behave like massless relativistic subatomic particles. More careful inspection of its low-energy band structure suggests the picture is more complex, extending the analogy even further. Maria A. H. Vozmediano he best times in Physics are those when a α–1 b physicists of different expertise meet around a problem of common interest. 3 T ) And this is now happening in the case of 120 3 –1 α–1 2 graphene. From the early days of the isolation QED ms of single sheets of graphene, the relativistic 6 100 (10 1 F nature of its charge carriers was clear . v These carriers, known as Dirac fermions, are 1 described by equations similar to those that 80 10 E (meV) 100 describe the quantum electrodynamic (QED) interactions of relativistic charged particles. 60 2 U(1) ѵ ~ α–1 A meticulous study performed by Elias and F G 2 co-workers of the electronic structure of 40 SU(2) graphene shows that at very low energies reaching a few meV of graphene’s Dirac point, 20 where its cone-like valence and conduction SU(3) bands touch, the shape of the conduction and valence bands diverge from a simple linear 1 0 2 4 6 8 10 12 14 16 1 2 relation. The result implies that the analogy log E (Gev) log E (10–12 Gev) between graphene and high-energy physics 10 10 is deeper than first expected. -

Bertlmann – a Nonlocal Quantum Engineer
a nonlocal quantum engineer contemplate but don’t forget to calculate ! Reinhold A. Bertlmann Faculty of Physics, University of Vienna talk at symposium “ shut up and contemplate ! ” University of Vienna, March 3rd, 2017 engineer’s career at Harwell John Stewart Bell graduated at Queen’s University Belfast in experimental physics 1948 in mathematical physics 1949 high interest in quantum mechanics showing his dissatisfaction ! position at AERE Harwell from1949 on joined accelerator group of Walkinshaw (Malvern) William Walkinshaw: John on his new “Ariel” “ a young man of high caliber who showed his at Harwell 1952 independence … his mathematical talent was superb and elegant.” papers on electron and proton linear accelerators e.g. “basic algebra on strong focussing systems” “linear accelerator phase oscillations” “phase debunching by focussing foils in proton linear accelerator” Reinhold A. Bertlmann 2 turn to particle physics & Bohm’s qm in mid1950s Bell turned to nuclear and particle physics “time reversal in field theory …”, CPT theorem, PhD thesis fundamental ! “anomalous magnetic moments of nucleons”, collab. Tony Skyrme at that time paper of David Bohm appeared 1952 “interpretation of quantum theory in terms of hidden variable” Mary: for John a “revelation” “everything has definite properties” I remember John saying Bell’s talk about Bohm’s theory in TH division fierce debates with audience especially with Franz Mandl 1954 John married Mary Ross “mathematical engineer” accelerator physicist Reinhold A. Bertlmann 3 engineer’s job -

Aspects of the Many-Body Problem in Nuclear Physics
Aspects of the Many-Body Problem in Nuclear Physics DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Alexander Signatur Dyhdalo, MSc, BSc Graduate Program in Physics The Ohio State University 2018 Dissertation Committee: Prof. Richard Furnstahl, Advisor Prof. Robert Perry Prof. Michael Lisa Prof. Junko Shigemitsu c Copyright by Alexander Signatur Dyhdalo 2018 Abstract Low-energy nuclear physics has seen a renaissance of activity recently with the advent of the nuclear effective field theory (EFT) approach, the power of renormalization group techniques, and advances in the computational cost-effectiveness and sophistication of quan- tum many-body methods. Nevertheless challenges remain in part from ambiguities of the nuclear Hamiltonian via regulator artifacts and the scaling of the many-body methods to heavier systems. Regulator artifacts arise due to a renormalization inconsistency in the nuclear EFT as currently formulated in Weinberg power counting, though their ultimate impact on nuclear observables is unknown at present. This results in a residual cutoff dependence in the EFT to all orders. We undertake an examination of these regulator artifacts using perturba- tive energy calculations of uniform matter as a testbed. Our methodology has found that the choice of regulator determines the shape of the energy phase space and that different regulators weight distinct phase space regions differently. Concerning many-body calculations, at present only phenomenological energy density functionals are able to solve for the full table of nuclides. However these functionals are currently unconnected to QCD and have no existing method for systematic improvement. -

Forming the Analytical Society at Cambridge University
Forming the Analytical Society at Cambridge University Richard Stout Gordon College Wenham, MA The Analytical Society, an organization begun by students at Cambridge, was founded in 1812. Even though it was entirely student-led, the society was responsible for significant changes in the Cambridge mathematics curriculum and in the way mathematics was perceived in Britain throughout the nineteenth century. Its success was likely due to the outstanding students who formed the group, some of whom went on to become leaders in British science and mathematics for the next fifty years. In this paper we will briefly look at several of those who played important roles in forming and leading the society and we will consider the circumstances leading to its formation. In the fall of 1809, John Frederick William Herschel (1792 – 1871) matriculated at St. John’s College, one of the two largest colleges at Cambridge University. A serious student of mathematics, Herschel came from a privileged, upper-class family. When it didn’t work out for Herschel to be away at school, his family was able to hire a private tutor and allow Herschel to finish his education at home. Because his father, William Herschel, was a world-renowned astronomer--he discovered the planet Uranus--John Herschel likely grew up accustomed to scientific talk and held to high expectations. At Cambridge Herschel would distinguish himself as a superior student, finishing as the senior wrangler in 1813. After graduating from Cambridge Herschel was elected to the Royal Society and became a fellow of St. John’s. Although he continued to do mathematics for several years, primarily as an avocation, Herschel eventually followed in his father’s footsteps and became a distinguished astronomer. -

Early Indian Mathematical Pilgrims to Cambridge
Early Indian Mathematical Pilgrims to Cambridge K. Razi Naqvi Department of Physics, Norwegian University of Science and Technology N-7491 Trondheim, Norway During the nineteenth and the early part of the next century, the University of Cambridge (UoC) was the Mecca of Mathematcis for students from the British Isles and other parts of the British Empire. UoC concentrated on undergraduate teaching; its examination system, particularly the Mathematical Sciences Tripos (hereafter abbreviated as MathTrip), served as a launch pad for re- munerative and influential careers in law, church, politics, even medicine, and various adminis- trative organs of the British Raj. Most examiners were not engaged in research, and few examinees dreamt of qualifying as a high wrangler, or of becoming a creative mathematician. The purpose of this article is to scrutinise the performance of the few Indian students who completed one or both parts of MathTrip, the career choices they made after returning to India, and their efforts, if any, towards the diffusion of modern mathematics in Indian schools and colleges. Almost all of the returnees became functionaries of the colossal British bureaucracy. Rejuvenation of Indian math- ematics was carried out mostly by other enthusiasts, among whom Muslims are conspicuous by their scarcity. “Whether good mathematicians, when women and a handful of men from other they die, go to Cambridge, I do not parts of the British Empire were two mi- know. But it is well known that a large nority groups, whose members performed [?] number of men go there when they equally well. I am concerned here essen- are young for the purpose of being con- tially with those who came from the In- verted into senior wranglers and Smith’s dian subcontinent, and even out of this prizemen.” I would have been happier to small group, I will only speak of those who quote this remark if its author, the eccen- passed MathTrip during the period 1898– tric Oliver Heaviside, had used small in- 1909. -

Arthur Cayley1
Chapter 5 ARTHUR CAYLEY1 (1821-1895) Arthur Cayley was born at Richmond in Surrey, England, on August 16, 1821. His father, Henry Cayley, was descended from an ancient Yorkshire family, but had settled in St. Petersburg, Russia, as a merchant. His mother was Maria Antonia Doughty, a daughter of William Doughty; who, according to some writers, was a Russian; but her father’s name indicates an English origin. Arthur spent the first eight years of his life in St. Petersburg. In 1829 his parents took up their permanent abode at Blackheath, near London; and Arthur was sent to a private school. He early showed great liking for, and aptitude in, numerical calculations. At the age of 14 he was sent to King’s College School, London; the master of which, having observed indications of mathematical genius, advised the father to educate his son, not for his own business, as he had at first intended, but to enter the University of Cambridge. At the unusually early age of 17 Cayley began residence at Trinity College, Cambridge. As an undergraduate he had generally the reputation of being a mere mathematician; his chief diversion was novel-reading. He was also fond of travelling and mountain climbing, and was a member of the Alpine Club. The cause of the Analytical Society had now triumphed, and the Cambridge Mathematical Journal had been instituted by Gregory and Leslie Ellis. To this journal, at the age of twenty, Cayley contributed three papers, on subjects which had been suggested by reading the M´ecanique analytique of Lagrange and some of the works of Laplace.