DOCSLIB.ORG

Quantum Wells and Superlattices Come of Age

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Quantum Wells and Superlattices Come of Age Quantum Wells Feature Quantum wells and superlattices come of age Zh.l. Alferov A.F. loffe Physico-Technical Institute I Heterostructure quantum wells and superlattices have a pivotal role in the history of compound semi- conductors. This short review looks at the underlying physics, as well as the applications of quantum wells and superlattices. It starts by looking generally at the major developments in the field, before look- ing specifically at the advances made at the A.F. Ioffe Physico-Technical Institute in Russia. t he development of the its use in preparing room tempera- parabolic band would break into double-heterostructure (DH) tureAIGaAs DHS lasers in 1977. mini-bands separated by small for- T laser is a sensible starting Low dimensional semiconduc- bidden gaps and having Brillouin point for looking at the history of tor structures have formed a major zones determined by this period. heterostructure quantum wells. new branch of physics research. Similar ideas were described much Owing to electron confinement in Structures with such a small scale earlier by L.V. Keldysh in 1962 [3] DH, the double-heterostructure in one or two spatial dimensions, when considering the periodic po- laser became an important precur- their electronic properties are sig- tential produced on semiconduc- sor of in the development of quan- nificantly different from the same tor surface by intense ultrasonic tum well structures. This results material in its bulk form. These wave. from the fact that when the mid- properties are changed by quan- At the Physico-Technical dle-layer of these lasers had a thick- tum effects. A quantum well in Institute in St Petersburg in the ness of some hundred angstroms, which chargecarriers are restricted then Soviet Union, R. Kazarinov the electron levels would split to moving in two dimensions is an and R. Suris considered the theory because of the quantum-size example of such a structure. of current flow in superlattice effect. A clear manifestation of the structures in the beginning of the Further, the development of quantum-size effect in the optical 1970s [4].Their work revealed that epitaxial growth techniques for spectra of GaAs-AIGaAs semicon- the current between wells was de- these structures brought with it ductor heterostructures with ultra- termined by tunnelling through the ability to fabricate high-purity thin GaAs layer (quantum wells) the potential barriers separating and ultrathin layers that were to was demonstrated by Raymond the wells. It also predicted very im- become very important for quan- Dingle et al. in 1974 Ill. The au- portant phenomena: tunnelling un- tum wells. Two main methods of thors observed a characteristic der electric field when the ground growth with very precise control step-like behaviour in absorption state of a well coincides with an of thickness, planarity and other spectra and systematic shifts of the excited state of the next well and parameters were developed in characteristic energies with a stimulated emission resulting from 1970s -- molecular beam epitaxy quantum well width decrease. photon-assisted tunnelling be- (MBE) and metal organic chemical Experimental studies of super- tween the ground state of one well vapour deposition (MOCVD). MBE lattices, meanwhile, started after and excited state of a neighbour- was the first method to be of prac- the initial work of IBM scientists ing well, which is lower by the en- tical importance for III-V het- L.Esaki and R.Tsu in 1970 [2]. ergy due to applied electric field. erostructure technology, following These researchers considered elec- At that time L. Esaki and R. Tsu the pioneering work in the begin- tron transport in a superlattice i.e. independently considered reso- ning of 1970s by A. Cho at Bell at an additional periodic potential nant tunnelling in superlattice Laboratories. Not long after created by doping or changing the structures. MOCVD, which had its origins in composition of semiconductor ma- the early work of H. Manasevit, terials with the period bigger, but Superlattice structures found broad application in III-V comparable with, the lattice con- heterostructure research after stant of the crystal. In what Leo Pioneering experimental studies of R.Dupuis and PDapkus reported Esaki called a 'man-made crystal', a the superlattice structures were IIl-Vs Review• Vol.lO No. 7 1997 26 I I I I 80 lnGaAsP/GaAs W = 100 ~m k = 0.8 ~tm CW L= 1.2mm 70 NE 2 60 g 3 50 40 1--45-A757 2--3-A799 30 E // ] I I I I 20 0 1 2 3 4 5 1 (A) Figure 1: The CW light-current characteristics of InGaAsP/GaAs separate-confinement single quantum well DHS laser diodes. In (1), the diode had high and low reflective coatings, while in (2) the diode had a high reflective coating only. carried out by L.Esaki and R.Tsu very low concentration of defects. with the superlattices grown by Many years later in 1983, after vapour phase epitaxy (VPE) in a G.Osbourn's theoretical study at GaPxAsl x/GaAs system. At the Sandia lab and the first successful same time, in our own laboratory, preparation of a high quality the first multi-chamber apparatus strained-layer superlattice (GaAs/ for VPE was developed. As men- In0.2Ga0.sAs by M.Ludowise at tioned before, this was used to pre- Varian), N. Holonyak at the pare the superlattice structure University of Illinois achieved the GaP0.3As0.7/GaAs with the thick- first continuous wave (CW) room ness of each layer 100 A and total temperature laser action using number of the layers of 200. these structures. From research Observed peculiarities of the volt- such as this it became clear that in your age-current characteristics, their strained-layer superlattice the lat- temperature dependence and tice strain becomes an additional photoconductivity were explained degree of freedom.This meant that by the splitting of the conduc- by varying the layer thicknesses tion band due to the one-dimen- and compositions it was possible sional periodic potential of the to vary, continuously and indepen- superlattice. dently, the forbidden gap, lattice These first superlattices were constant and other parameters of also the first strained-layer super- the overall superlattice. lattices. E. Blakeslee and J. At the beginning of 1970s Matthews, who were working with L.Esaki and his co-workers started L. Esaki and R.Tsu at IBM, succeed- using MBE to study the AIGaAs sys- ed in the mid-1970s in growing tem resulting in the submission of strained-layer superlattices with a a paper in March 1974 to Physical Fax +46 46 t68g 81 WWW httpd/www.epigreSS.se Quantum Wells Feature Review on resonant tunnelling -- up to 420 GHz were reported in a application of the high-mobility, the First experimental demonstra- GaAs resonant tunnel diode at two-dimensional electron gas for tion of quantum well heterostruc- room temperature. microwave amplification. In 1980 ture physics. In the study, they The restriction of the motion of this led to new types of transistors measured the tunnelling current the electrons to two dimensions in based on single n-AIGaAs/n-GaAs and conductance as a function of field effect transistors has long modulation-doped heterostructure applied voltage in GaAs-Ga&lAs been recognized and was First veri- being developed.The development double barriers and found current fied, for the trapped electrons in occurred almost simultaneously in maxima associated with this reso- inversion layers, in a magneto-con- France, where they were labelled nant tunnelling. Later in the same ductance experiment conducted TEGFETs (two dimensional elec- year L.Esaki and L.L.Chang ob- by A.B.Fowler et al.. in 1,966. tron gas FETs), and in Japan, where served resonant tunnelling in a su- Spectral effects due to spatial they became known HEMTs (high perlattice. This strong interest in quantization were observed in thin electron mobility transistor). resonant tunnelling was obviously bismuth Films in 1968 by V.N. The first quantum well laser op- connected with its potential appli- Lutskii and L.A. Kulik at the eration was demonstrated by J.P. cations in high-speed electronics. Moscow Radio-Electronics Institute. van der Ziel et al.. in 1975, al- The success of these endeavours is Pioneering work on modula- though the parameters of the las- seen in the fact that by the end of tion-doped superlattices [5] ing were much worse than for the 1980s picosecond operation demonstrated a mobility enhance- average DHS lasers. By 1978, how- had been achieved in a double res- ment with respect to the bulk crys- ever, R. Dupuis and P.Dapkus, in onant tunnel diode and oscillations tal. This stimulated research on collaboration with N. Holonyak, were reporting quantum well lasers with parameters comparable (a) with their conventional DHS coun- terparts. Their paper was also no- table for its specific use of the • :."',/,i,~,~" ~ x",~: ,,, " ,,, term 'quantum well'. Even with this advance, it was not until 1982 that the real advantages of quan- -~ ,,~ tum well lasers were demonstrat- ed. At that time, W.TTsang at Bell Telephone Labs used the many im- provements of MBE growth tech- t=O nology, as well as an optimized (b) structure (GRIN SCH), to achieve threshold currents as low as 160 A. cm 2. The idea of stimulated emission in superlattices that had been pub- , ..: , •. lished by R.Kazarinov and R.Suris [4] back in 1971, was Fmally real- ized nearly a quarter of century lat- er after a proposal by Federico t = 15 min t = 6 min Capasso. The proposed structure was strongly improved and a cas- ~ .~ , ,: • ... ,!:.~,: :.:::. ;.': ,~: ::. -.... cade laser developed by E Capasso gave rise to the new generation of unipolar lasers operating in the ~,.
Load more

Recommended publications
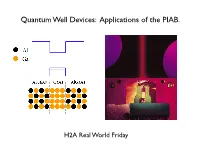
  • Quantum Well Devices: Applications of the PIAB
    Quantum Well Devices: Applications of the PIAB. H2A Real World Friday What is a semiconductor? no e- Conduction Band Empty e levels a few e- Empty e levels lots of e- Empty e levels Filled e levels Filled e levels Filled e levels Insulator Semiconductor Metal Electrons in the conduction band of semiconductors like Si or GaAs can move about freely. Conduction band a few e- Eg = hν Energy Bandgap in Valence band Filled e levels Semiconductors We can get electrons into the conduction band by either thermal excitation or light excitation (photons). Solar cells use semiconductors to convert photons to electrons. A "quantum well" structure made from AlGaAs-GaAs-AlGaAs creates a potential well for conduction electrons. 10-20 nm! A conduction electron that get trapped in a quantum well acts like a PIAB. A conduction electron that get trapped in a quantum well acts like a PIAB. Quantum Wells are used to make Laser Diodes Quantum Well Laser Diodes Quantum Wells are used to make Laser Diodes Quantum Well Laser Diodes Multiple Quantum Wells work even better. Multiple Quantum Well Laser Diodes Multiple Quantum Wells work even better. Multiple Quantum Well LEDs Multiple Quantum Wells work even better. Multiple Quantum Well Laser Diodes Multiple Quantum Wells also are used to make high efficiency Solar Cells. Quantum Well Solar Cells Multiple Quantum Wells also are used to make high efficiency Solar Cells. The most common approach to high efficiency photovoltaic power conversion is to partition the solar spectrum into separate bands and each absorbed by a cell specially tailored for that spectral band.
    [Show full text]
  • Dephasing in an Electronic Mach-Zehnder Interferometer,” Phys
    Dephasing and Quantum Noise in an electronic Mach-Zehnder Interferometer Dissertation zur Erlangung des Doktorgrades der Naturwissenschaften (Dr. rer. nat.) der Fakultät für Physik der Universität Regensburg vorgelegt von Andreas Helzel aus Kelheim Dezember 2012 ii Promotionsgesuch eingereicht am: 22.11.2012 Die Arbeit wurde angeleitet von: Prof. Dr. Christoph Strunk Prüfungsausschuss: Prof. Dr. G. Bali (Vorsitzender) Prof. Dr. Ch. Strunk (1. Gutachter) Dr. F. Pierre (2. Gutachter) Prof. Dr. F. Gießibl (weiterer Prüfer) iii In Gedenken an Maria Höpfl. Sie war die erste Taxifahrerin von Kelheim und wurde 100 Jahre alt. Contents 1. Introduction1 2. Basics 5 2.1. The two dimensional electron gas....................5 2.2. The quantum Hall effect - Quantized Landau levels...........8 2.3. Transport in the quantum Hall regime.................. 10 2.3.1. Quantum Hall edge states and Landauer-Büttiker formalism.. 10 2.3.2. Compressible and incompressible strips............. 14 2.3.3. Luttinger liquid in the QH regime at filling factor 2....... 16 2.4. Non-equilibrium fluctuations of a QPC.................. 24 2.5. Aharonov-Bohm Interferometry..................... 28 2.6. The electronic Mach-Zehnder interferometer............... 30 3. Measurement techniques 37 3.1. Cryostat and devices........................... 37 3.2. Measurement approach.......................... 39 4. Sample fabrication and characterization 43 4.1. Fabrication................................ 43 4.1.1. Material.............................. 43 4.1.2. Lithography............................ 44 4.1.3. Gold air bridges.......................... 45 4.1.4. Sample Design.......................... 46 4.2. Characterization.............................. 47 4.2.1. Filling factor........................... 47 4.2.2. Quantum point contacts..................... 49 4.2.3. Gate setting............................ 50 5. Characteristics of a MZI 51 5.1.
    [Show full text]
  • Bandgap-Engineered Hgcdte Infrared Detector Structures for Reduced Cooling Requirements
    Bandgap-Engineered HgCdTe Infrared Detector Structures for Reduced Cooling Requirements by Anne M. Itsuno A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy (Electrical Engineering) in The University of Michigan 2012 Doctoral Committee: Associate Professor Jamie D. Phillips, Chair Professor Pallab K. Bhattacharya Professor Fred L. Terry, Jr. Assistant Professor Kevin P. Pipe c Anne M. Itsuno 2012 All Rights Reserved To my parents. ii ACKNOWLEDGEMENTS First and foremost, I would like to thank my research advisor, Professor Jamie Phillips, for all of his guidance, support, and mentorship throughout my career as a graduate student at the University of Michigan. I am very fortunate to have had the opportunity to work alongside him. I sincerely appreciate all of the time he has taken to meet with me to discuss and review my research work. He is always very thoughtful and respectful of his students, treating us as peers and valuing our opinions. Professor Phillips has been a wonderful inspiration to me. I have learned so much from him, and I believe he truly exemplifies the highest standard of teacher and technical leader. I would also like to acknowledge the past and present members of the Phillips Research Group for their help, useful discussions, and camaraderie. In particular, I would like to thank Dr. Emine Cagin for her constant encouragement and humor. Emine has been a wonderful role model. I truly admire her expertise, her accom- plishments, and her unfailing optimism and can only hope to follow in her footsteps. I would also like to thank Dr.
    [Show full text]
  • Optimizing Fabrication and Modeling of Quantum Dot Superlattice for Fets and Nonvolatile Memories Pial Mirdha University of Connecticut - Storrs, [email protected]
    University of Connecticut OpenCommons@UConn Doctoral Dissertations University of Connecticut Graduate School 12-12-2017 Optimizing Fabrication and Modeling of Quantum Dot Superlattice for FETs and Nonvolatile Memories Pial Mirdha University of Connecticut - Storrs, [email protected] Follow this and additional works at: https://opencommons.uconn.edu/dissertations Recommended Citation Mirdha, Pial, "Optimizing Fabrication and Modeling of Quantum Dot Superlattice for FETs and Nonvolatile Memories" (2017). Doctoral Dissertations. 1686. https://opencommons.uconn.edu/dissertations/1686 Optimizing Fabrication and Modeling of Quantum Dot Superlattice for FETs and Nonvolatile Memories Pial Mirdha PhD University of Connecticut 2017 Quantum Dot Superlattice (QDSL) are novel structures which can be applied to transis- tors and memory devices to produce unique current voltage characteristics. QDSL are made of Silicon and Germanium with an inner intrinsic layer surrounded by their respective oxides and in the single digit nanometer range. When used in transistors they have shown to induce 3 to 4 states for Multi-Valued Logic (MVL). When applied to memory they have been demonstrated to retain 2 bits of charge which instantly double the memory density. For commercial application they must produce consistent and repeatable current voltage characteristics, the current QDSL structures consist of only two layers of quantum dots which is not a robust design. This thesis demonstrates the utility of using QDSL by designing MVL circuit which consume less power while still producing higher computational speed when compared to conventional cmos based circuits. Additionally, for reproducibility and stability of current voltage characteristics, a novel 4 layer of both single and mixed quantum dots are demonstrated.
    [Show full text]
  • Modeling Multiple Quantum Well and Superlattice Solar Cells
    Natural Resources, 2013, 4, 235-245 235 http://dx.doi.org/10.4236/nr.2013.43030 Published Online July 2013 (http://www.scirp.org/journal/nr) Modeling Multiple Quantum Well and Superlattice Solar Cells Carlos I. Cabrera1, Julio C. Rimada2, Maykel Courel2,3, Luis Hernandez4,5, James P. Connolly6, Agustín Enciso4, David A. Contreras-Solorio4 1Department of Physics, University of Pinar del Río, Pinar del Río, Cuba; 2Solar Cell Laboratory, Institute of Materials Science and Technology (IMRE), University of Havana, Havana, Cuba; 3Higher School in Physics and Mathematics, National Polytechnic Insti- tute, Mexico City, Mexico; 4Academic Unit of Physics, Autonomous University of Zacatecas, Zacatecas, México; 5Faculty of Phys- ics, University of Havana, La Habana, Cuba; 6Nanophotonics Technology Center, Universidad Politécnica de Valencia, Valencia, Spain. Email: [email protected] Received January 23rd, 2013; revised May 14th, 2013; accepted May 27th, 2013 Copyright © 2013 Carlos I. Cabrera et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT The inability of a single-gap solar cell to absorb energies less than the band-gap energy is one of the intrinsic loss mechanisms which limit the conversion efficiency in photovoltaic devices. New approaches to “ultra-high” efficiency solar cells include devices such as multiple quantum wells (QW) and superlattices (SL) systems in the intrinsic region of a p-i-n cell of wider band-gap energy (barrier or host) semiconductor. These configurations are intended to extend the absorption band beyond the single gap host cell semiconductor.
    [Show full text]
  • Chapter 2 Quantum Theory
    Chapter 2 - Quantum Theory At the end of this chapter – the class will: Have basic concepts of quantum physical phenomena and a rudimentary working knowledge of quantum physics Have some familiarity with quantum mechanics and its application to atomic theory Quantization of energy; energy levels Quantum states, quantum number Implication on band theory Chapter 2 Outline Basic concept of quantization Origin of quantum theory and key quantum phenomena Quantum mechanics Example and application to atomic theory Concept introduction The quantum car Imagine you drive a car. You turn on engine and it immediately moves at 10 m/hr. You step on the gas pedal and it does nothing. You step on it harder and suddenly, the car moves at 40 m/hr. You step on the brake. It does nothing until you flatten the brake with all your might, and it suddenly drops back to 10 m/hr. What’s going on? Continuous vs. Quantization Consider a billiard ball. It requires accuracy and precision. You have a cue stick. Assume for simplicity that there is no friction loss. How fast can you make the ball move using the cue stick? How much kinetic energy can you give to the ball? The Newtonian mechanics answer is: • any value, as much as energy as you can deliver. The ball can be made moving with 1.000 joule, or 3.1415926535 or 0.551 … joule. Supposed it is moving with 1-joule energy, you can give it an extra 0.24563166 joule by hitting it with the cue stick by that amount of energy.
    [Show full text]
  • Chapter 2 Semiconductor Heterostructures
    Semiconductor Optoelectronics (Farhan Rana, Cornell University) Chapter 2 Semiconductor Heterostructures 2.1 Introduction Most interesting semiconductor devices usually have two or more different kinds of semiconductors. In this handout we will consider four different kinds of commonly encountered heterostructures: a) pn heterojunction diode b) nn heterojunctions c) pp heterojunctions d) Quantum wells, quantum wires, and quantum dots 2.2 A pn Heterojunction Diode Consider a junction of a p-doped semiconductor (semiconductor 1) with an n-doped semiconductor (semiconductor 2). The two semiconductors are not necessarily the same, e.g. 1 could be AlGaAs and 2 could be GaAs. We assume that 1 has a wider band gap than 2. The band diagrams of 1 and 2 by themselves are shown below. Vacuum level q1 Ec1 q2 Ec2 Ef2 Eg1 Eg2 Ef1 Ev2 Ev1 2.2.1 Electron Affinity Rule and Band Alignment: How does one figure out the relative alignment of the bands at the junction of two different semiconductors? For example, in the Figure above how do we know whether the conduction band edge of semiconductor 2 should be above or below the conduction band edge of semiconductor 1? The answer can be obtained if one measures all band energies with respect to one value. This value is provided by the vacuum level (shown by the dashed line in the Figure above). The vacuum level is the energy of a free electron (an electron outside the semiconductor) which is at rest with respect to the semiconductor. The electron affinity, denoted by (units: eV), of a semiconductor is the energy required to move an electron from the conduction band bottom to the vacuum level and is a material constant.
    [Show full text]
  • Sankar Das Sarma 3/11/19 1 Curriculum Vitae
    Sankar Das Sarma 3/11/19 Curriculum Vitae Sankar Das Sarma Richard E. Prange Chair in Physics and Distinguished University Professor Director, Condensed Matter Theory Center Fellow, Joint Quantum Institute University of Maryland Department of Physics College Park, Maryland 20742-4111 Email: [email protected] Web page: www.physics.umd.edu/cmtc Fax: (301) 314-9465 Telephone: (301) 405-6145 Published articles in APS journals I. Physical Review Letters 1. Theory for the Polarizability Function of an Electron Layer in the Presence of Collisional Broadening Effects and its Experimental Implications (S. Das Sarma) Phys. Rev. Lett. 50, 211 (1983). 2. Theory of Two Dimensional Magneto-Polarons (S. Das Sarma), Phys. Rev. Lett. 52, 859 (1984); erratum: Phys. Rev. Lett. 52, 1570 (1984). 3. Proposed Experimental Realization of Anderson Localization in Random and Incommensurate Artificial Structures (S. Das Sarma, A. Kobayashi, and R.E. Prange) Phys. Rev. Lett. 56, 1280 (1986). 4. Frequency-Shifted Polaron Coupling in GaInAs Heterojunctions (S. Das Sarma), Phys. Rev. Lett. 57, 651 (1986). 5. Many-Body Effects in a Non-Equilibrium Electron-Lattice System: Coupling of Quasiparticle Excitations and LO-Phonons (J.K. Jain, R. Jalabert, and S. Das Sarma), Phys. Rev. Lett. 60, 353 (1988). 6. Extended Electronic States in One Dimensional Fibonacci Superlattice (X.C. Xie and S. Das Sarma), Phys. Rev. Lett. 60, 1585 (1988). 1 Sankar Das Sarma 7. Strong-Field Density of States in Weakly Disordered Two Dimensional Electron Systems (S. Das Sarma and X.C. Xie), Phys. Rev. Lett. 61, 738 (1988). 8. Mobility Edge is a Model One Dimensional Potential (S.
    [Show full text]
  • Field Effect Transistors
    Introduction to Nanoelectronics Part 5. Field Effect Transistors Field Effect transistors (FETs) are the backbone of the electronics industry. The remarkable progress of electronics over the last few decades is due in large part to advances in FET technology, especially their miniaturization, which has improved speed, decreased power consumption and enabled the fabrication of more complex circuits. Consequently, engineers have worked to roughly double the number of FETs in a complex chip such as an integrated circuit every 1.5-2 years; see Fig. 1 in the Introduction. This trend, known now as Moore‟s law, was first noted in 1965 by Gordon Moore, an Intel engineer. We will address Moore‟s law and its limits specifically at the end of the class. But for now, we simply note that FETs are already small and getting smaller. Intel‟s latest processors have a source-drain separation of approximately 65nm. In this section we will first look at the simplest FETs: molecular field effect transistors. We will use these devices to explain field effect switching. Then, we will consider ballistic quantum wire FETs, ballistic quantum well FETs and ultimately non-ballistic macroscopic FETs. (i) Molecular FETs The architecture of a molecular field effect transistor is shown in Fig. 5.1. The molecule bridges the source and drain contact providing a channel for electrons to flow. There is also a third terminal positioned close to the conductor. This contact is known as the gate, as it is intended to control the flow of charge through the channel. The gate does not inject charge directly.
    [Show full text]
  • Quantum Confinement
    QUANTUM DOTS Quantum Confinement Gopal Ramalingam1, Poopathy Kathirgamanathan 2, Ganesan Ravi3, Thangavel Elangovan4, Bojarajan Arjun kumar 5, Nadarajah Manivannan6, Kasinathan Kaviyarasu7 1,5Deapartment of Nanoscience and Technology, Alagappa University, karaikudi- 630003, Tamil Nadu. email: [email protected] 2Department of Chemical and Materials Engineering, Brunel University London, Uxbridge, UB8PH, UK 3Deapartment of Physics, Alagappa University, karaikudi-630 003, Tamil Nadu 4Department of Energy Science, Periyar University, Salem -636 011, Tamil Nadu, India 6 Design, Brunel University London, Uxbridge UB8 3PH, UK. 7UNESCO-UNISA Africa Chair in Nanoscience's/Nanotechnology Laboratories, College of Graduate Studies, University of South Africa (UNISA), Muckleneuk Ridge, P O Box 392, Pretoria, South Africa. 7Nanosciences African network (NANOAFNET), Materials Research Group (MRG), iThemba LABS-National Research Foundation (NRF), 1 Old Faure Road, 7129, P O Box722, Somerset West, Western Cape Province, South Africa Abstract Quantum Confinement is the spatial confinement of electron-hole pairs (excitons) in one or more dimensions within a material and also electronic energy levels are discrete. It is due to the confinement of the electronic wave function to the physical dimensions of the particles. Furthermore this can be divided in to three ways: 1D confinement (free carrier in a plane) -Quantum Wells, 2D confinement (carriers are free to move down) - Quantum Wire and 3D-confinement (carriers are confined in all directions) are discussed in details. In addition the formation mechanism of exciton, quantum confinement behaviour of strong, moderate and week confinement have been discussed below. Keywords: Quantum dots; Energy level; Exciton; Confinement; Bohr radius; 1. Introduction of Quantum confinement The term ‘quantum confinement’ is mainly deals with energy of confined electrons (electrons or electron-hole).
    [Show full text]
  • Quasicrystalline 30 Twisted Bilayer Graphene As an Incommensurate
    Quasicrystalline 30◦ twisted bilayer graphene as an incommensurate superlattice with strong interlayer coupling Wei Yaoa,b, Eryin Wanga,b, Changhua Baoa,b, Yiou Zhangc, Kenan Zhanga,b, Kejie Baoc, Chun Kai Chanc, Chaoyu Chend, Jose Avilad, Maria C. Asensiod,e, Junyi Zhuc,1, and Shuyun Zhoua,b,f,1 aState Key Laboratory of Low Dimensional Quantum Physics, Tsinghua University, Beijing 100084, China; bDepartment of Physics, Tsinghua University, Beijing 100084, China; cDepartment of Physics, The Chinese University of Hong Kong, Hong Kong, China; dSynchrotron SOLEIL, L’Orme des Merisiers, Saint Aubin-BP 48, 91192 Gif sur Yvette Cedex, France; eUniversite´ Paris-Saclay, L’Orme des Merisiers, Saint Aubin-BP 48, 91192 Gif sur Yvette Cedex, France; and fCollaborative Innovation Center of Quantum Matter, Beijing 100084, P. R. China Edited by Hongjie Dai, Department of Chemistry, Stanford University, Stanford, CA, and approved May 25, 2018 (received for review December 1, 2017) The interlayer coupling can be used to engineer the electronic Although the electronic structures of commensurate het- structure of van der Waals heterostructures (superlattices) to erostructures have been investigated in recent years (13–17), obtain properties that are not possible in a single material. So research on incommensurate heterostructures remains limited far research in heterostructures has been focused on commen- for two reasons. On one hand, incommensurate heterostruc- surate superlattices with a long-ranged Moire´ period. Incom- tures are difficult to be stabilized, and thus, they are quite mensurate heterostructures with rotational symmetry but not rare under natural growth conditions. On the other hand, translational symmetry (in analogy to quasicrystals) are not only it is usually assumed that the interlayer interaction is sup- rare in nature, but also the interlayer interaction has often been pressed due to the lack of phase coherence.
    [Show full text]
  • Optical Physics of Quantum Wells
    Optical Physics of Quantum Wells David A. B. Miller Rm. 4B-401, AT&T Bell Laboratories Holmdel, NJ07733-3030 USA 1 Introduction Quantum wells are thin layered semiconductor structures in which we can observe and control many quantum mechanical effects. They derive most of their special properties from the quantum confinement of charge carriers (electrons and "holes") in thin layers (e.g 40 atomic layers thick) of one semiconductor "well" material sandwiched between other semiconductor "barrier" layers. They can be made to a high degree of precision by modern epitaxial crystal growth techniques. Many of the physical effects in quantum well structures can be seen at room temperature and can be exploited in real devices. From a scientific point of view, they are also an interesting "laboratory" in which we can explore various quantum mechanical effects, many of which cannot easily be investigated in the usual laboratory setting. For example, we can work with "excitons" as a close quantum mechanical analog for atoms, confining them in distances smaller than their natural size, and applying effectively gigantic electric fields to them, both classes of experiments that are difficult to perform on atoms themselves. We can also carefully tailor "coupled" quantum wells to show quantum mechanical beating phenomena that we can measure and control to a degree that is difficult with molecules. In this article, we will introduce quantum wells, and will concentrate on some of the physical effects that are seen in optical experiments. Quantum wells also have many interesting properties for electrical transport, though we will not discuss those here.
    [Show full text]