DOCSLIB.ORG

Supplementary Lecture Notes: Quantum Mechanics Made Simple

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Supplementary Lecture Notes: Quantum Mechanics Made Simple Quantum Mechanics Made Simple: Lecture Notes Weng Cho CHEW1 October 5, 2012 1The author is with U of Illinois, Urbana-Champaign. He works part time at Hong Kong U this summer. Contents Preface vii Acknowledgements vii 1 Introduction 1 1.1 Introduction . .1 1.2 Quantum Mechanics is Bizarre . .2 1.3 The Wave Nature of a Particle{Wave Particle Duality . .2 2 Classical Mechanics 7 2.1 Introduction . .7 2.2 Lagrangian Formulation . .8 2.3 Hamiltonian Formulation . 10 2.4 More on Hamiltonian . 12 2.5 Poisson Bracket . 12 3 Quantum Mechanics|Some Preliminaries 15 3.1 Introduction . 15 3.2 Probabilistic Interpretation of the wavefunction . 16 3.3 Simple Examples of Time Independent Schr¨odingerEquation . 19 3.3.1 Particle in a 1D Box . 19 3.3.2 Particle Scattering by a Barrier . 21 3.3.3 Particle in a Potential Well . 21 3.4 The Quantum Harmonic Oscillator . 23 4 Time-Dependent Schr¨odingerEquation 27 4.1 Introduction . 27 4.2 Quantum States in the Time Domain . 27 4.3 Coherent State . 28 4.4 Measurement Hypothesis and Expectation Value . 29 4.4.1 Time Evolution of the Hamiltonian Operator . 31 4.4.2 Uncertainty Principle . 32 4.4.3 Particle Current . 32 i ii Quantum Mechanics Made Simple 5 Mathematical Preliminaries 35 5.1 A Function is a Vector . 35 5.2 Operators . 38 5.2.1 Matrix Representation of an Operator . 38 5.2.2 Bilinear Expansion of an Operator . 39 5.2.3 Trace of an Operator . 39 5.2.4 Unitary Operators . 41 5.2.5 Hermitian Operators . 42 5.3 Identity Operator in a Continuum Space . 44 5.4 Changing Between Representations . 47 5.4.1 The Coordinate Basis Function . 48 5.5 Commutation of Operators . 49 5.6 Expectation Value and Eigenvalue of Operators . 49 5.7 Generalized Uncertainty Principle . 51 5.8 Time Evolution of the Expectation Value of an Operator . 53 5.9 Periodic Boundary Condition . 54 6 Approximate Methods in Quantum Mechanics 57 6.1 Introduction . 57 6.2 Use of an Approximate Subspace . 57 6.3 Time Independent Perturbation Theory . 59 6.4 Tight Binding Model . 64 6.4.1 Variational Method . 66 6.4.2 Time Dependent Perturbation Theory . 67 7 Quantum Mechanics in Crystals 71 7.1 Introduction . 71 7.2 Bloch-Floquet Waves . 72 7.3 Bloch-Floquet Theorem for 3D . 74 7.4 Effective Mass Schr¨odingerEquation . 78 7.5 Density of States (DOS) . 79 7.6 DOS in a Quantum Well . 81 8 Angular Momentum 85 8.1 Introduction . 85 8.1.1 Electron Trapped in a Pill Box . 86 8.1.2 Electron Trapped in a Spherical Box . 88 8.2 Mathematics of Angular Momentum . 91 8.3 L^2 Operator . 92 Contents iii 9 Spin 95 9.1 Introduction . 95 9.2 Spin Operators . 95 9.3 The Bloch Sphere . 97 9.4 Spinor . 98 9.5 Pauli Equation . 99 10 Identical Particles 101 10.1 Introduction . 101 10.2 Pauli Exclusion Principle . 102 10.3 Exchange Energy . 102 10.4 Extension to More Than Two Particles . 104 10.5 Counting the Number of Basis states . 105 10.6 Examples . 106 10.7 Thermal Distribution Functions . 107 11 Density Matrix 111 11.1 Pure and Mixed States . 111 11.2 Density Operator . 112 11.3 Time Evolution of the Matrix Element of an Operator . 114 11.4 Interaction of Light with Two-Level Atomic System . 115 12 Quantization of Classical Fields 123 12.1 Introduction . 123 12.2 The Quantum Harmonic Oscillator Revisited . 124 12.2.1 Eigenfunction by the Ladder Approach . 126 12.3 Quantization of Waves on a Linear Atomic Chain{Phonons . 127 12.4 Schr¨odingerPicture versus Heisenberg Picture . 132 12.5 The Continuum Limit . 133 12.6 Quantization of Electromagnetic Field . 136 12.6.1 Hamiltonian . 137 12.6.2 Field Operators . 138 12.6.3 Multimode Case and Fock State . 139 12.6.4 One-Photon State . 140 12.6.5 Coherent State Revisited . 141 13 Schr¨odingerWave Fields 145 13.1 Introduction . 145 13.2 Fock Space for Fermions . 145 13.3 Field Operators . 147 13.4 Similarity Transform . 149 13.5 Additive One-Particle Operator . 150 13.5.1 Three-Particle Case . 151 13.6 Additive Two-Particle Operator . 153 13.7 More on Field Operators . 155 iv Quantum Mechanics Made Simple 13.8 Boson Wave Field . 157 13.9 Boson Field Operators . 158 13.10Additive One-Particle Operator . 159 13.11The Difference between Boson Field and Photon Field . 160 14 Interaction of Different Particles 161 14.1 Introduction . 161 14.2 Interaction of Particles . 161 14.3 Time-Dependent Perturbation Theory . 162 14.3.1 Absorption . 163 14.4 Spontaneous Emission . 165 14.5 Stimulated Emission . 165 14.6 Multi-photon Case . 167 14.7 Total Spontaneous Emission Rate . 167 15 Quantum Information and Quantum Interpretation 169 15.1 Introduction . 169 15.2 Quantum Cryptography . 169 15.2.1 No-cloning Theorem . 169 15.2.2 Entangled States . 170 15.2.3 A Simple.
Load more

Recommended publications
  • The Second Quantized Approach to the Study of Model Hamiltonians in Quantum Hall Regime
    Washington University in St. Louis Washington University Open Scholarship Arts & Sciences Electronic Theses and Dissertations Arts & Sciences Winter 12-15-2016 The Second Quantized Approach to the Study of Model Hamiltonians in Quantum Hall Regime Li Chen Washington University in St. Louis Follow this and additional works at: https://openscholarship.wustl.edu/art_sci_etds Recommended Citation Chen, Li, "The Second Quantized Approach to the Study of Model Hamiltonians in Quantum Hall Regime" (2016). Arts & Sciences Electronic Theses and Dissertations. 985. https://openscholarship.wustl.edu/art_sci_etds/985 This Dissertation is brought to you for free and open access by the Arts & Sciences at Washington University Open Scholarship. It has been accepted for inclusion in Arts & Sciences Electronic Theses and Dissertations by an authorized administrator of Washington University Open Scholarship. For more information, please contact [email protected]. WASHINGTON UNIVERSITY IN ST. LOUIS Department of Physics Dissertation Examination Committee: Alexander Seidel, Chair Zohar Nussinov Michael Ogilvie Xiang Tang Li Yang The Second Quantized Approach to the Study of Model Hamiltonians in Quantum Hall Regime by Li Chen A dissertation presented to The Graduate School of Washington University in partial fulfillment of the requirements for the degree of Doctor of Philosophy December 2016 Saint Louis, Missouri c 2016, Li Chen ii Contents List of Figures v Acknowledgements vii Abstract viii 1 Introduction to Quantum Hall Effect 1 1.1 The classical Hall effect . .1 1.2 The integer quantum Hall effect . .3 1.3 The fractional quantum Hall effect . .7 1.4 Theoretical explanations of the fractional quantum Hall effect . .9 1.5 Laughlin's gedanken experiment .
    [Show full text]
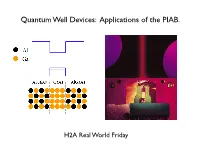
  • Quantum Well Devices: Applications of the PIAB
    Quantum Well Devices: Applications of the PIAB. H2A Real World Friday What is a semiconductor? no e- Conduction Band Empty e levels a few e- Empty e levels lots of e- Empty e levels Filled e levels Filled e levels Filled e levels Insulator Semiconductor Metal Electrons in the conduction band of semiconductors like Si or GaAs can move about freely. Conduction band a few e- Eg = hν Energy Bandgap in Valence band Filled e levels Semiconductors We can get electrons into the conduction band by either thermal excitation or light excitation (photons). Solar cells use semiconductors to convert photons to electrons. A "quantum well" structure made from AlGaAs-GaAs-AlGaAs creates a potential well for conduction electrons. 10-20 nm! A conduction electron that get trapped in a quantum well acts like a PIAB. A conduction electron that get trapped in a quantum well acts like a PIAB. Quantum Wells are used to make Laser Diodes Quantum Well Laser Diodes Quantum Wells are used to make Laser Diodes Quantum Well Laser Diodes Multiple Quantum Wells work even better. Multiple Quantum Well Laser Diodes Multiple Quantum Wells work even better. Multiple Quantum Well LEDs Multiple Quantum Wells work even better. Multiple Quantum Well Laser Diodes Multiple Quantum Wells also are used to make high efficiency Solar Cells. Quantum Well Solar Cells Multiple Quantum Wells also are used to make high efficiency Solar Cells. The most common approach to high efficiency photovoltaic power conversion is to partition the solar spectrum into separate bands and each absorbed by a cell specially tailored for that spectral band.
    [Show full text]
  • Canonical Quantization of Two-Dimensional Gravity S
    Journal of Experimental and Theoretical Physics, Vol. 90, No. 1, 2000, pp. 1–16. Translated from Zhurnal Éksperimental’noœ i Teoreticheskoœ Fiziki, Vol. 117, No. 1, 2000, pp. 5–21. Original Russian Text Copyright © 2000 by Vergeles. GRAVITATION, ASTROPHYSICS Canonical Quantization of Two-Dimensional Gravity S. N. Vergeles Landau Institute of Theoretical Physics, Russian Academy of Sciences, Chernogolovka, Moscow oblast, 142432 Russia; e-mail: [email protected] Received March 23, 1999 Abstract—A canonical quantization of two-dimensional gravity minimally coupled to real scalar and spinor Majorana fields is presented. The physical state space of the theory is completely described and calculations are also made of the average values of the metric tensor relative to states close to the ground state. © 2000 MAIK “Nauka/Interperiodica”. 1. INTRODUCTION quantization) for observables in the highest orders, will The quantum theory of gravity in four-dimensional serve as a criterion for the correctness of the selected space–time encounters fundamental difficulties which quantization route. have not yet been surmounted. These difficulties can be The progress achieved in the construction of a two- arbitrarily divided into conceptual and computational. dimensional quantum theory of gravity is associated The main conceptual problem is that the Hamiltonian is with two ideas. These ideas will be formulated below a linear combination of first-class constraints. This fact after the necessary notation has been introduced. makes the role of time in gravity unclear. The main computational problem is the nonrenormalizability of We shall postulate that space–time is topologically gravity theory. These difficulties are closely inter- equivalent to a two-dimensional cylinder.
    [Show full text]
  • Dephasing in an Electronic Mach-Zehnder Interferometer,” Phys
    Dephasing and Quantum Noise in an electronic Mach-Zehnder Interferometer Dissertation zur Erlangung des Doktorgrades der Naturwissenschaften (Dr. rer. nat.) der Fakultät für Physik der Universität Regensburg vorgelegt von Andreas Helzel aus Kelheim Dezember 2012 ii Promotionsgesuch eingereicht am: 22.11.2012 Die Arbeit wurde angeleitet von: Prof. Dr. Christoph Strunk Prüfungsausschuss: Prof. Dr. G. Bali (Vorsitzender) Prof. Dr. Ch. Strunk (1. Gutachter) Dr. F. Pierre (2. Gutachter) Prof. Dr. F. Gießibl (weiterer Prüfer) iii In Gedenken an Maria Höpfl. Sie war die erste Taxifahrerin von Kelheim und wurde 100 Jahre alt. Contents 1. Introduction1 2. Basics 5 2.1. The two dimensional electron gas....................5 2.2. The quantum Hall effect - Quantized Landau levels...........8 2.3. Transport in the quantum Hall regime.................. 10 2.3.1. Quantum Hall edge states and Landauer-Büttiker formalism.. 10 2.3.2. Compressible and incompressible strips............. 14 2.3.3. Luttinger liquid in the QH regime at filling factor 2....... 16 2.4. Non-equilibrium fluctuations of a QPC.................. 24 2.5. Aharonov-Bohm Interferometry..................... 28 2.6. The electronic Mach-Zehnder interferometer............... 30 3. Measurement techniques 37 3.1. Cryostat and devices........................... 37 3.2. Measurement approach.......................... 39 4. Sample fabrication and characterization 43 4.1. Fabrication................................ 43 4.1.1. Material.............................. 43 4.1.2. Lithography............................ 44 4.1.3. Gold air bridges.......................... 45 4.1.4. Sample Design.......................... 46 4.2. Characterization.............................. 47 4.2.1. Filling factor........................... 47 4.2.2. Quantum point contacts..................... 49 4.2.3. Gate setting............................ 50 5. Characteristics of a MZI 51 5.1.
    [Show full text]
  • Introduction to Quantum Field Theory
    Utrecht Lecture Notes Masters Program Theoretical Physics September 2006 INTRODUCTION TO QUANTUM FIELD THEORY by B. de Wit Institute for Theoretical Physics Utrecht University Contents 1 Introduction 4 2 Path integrals and quantum mechanics 5 3 The classical limit 10 4 Continuous systems 18 5 Field theory 23 6 Correlation functions 36 6.1 Harmonic oscillator correlation functions; operators . 37 6.2 Harmonic oscillator correlation functions; path integrals . 39 6.2.1 Evaluating G0 ............................... 41 6.2.2 The integral over qn ............................ 42 6.2.3 The integrals over q1 and q2 ....................... 43 6.3 Conclusion . 44 7 Euclidean Theory 46 8 Tunneling and instantons 55 8.1 The double-well potential . 57 8.2 The periodic potential . 66 9 Perturbation theory 71 10 More on Feynman diagrams 80 11 Fermionic harmonic oscillator states 87 12 Anticommuting c-numbers 90 13 Phase space with commuting and anticommuting coordinates and quanti- zation 96 14 Path integrals for fermions 108 15 Feynman diagrams for fermions 114 2 16 Regularization and renormalization 117 17 Further reading 127 3 1 Introduction Physical systems that involve an infinite number of degrees of freedom are usually described by some sort of field theory. Almost all systems in nature involve an extremely large number of degrees of freedom. A droplet of water contains of the order of 1026 molecules and while each water molecule can in many applications be described as a point particle, each molecule has itself a complicated structure which reveals itself at molecular length scales. To deal with this large number of degrees of freedom, which for all practical purposes is infinite, we often regard a system as continuous, in spite of the fact that, at certain distance scales, it is discrete.
    [Show full text]
  • Dirac Notation Frank Rioux
    Elements of Dirac Notation Frank Rioux In the early days of quantum theory, P. A. M. (Paul Adrian Maurice) Dirac created a powerful and concise formalism for it which is now referred to as Dirac notation or bra-ket (bracket ) notation. Two major mathematical traditions emerged in quantum mechanics: Heisenberg’s matrix mechanics and Schrödinger’s wave mechanics. These distinctly different computational approaches to quantum theory are formally equivalent, each with its particular strengths in certain applications. Heisenberg’s variation, as its name suggests, is based matrix and vector algebra, while Schrödinger’s approach requires integral and differential calculus. Dirac’s notation can be used in a first step in which the quantum mechanical calculation is described or set up. After this is done, one chooses either matrix or wave mechanics to complete the calculation, depending on which method is computationally the most expedient. Kets, Bras, and Bra-Ket Pairs In Dirac’s notation what is known is put in a ket, . So, for example, p expresses the fact that a particle has momentum p. It could also be more explicit: p = 2 , the particle has momentum equal to 2; x = 1.23 , the particle has position 1.23. Ψ represents a system in the state Q and is therefore called the state vector. The ket can also be interpreted as the initial state in some transition or event. The bra represents the final state or the language in which you wish to express the content of the ket . For example,x =Ψ.25 is the probability amplitude that a particle in state Q will be found at position x = .25.
    [Show full text]
  • Dirac Equation - Wikipedia
    Dirac equation - Wikipedia https://en.wikipedia.org/wiki/Dirac_equation Dirac equation From Wikipedia, the free encyclopedia In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it 1 describes all spin-2 massive particles such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity,[1] and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine details of the hydrogen spectrum in a completely rigorous way. The equation also implied the existence of a new form of matter, antimatter, previously unsuspected and unobserved and which was experimentally confirmed several years later. It also provided a theoretical justification for the introduction of several component wave functions in Pauli's phenomenological theory of spin; the wave functions in the Dirac theory are vectors of four complex numbers (known as bispinors), two of which resemble the Pauli wavefunction in the non-relativistic limit, in contrast to the Schrödinger equation which described wave functions of only one complex value. Moreover, in the limit of zero mass, the Dirac equation reduces to the Weyl equation. Although Dirac did not at first fully appreciate the importance of his results, the entailed explanation of spin as a consequence of the union of quantum mechanics and relativity—and the eventual discovery of the positron—represents one of the great triumphs of theoretical physics.
    [Show full text]
  • Quantum Droplets in Dipolar Ring-Shaped Bose-Einstein Condensates
    UNIVERSITY OF BELGRADE FACULTY OF PHYSICS MASTER THESIS Quantum Droplets in Dipolar Ring-shaped Bose-Einstein Condensates Author: Supervisor: Marija Šindik Dr. Antun Balaž September, 2020 UNIVERZITET U BEOGRADU FIZICKIˇ FAKULTET MASTER TEZA Kvantne kapljice u dipolnim prstenastim Boze-Ajnštajn kondenzatima Autor: Mentor: Marija Šindik Dr Antun Balaž Septembar, 2020. Acknowledgments I would like to express my sincerest gratitude to my advisor Dr. Antun Balaž, for his guidance, patience, useful suggestions and for the time and effort he invested in the making of this thesis. I would also like to thank my family and friends for the emotional support and encouragement. This thesis is written in the Scientific Computing Laboratory, Center for the Study of Complex Systems of the Institute of Physics Belgrade. Numerical simulations were run on the PARADOX supercomputing facility at the Scientific Computing Laboratory of the Institute of Physics Belgrade. iii Contents Chapter 1 – Introduction 1 Chapter 2 – Theoretical description of ultracold Bose gases 3 2.1 Contact interaction..............................4 2.2 The Gross-Pitaevskii equation........................5 2.3 Dipole-dipole interaction...........................8 2.4 Beyond-mean-field approximation......................9 2.5 Quantum droplets............................... 13 Chapter 3 – Numerical methods 15 3.1 Rescaling of the effective GP equation................... 15 3.2 Split-step Crank-Nicolson method...................... 17 3.3 Calculation of the ground state....................... 20 3.4 Calculation of relevant physical quantities................. 21 Chapter 4 – Results 24 4.1 System parameters.............................. 24 4.2 Ground state................................. 25 4.3 Droplet formation............................... 26 4.4 Critical strength of the contact interaction................. 28 4.5 The number of droplets...........................
    [Show full text]
  • Solitons and Quantum Behavior Abstract
    Solitons and Quantum Behavior Richard A. Pakula email: [email protected] April 9, 2017 Abstract In applied physics and in engineering intuitive understanding is a boost for creativity and almost a necessity for efficient product improvement. The existence of soliton solutions to the quantum equations in the presence of self-interactions allows us to draw an intuitive picture of quantum mechanics. The purpose of this work is to compile a collection of models, some of which are simple, some are obvious, some have already appeared in papers and even in textbooks, and some are new. However this is the first time they are presented (to our knowledge) in a common place attempting to provide an intuitive physical description for one of the basic particles in nature: the electron. The soliton model applied to the electrons can be extended to the electromagnetic field providing an unambiguous description for the photon. In so doing a clear image of quantum mechanics emerges, including quantum optics, QED and field quantization. To our belief this description is of highly pedagogical value. We start with a traditional description of the old quantum mechanics, first quantization and second quantization, showing the tendency to renounce to 'visualizability', as proposed by Heisenberg for the quantum theory. We describe an intuitive description of first and second quantization based on the concept of solitons, pioneered by the 'double solution' of de Broglie in 1927. Many aspects of first and second quantization are clarified and visualized intuitively, including the possible achievement of ergodicity by the so called ‘vacuum fluctuations’. PACS: 01.70.+w, +w, 03.65.Ge , 03.65.Pm, 03.65.Ta, 11.15.-q, 12.20.*, 14.60.Cd, 14.70.-e, 14.70.Bh, 14.70.Fm, 14.70.Hp, 14.80.Bn, 32.80.y, 42.50.Lc 1 Table of Contents Solitons and Quantum Behavior ............................................................................................................................................
    [Show full text]
  • Chapter 5 the Dirac Formalism and Hilbert Spaces
    Chapter 5 The Dirac Formalism and Hilbert Spaces In the last chapter we introduced quantum mechanics using wave functions defined in position space. We identified the Fourier transform of the wave function in position space as a wave function in the wave vector or momen­ tum space. Expectation values of operators that represent observables of the system can be computed using either representation of the wavefunc­ tion. Obviously, the physics must be independent whether represented in position or wave number space. P.A.M. Dirac was the first to introduce a representation-free notation for the quantum mechanical state of the system and operators representing physical observables. He realized that quantum mechanical expectation values could be rewritten. For example the expected value of the Hamiltonian can be expressed as ψ∗ (x) Hop ψ (x) dx = ψ Hop ψ , (5.1) h | | i Z = ψ ϕ , (5.2) h | i with ϕ = Hop ψ . (5.3) | i | i Here, ψ and ϕ are vectors in a Hilbert-Space, which is yet to be defined. For exampl| i e, c|omi plex functions of one variable, ψ(x), that are square inte­ 241 242 CHAPTER 5. THE DIRAC FORMALISM AND HILBERT SPACES grable, i.e. ψ∗ (x) ψ (x) dx < , (5.4) ∞ Z 2 formt heHilbert-Spaceofsquareintegrablefunctionsdenoteda s L. In Dirac notation this is ψ∗ (x) ψ (x) dx = ψ ψ . (5.5) h | i Z Orthogonality relations can be rewritten as ψ∗ (x) ψ (x) dx = ψ ψ = δmn. (5.6) m n h m| ni Z As see aboveexpressions look likeabrackethecalledthe vector ψn aket­ vector and ψ a bra-vector.
    [Show full text]
  • Second Quantization∗
    Second Quantization∗ Jörg Schmalian May 19, 2016 1 The harmonic oscillator: raising and lowering operators Lets first reanalyze the harmonic oscillator with potential m!2 V (x) = x2 (1) 2 where ! is the frequency of the oscillator. One of the numerous approaches we use to solve this problem is based on the following representation of the momentum and position operators: r x = ~ ay + a b 2m! b b r m ! p = i ~ ay − a : (2) b 2 b b From the canonical commutation relation [x;b pb] = i~ (3) follows y ba; ba = 1 y y [ba; ba] = ba ; ba = 0: (4) Inverting the above expression yields rm! i ba = xb + pb 2~ m! r y m! i ba = xb − pb (5) 2~ m! ∗Copyright Jörg Schmalian, 2016 1 y demonstrating that ba is indeed the operator adjoined to ba. We also defined the operator y Nb = ba ba (6) which is Hermitian and thus represents a physical observable. It holds m! i i Nb = xb − pb xb + pb 2~ m! m! m! 2 1 2 i = xb + pb − [p;b xb] 2~ 2m~! 2~ 2 2 1 pb m! 2 1 = + xb − : (7) ~! 2m 2 2 We therefore obtain 1 Hb = ! Nb + : (8) ~ 2 1 Since the eigenvalues of Hb are given as En = ~! n + 2 we conclude that the eigenvalues of the operator Nb are the integers n that determine the eigenstates of the harmonic oscillator. Nb jni = n jni : (9) y Using the above commutation relation ba; ba = 1 we were able to show that p a jni = n jn − 1i b p y ba jni = n + 1 jn + 1i (10) y The operator ba and ba raise and lower the quantum number (i.e.
    [Show full text]
  • Modeling Classical Dynamics and Quantum Effects In
    Modeling Classical Dynamics and Quantum Effects in Superconducting Circuit Systems by Peter Groszkowski A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Doctor of Philosophy in Physics Waterloo, Ontario, Canada, 2015 c Peter Groszkowski 2015 I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract In recent years, superconducting circuits have come to the forefront of certain areas of physics. They have shown to be particularly useful in research related to quantum computing and information, as well as fundamental physics. This is largely because they provide a very flexible way to implement complicated quantum systems that can be relatively easily manipulated and measured. In this thesis we look at three different applications where superconducting circuits play a central role, and explore their classical and quantum dynamics and behavior. The first part consists of studying the Casimir [20] and Casimir{Polder like [19] effects. These effects have been discovered in 1948 and show that under certain conditions, vacuum field fluctuations can mediate forces between neutral objects. In our work, we analyze analogous behavior in a superconducting system which consists of a stripline cavity with a DC{SQUID on one of its boundaries, as well as, in a Casimir{Polder case, a charge qubit coupled to the field of the cavity. Instead of a force, in the system considered here, we show that the Casimir and Casimir{ Polder like effects are mediated through a circulating current around the loop of the boundary DC{SQUID.
    [Show full text]