Encyclopedia of Scientific Principles, Laws, and Theories
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2016-2017 Year Book Www
1 2016-2017 YEAR BOOK WWW. C A R N E G I E S C I E N C E . E D U Department of Embryology 3520 San Martin Dr. / Baltimore, MD 21218 410.246.3001 Geophysical Laboratory 5251 Broad Branch Rd., N.W. / Washington, DC 20015-1305 202.478.8900 Department of Global Ecology 260 Panama St. / Stanford, CA 94305-4101 650.462.1047 The Carnegie Observatories 813 Santa Barbara St. / Pasadena, CA 91101-1292 626.577.1122 Las Campanas Observatory Casilla 601 / La Serena, Chile Department of Plant Biology 260 Panama St. / Stanford, CA 94305-4101 650.325.1521 Department of Terrestrial Magnetism 5241 Broad Branch Rd., N.W. / Washington, DC 20015-1305 202.478.8820 Office of Administration 1530 P St., N.W. / Washington, DC 20005-1910 202.387.6400 2 0 1 6 - 2 0 1 7 Y E A R B O O K The President’s Report July 1, 2016 - June 30, 2017 C A R N E G I E I N S T I T U T I O N F O R S C I E N C E Former Presidents Daniel C. Gilman, 1902–1904 Robert S. Woodward, 1904–1920 John C. Merriam, 1921–1938 Vannevar Bush, 1939–1955 Caryl P. Haskins, 1956–1971 Philip H. Abelson, 1971–1978 James D. Ebert, 1978–1987 Edward E. David, Jr. (Acting President, 1987–1988) Maxine F. Singer, 1988–2002 Michael E. Gellert (Acting President, Jan.–April 2003) Richard A. Meserve, 2003–2014 Former Trustees Philip H. Abelson, 1978–2004 Patrick E. -

Sequencing As a Way of Work
Edinburgh Research Explorer A new insight into Sanger’s development of sequencing Citation for published version: Garcia-Sancho, M 2010, 'A new insight into Sanger’s development of sequencing: From proteins to DNA, 1943-77', Journal of the History of Biology, vol. 43, no. 2, pp. 265-323. https://doi.org/10.1007/s10739-009- 9184-1 Digital Object Identifier (DOI): 10.1007/s10739-009-9184-1 Link: Link to publication record in Edinburgh Research Explorer Document Version: Peer reviewed version Published In: Journal of the History of Biology Publisher Rights Statement: © Garcia-Sancho, M. (2010). A new insight into Sanger’s development of sequencing: From proteins to DNA, 1943-77. Journal of the History of Biology, 43(2), 265-323. 10.1007/s10739-009-9184-1 General rights Copyright for the publications made accessible via the Edinburgh Research Explorer is retained by the author(s) and / or other copyright owners and it is a condition of accessing these publications that users recognise and abide by the legal requirements associated with these rights. Take down policy The University of Edinburgh has made every reasonable effort to ensure that Edinburgh Research Explorer content complies with UK legislation. If you believe that the public display of this file breaches copyright please contact [email protected] providing details, and we will remove access to the work immediately and investigate your claim. Download date: 28. Sep. 2021 THIS IS AN ADVANCED DRAFT OF A PUBLISHED PAPER. REFERENCES AND QUOTATIONS SHOULD ALWAYS BE MADE TO THE PUBLISHED VERION, WHICH CAN BE FOUND AT: García-Sancho M. -

Ira Sprague Bowen Papers, 1940-1973
http://oac.cdlib.org/findaid/ark:/13030/tf2p300278 No online items Inventory of the Ira Sprague Bowen Papers, 1940-1973 Processed by Ronald S. Brashear; machine-readable finding aid created by Gabriela A. Montoya Manuscripts Department The Huntington Library 1151 Oxford Road San Marino, California 91108 Phone: (626) 405-2203 Fax: (626) 449-5720 Email: [email protected] URL: http://www.huntington.org/huntingtonlibrary.aspx?id=554 © 1998 The Huntington Library. All rights reserved. Observatories of the Carnegie Institution of Washington Collection Inventory of the Ira Sprague 1 Bowen Papers, 1940-1973 Observatories of the Carnegie Institution of Washington Collection Inventory of the Ira Sprague Bowen Paper, 1940-1973 The Huntington Library San Marino, California Contact Information Manuscripts Department The Huntington Library 1151 Oxford Road San Marino, California 91108 Phone: (626) 405-2203 Fax: (626) 449-5720 Email: [email protected] URL: http://www.huntington.org/huntingtonlibrary.aspx?id=554 Processed by: Ronald S. Brashear Encoded by: Gabriela A. Montoya © 1998 The Huntington Library. All rights reserved. Descriptive Summary Title: Ira Sprague Bowen Papers, Date (inclusive): 1940-1973 Creator: Bowen, Ira Sprague Extent: Approximately 29,000 pieces in 88 boxes Repository: The Huntington Library San Marino, California 91108 Language: English. Provenance Placed on permanent deposit in the Huntington Library by the Observatories of the Carnegie Institution of Washington Collection. This was done in 1989 as part of a letter of agreement (dated November 5, 1987) between the Huntington and the Carnegie Observatories. The papers have yet to be officially accessioned. Cataloging of the papers was completed in 1989 prior to their transfer to the Huntington. -

Early Synchrotrons in Britain, and Early Work for Cern
EARLY SYNCHROTRONS IN BRITAIN, AND EARLY WORK FOR CERN J. D. Lawson Formerly Rutherford Appleton Laboratory, Chilton, Oxon, UK Abstract Early work on electron synchrotrons in the UK, including an account of the conversion of a small betatron in 1946 to become the world’s first synchrotron, is described first. This is followed by a description of the design and construction of the 1 GeV synchrotron at the University of Birmingham which was started in the same year. Finally an account is given of the work of the international team during 1952–3, which formed the basis for the design of the CERN PS before the move to Geneva. It was during this year that John Adams showed the outstanding ability that later brought the project to such a successful conclusion. 1 EARLY PLANS IN BRITAIN: THE WORLD’S FIRST SYNCHROTRON During the second world war Britain’s nuclear physicists were deployed in research directed towards winning the war. Many were engaged in developments associated with radar, (or ‘radiolocation’ as it was then called), both at universities and at government laboratories, such as the radar establishments TRE and ADRDE at Malvern. Others contributed to the atomic bomb programme, both in the UK, and in the USA. Towards the end of the war, when victory seemed assured, the nuclear physicists began looking towards the peacetime future. The construction of new particle accelerators to achieve ever higher energies was seen as one of the more important possibilities. Those working at Berkeley on the electromagnetic separator were familiar with the accelerators there, and following the independent invention (or discovery?) there of the principle of phase stability by Edwin McMillan in 1945, exciting possibilities were immediately apparent [4]. -

Glossary Glossary
Glossary Glossary Albedo A measure of an object’s reflectivity. A pure white reflecting surface has an albedo of 1.0 (100%). A pitch-black, nonreflecting surface has an albedo of 0.0. The Moon is a fairly dark object with a combined albedo of 0.07 (reflecting 7% of the sunlight that falls upon it). The albedo range of the lunar maria is between 0.05 and 0.08. The brighter highlands have an albedo range from 0.09 to 0.15. Anorthosite Rocks rich in the mineral feldspar, making up much of the Moon’s bright highland regions. Aperture The diameter of a telescope’s objective lens or primary mirror. Apogee The point in the Moon’s orbit where it is furthest from the Earth. At apogee, the Moon can reach a maximum distance of 406,700 km from the Earth. Apollo The manned lunar program of the United States. Between July 1969 and December 1972, six Apollo missions landed on the Moon, allowing a total of 12 astronauts to explore its surface. Asteroid A minor planet. A large solid body of rock in orbit around the Sun. Banded crater A crater that displays dusky linear tracts on its inner walls and/or floor. 250 Basalt A dark, fine-grained volcanic rock, low in silicon, with a low viscosity. Basaltic material fills many of the Moon’s major basins, especially on the near side. Glossary Basin A very large circular impact structure (usually comprising multiple concentric rings) that usually displays some degree of flooding with lava. The largest and most conspicuous lava- flooded basins on the Moon are found on the near side, and most are filled to their outer edges with mare basalts. -

Cambridge's 92 Nobel Prize Winners Part 2 - 1951 to 1974: from Crick and Watson to Dorothy Hodgkin
Cambridge's 92 Nobel Prize winners part 2 - 1951 to 1974: from Crick and Watson to Dorothy Hodgkin By Cambridge News | Posted: January 18, 2016 By Adam Care The News has been rounding up all of Cambridge's 92 Nobel Laureates, celebrating over 100 years of scientific and social innovation. ADVERTISING In this installment we move from 1951 to 1974, a period which saw a host of dramatic breakthroughs, in biology, atomic science, the discovery of pulsars and theories of global trade. It's also a period which saw The Eagle pub come to national prominence and the appearance of the first female name in Cambridge University's long Nobel history. The Gender Pay Gap Sale! Shop Online to get 13.9% off From 8 - 11 March, get 13.9% off 1,000s of items, it highlights the pay gap between men & women in the UK. Shop the Gender Pay Gap Sale – now. Promoted by Oxfam 1. 1951 Ernest Walton, Trinity College: Nobel Prize in Physics, for using accelerated particles to study atomic nuclei 2. 1951 John Cockcroft, St John's / Churchill Colleges: Nobel Prize in Physics, for using accelerated particles to study atomic nuclei Walton and Cockcroft shared the 1951 physics prize after they famously 'split the atom' in Cambridge 1932, ushering in the nuclear age with their particle accelerator, the Cockcroft-Walton generator. In later years Walton returned to his native Ireland, as a fellow of Trinity College Dublin, while in 1951 Cockcroft became the first master of Churchill College, where he died 16 years later. 3. 1952 Archer Martin, Peterhouse: Nobel Prize in Chemistry, for developing partition chromatography 4. -

A Scientific Jackpot: the Nobel Prize for Penn Trio a Gentleman Dr
See the back page UNIVERSITY of PENNSYLVANIA for more Tuesday, on the October 17, 2000 Nobel Laureate, Volume 47 Number 8 Alan MacDiarmid. www.upenn.edu/almanac/ Toasting A Chemist and A Scientific Jackpot: The Nobel Prize for Penn Trio A Gentleman Dr. Alan G. MacDiarmid, structure. For a polymer to conduct electric current, it must “A Penn Nobel Blanchard Professor of Chem- consist alternately of single and double bonds between the Prize,”... “based on istry, is one of three recipients carbon atoms. It must also be “doped,” which means that great applied and of the 2000 Nobel Prize in electrons are removed (through oxidation) or introduced basic science,” is Chemistry. Sharing the honor (through reduction). These “holes,” or extra electrons, can how Roy Vagelos are former Penn professor Dr. move along the molecule, making it electrically conductive. described the accom- Alan J. Heeger, now at the Uni- Drs. MacDiarmid, Heeger, and Shirakawa were respon- plishment of “one of versity of California at Santa sible for the 1977 synthesis and the electrical and chemical our best teachers and Barbara, and Dr. Hideki doping of polyacetylene, the prototypical conducting poly- researchers.” Shirakawa, of the University of mer, and the rediscovery of polyaniline, now the foremost Tsukuba in Japan. industrial conducting polymer. They have subsequently de- “It’s an understate- The work underlying the veloped conductive polymers into a research field of great ment that we’ve award—which showed that importance for chemists as well as physicists. The area has been waiting for this plastics can be made to conduct also yielded important practical applications. -

Effect of Target Properties on the Impact Cratering Process
WORKSHOP PROGRAM AND ABSTRACTS LPI Contribution No. 1360 BRIDGING THE GAP II: EFFECT OF TARGET PROPERTIES ON THE IMPACT CRATERING PROCESS September 22–26, 2007 Saint-Hubert, Canada SPONSORS Canadian Space Agency Lunar and Planetary Institute Barringer Crater Company NASA Planetary Geology and Geophysics Program CONVENERS Robert Herrick, University of Alaska Fairbanks Gordon Osinski, Canadian Space Agency Elisabetta Pierazzo, Planetary Science Institute SCIENTIFIC ORGANIZING COMMITTEE Mark Burchell, University of Kent Gareth Collins, Imperial College London Michael Dence, Canadian Academy of Science Kevin Housen, Boeing Corporation Jay Melosh, University of Arizona John Spray, University of New Brunswick Lunar and Planetary Institute 3600 Bay Area Boulevard Houston TX 77058-1113 LPI Contribution No. 1360 Compiled in 2007 by LUNAR AND PLANETARY INSTITUTE The Institute is operated by the Universities Space Research Association under Agreement No. NCC5-679 issued through the Solar System Exploration Division of the National Aeronautics and Space Administration. Any opinions, findings, and conclusions or recommendations expressed in this volume are those of the author(s) and do not necessarily reflect the views of the National Aeronautics and Space Administration. Material in this volume may be copied without restraint for library, abstract service, education, or personal research purposes; however, republication of any paper or portion thereof requires the written permission of the authors as well as the appropriate acknowledgment of this publication. Abstracts in this volume may be cited as Author A. B. (2007) Title of abstract. In Bridging the Gap II: Effect of Target Properties on the Impact Cratering Process, p. XX. LPI Contribution No. 1360, Lunar and Planetary Institute, Houston. -

12TH ASIAN CHEMICAL CONGRESS (12ACC) 2007 Registration Form
No. 1 / 2007 ■ Kuwait Chemical Society Symposium on Application of Catalyst in the Industry ■ 2006 Activities and 2007 President Profiles of the Member Societies www.facs-as.org Federation of Asian Chemical Societies Newsletter | No. 1 / 2007 ontents Obituary ■ Dr. Tan Sri B C Sekhar (1929 – 2006) 4 ■ Prof. Hitoshi Ohtaki (1932 – 2006) 6 Special Symposium ■ Kuwait Chemical Society Symposium on Application of Catalyst in the Industry (Fuel, Pollution and Drugs) 9 Biofuels: Emerging Renewable Energy for the Transportation Sector 10 Discrete Physico-Chemical Processes that Characterise Water Pollution 13 Peptide-Cleaving Catalyst as a New Paradigm in Drug Discovery 16 2006 Activities and 2007 President Profiles of the Member Societies ■ Brunei Darussalam Institute of Chemistry 18 ■ Chinese Chemical Society 20 ■ Hong Kong Chemical Society 22 ■ Institut Kimia Malaysia 23 ■ Korean Chemical Society 27 ■ New Zealand Institute of Chemistry 29 ■ Royal Australian Chemical Institute 32 FACS Activities ■ Minutes of the 49th EXCO Meeting 34 ■ FACS Project Reports Asian Chemicla Education Network (ACEN) 41 Asian Network for Environmental chemistry (ANEC) 42 Low-Cost Instrumentation-Microscale Chemistry (LCI-MSC) 47 Meeting Announcement: The 12th Asian Chemical Congress 49 Directories ■ FACS EXCO Members (2005-2007) 55 ■ Member Societies 56 ■ Project Directors (2006-2007) 58 ■ FACS Fellows 59 ■ FACS Life-time Members 60 An electronic version of FACS Newsletter is available at http://www.facs.org. Obituary The Late Academician Dr. Tan Sri B C Sekhar (1929 – 2006) he Late academician Dr. Tan Sri B C Sekhar, born on November 17, 1929 at Sungai Buloh, Malaysia near the 3,400-acre experiment station of the Rubber Research Institute of Malaysia (RRIM), was fondly known as Mr Natural Rubber for his motivation, passion and commitment to the development of natural rubber industry. -

MASTER NATIONAL ACADEMY PRESS Washington, D.C 1983
OPPORTUNITIES AND CHALLENGES IN C0NP 830214 RESEARCH WITH TRANSPLUTONIUM ELEMENTS DE85 010852 Board on Chemical Sciences and Technology Committee on Nuclear and Radlochemistry Commission on Physical Sciences, Mathematics, and Resources National Research Council DISCLAIMER This iw.oort was prepared as an account of work spcnsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsi- bility for the accuracy, completeness, or usefulness of any infonnation, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Refer- ence herein to any specific commercial product, process, or scivice by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recom- mendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. MASTER NATIONAL ACADEMY PRESS Washington, D.C 1983 DISTBIBUHOU OF THIS DOCUMENT IS Workshop Steering Committee Gerhart Friedlander, Brookhaven National Laboratory, Chairman Gregory R. Choppin, Florida State University Richard L. Hoff, Lawrence Livermore National Laboratory Darleane C. Hoffman, Los Alamos Scientific Laboratory, Ex-Officio James A. Ibers, Northwestern University Robert A. Penneman, Los Alamos Scientific Laboratory Thomas G. Spiro, Princeton University Henry Taube, Stanford University Joseph Weneser, Brookhaven National Laboratory Raymond G. Wymer, Oak Ridge National Laboratory, Ex-Officio NRC Staff William Spindel, Executive Secretary Peggy J. Posey, Staff Associate Robert M. -

Naval Juniorreserve ()Hiders
DOCUMENT RESUME ED 219 280 SE 038 787 e $ . AUTHOR ' Omans, S. E.; And Others TITLE Workbook for Naval Science 3: An Illustrated Workbook for the NJROTC Sjudent. Focus. on the Trained Person. Technical Report 124. INSTITUTION University of Central Florida, Orlando.. -, SPONS AGENCY Naval %Training Analysis and Evaluation Group, Orlando, Fla. PUB DATE May f2 GRANT N61339-79-D-0105 4 NOTE if 348p.- 4 ,EDRS PRICE MF01/PC14 Plus Postage. DESCRIPTORS Astronomy; Electricity; High Schools; Instructional -Materials; *Leadership; Meteotiology; Military Science; *Military Training; *Physical Sciences; ( *Remedial Reading; *Secondary School Science; Workbooks' _ IDENTIFIERS Navaleistory; *Naval JuniorReserve ()Hiders . ,-..\ Traiffing torps , '-'--..... ..,. ABSTRACT This workbook (first in a series of three) - supplements the textbook of the third year Naval Junior Reserve Officers Training Corps (NJROTC),program and is designed for NJROTC students who do not have the reading skillsOlecessary to fully benefit from the regular curriculum materidls. The workbook is written at the eighth-grade readability level as detprmined by a Computer Readability Editing System'analysis. In addition to its use in the NJROTC program, the wdrkbook may be useful in 'several remedial programs such as Academic Remedial Training(ART) and;the Verbal' Skills Curriculum,\Jzoth of which are offered at each 'of the three . RecruitTraining Com?nands to recruits deficient in reading or oral English skills.' Topics' in the workbook include naval history (1920-1945), leadership.characteristiCs, meteorology, astronomy, sand introductory electricity.'Exercises-include'vocabulary development, matching, concept application, and -extending Yearning actrties. (Author/JN) V 1' ****************************.0***,*************************************** * * Reproductions suppled'bi EDRS are the best that can be made. from- the oryiginal% document. -
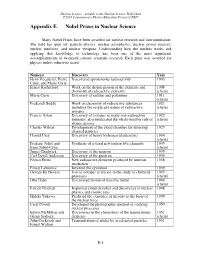
Appendix E Nobel Prizes in Nuclear Science
Nuclear Science—A Guide to the Nuclear Science Wall Chart ©2018 Contemporary Physics Education Project (CPEP) Appendix E Nobel Prizes in Nuclear Science Many Nobel Prizes have been awarded for nuclear research and instrumentation. The field has spun off: particle physics, nuclear astrophysics, nuclear power reactors, nuclear medicine, and nuclear weapons. Understanding how the nucleus works and applying that knowledge to technology has been one of the most significant accomplishments of twentieth century scientific research. Each prize was awarded for physics unless otherwise noted. Name(s) Discovery Year Henri Becquerel, Pierre Discovered spontaneous radioactivity 1903 Curie, and Marie Curie Ernest Rutherford Work on the disintegration of the elements and 1908 chemistry of radioactive elements (chem) Marie Curie Discovery of radium and polonium 1911 (chem) Frederick Soddy Work on chemistry of radioactive substances 1921 including the origin and nature of radioactive (chem) isotopes Francis Aston Discovery of isotopes in many non-radioactive 1922 elements, also enunciated the whole-number rule of (chem) atomic masses Charles Wilson Development of the cloud chamber for detecting 1927 charged particles Harold Urey Discovery of heavy hydrogen (deuterium) 1934 (chem) Frederic Joliot and Synthesis of several new radioactive elements 1935 Irene Joliot-Curie (chem) James Chadwick Discovery of the neutron 1935 Carl David Anderson Discovery of the positron 1936 Enrico Fermi New radioactive elements produced by neutron 1938 irradiation Ernest Lawrence