DOCSLIB.ORG

Task Related Sensorimotor Adjustments Increase the Sensory Range in Electrolocation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Task Related Sensorimotor Adjustments Increase the Sensory Range in Electrolocation Research Articles: Behavioral/Cognitive Task related sensorimotor adjustments increase the sensory range in electrolocation https://doi.org/10.1523/JNEUROSCI.1024-19.2019 Cite as: J. Neurosci 2019; 10.1523/JNEUROSCI.1024-19.2019 Received: 14 May 2019 Revised: 9 November 2019 Accepted: 18 November 2019 This Early Release article has been peer-reviewed and accepted, but has not been through the composition and copyediting processes. The final version may differ slightly in style or formatting and will contain links to any extended data. Alerts: Sign up at www.jneurosci.org/alerts to receive customized email alerts when the fully formatted version of this article is published. Copyright © 2019 the authors Title: Task related sensorimotor adjustments increase the sensory range in electrolocation Abbreviated title: Sensorimotor learning improves the sensory range Authors: Federico Pedraja1, Volker Hofmann1,2, Julie Goulet1, Jacob Engelmann1* Affiliations: 1 Bielefeld University, Faculty of Biology/CITEC, AG Active Sensing, Postfach 100131, D-33501 Biele- feld, GERMANY 2 McGill University, Department of Physiology, 3655 Promenade Sir William Osler, Montreal, QC, H3G 1Y6 CANADA * Corresponding author: Jacob Engelmann AG Active Sensing Bielefeld University D-33501 Bielefeld, Germany Tel +49-521-106-4641 [email protected] Number of pages: 38 Number of figures: 9 Number of words: abstract (163 words), introduction (556 words), discussion (1609 words). Competing interests: Authors of this manuscript do not have any financial or non-financial compet- ing interests. Acknowledgments: This work was supported by the Cluster of Excellence Cognitive Interaction Tech- nology ‘CITEC’ (EXC 277) and the DFG (EN 826/5-1). ABSTRACT 1 Perception and motor control traditionally are studied separately. However, motor activity can serve 2 as a scaffold to shape the sensory flow. This tight link between motor actions and sensing is particu- 3 larly evident in active sensory systems. Here, we investigate how the weakly electric mormyrid fish 4 Gnathonemus petersii of undetermined sex structure their sensing and motor behavior while learn- 5 ing a perceptual task. We find systematic adjustments of the motor behavior that correlate with an 6 increased performance. Using a model to compute the electrosensory input, we show that these 7 behavioural adjustments improve the sensory input. As we find low neuronal detection thresholds at 8 the level of medullary electrosensory neurons, it seems that the behavior-driven improvements of 9 the sensory input are highly suitable to overcome the sensory limitations, thereby increasing the 10 sensory range. Our results show that motor control is an active component of sensory learning, 11 demonstrating that a detailed understanding of contribution of motor actions to sensing is needed to 12 understand even seemingly simple behaviors. 1 13 SIGNIFICANCE STATEMENT 14 Motor-guided sensation and perception are intertwined, with motor behavior serving as a scaffold to 15 shape the sensory input. We characterized how the weakly electric mormyrid fish G. petersii, as it 16 learns a perceptual task, restructures its sensorimotor behavior. We find that systematic adjustments 17 of the motor behavior correlate with increased performance and a shift of the animal’s sensory at- 18 tention. Analyzing the afferent electrosensory input shows that a significant gain in information re- 19 sults from these sensorimotor adjustments. Our results show that motor control can be an active 20 component of sensory learning. Researching the sensory corollaries of motor control thus can be 21 crucial to understand sensory sensation and perception under naturalistic conditions. 2 INTRODUCTION 22 Exploratory behavior is a crucial substrate for learning (Loewenstein, 1994). As the animals’ move- 23 ments influence the sensory input, re-organizing the motor patterns with respect to recent experi- 24 ence may contribute to learning thereby improving behavior. Analyzing these modifications can thus 25 reveal how motor action contributes to learning (Wolpert and Landy, 2012; O’Hora et al., 2013) and 26 aid decision making through action selection (Charlesworth et al., 2011; O’Hora et al., 2013; 27 Zgonnikov et al., 2017). 28 While the variability of motor behavior may facilitate motor learning by widening the search space 29 from which behaviors are instantiated (Brainard and Doupe, 2013; Wu et al., 2014), the same varia- 30 bility can set bounds on the task-optimization of motor control (van Beers et al., 2002). This is partic- 31 ularly evident in active sensory systems, where the sensory input directly depends on the motor out- 32 put. Here the strong sensorimotor dependencies may be exploited by an animal to adjust motor be- 33 havior in order to not only improve the motor but also the sensing efficiency (Friston, 2010; Little and 34 Sommer, 2013; Gordon et al., 2014). 35 36 We here investigated how sensorimotor behavior changes while Gnathonemus petersii, a pulse type 37 weakly electric fish, learned a detection task. During active electrolocation these fish obtain sensory 38 information through brief discharges of a specialized electric organ in their tail (electric organ dis- 39 charge, EOD). The discharge rate is under top-down control and changes in a context-dependent 40 manner (Post and von der Emde, 1999; Caputi et al., 2003). Each emitted EOD creates a 3- 41 dimensional electric field around the fish which is perturbed by nearby objects (Lissmann and 42 Machin, 1958). Also motion of the animal can perturb the electric field (e.g., tail movement (Sawtell 43 et al., 2006)), both of which are perceived by electroreceptors in the skin of the fish. To discriminate 44 between the predictable (re-afferent) and unpredictable (ex-afferent) components of the sensory 45 input, weakly electric fish are known to rely on a sophisticated neuronal circuitry (Sawtell et al., 46 2005; Bell et al., 2008) which enables them to analyze their nearby environment. 47 Not all (re-afferent) sensory consequences of behavior must be unfavorable however: Similar to oth- 48 er organisms (Poteser and Kral, 1995; Kern et al., 2001), weakly electric fish exhibit a variety of stere- 49 otyped behaviors (Toerring and Belbenoit, 1979; Toerring and Moller, 1984; Nelson and Maciver, 50 1999; Hofmann et al., 2014). Recent studies have revealed that behaviorally relevant sensory infor- 51 mation can emerge from such strongly patterned sensorimotor behaviors, i.e. weakly electric fish 52 actively exploit these sensorimotor dependencies (Hofmann et al., 2017; Pedraja et al., 2018). 3 53 The ability to control the timing of sensory sampling while at the same time being able to shape the 54 properties of the sensory input through their motor behavior makes weakly electric fish particularly 55 suitable to study how changes in exploratory behaviors can guide sensory-driven learning efficiently. 56 We here focussed on a reinforced object detection task and found that performance was progres- 57 sively enhanced by consistent changes of the motor patterns. These changes resulted in an increased 58 sensory range. Our results add further support to the idea that weakly electric fish actively improve 59 sensing capabilities by selecting purposeful components from their motor repertoire and focus their 60 electric attention in a goal-directed manner. Such behavioral control of the sensory input might con- 61 tribute to improving neuronal stimulus detection and encoding, as we found neuronal performance 62 to be relatively poor at the level of the medulla. 63 4 64 MATERIAL AND METHODS 65 Animals. Wild-caught Gnathonemus petersii of either sex were obtained from a commercial fish 66 dealer (Aquarium Glaser, Rodgau, Germany) and housed in communal 400L aquaria. The water tem- 67 perature in these aquaria and the set-up was 25 ± 1 °C at a conductivity of 100 ± 5 μS cm−1 and a 68 12L:12D photoperiod. Fish were fed with bloodworms. All procedures for animal maintenance and 69 preparations comply with the current animal protection law of the Federal Republic of Germany and 70 have been approved by the local authorities (Landesamt für Natur, Umwelt und Verbraucherschutz 71 Nordrhein-Westfalen: 87–51- 04.2010.A202). 72 Behavior 73 Training setup. Five G. petersii (length of 11 ± 1 cm) housed in separate experimental tanks and fed 74 with bloodworms to satiation three times per week before the beginning of the behavioral experi- 75 ment. The experimental tanks (120 · 50 · 50 cm) were divided in a living area (60 · 50 cm; 30 cm, wa- 76 ter level) that was separated by a plastic gate from the experimental area (60 · 50 cm; 10 cm, water 77 level). The floor in the experimental area was 20 cm above the floor of the living area, which con- 78 fined the movements of the animal in the experimental area into two dimensions. A plastic plate 79 divided the proximal end (20 cm) of the experimental arena in two compartments. Perpendicular to 80 this plate a 1 cm wide plastic strip marked the entry to the compartments on the floor. A metal cube 81 (2 · 2 · 2 cm) was placed on the floor at the decision line, centered in front of the cued compartment 82 where it served as a cue to the rewarded compartment (S+). Experiments were performed in dark- 83 ness (< 0.1 lux measured above the water level) and videotaped from the top (60 fps; AVT Marlin F- 84 131 & F-033) using IR-illumination (880 nm) from below. This wavelength is beyond the perceptual 85 range of this species (Ciali et al., 1997). EODs were recorded differentially (custom-built electrode 86 array, 0.6 – 40 kHz band pass) and stored as events (PC audio card, 12 bit, 10 kHz) alongside acquired 87 videos. 88 Experimental design, video tracking and statistical analysis. Animals first learned to swim through 89 the opened gate to the proximal end of the arena to receive food. Once fish did this reliably training 90 commenced, and videos of each trial were acquired.
Load more

Recommended publications
  • M.A. Maciver's Dissertation
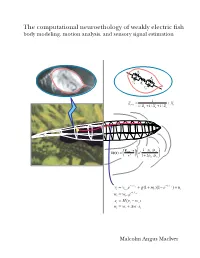
    The computational neuroethology of weakly electric fish body modeling, motion analysis, and sensory signal estimation R s R s C R s i C s 1 Z = + X prey + + s 1/ Rp 1/ Xp 1/ Zs −ρ ρ E ⋅r 1 p / w δφ(r) = fish a3 3 + ρ ρ r 1 2 p / w − t − t = 1/ v + + − 1/ v + vt vt−1e g(1 mt )(1 e ) nt − t = 1/ w wt wt−1e = − st H(vt wt ) = + ∆ ⋅ wt wt w st Malcolm Angus MacIver THE COMPUTATIONAL NEUROETHOLOGY OF WEAKLY ELECTRIC FISH: BODY MODELING, MOTION ANALYSIS, AND SENSORY SIGNAL ESTIMATION BY MALCOLM ANGUS MACIVER B.Sc., University of Toronto, 1991 M.A., University of Toronto, 1992 THESIS Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Neuroscience in the Graduate College of the University of Illinois at Urbana-Champaign, 2001 Urbana, Illinois c Copyright by Malcolm Angus MacIver, 2001 ABSTRACT Animals actively influence the content and quality of sensory information they acquire through the positioning of peripheral sensory surfaces. Investigation of how the body and brain work together for sensory acquisition is hindered by 1) the limited number of techniques for tracking sensory surfaces, few of which provide data on the position of the entire body surface, and by 2) our inability to measure the thousands of sensory afferents stimulated during behav- ior. I present research on sensory acquisition in weakly electric fish of the genus Apteronotus, where I overcame the first barrier by developing a markerless tracking system and have de- ployed a computational approach toward overcoming the second barrier.
    [Show full text]
  • The Evolution of Echolocation for Predation
    Symp. zool. Soc. Land. (1993) No. 65: 39-63 The evolution of echolocation for predation J. R. SPEAKMAN DepartmentofZoowgy University of Aberdeen Aberdeen AB9 2TN, UK Synopsis Active detection of food items by echolocation has some obvious advantages over passive detection, since it affords independence from ambient light and sound levels. For predatory animals, however, echolocation would also appear to have a significant disadvanrage-i-the echolocation calls might alert prey to the predator's presence. Surprisingly, therefore, all but two of the different groups of vertebrates that have evolved echolocation are predatory. Despite the diversity of predatory taxa in which echolocation has evolved it is still a relatively uncommon form of perception. It has been suggested that a major constraint on the evolution of echolocation is its high energy cost, due to rapid attenuation of sound in air. The cost of producing echolocation calls has been measured in insectivorous bats, whilst hanging at rest. These measures confirm that echolocation is extremely costly. However, bats normally echolocate in flight which also has a high cost. How bats cope with the high cost of echolocation, when it is combined with flight, is therefore of extreme interest. Measures of the energy cost of flight of small echolocating bats ggest that the cost is no greater than that for non-echolocating birds and bats. The son for this apparent economy is that the same muscles which flap the wings also tilate the lungs, and produce the pulse of breath which generates the echolocation For a bat in flight, therefore, the additional cost of echolocating is very low, sr for a bat on the ground, and presumably other terrestrial vertebrates, the cost ry high.
    [Show full text]
  • Evidence for Mutual Allocation of Social Attention Through Interactive Signaling in a Mormyrid Weakly Electric Fish
    Evidence for mutual allocation of social attention through interactive signaling in a mormyrid weakly electric fish Martin Worma,1, Tim Landgrafb, Julia Prumea, Hai Nguyenb, Frank Kirschbaumc, and Gerhard von der Emdea aInstitut für Zoologie, Neuroethologie/Sensorische Ökologie, Universität Bonn, 53115 Bonn, Germany; bInstitut für Informatik, Fachbereich Informatik und Mathematik, Freie Universität Berlin, 14195 Berlin, Germany; and cBiologie und Ökologie der Fische, Lebenswissenschaftliche Fakultät, Humboldt-Universität-zu Berlin, 10115 Berlin, Germany Edited by John G. Hildebrand, University of Arizona, Tucson, AZ, and approved May 16, 2018 (received for review January 26, 2018) Mormyrid weakly electric fish produce electric organ discharges responses from a conspecific. We solved both problems by using (EODs) for active electrolocation and electrocommunication. These a freely moving robotic fish capable of emitting either predefined pulses are emitted with variable interdischarge intervals (IDIs) or dynamic sequences of playback EODs in an interactive be- resulting in temporal discharge patterns and interactive signaling havioral experiment with single individuals of the weakly electric episodes with nearby conspecifics. However, unequivocal assign- fish Mormyrus rume proboscirostris. ment of interactive signaling to a specific behavioral context has Robotic fish have been successfully employed to investigate the proven to be challenging. Using an ethorobotical approach, we features determining attraction between individual fish (14–16), as confronted single individuals of weakly electric Mormyrus rume well as collective decision making and internal dynamics in groups – proboscirostris with a mobile fish robot capable of interacting of fish in shoals (17 22). Similar experiments have demonstrated both physically, on arbitrary trajectories, as well as electrically, that mormyrids are attracted to a mobile fish replica playing back by generating echo responses through playback of species- electric signals (23, 24).
    [Show full text]
  • Tony J. Prescott Ehud Ahissar Eugene Izhikevich Editors Scholarpedia of Touch Scholarpedia
    Scholarpedia Series Editor: Eugene Izhikevich Tony J. Prescott Ehud Ahissar Eugene Izhikevich Editors Scholarpedia of Touch Scholarpedia Series editor Eugene Izhikevich, San Diego, USA [email protected] More information about this series at http://www.springer.com/series/13574 [email protected] Tony J. Prescott • Ehud Ahissar Eugene Izhikevich Editors Scholarpedia of Touch [email protected] Editors Tony J. Prescott Eugene Izhikevich Department of Psychology Brain Corporation University of Sheffield San Diego, CA Sheffield USA UK Ehud Ahissar Department of Neurobiology Weizmann Institute of Science Rehovot Israel Scholarpedia ISBN 978-94-6239-132-1 ISBN 978-94-6239-133-8 (eBook) DOI 10.2991/978-94-6239-133-8 Library of Congress Control Number: 2015948155 © Atlantis Press and the author(s) 2016 This book, or any parts thereof, may not be reproduced for commercial purposes in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system known or to be invented, without prior permission from the Publisher. Printed on acid-free paper [email protected] Preface Touch is the ability to understand the world through physical contact. The noun “touch” and the verb “to touch” derive from the Old French verb “tochier”. Touch perception is also described by the adjectives tactile, from the Latin “tactilis”, and haptic, from the Greek “haptόs”. Academic research concerned with touch is also often described as haptics. The aim of Scholarpedia of Touch, first published by Scholarpedia (www. scholarpedia.org), is to provide a comprehensive set of articles, written by leading researchers and peer reviewed by fellow scientists, detailing the current scientific understanding of the sense of touch and of its neural substrates in animals including humans.
    [Show full text]
  • Making Sense: Weakly Electric Fish Modulate Sensory Feedback
    MAKING SENSE: WEAKLY ELECTRIC FISH MODULATE SENSORY FEEDBACK VIA SOCIAL BEHAVIOR AND MOVEMENT by Sarah A. Stamper A dissertation submitted to Johns Hopkins University in conformity with the requirements for the degree of Doctor of Philosophy Baltimore, Maryland June, 2012 © 2012 Sarah Stamper All Rights Reserved Abstract Animals rely on sensory information for the control of their behavior. Understanding this process requires a detailed description of the sensory feedback that they receive, which is often determined by an animal’s proximity to conspecifics and its own movement within the environment. This dissertation examines the role of social behavior and movement for the modulation of electrosensory feedback in weakly electric fish. We made observations of weakly electric fish in their natural habitats and found that some species of fish, which typically have more complex social behaviors, are most often found in groups. These same species will preferentially approach a refuge with a social signal in the laboratory. As a result of social grouping these fish receive continuous electrosensory oscillations (amplitude and phase modulations) caused by the interactions from the electric fields of each individual. Interestingly, both social grouping and movement can produce higher order modulations (termed ‘envelopes’), which can have lower frequency content than the first order modulations. Curiously, we did not observe low frequency envelopes in the majority of our samples. To determine why that might be the case we tested the behavioral responses of weakly electric fish to envelope stimuli in controlled laboratory experiments. We found that Eigenmannia will increase or decrease their electric organ discharge (EOD) frequency in response to social envelope stimuli, termed the Social Envelope Response (SER).
    [Show full text]
  • Springer Handbook of Auditory Research
    Springer Handbook of Auditory Research Series Editors: Richard R. Fay and Arthur N. Popper Theodore H. Bullock Carl D. Hopkins Arthur N. Popper Richard R. Fay Editors Electroreception With 118 illustrations and two color illustrations Theodore H. Bullock Carl D. Hopkins Department of Neurosciences Department of Neurobiology & Behavior School of Medicine Cornell University University of California, San Diego Ithaca, NY 14583, USA La Jolla, CA 92093-0240, USA [email protected] [email protected] Arthur N. Popper Richard R. Fay Department of Biology Parmly Hearing Institute and Department University of Maryland of Psychology College Park, MD 20742, USA Loyola University of Chicago [email protected] Chicago, IL 60626, USA [email protected] Cover illustration: Gymnotiform fishes from South America utilize electroreception for passive sensing of prey, for active sensing objects detected as distortions in their own electric fields, and for sensing electric communication signals generated from their electric organs. A few of the 27 known genera of gymnotiforms are illustrated: Electrophorus, Gymnotus, Microsternarchus, Brachyhypopomus, Hypopomus, Racenisia, Hypopygus, Steatogenys, Rhamphichthys, and Gym- norhamphichthys (see J.S. Albert and W.G.R. Crampton, p. 364, for key). Library of Congress Cataloging-in-Publication Data Electroreception / Theodore H. Bullock (editor)...[etal.] p. cm. Includes bibliographical references and index. ISBN 0-387-23192-7 1. Electroreceptors. I. Bullock, Theodore Holmes. QP447.5.E44 2005 573.8'7—dc22 2004057843 ISBN 10: 0-387-23192-7 Printed on acid-free paper ISBN 13: 978-0387-23192-1 ᭧ 2005 Springer ScienceϩBusiness Media, Inc. All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer ScienceϩBusiness Media, Inc., 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis.
    [Show full text]
  • Task-Related Sensorimotor Adjustments Increase the Sensory Range in Electrolocation
    The Journal of Neuroscience, January 29, 2020 • 40(5):1097–1109 • 1097 Behavioral/Cognitive Task-Related Sensorimotor Adjustments Increase the Sensory Range in Electrolocation Federico Pedraja,1 XVolker Hofmann,1,2 Julie Goulet,1 and XJacob Engelmann1 1AG Active Sensing, Faculty of Biology/Cluster of Excellence Cognitive Interaction Technology, Bielefeld University, D-33501 Bielefeld, Germany, and 2Department of Physiology, McGill University, Montreal, Quebec H3G 1Y6, Canada Perception and motor control traditionally are studied separately. However, motor activity can serve as a scaffold to shape the sensory flow. This tight link between motor actions and sensing is particularly evident in active sensory systems. Here, we investigate how the weakly electric mormyrid fish Gnathonemus petersii of undetermined sex structure their sensing and motor behavior while learning a perceptual task. We find systematic adjustments of the motor behavior that correlate with an increased performance. Using a model to compute the electrosensory input, we show that these behavioral adjustments improve the sensory input. As we find low neuronal detection thresholds at the level of medullary electrosensory neurons, it seems that the behavior-driven improvements of the sensory input are highly suitable to overcome the sensory limitations, thereby increasing the sensory range. Our results show that motor control isanactivecomponentofsensorylearning,demonstratingthatadetailedunderstandingofcontributionofmotoractionstosensingisneeded to understand even seemingly simple behaviors. Key words: active sensing; behavior; closed-loop control; electrolocation; electroreceptors; learning Significance Statement Motor-guided sensation and perception are intertwined, with motor behavior serving as a scaffold to shape the sensory input. We characterized how the weakly electric mormyrid fish Gnathonemus petersii, as it learns a perceptual task, restructures its senso- rimotor behavior.
    [Show full text]
  • Aspects of Spatiotemporal Integration in Bat Sonar
    Aspects of spatiotemporal integration in bat sonar Dissertation of the Graduate School of Systemic Neurosciences Ludwig-Maximilians-Universität München Submitted by Melina Heinrich Munich, 22nd of December 2014 First Reviewer/Supervisor Prof. Dr. Lutz Wiegrebe Second Reviewer/Supervisor Prof. Dr. Harald Luksch Date of oral defense Munich, 29th of April 2015 This thesis was funded and supported by: The Volkswagenstiftung (I/83838) The Human Frontier Science Program (HFSP RGP 0062/2009) The Graduate School of Systemic Neurosciences (GSN-LMU, DFG-GSC 82/1) To My Family: Future, Present, And Past Index Abstract 1 1 General Introduction 4 Sensory systems and stimulus processing 4 Limitations of sensory systems 5 Passive and active sensory systems 5 Animal biosonar; vision independent representation of space 6 Bats; an introduction 7 General principles of bat sonar 8 x The emitter system 10 o Acoustic signals in echolocating bats 10 x The receiver system 12 o Spatial and temporal information in the bat auditory system 13 Sound localization 16 x Sound localization in the vertical plane 16 x Sound localization in the horizontal plane 17 x Encoding of object distance 18 Integration and resolution in the bat auditory system 19 x Spatial integration and resolution 19 x Temporal integration and resolution 20 Spatiotemporal integration in bat sonar 21 1.1 Study Aim 22 2 The Sonar Aperture and Its Neural Representation in Bats 23 2.1 Reference 23 2.2 Summary 24 2.3 Publication: The Sonar Aperture and Its Neural Representation in Bats 25
    [Show full text]
  • Frequency Selective Encoding of Substrate Vibrations in The
    bioRxiv preprint doi: https://doi.org/10.1101/264747; this version posted February 14, 2018. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 1 Frequency selective encoding of substrate vibrations in the somatosensory cortex 2 3 Mario Prsa and Daniel Huber 4 Department of Basic Neurosciences, University of Geneva, Geneva, Switzerland 5 6 Sensing vibrations that propagate through solid substrates conveys fundamental information about moving objects 7 and other nearby dynamic events. Here we report that neurons responsive to substrate vibrations applied to the 8 mouse forelimb reveal a new way of representing frequency information in the primary somatosensory cortex (S1). In 9 contrast to vibrotactile stimulation of primate glabrous skin, which produces temporally entrained spiking and 10 frequency independent firing rates, we found that mouse S1 neurons rely on a different coding scheme: their spike 11 rates are conspicuously tuned to a preferred frequency of the stimulus. Histology, peripheral nerve block and 12 optogenetic tagging experiments furthermore reveal that these responses are associated with the activation of 13 mechanoreceptors located in deep subdermal tissue of the distal forelimb. We conclude that the encoding of 14 frequency information of substrate‐borne vibrations in the mouse S1 might be analogous to the representation of 15 pitch of airborne sound in auditory cortex. 16 17 Introduction 18 19 Vibrations are ecologically relevant sensory stimuli that can appear in different forms and their spectral content can 20 convey different types of information. For example, the frequency of skin vibrations produced by actively displacing a 21 fingertip across an object provides information about the surface texture.
    [Show full text]
  • Neurons Against Noise Neural Adaptations for Dim Light Vision in Hawkmoths Stöckl, Anna
    Neurons against Noise Neural adaptations for dim light vision in hawkmoths Stöckl, Anna 2016 Document Version: Publisher's PDF, also known as Version of record Link to publication Citation for published version (APA): Stöckl, A. (2016). Neurons against Noise: Neural adaptations for dim light vision in hawkmoths. Lund University, Faculty of Science, Department of Biology. Total number of authors: 1 Creative Commons License: Unspecified General rights Unless other specific re-use rights are stated the following general rights apply: Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal Read more about Creative commons licenses: https://creativecommons.org/licenses/ Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. LUND UNIVERSITY PO Box 117 221 00 Lund +46 46-222 00 00 ANN Printed by Media- A STÖCKL Tr yck, Lund University 2016 Nor Neurons against Noise I. Stöckl, A., O’Carroll D., Warrant E. (2016) Neural summation in the hawkmoth visual system boosts contrast sensitivity dic Ecolabel 3041 0903 and information rate in dim light.
    [Show full text]
  • Implications for Communication
    Integration of the Electrosense with Other Senses: Implications for Communication Stefan Schuster Illstitut fiit Z..l.:tie U, Ll !1td.sität E rr.üt Niihl struLttrtL c..-i e,,,,ii;',,,ä,,,i,Äi;,:i:;l;;,ii,;:l:i::;:,"i',:;:b''3' s' D elt)s' L r'!dt ABSTRACT The outstnndinA ctecbonoro. and elc.trosetrsoN,biliries ,seücdt, oI.lecbi. tish enablc thcn to exchanSe nNüges n,". u.t.n,n"t rt,.,ti, r,_ ..., ,,,.r inn.."ss,Lrr€ r. most oth., animals. llut ",.]j ' 1 .,1 rr.a:.ö\.1..,\ .rd..F.r,.m olerr., ""'': r,h p",r , rr!r LF\.u'1,.".,.,'. ..,,: ..,f,b",,;". ,:'1":.:- \rstrinI,: s rurcri.nrtän!l ., i,,i''' Dr.b.rtrh."','., rr ""ll"iii"i i1,..' " 1",i _i-, 1","f ä, J. l. ,.,, i,il;l i": t-, inrr.(.ur,Jr., I .Lt, i..,*.h.o.rI L,t,; p,*F'., ,.r,.,n" ,n,-.,1.. i,1. ,,"r ,,8,," . ._ a-.i.,-,;",; el€.tric tsn conl.l r",: ,.";; ..;g*Lren.tit fron uritizins morc dran.n o-,.. ,ig,'r.. -po.r.,;;; ä",fi11: prnicrl..llcnd ;,: ä;:*ä ;lj.",:l;l'::':l::J:: ;:,: orsisn.ts s€nr snnuttan.ous\, icrcss se,crar a..*r.. rÄ" rdnrblr nt p.+ *-,rJ U...iir." ble hb,ia!!. rr"o,. r,"l *nna ,n, Pr . "o de r' ll i'l\P'rf i' hc'e r Jr'..',\ ToJ,t ro,.r.t.n,h. J"r..r b or mu,.*n. "'-"""""v'ommrnicarion svst'ms ivitrin a *"rr a+i,,., "*.*,r,i,r.gi.ir;;:;k.
    [Show full text]
  • Behavioural Brain Research Species Differences in Group Size And
    Behavioural Brain Research 207 (2010) 368–376 Contents lists available at ScienceDirect Behavioural Brain Research journal homepage: www.elsevier.com/locate/bbr Research report Species differences in group size and electrosensory interference in weakly electric fishes: Implications for electrosensory processing a, b c d d a,c Sarah A. Stamper ∗, Erika Carrera-G , Eric W. Tan , Vincent Fugère , Rüdiger Krahe , Eric S. Fortune a Department of Psychological and Brain Sciences, Johns Hopkins University, Baltimore, MD, USA b Pontificia Católica del Ecuador, Quito, Ecuador c Department of Neuroscience, Johns Hopkins University, Baltimore, MD, USA d Department of Biology, McGill University, Montreal, QC, Canada article info abstract Article history: In animals with active sensory systems, group size can have dramatic effects on the sensory information Received 13 August 2009 available to individuals. In “wave-type” weakly electric fishes there is a categorical difference in sensory Received in revised form 1 October 2009 processing between solitary fish and fish in groups: when conspecifics are within about 1 m of each other, Accepted 16 October 2009 the electric fields mix and produce interference patterns that are detected by electroreceptors on each Available online 27 October 2009 individual. Neural circuits in these animals must therefore process two streams of information—salient signals from prey items and predators and social signals from nearby conspecifics. We investigated Keywords: the parameters of social signals in two genera of sympatric weakly electric fishes, Apteronotus and Electrotaxis Gymnotiformes Sternopygus, in natural habitats of the Napo River valley in Ecuador and in laboratory settings. Apterono- Electrosensory tus were most commonly found in pairs along the Napo River (47% of observations; maximum group Social behavior size 4) and produced electrosensory interference at rates of 20–300 Hz.
    [Show full text]