DOCSLIB.ORG

Physical Metallurgy (異質成核推導補充)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Physical metallurgy Nucleation and growth kinetics (異質成核推導補充) Materials Science and EngineeringPhase Transformations in Metals Homogeneous Nucleation Gibbs free energy (G) - Gibbs free energy is a function of the internal energy of the system (enthalpy, H) and a measurement of the randomness or disorder of the atoms or molecules (entropy, S). - A transformation will occur spontaneously only when the change in free energy G has a negative value. Case of homogeneous nucleation - For the sake of simplicity, let us first consider the solidification of a pure material, and that nuclei of the solid phase form in the interior of the liquid as atoms cluster together so as to form a packing arrangement similar to that found in the solid phase. - There are two contributions to the total free energy change that accompany a solidification transformation. The first is the free energy difference between the solid and liquid phases, or the volume free energy, Gv. The second energy contribution results from the formation of the solid–liquid phase boundary during the solidification transformation, or the surface energy, . FIGURE 12.1 Schematic diagram showing the nucleation of a spherical solid particle in a liquid. 2 Materials Science and EngineeringPhase Transformations in Metals Homogeneous Nucleation 4 3 2 V: volume of spherical nucleus, G VGv A r Gv 4r 3 G : volume free energy, d(G) v When r = r* 4r 2G 8r 0 A: surface area of spherical nucleus, dr v : surface free energy, 2 r* r: radius of spherical nucleus, Gv 3 r*: critical radius of spherical nucleus, 4 2 3 2 2 16 G* ( ) Gv 4 ( ) 2 G*: critical free energy, activation energy 3 Gv Gv 3(Gv ) FIGURE 12. 2 (a) Schematic curves for volume free energy and surface free energy contributions to the total free energy change attending the formation of a spherical embryo/nucleus during Solidification, (b) Schematic plot of free energy versus embryo/nucleus radius, on which is 3 shown the critical free energy change (G*) and the critical nucleus radius (r*). Materials Science and EngineeringPhase Transformations in Metals Homogeneous Nucleation The volume free energy change Gv is the driving force for the solidification transformation, and its magnitude is a function of temperature. At the equilibrium solidification temperature Tm, the value of Gv is zero, and with diminishing temperature its value becomes increasingly more negative. It can be shown that Gv is a function of temperature as H f (Tm T) Gv Tm 2 2 2T 1 r* m H (T T) Gv f m H f Tm T Tm 16 3 16 3 16 3T 2 1 G* m 3(G ) 2 2 3H 2 (T T ) 2 v H f (Tm T ) f m 3 Tm Hf: latent heat of fusion, Tm: equilibrium melting temperature (K), T: real solidification temperature (K), 4 Materials Science and EngineeringPhase Transformations in Metals Homogeneous Nucleation Both the critical radius r* and the activation free energy G* decrease as temperature T decreases. With a lowering of temperature at temperatures below the equilibrium solidification temperature (Tm), nucleation occurs more readily. 2T 1 16 3T 2 1 r* m G* m H T T 2 2 f m 3H f (Tm T) < FIGURE 12.3 Schematic free energy- versus-embryo/nucleus radius curves for two different temperatures. The critical free energy change (G*) and critical nucleus radius (r*) are Indicated for each temperature. 5 Materials Science and EngineeringPhase Transformations in Metals Nucleation rate The number of stable nuclei n* (having radii greater than r*) is a function of temperature as Where K1 is related to the total number of nuclei of the solid phase Another temperature-dependent step influences nucleation: the clusting of atoms by short-range diffusion during the formation of nuclei. The diffusion effect is related to the frequency at which atoms from the liquid attach themselves to the solid nucleus, d. Where Qd is a temperature-independent parameter-the activation energy for diffusion, and K2 is a temperature-dependenct constant. A decrease of temperature results in a reduction in d. The nucleation rate is simply proportional to the product of n* and d, that is 6 Materials Science and EngineeringPhase Transformations in Metals FIGURE 12.4 For Solidification: (a) number of stable nuclei v.s. temperature, (b) frequency of atomic attachment v.s. temperature and (c) nucleation rate v.s. temperature. 7 Materials Science and EngineeringPhase Transformations in Metals Heterogeneous Nucleation In practical supercoolings are often on the order of only several degrees Celsius.The reason for this is that the activation energy for nucleation is lowered when nuclei form on preexisting surfaces or interfaces, since the surface free energy is reduced. In other words, it is easier for nucleation to occur at surfaces and interfaces than at other sites. Again, this type of nucleation is termed heterogeneous. Let us consider the nucleation, on a flat surface, of a solid particle from a liquid phase. It is assumed that both the liquid and solid phases “wet” this flat surface, that is, both of these phases spread out and cover the surface. IL SI SL cos FIGURE 12.5 Heterogeneous nucleation of a solid from a liquid. The solid–surface (SI), solid–liquid (SL), and liquid–surface (IL) interfacial energies are represented by vectors. The wetting angle () is also shown. 8 Materials Science and EngineeringPhase Transformations in Metals Heterogeneous Nucleation 2 ASI (r sin ) 2 ASL 2r (1 cos ) r 3 V (2 3cos cos3 ) r sin r sin S 3 r r Ghet VS Gv ASL SL ASI SI ASI IL Ghet G S() 3 4r 2 VS: volume of heterogeneous nucleus, G G 4r IL SI SL cos 3 v SL Gv: volume free energy, (2 cos )(1 cos ) 2 ASL: area of solid-liquid interface, S() 4 ASI: area of solid-surface interface, 2 SL SL: surface free energy of solid-liquid interface, r* Gv SI: surface free energy of solid-surface interface, 3 r: radius of spherical nucleus, * 16 SL Ghet 2 S() r*: critical radius of spherical nucleus, 3(Gv ) G *: critical free energy, activation energy * * het Ghet Ghom S( ) 9 Materials Science and EngineeringPhase Transformations in Metals Heterogeneous Nucleation 16 3T 2 1 G* m 2 2 3H f (Tm T) G * Q N exp( )exp( d ) kT kT * * Ghet Ghom S( ) 2 3cos cos3 S() 4 FIGURE 12.6 Schematic free energy-versus- FIGURE 12.7 Nucleation rate versus embryo/nucleus radius plot on which is presented temperature for both homogeneous and curves for both homogeneous and heterogeneous heterogeneous nucleation. Degree of nucleation. Critical free energies and the critical supercooling (T) for each is also shown. radius are also shown. 10 Materials Science and EngineeringPhase Transformations in Metals Heterogeneous versus Homogeneous Nucleation Critical radius The critical radius for heterogeneous nucleation is the same as for homogeneous. Activation energy The activation energy barrier for heterogeneous nucleation is smaller than the homogeneous barrier. Supercooling A much smaller degree of supercooling is required for heterogeneous nucleation. 11 Materials Science and EngineeringPhase Transformations in Metals Growth The growth step in a phase transformation begins once an embryo has exceeded the critical size, r*, and becomes a stable nucleus. The growth process will cease in any region where particles of the new phase meet, since here the transformation will have reached completion. Particle growth occurs by long-range atomic diffusion, which normally involves several steps- for example, diffusion through the parent phase, across a phase boundary, and then into the nucleus. Consequently, the growth rate is determined by the rate of diffusion, and its temperature dependence is the same as for the diffusion coefficient, Q G C exp kT Q: activation energy, independent of temperature; C: constant, independent of temperature. At some temperature, the overall transformation rate is equal to some product of N and G. The third curve for the total rate represents this combined effect. The general shape of this curve is the same as for the nucleation rate, in that it has a peak or maximum that has been shifted upward relative to the curve. FIGURE 12.8 Schematic plot showing curves for nucleation rate (N), growth rate (G), and overall12 transformation versus temperature. Materials Science and EngineeringPhase Transformations in Metals Growth As we shall see below, the rate of transformation and the time required for the transformation to proceed to some degree of completion are inversely proportional to one another. First, the size of the product phase particles will depend on transformation temperature. Secondly, when a material is cooled very rapidly through the temperature range encompassed by the transformation rate curve to a relatively low temperature where the rate is extremely low, it is possible to produce nonequilibrium phase structures. FIGURE 12.9 Schematic plots of (a) transformation rate versus temperature, and (b) logarithm time [to some degree (e.g., 0.5 fraction) of transformation] versus temperature. The curves in both (a) and (b) are generated from the same set of data—i.e., for horizontal axes, the time 13 [scaled logarithmically in the (b) plot] is just the reciprocal of the rate from plot (a). 相變態 Heterogeneous Nucleation Driving force and critical size of heterogeneous nucleation - Balance among tensions SLsin Consider a solid embryo forming in contact with a perfectly flat mold wall as depicted in Fig. 4.7. Assuming SL is isotropic, the total interfacial energy of the system SLcos is minimized if the embryo has the shape of a spherical cap. Fig. 4.7 Heterogeneous nucleation of spherical ML SM SL cos (4.14) cap on a flat mold wall. cos ML SM SL SL: solid/liquid interfacial tension, ML: mold/liquid interfacial tension, SM: solid/mold interfacial tension, : a wetting angle.
Recommended publications
  • Thermodynamics and Kinetics of Nucleation in Binary Solutions

    Thermodynamics and Kinetics of Nucleation in Binary Solutions

    1 Thermodynamics and kinetics of nucleation in binary solutions Nikolay V. Alekseechkin Akhiezer Institute for Theoretical Physics, National Science Centre “Kharkov Institute of Physics and Technology”, Akademicheskaya Street 1, Kharkov 61108, Ukraine Email: [email protected] Keywords: Binary solution; phase equilibrium; binary nucleation; diffusion growth; surface layer. A new approach that is a combination of classical thermodynamics and macroscopic kinetics is offered for studying the nucleation kinetics in condensed binary solutions. The theory covers the separation of liquid and solid solutions proceeding along the nucleation mechanism, as well as liquid-solid transformations, e.g., the crystallization of molten alloys. The cases of nucleation of both unary and binary precipitates are considered. Equations of equilibrium for a critical nucleus are derived and then employed in the macroscopic equations of nucleus growth; the steady state nucleation rate is calculated with the use of these equations. The present approach can be applied to the general case of non-ideal solution; the calculations are performed on the model of regular solution within the classical nucleation theory (CNT) approximation implying the bulk properties of a nucleus and constant surface tension. The way of extending the theory beyond the CNT approximation is shown in the framework of the finite- thickness layer method. From equations of equilibrium of a surface layer with coexisting bulk phases, equations for adsorption and the dependences of surface tension on temperature, radius, and composition are derived. Surface effects on the thermodynamics and kinetics of nucleation are discussed. 1. Introduction Binary nucleation covers a wide class of processes of phase transformations which can be divided into three groups: (i) gas-liquid (or solid) transformations, (ii) liquid-gas transformations, and (iii) transformations within a condensed state.
  • Determination of Supercooling Degree, Nucleation and Growth Rates, and Particle Size for Ice Slurry Crystallization in Vacuum

    Determination of Supercooling Degree, Nucleation and Growth Rates, and Particle Size for Ice Slurry Crystallization in Vacuum

    crystals Article Determination of Supercooling Degree, Nucleation and Growth Rates, and Particle Size for Ice Slurry Crystallization in Vacuum Xi Liu, Kunyu Zhuang, Shi Lin, Zheng Zhang and Xuelai Li * School of Chemical Engineering, Fuzhou University, Fuzhou 350116, China; [email protected] (X.L.); [email protected] (K.Z.); [email protected] (S.L.); [email protected] (Z.Z.) * Correspondence: [email protected] Academic Editors: Helmut Cölfen and Mei Pan Received: 7 April 2017; Accepted: 29 April 2017; Published: 5 May 2017 Abstract: Understanding the crystallization behavior of ice slurry under vacuum condition is important to the wide application of the vacuum method. In this study, we first measured the supercooling degree of the initiation of ice slurry formation under different stirring rates, cooling rates and ethylene glycol concentrations. Results indicate that the supercooling crystallization pressure difference increases with increasing cooling rate, while it decreases with increasing ethylene glycol concentration. The stirring rate has little influence on supercooling crystallization pressure difference. Second, the crystallization kinetics of ice crystals was conducted through batch cooling crystallization experiments based on the population balance equation. The equations of nucleation rate and growth rate were established in terms of power law kinetic expressions. Meanwhile, the influences of suspension density, stirring rate and supercooling degree on the process of nucleation and growth were studied. Third, the morphology of ice crystals in ice slurry was obtained using a microscopic observation system. It is found that the effect of stirring rate on ice crystal size is very small and the addition of ethylene glycoleffectively inhibits the growth of ice crystals.
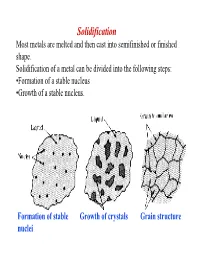
  • Solidification Most Metals Are Melted and Then Cast Into Semifinished Or Finished Shape

    Solidification Most Metals Are Melted and Then Cast Into Semifinished Or Finished Shape

    Solidification Most metals are melted and then cast into semifinished or finished shape. Solidification of a metal can be divided into the following steps: •Formation of a stable nucleus •Growth of a stable nucleus. Formation of stable Growth of crystals Grain structure nuclei Polycrystalline Metals In most cases, solidification begins from multiple sites, each of which can produce a different orientation The result is a “polycrystalline” material consisting of many small crystals of “grains” Each grain has the same crystal lattice, but the lattices are misoriented from grain to grain Driving force: solidification ⇒ For the reaction to proceed to the right ∆G AL AS V must be negative. • Writing the free energies of the solid and liquid as: S S S GV = H - TS L L L GV = H - TS ∴∴∴ ∆GV = ∆H - T∆S • At equilibrium, i.e. Tmelt , then the ∆GV = 0 , so we can estimate the melting entropy as: ∆S = ∆H/Tmelt where -∆H is the latent heat (enthalpy) of melting. • Ignore the difference in specific heat between solid and liquid, and we estimate the free energy difference as: T ∆H × ∆T ∆GV ≅ ∆H − ∆H = TMelt TMelt NUCLEATION The two main mechanisms by which nucleation of a solid particles in liquid metal occurs are homogeneous and heterogeneous nucleation. Homogeneous Nucleation Homogeneous nucleation occurs when there are no special objects inside a phase which can cause nucleation. For instance when a pure liquid metal is slowly cooled below its equilibrium freezing temperature to a sufficient degree numerous homogeneous nuclei are created by slow-moving atoms bonding together in a crystalline form.
  • Nucleation Theory: a Literature Review and Applications to Nucleation Rates of Natural Gas Hydrates

    Nucleation Theory: a Literature Review and Applications to Nucleation Rates of Natural Gas Hydrates

    Nucleation Theory: A Literature Review and Applications to Nucleation Rates of Natural Gas Hydrates Simon Davies SUMMARY Predicting the onset of hydrate nucleation in oil pipelines is one of the most challenging aspects in the flow assurance modelling work being performed at the Center for Hydrate Research. Nucleation is initiated by a random fluctuation which is able to overcome the energy barrier for the phase transition, once such a fluctuation occurs, further growth is energetically favourable. Historically the random fluctuation requires for nucleation was defined as the formation of a nucleus of critical size. Recently, more realistic models have been proposed based on density functional theory. In this report, a literature survey of nucleation theory was performed in order to determine the state-of-the-art understanding of hydrate nucleation. A simplified nucleation model was then designed based on a two dimensional Ising model, in order to determine thermodynamic properties for nuclei of various sizes. The model used window sampling to collect high resolution statistics for the high energy states. It was demonstrated that the shape and height of the energy barrier can be determined for a nucleating system in this way. INTRODUCTION The ability to predict the onset of nucleation is important for a wide variety of first order phase transitions from industrial crystallisers to rainfall. Systems can be held in a supersaturated state for significant periods of time before a phase transition occurs: distilled water can be held indefinitely at -10ºC without freezing, with further purification it can be cooled to -30ºC without freezing [1]. Predicting the onset of hydrate nucleation in oil pipelines is one of the most challenging aspects in the flow assurance modelling work being performed at the Center for Hydrate Research.
  • Crystallization of Supercooled Liquid Elements Induced by Superclusters Containing Magic Atom Numbers Robert F

    Crystallization of Supercooled Liquid Elements Induced by Superclusters Containing Magic Atom Numbers Robert F

    Crystallization of Supercooled Liquid Elements Induced by Superclusters Containing Magic Atom Numbers Robert F. Tournier, CRETA /CNRS, Université Joseph Fourier, B.P. 166, 38042 Grenoble cedex 09, France. E-mail: [email protected]; Tel.: +33-608-716-878; Fax: +33-956-705-473. Abstract: A few experiments have detected icosahedral superclusters in undercooled liquids. These superclusters survive above the crystal melting temperature Tm because all their surface atoms have the same fusion heat as their core atoms and are melted by liquid homogeneous and heterogeneous nucleation in their core, depending on superheating time and temperature. They act as heterogeneous growth nuclei of crystallized phase at a temperature Tc of the undercooled melt. They contribute to the critical barrier reduction, which becomes smaller than that of crystals containing the same atom number n. After strong superheating, the undercooling rate is still limited because the nucleation of 13-atom superclusters always reduces this barrier, and increases Tc above a homogeneous nucleation temperature equal to Tm/3 in liquid elements. After weak superheating, the most stable superclusters containing n = 13, 55, 147, 309 and 561 atoms survive or melt and determine Tc during undercooling, depending on n and sample volume. The experimental nucleation temperatures Tc of 32 liquid elements and the supercluster melting temperatures are predicted with sample volumes varying by 18 orders of magnitude. The classical Gibbs free energy change is used, adding an enthalpy saving related to the Laplace pressure change associated with supercluster formation, which is quantified for n=13 and 55. Keywords: thermal properties, solid-liquid interface energy, crystal nucleation, undercooling, superclusters, liquid-solid transition, overheating, non-metal to metal transition in cluster, Laplace pressure 1.
  • Comparison of Classical Nucleation Theory and Modern Theory of Phase

    Comparison of Classical Nucleation Theory and Modern Theory of Phase

    ed Chem nc i a ca Baranov, J Adv Chem Eng 2017, 7:1 v l d E A n f g DOI: 10.4172/2090-4568.1000177 o i n l e Journal of Advanced a e n r r i n u g o J ISSN: 2090-4568 Chemical Engineering Research Article Open Access Comparison of Classical Nucleation Theory and Modern Theory of Phase Transition Baranov SA1,2,3* 1Institute of Applied Physics, Academy of Sciences of Moldova, Republic of Moldova 2Department de Genie Physique, Ecole Polytechnique de Montreal, Montreal H3C 3A7, Quebec, Canada 3Shevchenko Transnistria State University, Tiraspol, Republic of Moldova Abstract The formation of electrochemical phase is a typical example of a first-order phase transition. An overview on old and new thermodynamic and kinetic aspects of the theoretical description of first-order phase transitions, and, in particular, of the theory of nucleation is given. Electrochemical nucleation of nanostructures has been considered in terms of the classical Gibbs and the Cahn-Hilliard-Hillert theories. We obtained agreement between the theories Kahn-Hilliard-Hillert and Gibbs. Keywords: Electrochemistry; Nucleation; Nanoparticles; Phase rc=2γ/μ transitions; Gibbs theory; Cahn-Hilliard theory Critical nucleus radius corresponding to maximum G3 is as follows Introduction (Figure 1) [1-9]: 32 (5) Electrochemical nucleation is usually described in the framework ∆G3 =(16π / 3)( γµ33 / ) of the classical Gibbs theory of nucleation, which provides a simple For a two-dimensional case, we obtain [1-9] expression for the critical radius of a growing nucleus (nanoparticles) 2 [1-11]: ∆=G2 =G 2P / 2πγ (2 / µ2 ) where γ2 is the specific surface energy (for the two-dimensional rc=К(γ/μ) 1 case), μ3 is the change in volume energy during a phase transition (for where γ is the specific surface energy, μ is the change in volume the two-dimensional case).
  • Origins of the Failure of Classical Nucleation Theory for Nanocellular Polymer Foams

    Origins of the Failure of Classical Nucleation Theory for Nanocellular Polymer Foams

    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of Waterloo's Institutional Repository Origins of the Failure of Classical Nucleation Theory for Nanocellular Polymer Foams Yeongyoon Kim,1 Chul B. Park,2 P. Chen,3, 4 and Russell B. Thompson1,4, ∗ 1Department of Physics and Astronomy, University of Waterloo, 200 University Avenue West, Waterloo, Ontario, Canada N2L 3G1 2Microcellular Plastics Manufacturing Laboratory, Department of Mechanical and Industrial Engineering, University of Toronto, 5 King’s College Road, Toronto, Ontario, Canada M5S 3G8 3Department of Chemical Engineering, University of Waterloo, 200 University Avenue West, Waterloo, Ontario, Canada N2L 3G1 4Waterloo Institute for Nanotechnology, University of Waterloo, 200 University Avenue West, Waterloo, Ontario, Canada N2L 3G1 This document is the accepted manuscript version of a published article. Published by The Royal Society of Chemistry in the journal "Soft Matter" issue 16, DOI: 10.1039/C1SM05575E 1 Abstract Relative nucleation rates for fluid bubbles of nanometre dimensions in polymer matrices are calculated using both classical nucleation theory and self-consistent field theory. An identical model is used for both calculations showing that classical nucleation theory predictions are off by many orders of magnitude. The main cause of the failure of classical nucleation theory can be traced to its representation of a bubble surface as a flat interface. For nanoscopic bubbles, the curvature of the bubble surface is comparable to the size of the polymer molecules. Polymers on the outside of a curved bubble surface can explore more conformations than can polymers next to a flat interface.
  • Applications

    Applications

    PHY474 Applications Ulrich Z¨urcher∗ Physics Department, Cleveland State University, Cleveland, OH 44115 (Dated: November 14, 2008) PACS numbers: 05.70 I. PHASE TRANSFORMATION OF PURE not coexist (in equilibrium): ice directy sublimates into SUBSTANCES vapor. Sublimation of dry ice [carbondioxide]. the triple point lies above atmospheric pressure. Most substances: The curve of pressure vs volume for a quantity of applying more pressure raises the melting temperature. matter at constant temperature is determined by the Ice is different: applying more pressure lowers its melting Gibbs free energy of the substance. The curve is called temperature: this is related to the fact that density of ice isotherm. We consider the isotherms of a real gas in is lower than density of liquid. which atoms associate together in a liquid or solid phase. Liquid-gas phase boundary always has a poisitive A phase is a prortion of the system that is uniform in slope: if you increase temperature you must increase composition. pressure to prevent liquid from vaporizing. As pressure Two phases may coexist with a definite boundary be- increases, density of gas is increasing so gas and liquid tween them. An isotherm may show a region in the PV become indistinguishable. Eventually there is a point when there is no longer a discontinuous transition: crit- diagram in which liquid and gas coexist in equilibrium ◦ with each other. There are isotherms at low tempera- ical point. For water it is 374 C and 221 bars. Close to tures for which solids and liquids coexist and isotherms the critical point we call the system “fluid." for which solids and gases coexist.
  • Introduction to the Physics of Nucleation

    Introduction to the Physics of Nucleation

    C. R. Physique 7 (2006) 946–958 http://france.elsevier.com/direct/COMREN/ Nucleation/Nucléation Introduction to the physics of nucleation Humphrey J. Maris Department of Physics, Brown University, Providence, RI 02912, USA Available online 28 November 2006 Abstract In this introductory article, I review the theory of nucleation by thermal activation and by quantum tunneling. The effect of heterogeneous nucleation at surfaces is discussed and a brief survey of experimental techniques is given. To cite this article: H.J. Maris, C. R. Physique 7 (2006). © 2006 Académie des sciences. Published by Elsevier Masson SAS. All rights reserved. Résumé Introduction à la physique de la nucléation. Dans cet article introductif, je passe en revue la théorie de la nucléation par activation thermique et par effet tunnel quantique. Je discute les effets de la nucléation hétérogène aux surfaces et je propose un bref survol des techniques expérimentales utilisées. Pour citer cet article : H.J. Maris, C. R. Physique 7 (2006). © 2006 Académie des sciences. Published by Elsevier Masson SAS. All rights reserved. Keywords: Nucleation; Phase transitions Mots-clés : Nucleation ; Transitions de phase This issue contains a number of reviews all concerning different aspects of nucleation. In this introduction, I briefly summarize the basic theory of nucleation processes and then mention some selected topics of interest. Nucleation means a change in a physical or chemical system that begins within a small region, that is to say, that begins at a nucleus. The very long history of this subject has been reviewed by G.S. Kell [1] who credits Huyghens with having in 1662 performed the first experiments with metastable water under tension.
  • MSE Problems

    MSE Problems

    Materials Science and Engineering Problems MSE Faculty April 19, 2021 This document includes the assigned problems that have been included so far in the digitized portion of our course curriculum. Contents 1 301 Problems 3 1.1 Course Organization.................................................. 3 1.2 Atomic Structure and Bonding ............................................ 3 1.3 Crystal Structure .................................................... 5 1.4 Imperfections ...................................................... 8 1.5 Electrical Properties................................................... 10 1.6 Diffusion......................................................... 12 1.7 Phase Diagrams..................................................... 14 1.8 Phase Transformations................................................. 18 1.9 Mechanical Properties ................................................. 18 1.10 Fracture Mechanics................................................... 22 1.11 Corrosion......................................................... 23 1.12 Ceramics......................................................... 24 1.13 Polymers......................................................... 25 2 314 Problems 27 2.1 Phases and Components................................................ 27 2.2 Intensive and Extensive Properties.......................................... 27 2.3 Differential Quantities and State Functions ..................................... 27 2.4 Entropy.......................................................... 27 2.5
  • Chapter 10: Phase Transformations

    Chapter 10: Phase Transformations

    Chapter 10: Phase Transformations ISSUES TO ADDRESS... • Transforming one phase into another takes time. Fe Fe C Eutectoid 3 g transformation (cementite) (Austenite) + a C FCC (ferrite) (BCC) • How does the rate of transformation depend on time and T? • How can we slow down the transformation so that we can engineering non-equilibrium structures? • Are the mechanical properties of non-equilibrium structures better? Chapter 10 - 1 Phase transformation • Takes time (transformation rates: kinetics). • Involves movement/rearrangement of atoms. • Usually involves changes in microstructure 1. “Simple” diffusion-dependent transformation: no change in number of compositions of phases present (e.g. solidification of pure elemental metals, allotropic transformation, recrystallization, grain growth). 2. Diffusion-dependent transformation: transformation with alteration in phase composition and, often, with changes in number of phases present (e.g. eutectoid reaction). 3. Diffusionless transformation: e.g. rapid T quenching to “trap” metastable phases. Chapter 10 - 2 º TR = recrystallization temperature TR Adapted from Fig. 7.22, Callister 7e. The influence of annealing T on the tensile strength and ductility of a brass alloy. º Chapter 10 - 3 Iron-Carbon Phase Diagram Eutectoid cooling: cool g (0.76 wt% C) a (0.022 wt% C) + Fe3C (6.7 wt% C) T(°C) heat 1600 d 1400 L g g+L 1200 A L+Fe C (austenite) 1148°C 3 R S 1000 g g g+Fe C g g 3 800a B 727°C = Teutectoid R S (cementite) C 3 600 a+Fe C 3 Fe 400 0 1 2 3 4 5 6 6.7 0.76 4.30 (Fe) Co, wt% C Fe3C (cementite-hard) a (ferrite-soft) eutectoid Adapted from Fig.
  • MSE3 Ch07 Precipitation

    MSE3 Ch07 Precipitation

    Chapter 7 Copyright © 2011, 2015 by Roland Stull. Meteorology for Scientists and Engineers, 3rd Ed. preCipitation Contents Hydrometeors are liquid and ice parti- cles that form in the atmosphere. Hydrom- Supersaturation and Water Availability 186 eter sizes range from small cloud droplets Supersaturation 186 7 and ice crystals to large hailstones. Precipitation Water Availability 186 occurs when hydrometeors are large and heavy Number and Size of Hydrometeors 187 enough to fall to the Earth’s surface. Virga occurs Nucleation of Liquid Droplets 188 when hydrometers fall from a cloud, but evaporate Cloud Condensation Nuclei (CCN) 188 before reaching the Earth’s surface. Curvature and Solute Effects 189 Precipitation particles are much larger than cloud Critical Radius 192 particles, as illustrated in Fig. 7.1. One “typical” Haze 192 Activated Nuclei 193 raindrop holds as much water as a million “typical” cloud droplets. How do such large precipitation Nucleation of Ice Crystals 194 Processes 194 particles form? Ice Nuclei 195 The microphysics of cloud- and precipitation- particle formation is affected by super-saturation, Liquid Droplet Growth by Diffusion 196 nucleation, diffusion, and collision. Ice Growth by Diffusion 198 Supersaturation indicates the amount of excess Ice Crystal Habits 198 water vapor available to form rain and snow. Growth Rates 200 The Wegener-Bergeron-Findeisen (WBF) Nucleation is the formation of new liquid or Process 201 solid hydrometeors as water vapor attaches to tiny dust particles carried in the air. These particles are Collision and Collection 202 Terminal Velocity of Hydrometeors 202 called cloud condensation nuclei or ice nuclei. Cloud Droplets 202 Diffusion is the somewhat random migration Rain Drops 203 of water-vapor molecules through the air toward ex- Hailstones 204 isting hydrometeors.