DOCSLIB.ORG

MSE3 Ch07 Precipitation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
MSE3 Ch07 Precipitation Chapter 7 Copyright © 2011, 2015 by Roland Stull. Meteorology for Scientists and Engineers, 3rd Ed. preCipitation Contents Hydrometeors are liquid and ice parti- cles that form in the atmosphere. Hydrom- Supersaturation and Water Availability 186 eter sizes range from small cloud droplets Supersaturation 186 7 and ice crystals to large hailstones. Precipitation Water Availability 186 occurs when hydrometeors are large and heavy Number and Size of Hydrometeors 187 enough to fall to the Earth’s surface. Virga occurs Nucleation of Liquid Droplets 188 when hydrometers fall from a cloud, but evaporate Cloud Condensation Nuclei (CCN) 188 before reaching the Earth’s surface. Curvature and Solute Effects 189 Precipitation particles are much larger than cloud Critical Radius 192 particles, as illustrated in Fig. 7.1. One “typical” Haze 192 Activated Nuclei 193 raindrop holds as much water as a million “typical” cloud droplets. How do such large precipitation Nucleation of Ice Crystals 194 Processes 194 particles form? Ice Nuclei 195 The microphysics of cloud- and precipitation- particle formation is affected by super-saturation, Liquid Droplet Growth by Diffusion 196 nucleation, diffusion, and collision. Ice Growth by Diffusion 198 Supersaturation indicates the amount of excess Ice Crystal Habits 198 water vapor available to form rain and snow. Growth Rates 200 The Wegener-Bergeron-Findeisen (WBF) Nucleation is the formation of new liquid or Process 201 solid hydrometeors as water vapor attaches to tiny dust particles carried in the air. These particles are Collision and Collection 202 Terminal Velocity of Hydrometeors 202 called cloud condensation nuclei or ice nuclei. Cloud Droplets 202 Diffusion is the somewhat random migration Rain Drops 203 of water-vapor molecules through the air toward ex- Hailstones 204 isting hydrometeors. Conduction of heat away from Collection & Aggregation Processes 204 the droplet is also necessary to compensate the la- Warm-cloud Process 204 tent heating of condensation or deposition. Cold-cloud Processes 205 Collision between two hydrometeors allows Precipitation Formation 205 them to combine into larger particles. These pro- Warm Clouds 205 cesses affect liquid water and ice differently. Cold Clouds 206 Precipitation Characteristics 207 Rain-Drop Size Distribution 207 Rainfall Rates 208 Snowfall Rates & Snow Accumulation 208 7PMVNF NN Precipitation Distribution 209 m m m m Precipitation Measurement 210 Summary 211 TNBMMDMPVE 3N Threads 211 UZQJDBMDMPVE 3N Exercises 212 MBSHFDMPVE 3N Numerical Problems 212 Understanding & Critical Evaluation 214 ESJ[[MF 3N Web-Enhanced Questions 217 TNBMMSBJO 3N Synthesis Questions 217 )ZESPNFUFPS UZQJDBMSBJO 3N “Meteorology for Scientists and Engineers, 3rd Edi- MBSHFSBJO tion” by Roland Stull is licensed under a Creative 3N Commons Attribution-NonCommercial-ShareAlike 4.0 International License. To view a copy of the license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ . This work is Figure 7.1 available at http://www.eos.ubc.ca/books/Practical_Meteorology/ . Drop volumes and radii, R. 185 186 chapter 7 PRECIPITATIoN S HLH 1IZTJDBM S HLH 4JUVBUJPO supersaturation and Water BEJBCBUNPJTU availability 1 S& S L1B ST 9 5 supersaturation When there is more water vapor in the air than it can hold at equilibrium, the air is said to be super- saturated. Supersaturated air has relative humid- -$- JTPIVNF ity RH greater than 100%. Define this excess relative ESZBEJBCBU BJS QBSDFM humidity as a supersaturation fraction S: SJTF S = RH – 1 •(7.1) 9 m m or as a supersaturation percentage S%: 5 $ S% = 100% · S = RH% – 100% •(7.2) Figure 7.2 Thermo diagram (emagram) showing how excess-water mixing Using the definition of relative humidity from ratio rE (thick line with arrows at each end) increases with in- the Moisture chapter, rewrite supersaturation in creasing height above cloud base (LCL) for an air parcel rising terms of total vapor pressure e and saturation vapor adiabatically. r = total water mixing ratio; r = saturation T s pressure e : mixing ratio for water vapor. r is the amount of water that can s e E S 1 form hydrometeors. = − •(7.3) es for e > es. It can also be approximated using mixing ratios: r S ≈ − 1 •(7.4) r Solved Example s An air parcel starts at 100 kPa with temperature for r > rs. 20°C and mixing ratio 4 g/kg. Use a thermo diagram to find the adiabatic value of excess-water mixing ratio when the parcel reaches a pressure of 60 kPa, and find Water availability the max available supersaturation. Suppose that an initially-unsaturated air parcel has total water mixing ratio of rT. If the air parcel Solution rises adiabatically (i.e., no mixing with the environ- Given: Initially r = rT = 4 g/kg, T = 20°C, P = 100 kPa ment, and no precipitation in or out), then it cools Finally: P = 60 kPa. and its saturation mixing ratio decreases. You can Find: rE = ? g/kg, SA = ? (dimensionless) use a thermo diagram (from the Stability chapter) to find these changing mixing ratios, as sketched here Use a full size thermo diagram from the Stability chap- in Fig. 7.2. ter. Starting with the initial conditions, and following Above the parcel’s lifting condensation level the air parcel up dry-adiabatically from the surface, we (LCL) the saturation mixing ratio r is less than r . find the LCL is atP = 75 kPa and T = –3°C, which marks s T This supersaturated air has an excess water mix- cloud-base. Above the LCL, follow the moist adiabat, ing ratio rE of: which gives T ≈ –15°C at rs = 2 g/kg at P = 60 kPa. As- suming no entrainment and mixing, rT = 4 g/kg. rE = rT – rs •(7.5) Use eq. (7.5): rE = (4 – 2) g/kg = 2 g/kg. Then use eq. (7.7): SA = rE/rs = 1 = 100%. The excess water is available to condense onto liquid drops and to deposit onto ice crystals: Check: Units OK. Physics OK. Agrees with Figs. 7.2 & 7.3) rL + ri = rE (7.6) Discussion: A supersaturation of 100% corresponds to a relative humidity of RH = 200% from eq. (7.2). Thus, where rL is liquid-water mixing ratio, and ri is ice there is twice as much water in the air as can be held at mixing ratio. At temperatures T in the range –40 < T equilibrium. This excess water vapor drives conden- < 0°C, supercooled liquid water and ice crystals can sation. For real clouds, we expect r in the range of 0.5 E co-exist in the air. to 1.5 g/kg, based on the curves in Fig. 7.3. R. STULL • METEoRoLoGy FoR SCIENTISTS AND ENGINEERS 187 Available supersaturation fraction is defined 1IZTJDBM as: 4JUVBUJPO rE rT S = = − 1 & A r r (7.7) s s 1 As hydrometeors grow and remove water vapor, r L1B 5ZQJDBMS becomes less than rT, and S becomes less than SA. & Droplets and ice crystals stop growing by condensa- tion and deposition when they have consumed all "EJBCBUJDS the available supersaturation (i.e., when r → rs and S → 0). BJS The adiabatic estimate of r increases with QBSDFM E SJTF height above the LCL, as sketched in Figs. 7.2 and 7.3. However, in many real clouds, diabatic (i.e., non-adiabatic) processes such as entrainment and mixing of clear drier air into the top and sides of the cloud cause the total-water mixing ratio to not be S& HLH conserved with height. As a result, typical amounts of excess-water mixing ratio are less than adiabatic Figure 7.3 (dashed lines in Fig. 7.3). Example of the increase of excess water mixing ratio rE vs. Beware that the adiabatic rE curve varies from height above cloud base for the scenario in the previous figure. situation to situation, depending on the thermody- The adiabatic value (solid line) represents the max likely value in namic initial conditions of the air parcel. So Fig. 7.3 non-precipitating clouds, while the dashed curves show ranges is just one example (based on the Fig. 7.2 scenario). of actual max values. P is pressure. number and size of hydrometeors Suppose we partition the available excess wa- ter equally between all hydrometeors (for example, for all liquid water droplets). In this way, we can Solved Example estimate the average radius R for each droplet due Within a cloud, suppose air density is 1 kg/m3 and only to condensation (i.e., before collisions between the excess water mixing ratio is 4 g/kg. Find the final droplets allow some to merge and grow into larger drop radius for hydrometeor counts of (a) 108/m3, and drops): (b) 109/m3 . 1/ 3 3 ρ r R = ··air E •(7.8) Solution 3 4π ρwater n Given: rE = 0.004 kgwater/kgair, ρair = 1 kg/m n = (a) 108/m3, and (b) 109/m3 . Find: R = ? µm where excess-water mixing ratio rE is in kgwater/ 3 Assume: ρwater = 1000 kg/m , as listed in Appendix A. kgair, ρ is density, and n is the number density of hydrometeors (the count of hydrometeors per cu- Use eq. (7.8). Part (a),: bic meter of air). Typical values are R = 2 to 50 µm, which is small compared to the 1000 µm separation 3 1/ 3 3·( 1kgair/m )·(.0 004kgwater/kg air ) between droplets, and is too small to be precipita- R = 3 38 -3 4π·( 10 kkg /m )·()10 m tion. water This is an important consideration. Namely, even if we ignore the slowness of the diffusion process = 2.12x10–5 m = 21.2 µm. (described later), the hydrometeors stop growing by condensation or deposition before they become (b) Similarly, R = 9.8 µm. precipitation. The reason is that there are too many hydrometeors, all competing for water molecules, Check: Units OK.
Load more

Recommended publications
  • Thermodynamics and Kinetics of Nucleation in Binary Solutions
    1 Thermodynamics and kinetics of nucleation in binary solutions Nikolay V. Alekseechkin Akhiezer Institute for Theoretical Physics, National Science Centre “Kharkov Institute of Physics and Technology”, Akademicheskaya Street 1, Kharkov 61108, Ukraine Email: [email protected] Keywords: Binary solution; phase equilibrium; binary nucleation; diffusion growth; surface layer. A new approach that is a combination of classical thermodynamics and macroscopic kinetics is offered for studying the nucleation kinetics in condensed binary solutions. The theory covers the separation of liquid and solid solutions proceeding along the nucleation mechanism, as well as liquid-solid transformations, e.g., the crystallization of molten alloys. The cases of nucleation of both unary and binary precipitates are considered. Equations of equilibrium for a critical nucleus are derived and then employed in the macroscopic equations of nucleus growth; the steady state nucleation rate is calculated with the use of these equations. The present approach can be applied to the general case of non-ideal solution; the calculations are performed on the model of regular solution within the classical nucleation theory (CNT) approximation implying the bulk properties of a nucleus and constant surface tension. The way of extending the theory beyond the CNT approximation is shown in the framework of the finite- thickness layer method. From equations of equilibrium of a surface layer with coexisting bulk phases, equations for adsorption and the dependences of surface tension on temperature, radius, and composition are derived. Surface effects on the thermodynamics and kinetics of nucleation are discussed. 1. Introduction Binary nucleation covers a wide class of processes of phase transformations which can be divided into three groups: (i) gas-liquid (or solid) transformations, (ii) liquid-gas transformations, and (iii) transformations within a condensed state.
    [Show full text]
  • Determination of Supercooling Degree, Nucleation and Growth Rates, and Particle Size for Ice Slurry Crystallization in Vacuum
    crystals Article Determination of Supercooling Degree, Nucleation and Growth Rates, and Particle Size for Ice Slurry Crystallization in Vacuum Xi Liu, Kunyu Zhuang, Shi Lin, Zheng Zhang and Xuelai Li * School of Chemical Engineering, Fuzhou University, Fuzhou 350116, China; [email protected] (X.L.); [email protected] (K.Z.); [email protected] (S.L.); [email protected] (Z.Z.) * Correspondence: [email protected] Academic Editors: Helmut Cölfen and Mei Pan Received: 7 April 2017; Accepted: 29 April 2017; Published: 5 May 2017 Abstract: Understanding the crystallization behavior of ice slurry under vacuum condition is important to the wide application of the vacuum method. In this study, we first measured the supercooling degree of the initiation of ice slurry formation under different stirring rates, cooling rates and ethylene glycol concentrations. Results indicate that the supercooling crystallization pressure difference increases with increasing cooling rate, while it decreases with increasing ethylene glycol concentration. The stirring rate has little influence on supercooling crystallization pressure difference. Second, the crystallization kinetics of ice crystals was conducted through batch cooling crystallization experiments based on the population balance equation. The equations of nucleation rate and growth rate were established in terms of power law kinetic expressions. Meanwhile, the influences of suspension density, stirring rate and supercooling degree on the process of nucleation and growth were studied. Third, the morphology of ice crystals in ice slurry was obtained using a microscopic observation system. It is found that the effect of stirring rate on ice crystal size is very small and the addition of ethylene glycoleffectively inhibits the growth of ice crystals.
    [Show full text]
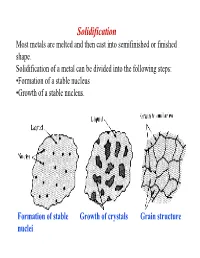
  • Solidification Most Metals Are Melted and Then Cast Into Semifinished Or Finished Shape
    Solidification Most metals are melted and then cast into semifinished or finished shape. Solidification of a metal can be divided into the following steps: •Formation of a stable nucleus •Growth of a stable nucleus. Formation of stable Growth of crystals Grain structure nuclei Polycrystalline Metals In most cases, solidification begins from multiple sites, each of which can produce a different orientation The result is a “polycrystalline” material consisting of many small crystals of “grains” Each grain has the same crystal lattice, but the lattices are misoriented from grain to grain Driving force: solidification ⇒ For the reaction to proceed to the right ∆G AL AS V must be negative. • Writing the free energies of the solid and liquid as: S S S GV = H - TS L L L GV = H - TS ∴∴∴ ∆GV = ∆H - T∆S • At equilibrium, i.e. Tmelt , then the ∆GV = 0 , so we can estimate the melting entropy as: ∆S = ∆H/Tmelt where -∆H is the latent heat (enthalpy) of melting. • Ignore the difference in specific heat between solid and liquid, and we estimate the free energy difference as: T ∆H × ∆T ∆GV ≅ ∆H − ∆H = TMelt TMelt NUCLEATION The two main mechanisms by which nucleation of a solid particles in liquid metal occurs are homogeneous and heterogeneous nucleation. Homogeneous Nucleation Homogeneous nucleation occurs when there are no special objects inside a phase which can cause nucleation. For instance when a pure liquid metal is slowly cooled below its equilibrium freezing temperature to a sufficient degree numerous homogeneous nuclei are created by slow-moving atoms bonding together in a crystalline form.
    [Show full text]
  • Nucleation Theory: a Literature Review and Applications to Nucleation Rates of Natural Gas Hydrates
    Nucleation Theory: A Literature Review and Applications to Nucleation Rates of Natural Gas Hydrates Simon Davies SUMMARY Predicting the onset of hydrate nucleation in oil pipelines is one of the most challenging aspects in the flow assurance modelling work being performed at the Center for Hydrate Research. Nucleation is initiated by a random fluctuation which is able to overcome the energy barrier for the phase transition, once such a fluctuation occurs, further growth is energetically favourable. Historically the random fluctuation requires for nucleation was defined as the formation of a nucleus of critical size. Recently, more realistic models have been proposed based on density functional theory. In this report, a literature survey of nucleation theory was performed in order to determine the state-of-the-art understanding of hydrate nucleation. A simplified nucleation model was then designed based on a two dimensional Ising model, in order to determine thermodynamic properties for nuclei of various sizes. The model used window sampling to collect high resolution statistics for the high energy states. It was demonstrated that the shape and height of the energy barrier can be determined for a nucleating system in this way. INTRODUCTION The ability to predict the onset of nucleation is important for a wide variety of first order phase transitions from industrial crystallisers to rainfall. Systems can be held in a supersaturated state for significant periods of time before a phase transition occurs: distilled water can be held indefinitely at -10ºC without freezing, with further purification it can be cooled to -30ºC without freezing [1]. Predicting the onset of hydrate nucleation in oil pipelines is one of the most challenging aspects in the flow assurance modelling work being performed at the Center for Hydrate Research.
    [Show full text]
  • Gas Supersaturation Thresholds for Spontaneous Cavitation in Water with Gas Equilibration Pressures up to 570 Atm1 Wayne A
    Gas Supersaturation Thresholds for Spontaneous Cavitation in Water with Gas Equilibration Pressures up to 570 atm1 Wayne A. Gerth and Edvard A. Hemmingsen * Physiological Research Laboratory Scripps Institution of Oceanography University of California, San Diego La Jolla, California 92093 (Z. Naturforsch. 31a, 1711-1716 [1976] ; received October 5, 1976) Supersaturations for the onset of cavitation in water were determined for various gases. At am- bient pressure, the threshold supersaturations (in atm) required for profuse cavitation to initiate both in bulk water and at the glass-water interface were CH4, 120; Ar, 160; N2, 190; He, 360. Exposure of the water and its containing surfaces to hydrostatic pressures up to 1100 atm prior to equilibration with gas had no detectable effect on these threshold values. This indicates that pre- formed gas nuclei are not significantly involved. Cavitation at the glass-water interface was investi- gated for CH4, Ar and N, saturations up to 570 atm. For 320 atm saturations, the threshold super- saturation was about one-half that for decompression directly to ambient pressure, and for 550 atm it was about one-third. These results indicate that the dissolved gas concentration is a critical factor limiting the spontaneous nucleation of bubbles in gas supersaturated liquids. Introduction thereby forcing the resolution of such dissolvable nuclei 4. Water that contains large gas supersaturations The results reported here bear directly upon the can remain stable with the absence of cavitation 2' 3. understanding of the gas supersaturated metastable However, as the gas supersaturation in the water is condition in pure liquids, the factors which limit it, increased, the system eventually fails to tolerate the and the characteristics of its degeneration via the supersaturation and bursts profusely with the for- nucleation and growth of bubbles.
    [Show full text]
  • Chapter 1 the Fundamentals of Bubble Formation in Water Treatment
    Chapter 1 The Fundamentals of Bubble Formation in Water Treatment Paolo Scardina and Marc Edwards1 Keywords: bubble, air binding, filters, nucleation, equilibrium, water treatment, headloss, filtration, gas transfer Abstract: Water utilities can experience problems from bubble formation during conventional treatment, including impaired particle settling, filter air binding, and measurement as false turbidity in filter effluent. Coagulation processes can cause supersaturation and bubble formation by converting bicarbonate alkalinity to carbon dioxide by acidification. A model was developed to predict the extent of bubble formation during coagulation which proved accurate, using an apparatus designed to physically measure the actual volume of bubble formation. Alum acted similar to hydrochloric acid for initializing bubble formation, and higher initial alkalinity, lower final solution pH, and increased mixing rate tended to increase bubble formation. Lastly, the protocol outlined in Standard Methods for predicting the degree of supersaturation was examined, and when compared to this work, the Standard Methods approach produces an error up to 16% for conditions found in water treatment. Introduction: Gas bubble formation is of established importance to divers and fish (i.e., the bends), carbonated beverages, solid liquid separation in mining, cavitation in pumps, gas transfer, stripping, and dissolved air flotation processes. Moreover, it is common knowledge that formation of gas bubbles in conventional sedimentation and filtration facilities is a significant nuisance at many utilities, because bubbles are believed to hinder sedimentation, cause headloss in filters through a phenomenon referred to as “air binding,” and measure as turbidity in effluents without posing a microbial hazard. Utilities have come to accept these problems, and to the knowledge of these authors there is currently no rigorous basis for predicting when such problems will occur or correcting them when they do.
    [Show full text]
  • Cloud Microphysics
    1. Microphysics of Clouds Changes in phase are basic to cloud microphysics. The possible changes are: vapor-liquid evaporation, condensation liquid-solid freezing, melting vapor-solid deposition, sublimation The changes from left to right correspond to increasing molecular order. These transitions don’t occur at thermodynamic equilibrium. There is a strong free en- ergy barrier that must be overcome for droplets to form. To form a droplet by condensation of vapor, surface tension must be overcome by a strong gradient of vapor pressure. This means that phase transitions don’t occur at es(1), or sat- uration over a plane surface of water. Even if a sample of moist air is cooled adiabatically to the equilibrium saturation point for bulk water, droplets should not be expected to form. In fact, water droplets do begin to condense in pure wa- ter vapor only when the relative humidity reaches several hundred percent! This is called Homogeneous Nucleation. The reason why cloud droplets are observed to form in the atmosphere when ascending air just reaches equilibrium saturation is because the atmosphere con- tains significant concentrations of particles of micron and sub-micron size which have an affinity for water. This is called Heterogeneous Nucleation. There are many types of condensation nuclei in the atmosphere. Some become wetted at RH less than 100% and account for haze. Larger condensation nuclei may grow to cloud droplet size. As moist air is cooled adiabatically and RH is close to 100 the hygroscopic CCN begin to serve as centers of condensation. If ascent con- tinues, there is supersaturation by cooling which is depleted by condensation on the nuclei.
    [Show full text]
  • Carbonate Chemistry
    CHAPTER 3 SOLUTION-MINERAL EQUILIBRIA PART 1: CARBONATES Carbonic acid and the carbonate minerals provide another good illustration of the use of equilibrium reasoning in geochemistry. Interactions among these compounds determine the conditions under which limestones and dolomites are fomied or dissolved, and likewise the conditions of formation of carbonate minerals as cements in soils and sandstones and as vein fillings. We start with some qualitative remarks about the most common of these substances, the carbonate of calcium, then go on to a more quantitative treatment and to the reactions of other common carbonate minerals. • 3-1 SOLUBILITY OF CALCITE Calcium carbonate occurs in nature as the two common minerals calcite and aragonite (Sec. 3-3). A third crystal form (vaterite) can be prepared artificially, and is known as a very rare mineral in nature. Under usual conditions near the Earth's surface calcite is the most stable and most abundant of the three forms, and for the discussion in this section and the next it will be the center of attention. Aragonite and vaterite may be assumed to show similar chemical behavior, but in general to react more rapidly and to have greater solubility. 61 62 INTRODUCTION TO GEOCHEMISTRY A strong acid dissolves calcite by the familiar reaction CaC03 + 2H+ ---+ Ca2+ + H20 + C02. (3-1 ) calcite At low acid concentrations a more accurate equation would be CaC03 + H+ - • Ca2+ + HCO) (3-2) calcite showing that W takes co~ - away from Ca2+ to form the very weak (little dissociated) acid HCO:J. (Still greater accuracy would require consideration of the complex ion CaHCOj , but under usual conditions its concentration is small and for the present can be neglected.) These reactions would take place in nature, for example, where acid solutions from the weathering of pyrite encounter limestone.
    [Show full text]
  • The Role of Evolving Surface Tension in the Formation of Cloud Droplets James F
    Technical Note: The Role of Evolving Surface Tension in the Formation of Cloud Droplets James F. Davies1, Andreas Zuend2, Kevin R. Wilson3 1Department of Chemistry, University of California Riverside, CA USA 5 2Department of Atmospheric and Oceanic Sciences, McGill University, Montreal, Quebec, Canada 3Chemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA USA Correspondence to: James F. Davies ([email protected]) Abstract. The role of surface tension (σ) in cloud droplet activation has long been ambiguous. Recent studies have reported observations attributed to the effects of an evolving surface tension in the activation 10 process. However, adoption of a surface-mediated activation mechanism has been slow and many studies continue to neglect the composition-dependence of aerosol/droplet surface tension, using instead a value equal to the surface tension of pure water (σw). In this technical note, we clearly describe the fundamental role of surface tension in the activation of multicomponent aerosol particles into cloud droplets. It is demonstrated that the effects of surface tension in the activation process depend primarily on the evolution 15 of surface tension with droplet size, typically varying in the range 0.5σw ≲ σ ≤ σw due to the partitioning of organic species with a high surface affinity. We go on to report some recent laboratory observations that exhibit behavior that may be associated with surface tension effects, and propose a measurement coordinate that will allow surface tension effects to be better identified using standard atmospheric measurement techniques. Unfortunately, interpreting observations using theory based on surface film and liquid-liquid 20 phase separation models remains a challenge.
    [Show full text]
  • Solid-Liquid Phase Equilibria and Crystallization of Disubstituted Benzene Derivatives
    Royal Institute of Technology School of Chemical Science and Engineering Department of Chemical Engineering and Technology Division of Transport Phenomena Solid-Liquid Phase Equilibria and Crystallization of Disubstituted Benzene Derivatives Fredrik Nordström Doctoral Thesis Akademisk avhandling som med tillstånd av Kungliga Tekniska Högskolan i Stockholm framlägges till offentlig granskning för avläggande av teknologie doktorsexamen den 30:e Maj 2008, kl. 10:00 i sal D3, Lindstedtsvägen 5, Stockholm. Avhandlingen försvaras på engelska. i Cover picture: Crystals of o-hydroxybenzoic acid (salicylic acid) obtained through evaporation crystallization in solutions of ethyl acetate at around room temperature. Solid-Liquid Phase Equilibria and Crystallization of Disubstituted Benzene Derivatives Doctoral Thesis © Fredrik L. Nordström, 2008 TRITA-CHE Report 2008-32 ISSN 1654-1081 ISBN 978-91-7178-949-5 KTH, Royal Institute of Technology School of Chemical Science and Engineering Department of Chemical Engineering and Technology Division of Transport Phenomena SE-100 44 Stockholm Sweden Paper I: Copyright © 2006 by Wiley InterScience Paper II: Copyright © 2006 by Elsevier Science Paper III: Copyright © 2006 by the American Chemical Society Paper IV: Copyright © 2006 by the American Chemical Society ii In loving memory of my grandparents Aina & Vilmar Nordström iii i v Abstract The Ph.D. project compiled in this thesis has focused on the role of the solvent in solid-liquid phase equilibria and in nucleation kinetics. Six organic substances have been selected as model compounds, viz. ortho-, meta- and para-hydroxybenzoic acid, salicylamide, meta- and para-aminobenzoic acid. The different types of crystal phases of these compounds have been explored, and their respective solid-state properties have been determined experimentally.
    [Show full text]
  • Crystallization of Supercooled Liquid Elements Induced by Superclusters Containing Magic Atom Numbers Robert F
    Crystallization of Supercooled Liquid Elements Induced by Superclusters Containing Magic Atom Numbers Robert F. Tournier, CRETA /CNRS, Université Joseph Fourier, B.P. 166, 38042 Grenoble cedex 09, France. E-mail: [email protected]; Tel.: +33-608-716-878; Fax: +33-956-705-473. Abstract: A few experiments have detected icosahedral superclusters in undercooled liquids. These superclusters survive above the crystal melting temperature Tm because all their surface atoms have the same fusion heat as their core atoms and are melted by liquid homogeneous and heterogeneous nucleation in their core, depending on superheating time and temperature. They act as heterogeneous growth nuclei of crystallized phase at a temperature Tc of the undercooled melt. They contribute to the critical barrier reduction, which becomes smaller than that of crystals containing the same atom number n. After strong superheating, the undercooling rate is still limited because the nucleation of 13-atom superclusters always reduces this barrier, and increases Tc above a homogeneous nucleation temperature equal to Tm/3 in liquid elements. After weak superheating, the most stable superclusters containing n = 13, 55, 147, 309 and 561 atoms survive or melt and determine Tc during undercooling, depending on n and sample volume. The experimental nucleation temperatures Tc of 32 liquid elements and the supercluster melting temperatures are predicted with sample volumes varying by 18 orders of magnitude. The classical Gibbs free energy change is used, adding an enthalpy saving related to the Laplace pressure change associated with supercluster formation, which is quantified for n=13 and 55. Keywords: thermal properties, solid-liquid interface energy, crystal nucleation, undercooling, superclusters, liquid-solid transition, overheating, non-metal to metal transition in cluster, Laplace pressure 1.
    [Show full text]
  • Microbubble Treatment of Gas Supersaturated Water
    MICROBUBBLE TREATMENT OF GAS SUPERSATURATED WATER Contract No. GS-23F-0339K/01PE810319 Desalination and Water Purification R&D Program Report No. 70 December 2001 U.S. Department of Interior Bureau of Reclamation Denver Office Technical Service Center Environmental Resources Team Water Treatment Engineering and Research Group MICROBUBBLE TREATMENT OF GAS SUPERSATURATED WATER Mark A. Lichtwardt ARCADIS G&M, Inc. Highlands Ranch, Colorado Co-Author Andrew Murphy Bureau of Reclamation Denver, Colorado Contract No. GS-23F-0339K/01PE810319 Desalination and Water Purification R&D Program Report No. 70 December 2001 U.S. Department of Interior Bureau of Reclamation Denver Office Technical Service Center Environmental Resources Team Water Treatment Engineering and Research Group Mission Statements U.S. Department of the Interior The mission of the Department of the Interior is to protect and provide access to our Nation’s natural and cultural heritage and honor our trust responsibilities to tribes. Bureau of Reclamation The mission of the Bureau of Reclamation is to manage, develop, and protect water and related resources in an environmentally and economically sound manner in the interest of the American public. Disclaimer The information contained in this report regarding commercial products or firms may not be used for advertising or promotional purposes and is not to be construed as an endorsement of any product or firm by the Bureau of Reclamation. The information contained in this report was developed for the Bureau of Reclamation; no warranty as to the accuracy, usefulness, or completeness is expressed or implied. Acknowledgements This work was financially supported by the U.S. Department of Interior, Bureau of Reclamation under Contract No.
    [Show full text]