DOCSLIB.ORG

Extreme Liquid Superheating and Homogeneous Bubble Nucleation in a Solid State Nanopore

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Extreme Liquid Superheating and Homogeneous Bubble Nucleation in a Solid State Nanopore Extreme Liquid Superheating and Homogeneous Bubble Nucleation in a Solid State Nanopore The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Levine, Edlyn Victoria. 2016. Extreme Liquid Superheating and Homogeneous Bubble Nucleation in a Solid State Nanopore. Doctoral dissertation, Harvard University, Graduate School of Arts & Sciences. Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:33493497 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Other Posted Material, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#LAA Extreme Liquid Superheating and Homogeneous Bubble Nucleation in a Solid State Nanopore a dissertation presented by Edlyn Victoria Levine to The School of Engineering and Applied Sciences in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the subject of Applied Physics Harvard University Cambridge, Massachusetts April 2016 ©2016 – Edlyn Victoria Levine all rights reserved. Thesis advisor: Professor Jene A. Golovchenko Author: Edlyn Victoria Levine Extreme Liquid Superheating and Homogeneous Bubble Nucleation in a Solid State Nanopore Abstract This thesis explains how extreme superheating and single bubble nucleation can be achieved in an electrolytic solution within a solid state nanopore. A highly focused ionic current, induced to flow through the pore by modest voltage biases, leads to rapid Joule heating of the electrolyte in the nanopore. At sufficiently high current densities, temperatures near the thermodynamic limit of superheat are achieved, ultimately leading to nucleation of a vapor bubble within the nanopore. A mathematical model for Joule heating of an electrolytic solution within a nanopore is presented. This model couples the electrical and thermal dynamics responsible for rapid and extreme superheating of the electrolyte within the nanopore. The model is implemented nu- merically with a finite element calculation, yielding a time and spatially resolved temperature distribution in the nanopore region. Temperatures near the thermodynamic limit of superheat are predicted to be attained just before the explosive nucleation of a vapor bubble is observed experimentally. Knowledge of this temperature distribution is used to evaluate related phenomena including bubble nucleation kinetics, relaxation oscillation, and bubble dynamics. In particular, bubble nucleation is shown to be homogeneous and highly reproducible. These results are consistent with experimental data available from electronic and optical measurements of Joule heating and bubble nucleation in a nanopore. iii Contents Abstract iii Table of Contents v List of Figures vii Dedication viii Acknowledgments ix 1 Introduction 1 1.1 Solid State Nanopores ............................... 3 1.2 Experimental Investigation of Joule Heating in a Nanopore ........... 3 1.3 The Superheated Liquid: A State of Metastable Equilibrium ........... 7 1.4 Organization of Thesis ............................... 14 2 The Dynamics of Joule Heating in a Solid State Nanopore 17 2.1 Aqueous 3M Sodium Chloride Solution ...................... 18 2.2 Electrodiffusion of Ions: Applying a Voltage Bias to the Electrolyte . 23 2.3 Electroosmotic Flow and the Convection of Ions . 26 2.4 Entropy Balance of Thermoelectric Phenomena . 27 2.5 Summary of Governing Equations ......................... 39 3 Model of Joule Heating in a Nanopore: Finite Element Method (FEM) 41 3.1 Simplifying the Governing Equations ....................... 42 3.2 Geometry and Boundary Conditions of the Nanopore System . 45 3.3 Material Properties ................................. 47 3.4 Numerical Implementation: Meshing and Solvers . 49 4 FEM Model Results and Discussion 51 4.1 Electrical Conductivity of the Superheated Electrolyte . 52 iv 4.2 Extreme Superheating within the Nanopore .................... 55 4.3 Comparison with the Limit of Superheat of Pure Water . 57 4.4 Induced Charge Densities Near the Nanopore ................... 59 5 Analytical Approaches to the Joule Heating Problem 61 5.1 Dimensionless Form of the Governing Equations for a Simplified Model . 62 5.2 Green’s Function Solution ............................. 66 5.3 Comparison of Analytical Solution with Numerical Results . 74 5.4 Remarks in Summary ............................... 76 6 Kinetics of Bubble Nucleation in the Nanopore 78 6.1 Surface Tension and the Size of the Critical Nucleus . 79 6.2 Fluctuations Driving Bubble Nucleation ..................... 84 6.3 The Kinetics of Phase Transformation ....................... 88 6.4 Homogeneous Nucleation of the Vapor Bubble in the Nanopore . 92 6.5 Heterogeneous Nucleation ............................. 95 6.6 Experimental Confirmation of Homogeneous Nucleation . 95 7 Temperature and Bubble Dynamics in the Nanopore After Nucleation 100 7.1 Dynamics of Heating and Relaxation Oscillation . 102 7.2 The Equations Governing Bubble Dynamics . 104 7.3 Approximating the Initial Growth of the Bubble . 109 7.4 Exploring the Complete Bubble Dynamics . 111 8 Conclusion 113 8.1 Summary of Results Presented in this Thesis . 114 8.2 The Future for Joule Heating in Nanopores . 115 Appendix A The Debye-Huckel¨ Theory 117 Appendix B Equations of Continuity and Conservation 125 Appendix C Solution of Joule Heating with Separation of Variables 141 Appendix D From Navier-Stokes to Rayleigh-Plesset 152 References 167 v Listing of figures 1.1 Experimental Setup: Conductance Measurement ................. 4 1.2 Experimental Results: Nanopore Conductance .................. 5 1.3 Experimental Results: Nucleation Events ..................... 6 1.4 PV Diagram, van der Waals Fluid ......................... 9 1.5 Gibbs free energy, van der Waals Fluid ...................... 11 1.6 PT Diagram, van der Waals Fluid ......................... 13 2.1 Debye Length for NaCl Solutions of Different Conductivities . 22 3.1 Nanopore Geometry for FEM Model ....................... 46 3.2 Temperature Dependence of the Material Properties of H2O . 48 4.1 Temperature Dependence of the Electrical Conductivity, 3M NaCl . 53 4.2 Nanopore Conductance, Data and Fit ....................... 54 4.3 Temperature Distribution in the Nanopore .................... 56 4.4 Maximum Temperature in the Nanopore ..................... 57 4.5 Charge Densities In and Near the Nanopore .................... 60 5.1 Radial Green’s Function vs Time ......................... 71 5.2 Radial Green’s Function vs Radius ........................ 72 5.3 Temperature Distribution from Green’s Function Method . 73 5.4 Analytical and Finite Element: T vs r ....................... 74 5.5 Analytical and Finite Element: T vs t ....................... 75 5.6 Joule Heating Source Term ............................ 76 6.1 Temperature Dependence of Surface Tension ................... 82 6.2 Temperature Dependence of Critical Radius ................... 83 6.3 Energetic Barrier to Nucleation .......................... 86 6.4 Nucleation Rate as a Function of T ........................ 92 6.5 Nanopore Conductance and Bubble Nucleation . 93 vi 6.6 Nucleation Rate Inside the Nanopore ....................... 94 6.7 Optical Experimental Setup ............................ 96 6.8 Optical Transmission Data ............................. 97 6.9 Homogeneous Nucleation: Delay between Ionic and Photodiode Current . 98 7.1 Experimental Results: Nucleation Events . 101 7.2 Temperature Dynamics of Relaxation Oscillation: Maximum Temperature . 102 7.3 Temperature Dynamics of Relaxation Oscillation: Spatial Distribution . 103 7.4 Rayleigh-Plesset Dynamics of Bubble Growth . 110 C.1 Analytical Solution for Temperature Distribution . 149 vii To my parents viii Acknowledgments Achievements are not attained in isolation, and I can thankfully say this is true for my the- sis. I have had the great fortune of having supportive family, friends, and mentors who have contributed to my growth and indeed to the development of this work. I am particularly grateful to my parents, Drs. Barry and Arlene Levine, and to my brother, Lionel, for their loving and caring support throughout my life. Thank you for cheering me on in all my diverse and various endeavors, both in physics, and in other aspects of life. I would like to thank my advisor, Prof. Jene Golovchenko for his guidance and mentorship throughout my time in graduate school, and for fostering my development as a physicist. Many thanks as well to Dr. Mike Burns and Prof. Lene Hau for consistent advice and feedback. I would like to give credit to Gaku Nagashima for conducting all of the experiments I discuss in this work, and am thankful to him for his friendship over the years. I am also grateful to Dr. David Hoogerheide, Aaron Kuan, Tamas Szalay, Dr. Ryan Rollings, Dr. Lu Bo, Don Dressen and Stephen Flemings for many interesting discussions about physics and of course, conversations about life in general. Finally, I want to thank Eric Brandin, Peter Frisella, Ray Aubut, and Jane Salant for everything they have done in support of this research. ix The single, all-encompassing problem of thermody- namics is the determination of the equilibrium state that eventually results after the removal of internal constraints in a closed, composite system. Herbert B. Callen 1 Introduction We recently discovered that an aqueous electrolyte can be strongly superheated within a solid- state nanopore by electrical
Load more

Recommended publications
  • Parallel-Powered Hybrid Cycle with Superheating “Partially” by Gas
    Parallel-Powered Hybrid Cycle with Superheating “Partially” by Gas Turbine Exhaust Milad Ghasemi, Hassan Hammodi, Homan Moosavi Sigaroodi ETA800 Final Thesis Project Division of Heat and Power Technology Department of Energy Technology Royal Institute of Technology Stockholm, Sweden [This page is left intentionally blank for the purposes of printing] Abstract It is of great importance to acquire methods that has a sustainable solution for treatment and disposal of municipal solid waste (MSW). The volumes are constantly increasing and improper waste management, like open dumping and landfilling, causes environmental impacts such as groundwater contamination and greenhouse gas emissions. The rationalization of developing a sustainable solution implies in an improved way of utilizing waste resources as an energy source with highest possible efficiency. MSW incineration is by far the best available way to dispose the waste. One drawback of conventional MSW incineration plants is that when the energy recovery occurs in the steam power cycle configuration, the reachable efficiency is limited due to steam parameters. The corrosive problem limits the temperature of the superheated steam from the boiler which lowers the efficiency of the system. A suitable and relatively cheap option for improving the efficiency of the steam power cycle is the implementation of a hybrid dual-fuel cycle. This paper aims to assess the integration of an MSW incineration with a high quality fuel conversion device, in this case natural gas (NG) combustion cycle, in a hybrid cycle. The aforementioned hybrid dual-fuel configuration combines a gas turbine topping cycle (TC) and a steam turbine bottoming cycle (BC). The TC utilizes the high quality fuel NG, while the BC uses the lower quality fuel, MSW, and reaches a total power output of 50 MW.
    [Show full text]
  • Physics, Chapter 17: the Phases of Matter
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Robert Katz Publications Research Papers in Physics and Astronomy 1-1958 Physics, Chapter 17: The Phases of Matter Henry Semat City College of New York Robert Katz University of Nebraska-Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/physicskatz Part of the Physics Commons Semat, Henry and Katz, Robert, "Physics, Chapter 17: The Phases of Matter" (1958). Robert Katz Publications. 165. https://digitalcommons.unl.edu/physicskatz/165 This Article is brought to you for free and open access by the Research Papers in Physics and Astronomy at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Robert Katz Publications by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. 17 The Phases of Matter 17-1 Phases of a Substance A substance which has a definite chemical composition can exist in one or more phases, such as the vapor phase, the liquid phase, or the solid phase. When two or more such phases are in equilibrium at any given temperature and pressure, there are always surfaces of separation between the two phases. In the solid phase a pure substance generally exhibits a well-defined crystal structure in which the atoms or molecules of the substance are arranged in a repetitive lattice. Many substances are known to exist in several different solid phases at different conditions of temperature and pressure. These solid phases differ in their crystal structure. Thus ice is known to have six different solid phases, while sulphur has four different solid phases.
    [Show full text]
  • Thermodynamics and Kinetics of Nucleation in Binary Solutions
    1 Thermodynamics and kinetics of nucleation in binary solutions Nikolay V. Alekseechkin Akhiezer Institute for Theoretical Physics, National Science Centre “Kharkov Institute of Physics and Technology”, Akademicheskaya Street 1, Kharkov 61108, Ukraine Email: [email protected] Keywords: Binary solution; phase equilibrium; binary nucleation; diffusion growth; surface layer. A new approach that is a combination of classical thermodynamics and macroscopic kinetics is offered for studying the nucleation kinetics in condensed binary solutions. The theory covers the separation of liquid and solid solutions proceeding along the nucleation mechanism, as well as liquid-solid transformations, e.g., the crystallization of molten alloys. The cases of nucleation of both unary and binary precipitates are considered. Equations of equilibrium for a critical nucleus are derived and then employed in the macroscopic equations of nucleus growth; the steady state nucleation rate is calculated with the use of these equations. The present approach can be applied to the general case of non-ideal solution; the calculations are performed on the model of regular solution within the classical nucleation theory (CNT) approximation implying the bulk properties of a nucleus and constant surface tension. The way of extending the theory beyond the CNT approximation is shown in the framework of the finite- thickness layer method. From equations of equilibrium of a surface layer with coexisting bulk phases, equations for adsorption and the dependences of surface tension on temperature, radius, and composition are derived. Surface effects on the thermodynamics and kinetics of nucleation are discussed. 1. Introduction Binary nucleation covers a wide class of processes of phase transformations which can be divided into three groups: (i) gas-liquid (or solid) transformations, (ii) liquid-gas transformations, and (iii) transformations within a condensed state.
    [Show full text]
  • Thermodynamics of Air-Vapour Mixtures Module A
    roJuclear Reactor Containment Design Chapter 4: Thermodynamics ofAir-Vapour Mixtures Dr. Johanna Daams page 4A - 1 Module A: Introduction to Modelling CHAPTER 4: THERMODYNAMICS OF AIR-VAPOUR MIXTURES MODULE A: INTRODUCTION TO MODELLING MODULE OBJECTIVES: At the end of this module, you will be able to describe: 1. The three types of modelling, required for nuclear stations 2. The differences between safety code, training simulator code and engineering code ,... --, Vuclear Reector Conte/nment Design Chapter 4: Thermodynamics ofAir-Vapour Mixtures ". Johanna Daams page 4A-2 Module A: Introduction to Modelling 1.0 TYPES OF MODELLING CODE n the discussion of mathematical modelling of containment that follows, I will often say that certain !pproxlmatlons are allowable for simple simulations, and that safety analysis require more elaborate :alculations. Must therefore understand requirements for different types of simulation. 1.1 Simulation for engineering (design and post-construction design changes): • Purpose: Initially confirm system is within design parameters • limited scope - only parts of plant, few scenarios - and detail; • Simplified representation of overall plant or of a system to design feedback loops 1.2 Simulation for safety analysis: • Purpose: confirm that the nuclear station's design and operation during normal and emergency conditions will not lead to unacceptable excursions in physical parameters leading to equipment failure and risk to the public. Necessary to license plant design and operating mode. • Scope: all situations that may cause unsafe conditions. All systems that may cause such conditions. • Very complex representation of components and physical processes that could lead to public risk • Multiple independent programs for different systems, e.g.
    [Show full text]
  • Determination of Supercooling Degree, Nucleation and Growth Rates, and Particle Size for Ice Slurry Crystallization in Vacuum
    crystals Article Determination of Supercooling Degree, Nucleation and Growth Rates, and Particle Size for Ice Slurry Crystallization in Vacuum Xi Liu, Kunyu Zhuang, Shi Lin, Zheng Zhang and Xuelai Li * School of Chemical Engineering, Fuzhou University, Fuzhou 350116, China; [email protected] (X.L.); [email protected] (K.Z.); [email protected] (S.L.); [email protected] (Z.Z.) * Correspondence: [email protected] Academic Editors: Helmut Cölfen and Mei Pan Received: 7 April 2017; Accepted: 29 April 2017; Published: 5 May 2017 Abstract: Understanding the crystallization behavior of ice slurry under vacuum condition is important to the wide application of the vacuum method. In this study, we first measured the supercooling degree of the initiation of ice slurry formation under different stirring rates, cooling rates and ethylene glycol concentrations. Results indicate that the supercooling crystallization pressure difference increases with increasing cooling rate, while it decreases with increasing ethylene glycol concentration. The stirring rate has little influence on supercooling crystallization pressure difference. Second, the crystallization kinetics of ice crystals was conducted through batch cooling crystallization experiments based on the population balance equation. The equations of nucleation rate and growth rate were established in terms of power law kinetic expressions. Meanwhile, the influences of suspension density, stirring rate and supercooling degree on the process of nucleation and growth were studied. Third, the morphology of ice crystals in ice slurry was obtained using a microscopic observation system. It is found that the effect of stirring rate on ice crystal size is very small and the addition of ethylene glycoleffectively inhibits the growth of ice crystals.
    [Show full text]
  • Structural Transformation in Supercooled Water Controls the Crystallization Rate of Ice
    Structural transformation in supercooled water controls the crystallization rate of ice. Emily B. Moore and Valeria Molinero* Department of Chemistry, University of Utah, Salt Lake City, UT 84112-0580, USA. Contact Information for the Corresponding Author: VALERIA MOLINERO Department of Chemistry, University of Utah 315 South 1400 East, Rm 2020 Salt Lake City, UT 84112-0850 Phone: (801) 585-9618; fax (801)-581-4353 Email: [email protected] 1 One of water’s unsolved puzzles is the question of what determines the lowest temperature to which it can be cooled before freezing to ice. The supercooled liquid has been probed experimentally to near the homogeneous nucleation temperature T H≈232 K, yet the mechanism of ice crystallization—including the size and structure of critical nuclei—has not yet been resolved. The heat capacity and compressibility of liquid water anomalously increase upon moving into the supercooled region according to a power law that would diverge at T s≈225 K,1,2 so there may be a link between water’s thermodynamic anomalies and the crystallization rate of ice. But probing this link is challenging because fast crystallization prevents experimental studies of the liquid below T H. And while atomistic studies have captured water crystallization3, the computational costs involved have so far prevented an assessment of the rates and mechanism involved. Here we report coarse-grained molecular simulations with the mW water model4 in the supercooled regime around T H, which reveal that a sharp increase in the fraction of four-coordinated molecules in supercooled liquid water explains its anomalous thermodynamics and also controls the rate and mechanism of ice formation.
    [Show full text]
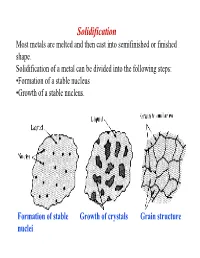
  • Solidification Most Metals Are Melted and Then Cast Into Semifinished Or Finished Shape
    Solidification Most metals are melted and then cast into semifinished or finished shape. Solidification of a metal can be divided into the following steps: •Formation of a stable nucleus •Growth of a stable nucleus. Formation of stable Growth of crystals Grain structure nuclei Polycrystalline Metals In most cases, solidification begins from multiple sites, each of which can produce a different orientation The result is a “polycrystalline” material consisting of many small crystals of “grains” Each grain has the same crystal lattice, but the lattices are misoriented from grain to grain Driving force: solidification ⇒ For the reaction to proceed to the right ∆G AL AS V must be negative. • Writing the free energies of the solid and liquid as: S S S GV = H - TS L L L GV = H - TS ∴∴∴ ∆GV = ∆H - T∆S • At equilibrium, i.e. Tmelt , then the ∆GV = 0 , so we can estimate the melting entropy as: ∆S = ∆H/Tmelt where -∆H is the latent heat (enthalpy) of melting. • Ignore the difference in specific heat between solid and liquid, and we estimate the free energy difference as: T ∆H × ∆T ∆GV ≅ ∆H − ∆H = TMelt TMelt NUCLEATION The two main mechanisms by which nucleation of a solid particles in liquid metal occurs are homogeneous and heterogeneous nucleation. Homogeneous Nucleation Homogeneous nucleation occurs when there are no special objects inside a phase which can cause nucleation. For instance when a pure liquid metal is slowly cooled below its equilibrium freezing temperature to a sufficient degree numerous homogeneous nuclei are created by slow-moving atoms bonding together in a crystalline form.
    [Show full text]
  • TABLE A-2 Properties of Saturated Water (Liquid–Vapor): Temperature Table Specific Volume Internal Energy Enthalpy Entropy # M3/Kg Kj/Kg Kj/Kg Kj/Kg K Sat
    720 Tables in SI Units TABLE A-2 Properties of Saturated Water (Liquid–Vapor): Temperature Table Specific Volume Internal Energy Enthalpy Entropy # m3/kg kJ/kg kJ/kg kJ/kg K Sat. Sat. Sat. Sat. Sat. Sat. Sat. Sat. Temp. Press. Liquid Vapor Liquid Vapor Liquid Evap. Vapor Liquid Vapor Temp. Њ v ϫ 3 v Њ C bar f 10 g uf ug hf hfg hg sf sg C O 2 .01 0.00611 1.0002 206.136 0.00 2375.3 0.01 2501.3 2501.4 0.0000 9.1562 .01 H 4 0.00813 1.0001 157.232 16.77 2380.9 16.78 2491.9 2508.7 0.0610 9.0514 4 5 0.00872 1.0001 147.120 20.97 2382.3 20.98 2489.6 2510.6 0.0761 9.0257 5 6 0.00935 1.0001 137.734 25.19 2383.6 25.20 2487.2 2512.4 0.0912 9.0003 6 8 0.01072 1.0002 120.917 33.59 2386.4 33.60 2482.5 2516.1 0.1212 8.9501 8 10 0.01228 1.0004 106.379 42.00 2389.2 42.01 2477.7 2519.8 0.1510 8.9008 10 11 0.01312 1.0004 99.857 46.20 2390.5 46.20 2475.4 2521.6 0.1658 8.8765 11 12 0.01402 1.0005 93.784 50.41 2391.9 50.41 2473.0 2523.4 0.1806 8.8524 12 13 0.01497 1.0007 88.124 54.60 2393.3 54.60 2470.7 2525.3 0.1953 8.8285 13 14 0.01598 1.0008 82.848 58.79 2394.7 58.80 2468.3 2527.1 0.2099 8.8048 14 15 0.01705 1.0009 77.926 62.99 2396.1 62.99 2465.9 2528.9 0.2245 8.7814 15 16 0.01818 1.0011 73.333 67.18 2397.4 67.19 2463.6 2530.8 0.2390 8.7582 16 17 0.01938 1.0012 69.044 71.38 2398.8 71.38 2461.2 2532.6 0.2535 8.7351 17 18 0.02064 1.0014 65.038 75.57 2400.2 75.58 2458.8 2534.4 0.2679 8.7123 18 19 0.02198 1.0016 61.293 79.76 2401.6 79.77 2456.5 2536.2 0.2823 8.6897 19 20 0.02339 1.0018 57.791 83.95 2402.9 83.96 2454.1 2538.1 0.2966 8.6672 20 21 0.02487 1.0020
    [Show full text]
  • Spinodal Lines and Equations of State: a Review
    10 l Nuclear Engineering and Design 95 (1986) 297-314 297 North-Holland, Amsterdam SPINODAL LINES AND EQUATIONS OF STATE: A REVIEW John H. LIENHARD, N, SHAMSUNDAR and PaulO, BINEY * Heat Transfer/ Phase-Change Laboratory, Mechanical Engineering Department, University of Houston, Houston, TX 77004, USA The importance of knowing superheated liquid properties, and of locating the liquid spinodal line, is discussed, The measurement and prediction of the spinodal line, and the limits of isentropic pressure undershoot, are reviewed, Means are presented for formulating equations of state and fundamental equations to predict superheated liquid properties and spinodal limits, It is shown how the temperature dependence of surface tension can be used to verify p - v - T equations of state, or how this dependence can be predicted if the equation of state is known. 1. Scope methods for making simplified predictions of property information, which can be applied to the full range of Today's technology, with its emphasis on miniaturiz­ fluids - water, mercury, nitrogen, etc. [3-5]; and predic­ ing and intensifying thennal processes, steadily de­ tions of the depressurizations that might occur in ther­ mands higher heat fluxes and poses greater dangers of mohydraulic accidents. (See e.g. refs. [6,7].) sending liquids beyond their boiling points into the metastable, or superheated, state. This state poses the threat of serious thermohydraulic explosions. Yet we 2. The spinodal limit of liquid superheat know little about its thermal properties, and cannot predict process behavior after a liquid becomes super­ heated. Some of the practical situations that require a 2.1. The role of the equation of state in defining the spinodal line knowledge the limits of liquid superheat, and the physi­ cal properties of superheated liquids, include: - Thennohydraulic explosions as might occur in nuclear Fig.
    [Show full text]
  • Subcritical Water Extraction
    Chapter 17 Subcritical Water Extraction A. Haghighi Asl and M. Khajenoori Additional information is available at the end of the chapter http://dx.doi.org/10.5772/54993 1. Introduction Extraction always involves a chemical mass transfer from one phase to another. The principles of extraction are used to advantage in everyday life, for example in making juices, coffee and others. To reduce the use of organic solvent and improve the extraction methods of constituents of plant materials, new methods such as microwave assisted extraction (MAE), supercritical fluid extraction (SFE), accelerated solvent extraction (ASE) or pressurized liquid extraction (PLE) and subcritical water extraction (SWE), also called superheated water extraction or pressurized hot water extraction (PHWE), have been introduced [1-3]. SWE is a new and powerful technique at temperatures between 100 and 374oC and pressure high enough to maintain the liquid state (Fig.1) [4]. Unique properties of water are namely its disproportionately high boiling point for its mass, a high dielectric constant and high polarity [4]. As the temperature rises, there is a marked and systematic decrease in permittivity, an increase in the diffusion rate and a decrease in the viscosity and surface tension. In conse‐ quence, more polar target materials with high solubility in water at ambient conditions are extracted most efficiently at lower temperatures, whereas moderately polar and non-polar targets require a less polar medium induced by elevated temperature [5]. Based on the research works published in the recent years, it has been shown that the SWE is cleaner, faster and cheaper than the conventional extraction methods.
    [Show full text]
  • Nucleation Theory: a Literature Review and Applications to Nucleation Rates of Natural Gas Hydrates
    Nucleation Theory: A Literature Review and Applications to Nucleation Rates of Natural Gas Hydrates Simon Davies SUMMARY Predicting the onset of hydrate nucleation in oil pipelines is one of the most challenging aspects in the flow assurance modelling work being performed at the Center for Hydrate Research. Nucleation is initiated by a random fluctuation which is able to overcome the energy barrier for the phase transition, once such a fluctuation occurs, further growth is energetically favourable. Historically the random fluctuation requires for nucleation was defined as the formation of a nucleus of critical size. Recently, more realistic models have been proposed based on density functional theory. In this report, a literature survey of nucleation theory was performed in order to determine the state-of-the-art understanding of hydrate nucleation. A simplified nucleation model was then designed based on a two dimensional Ising model, in order to determine thermodynamic properties for nuclei of various sizes. The model used window sampling to collect high resolution statistics for the high energy states. It was demonstrated that the shape and height of the energy barrier can be determined for a nucleating system in this way. INTRODUCTION The ability to predict the onset of nucleation is important for a wide variety of first order phase transitions from industrial crystallisers to rainfall. Systems can be held in a supersaturated state for significant periods of time before a phase transition occurs: distilled water can be held indefinitely at -10ºC without freezing, with further purification it can be cooled to -30ºC without freezing [1]. Predicting the onset of hydrate nucleation in oil pipelines is one of the most challenging aspects in the flow assurance modelling work being performed at the Center for Hydrate Research.
    [Show full text]
  • Source Term Models for Superheated Releases of Hazardous Materials
    Source Term Models for Superheated Releases of Hazardous Materials Thesis submitted for the Degree of Doctor of Philosophy of the University of Wales Cardiff by Vincent Martin Cleary BEng (Hons) September 2008 UMI Number: U585126 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a complete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. Dissertation Publishing UMI U585126 Published by ProQuest LLC 2013. Copyright in the Dissertation held by the Author. Microform Edition © ProQuest LLC. All rights reserved. This work is protected against unauthorized copying under Title 17, United States Code. ProQuest LLC 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106-1346 Chapter 1 Introduction Abstract Source terms models for superheated releases of hazardous liquefied chemicals such as LPG have been developed, governing both upstream and downstream conditions. Water was utilised as the model fluid, not least for reasons of safety, but also for its ability to be stored at conditions that ensure it is superheated on release to atmosphere. Several studies have found that at low superheat jet break-up is analogous to mechanical break-up under sub-cooled conditions. Hence, a non-dimensionalised SMD correlation for sub-cooled liquid jets in the atomisation regime has been developed, based on data measured using a Phase Doppler Anemometry (PDA) system, for a broad range of initial conditions. Droplet SMD has been found to correlate with the nozzle aspect ratio and two non- dimensionalised groups i.e.
    [Show full text]