DOCSLIB.ORG

Optical Properties of Terrestrial Clouds

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Optical Properties of Terrestrial Clouds Earth-Science Reviews 64 (2004) 189–241 www.elsevier.com/locate/earscirev Optical properties of terrestrial clouds A. Kokhanovsky* Institute of Environmental Physics, University of Bremen, Otto Hahn Allee 1, D-28334 Bremen, Germany Institute of Physics, 70 Skarina Avenue, Minsk 220072, Belarus Received 18 January 2002; accepted 16 April 2003 Abstract The aim of this review is to consider optical characteristics of terrestrial clouds. Both single and multiple light-scattering properties of water clouds are studied. The numerous results discussed can be used for solutions to both inverse and direct problems of cloud optics. An introduction to main microphysical characteristics of water and ice clouds, including the effective size, the liquid water content and path, the concentration of particles, is given. The refractive index of water and ice, which is of importance for optical waves propagation in clouds, is also considered. We consider extinction and absorption coefficients, phase functions, and asymmetry parameters of water and ice clouds and their relationships with the size, shape, and concentration of water droplets and ice crystals. Simple analytical results for absorption, reflection, and transmission characteristics of cloudy media are given. They are valid for optically thick clouds with optical thickness larger than 5. We have reviewed studies of polarization of solar light reflected from clouds. Image transfer problems have been considered as well. Modern methods of passive remote sensing of water and ice clouds are discussed. The review is finished by the discussion of optical properties of inhomogeneous clouds, which is a main topic of modern cloud optics research. D 2003 Elsevier B.V. All rights reserved. Keywords: Radiative transfer; Light scattering and propagation; Water and ice clouds 1. Introduction serve as a blanket to protect the Earth’s surface against cooling at night. This is due to the fact that the Water, ice, and mixed clouds are major regulators of maximum of the terrestrial emission is in the far infra- solar fluxes in the terrestrial atmosphere (Kondratyev red, where water droplets are highly absorbing. and Binenko, 1984; Liou, 1992, 2002). They reflect a Clouds, mists, and fogs are very common. They large portion of incoming visible radiation back to reduce the visibility of objects in the atmosphere and outer space. The light energy absorbed by water drop- limit capabilities of atmospheric vision, remote sens- lets and ice crystals leads to heating of atmospheric ing, and detection systems (Zege et al., 1991). Thus, it layers. Another important role of cloudy media is to is of a great importance to understand the peculiarities of light interaction with cloudy media, which can be considered as a huge ‘‘colloid’’, composed of liquid * Institute of Environmental Physics, University of Bremen, and solid water particles, dispersed in the air. It should P.O. Box 330440. Otto Hahn Allee 1, D-28334 Bremen, Germany. Tel.: +49-421-218-4475; fax: +49-421-218-4555. be pointed out that water droplets and air around them E-mail address: [email protected] can be contaminated by various fine particles (e.g., (A. Kokhanovsky). soot and dust particles). These aerosol particles influ- 0012-8252/$ - see front matter D 2003 Elsevier B.V. All rights reserved. doi:10.1016/S0012-8252(03)00042-4 190 A. Kokhanovsky / Earth-Science Reviews 64 (2004) 189–241 ence both light-scattering and absorption properties of 2. Microphysical characteristics cloudy media, making the studies of light propagation in cloudy media even more difficult (Menon et al., 2.1. Water clouds 2002). The very existence of clouds is due to fine- aerosol particles, the so-called cloud nuclei (Twomey, 2.1.1. Particle-size distributions 1977), with typical radii between 5 and 200 nm Water clouds consist of small liquid droplets that (Mason, 1975). generally have the spherical shape although particles Studies of optical and microphysical properties of of other shapes can exist due to different external cloudy media have a long and fruitful history. The influences. For instance, the deformation of large results of these investigations have been summarized in particles due to the gravitation force is of importance numerous books and papers (Kondratyev and Binenko, for raining clouds with particles having radii 1 mm 1984; Zege et al., 1991; Liou, 1992, 2002; Kokhanov- and larger (Macke and Grossklaus, 1998). The aver- sky, 2001a). The main properties of cloudy media are age radius of droplets in nonraining water clouds is well understood now, but unsolved problems remain. usually around 10 Am and the approximation of The most important of these include the accounting for spherical particles works quite well. Natural clouds the three-dimensional shape of clouds (Evans, 1998; with droplets of uniform size throughout never occur Mackeetal.,1999;Schreier,2001;Schreierand due to the variability of physical properties of air both Macke, 2001), and their inhomogenity in horizontal in space and time domains (Twomey, 1977). Thus, and vertical directions (Cahalan et al., 1994, 2001; one can consider a radius of a droplet, a, as a random Platnick, 2000, 2001). The influence of aerosols inside value, which is characterized by the distribution cloudy media, which can be one of explanations of the function f(a). This function is normalized by the anomalous absorption paradox (Danielson et al., 1969; following condition: Rozenberg et al., 1978; Stephens and Tsay, 1990), also Z l should be clarified. f ðaÞda ¼ 1: ð2:1Þ Another current issue is the characterization of 0 optical properties of ice clouds, which have extremely complex microstructure (Liou, 1992, 2002; Liou and The integral Takano, 1994; Macke et al., 1996; Yang and Liou, Z 1998; Kokhanovsky and Macke, 1999; Yang et al., a2 FðaÞ¼ f ðaÞda ð2:2Þ 2000, 2001) and appear almost with the same fre- a1 quency as water clouds. One rarely finds two identical crystals in ice clouds because preferential shapes vary gives the fraction of particles with radii between a1 with temperature and pressure (Mason, 1975), which and a2 in a unit volume of a cloud. The distribution vary across cloudy media (Yang et al., 2001).It function f(a) can be represented as a histogram, should be stressed that optical properties of a single graphically or in a tabular form (Ayvazian, 1991). particle and, as a result, optical properties of a cloud However, it is the most common to use an analytical as a whole are highly influenced by particles’ shapes form of this function, involving only two or three (Mishchenko et al., 1995, 1996, 1999, 2000). parameters (Deirmendjian, 1969). Of course, this is a A complete review across all fields of cloud optics, great simplification of real situations occurring in which is in a state of a rapid transition, would be natural clouds, but most optical characteristics of a difficult within a single book, not to mention in a single cloud as a whole practically do not depend on the fine article. Thus, I will concentrate mostly on analytical structures of particle-size distributions (PSD) f(a) results, which can be used for cloud optical properties (Hansen and Travis, 1974). McGraw et al. (1998) studies. The formulae presented can be applied for found that the local optical properties of polydisper- rapid estimations of light fluxes in cloudy atmosphere sions can be modelled with high accuracy by just the and will assist understanding the information content of first six moments of the particle-size distribution, and transmitted and reflection functions of cloudy media in the use of certain combinations of moments can respect to microphysical characteristics of clouds. reduce the number of parameters even further. A. Kokhanovsky / Earth-Science Reviews 64 (2004) 189–241 191 In most cases, the function f(a) can be represented Cðl þ 4Þ hWi¼ w0; ð2:13Þ by the gamma distribution (Deirmendjian, 1969): l3Cðl þ 1Þ l Àl a f ðaÞ¼Na e a0 ; ð2:3Þ where where 3 4pa0 2 v0 ¼ ; s0 ¼ 4pa ; w0 ¼ qv0 ð2:14Þ llþ1 3 0 N ¼ lþ1 ð2:4Þ Cðl þ 1Þa0 are corresponding parameters for monodispersed par- ticles with radii a . One can obtain in the case of the is the normalization constant and C(l +1) is the 0 most often employed cloud model with a0 =4Am and Gamma function. It follows that the first derivative l = 6 (Cloud C.1 model of Deirmendjian, 1969): f V(a0) = 0 and the second derivative f U(a0) < 0 (see Eq. (2.3)). Thus, the function (Eq. (2.3)) has the maximum 7 14 7 hVi¼ v0; hRi¼ s0; hWi¼ w0; ð2:15Þ at a = a0. Note that Eq. (2.4) follows from Eq. (2.1) 3 9 3 and the definition of the Gamma function: c À 16 3 c À 12 2 Z l where v0 2.7 Â 10 m , s0 2 Â 10 m , c À 10 CðlÞ¼ xlÀ1eÀxdx: ð2:5Þ w0 2.7 Â 10 g. Although parameters (Eq. 0 (2.14)) are small, the very large numbers of cloud One can see that the parameter l characterizes the droplets (typically, 100 particles in cm3)create width of the particle-size distribution f(a), being important factors for atmospheric processes (see next smaller for wider distributions. Moments section). Z l Eq. (2.3) allows to characterize the cloud droplet n n ha i¼ a f ðaÞda ð2:6Þ distribution only by two parameters: a0 and l. 0 However, it should be remembered that neither is of the distribution (Eq. (2.3)) are calculated from the constant and can vary inside the body of a cloud. following simple analytical equation Thus, their values depend on the averaging scale, with large averaging scales producing more broad a n Cðl þ n þ 1Þ hani¼ 0 : ð2:7Þ particle-size distributions with smaller values of l.
Load more

Recommended publications
  • Plant Lighting Basics and Applications
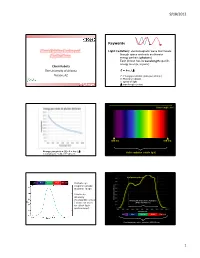
    9/18/2012 Keywords Plant Lighting Basics and Light (radiation): electromagnetic wave that travels through space and exits as discrete Applications energy packets (photons) Each photon has its wavelength-specific energy level (E, in joule) Chieri Kubota The University of Arizona E = h·c / Tucson, AZ E: Energy per photon (joule per photon) h: Planck’s constant c: speed of light Greensys 2011, Greece : wavelength (meter) Wavelength （nm） 380 nm 780 nm Energy per photon [J]: E = h·c / Visible radiation (visible light) mole photons = 6.02 x 1023 photons Leaf photosynthesis UV Blue Green Red Far red Human eye response peaks at green range. Luminous intensity (footcandle or lux Photosynthetically Active Radiation ) does not work (PAR, 400-700 nm) for plant light environment. UV Blue Green Red Far red Plant biologically active radiation (300-800 nm) 1 9/18/2012 Chlorophyll a Phytochrome response Chlorophyll b UV Blue Green Red Far red Absorption spectra of isolated chlorophyll Absorptance 400 500 600 700 Wavelength (nm) Daily light integral (DLI or Daily Light Unit and Terminology PPF) Radiation Photons Visible light •Total amount of photosynthetically active “Base” unit Energy (J) Photons (mol) Luminous intensity (cd) radiation (400‐700 nm) received per sq Flux [total amount received Radiant flux Photon flux Luminous flux meter per day or emitted per time] (J s-1) or (W) (mol s-1) (lm) •Unit: mole per sq meter per day (mol m‐2 d‐1) Flux density [total amount Radiant flux density Photon flux (density) Illuminance, • Under optimal conditions, plant growth is received per area per time] (W m-2) (mol m-2 s-1) Luminous flux density highly correlated with DLI.
    [Show full text]
  • Applied Spectroscopy Spectroscopic Nomenclature
    Applied Spectroscopy Spectroscopic Nomenclature Absorbance, A Negative logarithm to the base 10 of the transmittance: A = –log10(T). (Not used: absorbancy, extinction, or optical density). (See Note 3). Absorptance, α Ratio of the radiant power absorbed by the sample to the incident radiant power; approximately equal to (1 – T). (See Notes 2 and 3). Absorption The absorption of electromagnetic radiation when light is transmitted through a medium; hence ‘‘absorption spectrum’’ or ‘‘absorption band’’. (Not used: ‘‘absorbance mode’’ or ‘‘absorbance band’’ or ‘‘absorbance spectrum’’ unless the ordinate axis of the spectrum is Absorbance.) (See Note 3). Absorption index, k See imaginary refractive index. Absorptivity, α Internal absorbance divided by the product of sample path length, ℓ , and mass concentration, ρ , of the absorbing material. A / α = i ρℓ SI unit: m2 kg–1. Common unit: cm2 g–1; L g–1 cm–1. (Not used: absorbancy index, extinction coefficient, or specific extinction.) Attenuated total reflection, ATR A sampling technique in which the evanescent wave of a beam that has been internally reflected from the internal surface of a material of high refractive index at an angle greater than the critical angle is absorbed by a sample that is held very close to the surface. (See Note 3.) Attenuation The loss of electromagnetic radiation caused by both absorption and scattering. Beer–Lambert law Absorptivity of a substance is constant with respect to changes in path length and concentration of the absorber. Often called Beer’s law when only changes in concentration are of interest. Brewster’s angle, θB The angle of incidence at which the reflection of p-polarized radiation is zero.
    [Show full text]
  • CNT-Based Solar Thermal Coatings: Absorptance Vs. Emittance
    coatings Article CNT-Based Solar Thermal Coatings: Absorptance vs. Emittance Yelena Vinetsky, Jyothi Jambu, Daniel Mandler * and Shlomo Magdassi * Institute of Chemistry, The Hebrew University of Jerusalem, Jerusalem 9190401, Israel; [email protected] (Y.V.); [email protected] (J.J.) * Correspondence: [email protected] (D.M.); [email protected] (S.M.) Received: 15 October 2020; Accepted: 13 November 2020; Published: 17 November 2020 Abstract: A novel approach for fabricating selective absorbing coatings based on carbon nanotubes (CNTs) for mid-temperature solar–thermal application is presented. The developed formulations are dispersions of CNTs in water or solvents. Being coated on stainless steel (SS) by spraying, these formulations provide good characteristics of solar absorptance. The effect of CNT concentration and the type of the binder and its ratios to the CNT were investigated. Coatings based on water dispersions give higher adsorption, but solvent-based coatings enable achieving lower emittance. Interestingly, the binder was found to be responsible for the high emittance, yet, it is essential for obtaining good adhesion to the SS substrate. The best performance of the coatings requires adjusting the concentration of the CNTs and their ratio to the binder to obtain the highest absorptance with excellent adhesion; high absorptance is obtained at high CNT concentration, while good adhesion requires a minimum ratio between the binder/CNT; however, increasing the binder concentration increases the emissivity. The best coatings have an absorptance of ca. 90% with an emittance of ca. 0.3 and excellent adhesion to stainless steel. Keywords: carbon nanotubes (CNTs); binder; dispersion; solar thermal coating; absorptance; emittance; adhesion; selectivity 1.
    [Show full text]
  • Direct Insolation Models
    SERI/TR-33S-344 UC CATEGORY: UC-S9,61,62,63 DIRECT INSOLATION MODELS RICHARD BIRD ROLAND L. HULSTROM JANUARY 1980 PREPARED UNDER TASK No. 3623.01 Solar Energy Research Institute 1536 Cole Boulevard Golden. Colorado 80401 A Division of Midwest Research Institute Prepared for the U.S_ Department of Energy Contract No_ EG-77-C-01-4042 , '. Printed in the United States of America Available from: National Technical Information Service U.S. Departm ent of Commerce 5285 Port Royal Road Springfi e1dt VA 22161 Price: Microfiche $3.00 Printed Copy $ 5.25 NOTICE This report was prepared as an account of work sponsored by the United States Govern­ ment. Neither the United States nor the United States Department of Energy, nor any of their employees, nor any of their contractors, subcontractors, or their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness or usefulness of any information, apparatus, product or process dis closed, or represents that its us e would not infringe privately owned rights. S=�I TR-344 FOREWORD This re port documents wo rk pe rforme d by the SERI Energy Resource Assessment Branch for the Division of Solar Energy Technology of the U.S. De pa rtment of Energy. The re po rt compares several simple direct insolation models with a rigorous solar transmission model and describes an improved , simple, direct insolation model. Roland L. Hulstrom , Branch Chief Energy Resource Assessment , \ Approved for: SOLAR ENERGY RE SEARCH INSTITUTE for Research iii S=�I TR-344 TABLE OF CONTENTS 1.0 Introduction •••••••••••••••••••••••••••••••••••••••••••••••••••••••• 1 2.0 Description of Models •••••••••••• .
    [Show full text]
  • Lighting: the Principles
    TECHNICAL GUIDE Cross Sector AHDB Fellowship CP 085 Dr Phillip Davis, Stockbridge Technology Centre Lighting: The principles Filmed over 3 weeks at Stockbridge Technology Centre SCAN WITH LAYAR APP 2 TECHNICAL GUIDE Lighting: The principles CONTENTS SECTION ONE LIGHT AND LIGHTING SECTION THREE LEDS IN HORTICULTURE 1.1 What is light? 6 3.1 Crop growth under red and blue LEDs 21 1.2 The natural light environment and its 3.2 The influences of other colours of impact on plant light responses 6 light on crop growth 22 1.3 The measurement of light 6 3.3 End of day, day extension and night interruption lighting 23 1.3.1 Photometric light measurement – lumens and lux 6 3.4 Interlighting 23 1.3.2 Radiometric light measurement – Watts per 3.5 Propagation 24 metre squared or Joules per metre squared 8 3.6 Improving crop quality 24 1.3.3 Photon counts – Moles 8 3.6.1 Improving crop morphology and reducing 1.3.4 Daily light integrals (DLI) 10 the use of plant growth regulators 24 1.4 Conversions between different 3.6.2 Improving pigmentation 25 measurement units 10 3.6.3 Improving flavour and aroma 26 1.5 Assessing light quality 10 3.7 Lighting strategies 26 1.6 Overview of light technologies 10 3.8 Other lighting techniques 27 1.6.1 Incandescent and halogen bulbs 10 3.9 Insect management under LEDs 27 1.6.2 Fluorescent tubes 10 3.10 Plant pathogens and their interactions 1.6.3 High intensity discharge lamps 11 with light 28 1.6.4 Plasma and sulphur lamps 12 3.11 Conclusions 28 1.6.5 LED technology 12 SECTION FOUR OTHER INFORMATION SECTION TWO PLANT LIGHT RESPONSES 4.1 References 30 2.1 Photosynthesis 15 2.2 Light stress – Photoinhibition 15 2.3 Sensing light quality 18 2.4 UVB light responses 18 2.5 Blue and UVA light responses 18 2.6 Green light responses 18 2.7 Red and far-red light responses 19 2.8 Hormones and light 19 3 TECHNICAL GUIDE Lighting: The principles GLOSSARY Cryptochrome A photoreceptor that is sensitive to blue and UVA light.
    [Show full text]
  • Relation of Emittance to Other Optical Properties *
    JOURNAL OF RESEARCH of the National Bureau of Standards-C. Engineering and Instrumentation Vol. 67C, No. 3, July- September 1963 Relation of Emittance to Other Optical Properties * J. C. Richmond (March 4, 19G3) An equation was derived relating t he normal spcctral e mittance of a n optically in homo­ geneous, partially transmitting coating appli ed over an opaque substrate t o t he t hi ckncs and optical properties of t he coating a nd the reflectance of thc substrate at thc coaLin g­ SLI bstrate interface. I. Introduction The 45 0 to 0 0 luminous daylight r efl ectance of a composite specimen com prising a parLiall:\' transparent, spectrally nonselective, ligh t-scattering coating applied to a completely opaque (nontransmitting) substrate, can be computed from the refl ecta.nce of the substrate, the thi ck­ ness of the coaLin g and the refl ectivity and coefficien t of scatter of the coating material. The equaLions derived [01' these condi tions have been found by experience [1 , 2)1 to be of considerable praeLical usefulness, even though sever al factors ar e known to exist in real m aterials that wer e no t consid ered in the derivation . For instance, porcelain enamels an d glossy paints have significant specular refl ectance at lhe coating-air interface, and no r ea'! coating is truly spectrally nonselective. The optical properties of a material vary with wavelength , but in the derivation of Lh e equations refened to above, they ar e consid ered to be independent of wavelength over the rather narrow wavelength band encompassin g visible ligh t.
    [Show full text]
  • The Effects of Physical Parameters on the Absorption Coefficient of Natural Waters
    AN ABSTRACT OF THE THESIS OF W. Scott Pegau for the degree of Doctor of Philosophy in Oceanography presented on February 23, 1996. Title: The Effects of Physical Parameters on the Absorption Coefficient of Natural Waters. Abstract approved: Redacted for privacy J. Ronald V. Zaneveld The absorption coefficient is one of the fundamental parameters used for studies in hydrologic optics. The significance of this parameter makes it important to understand how to properly measure it and how the absorption of components, such as water, depend on physical parameters such as temperature and salinity. A discussion is provided of a majority of the techniques available for measuring the absorption coefficient. Results from a comparison of the techniques indicates that natural variability in the optical properties is an important factor to consider when comparing or reporting measured values of the absorption coefficient. The agreement between methods was found to be best at longer wavelengths where the absorption by water is a significant portion of the total absorption coefficient. In order to test the accuracy of measurements of the absorption coefficient a practical TOP closure equation is developed. Application of the equation to field measurements is limited by our ability to measure the volume scattering function. The dependence of the absorption coefficient of water on temperature and salinity is investigated. It was found that the absorption coefficient in the near infrared portion of the spectrum is strongly dependent on temperature and salinity. In the visible region the only portion with a temperature dependence > 0.00 1 m1/°C is in the neighborhood of 610 nm.
    [Show full text]
  • Radiometry and Photometry
    Radiometry and Photometry Wei-Chih Wang Department of Power Mechanical Engineering National TsingHua University W. Wang Materials Covered • Radiometry - Radiant Flux - Radiant Intensity - Irradiance - Radiance • Photometry - luminous Flux - luminous Intensity - Illuminance - luminance Conversion from radiometric and photometric W. Wang Radiometry Radiometry is the detection and measurement of light waves in the optical portion of the electromagnetic spectrum which is further divided into ultraviolet, visible, and infrared light. Example of a typical radiometer 3 W. Wang Photometry All light measurement is considered radiometry with photometry being a special subset of radiometry weighted for a typical human eye response. Example of a typical photometer 4 W. Wang Human Eyes Figure shows a schematic illustration of the human eye (Encyclopedia Britannica, 1994). The inside of the eyeball is clad by the retina, which is the light-sensitive part of the eye. The illustration also shows the fovea, a cone-rich central region of the retina which affords the high acuteness of central vision. Figure also shows the cell structure of the retina including the light-sensitive rod cells and cone cells. Also shown are the ganglion cells and nerve fibers that transmit the visual information to the brain. Rod cells are more abundant and more light sensitive than cone cells. Rods are 5 sensitive over the entire visible spectrum. W. Wang There are three types of cone cells, namely cone cells sensitive in the red, green, and blue spectral range. The approximate spectral sensitivity functions of the rods and three types or cones are shown in the figure above 6 W. Wang Eye sensitivity function The conversion between radiometric and photometric units is provided by the luminous efficiency function or eye sensitivity function, V(λ).
    [Show full text]
  • Principles of the Measurement of Solar Reflectance, Thermal Emittance, and Color
    Principles of the Measurement of Solar Reflectance, Thermal Emittance, and Color Contents Roof Heat Transfer Electromagnetic Radiation Radiative Properties of Surfaces Measuring Solar Radiation Measuring Solar Reflectance Measuring Thermal Emittance Measuring Color 1. Roof Heat Transfer 3 Roof surface is heated by solar absorption, cooled by thermal emission + convection Radiative Cooling Convective Solar Cooling Absorption Troof Insulatio n T Qin = U (Troof – inside Tinside) Most solar heat gain is dissipated by convective and radiative cooling… ...because the conduction heat transfer coefficient is much less than those for convection & radiation 2. Electromagnetic Radiation 7 The electromagnetic spectrum spans radio waves to gamma rays This includes sunlight (0.3 – 2.5 μm) and thermal IR radiation (4 – 80 μm) (0.4 – 0.7 All surfaces emit temperature-dependent electromagnetic radiation • Stefan-Boltzmann law • Blackbody cavity is a perfect absorber and emitter of radiation • Total blackbody radiation [W m-2] = σ T 4, where – σ = 5.67 10-8 W m-2 K-4 – T = absolute temperature [K] • At 300 K (near room temperature) σ T 4 = 460 W m-2 Higher surface temperatures → shorter wavelengths Solar radiation from sun's surface (5,800 K) peaks near 0.5 μm (green) Thermal radiation from ambient surfaces (300 K) peaks near 10 μm (infrared) Extraterrestrial sunlight is attenuated by absorption and scattering in atmosphere Global (hemispherical) solar radiation = direct (beam) sunlight + diffuse skylight Pyranometer measures global (a.k.a. Pyranometer hemi-spherical) sunlight on with horizontal surface sun-tracking shade Pyrheliometer measures measures direct (a.k.a. collimated, diffuse beam) light from sun skylight Let's compare rates of solar heating and radiative cooling Spectral heating rate of a black roof facing the sky on a 24-hour average basis, shown on a log scale.
    [Show full text]
  • Principles of Radiation Measurement
    Principles of Radiation Measurement This report presents a comprehensive summary of the terminology and units used in radiometry, photometry, and the measurement of photosynthetically active radiation (PAR). Measurement errors can arise from a number of sources, and these are explained in detail. Finally, the conversion of radiometric and photometric units to photon units is discussed. In this report, the International System of Units (SI) is used unless noted otherwise.9 Radiometry component of sunlight plus the diffuse component of skylight received together on a horizontal surface). This Radiometry1 is the measurement of the properties of physical quantity is measured by a pyranometer such as radiant energy (SI unit: joule, J), which is one of the many the LI-200R. Unit: W m-2. interchangeable forms of energy. The rate of flow of radi- ant energy, in the form of an electromagnetic wave, is Direct Solar Radiation is the radiation emitted from the called the radiant flux (unit: watt, W; 1 W = 1 J s-1). Radi- solid angle of the sun’s disc, received on a surface per- ant flux can be measured as it flows from the source (the pendicular to the axis of this cone, comprising mainly sun, in natural conditions), through one or more reflect- unscattered and unreflected solar radiation. This physical -2 ing, absorbing, scattering and transmitting media (the quantity is measured by a pyrheliometer. Unit: W m . Earth’s atmosphere, a plant canopy, etc.) to the receiving Diffuse Solar Radiation (sky radiation) is the downward surface of interest (e.g. a photosynthesizing leaf).8 scattered and reflected radiation coming from the whole hemisphere, with the exception of the solid angle sub- Terminology and Units tended by the sun’s disc.
    [Show full text]
  • Principles and Techniques of Remote Sensing
    EE/Ae 157a Introduction to the Physics and Techniques of Remote Sensing Week 2: Nature and Properties of Electromagnetic Waves 2-1 TOPICS TO BE COVERED • Fundamental Properties of Electromagnetic Waves – Electromagnetic Spectrum, Maxwell’s Equations, Wave Equation, Quantum Properties of EM Radiation, Polarization, Coherency, Group and Phase Velocity, Doppler Effect • Nomenclature and Definition of Radiation Quantities – Radiation Quantities, Spectral Quantities, Luminous Quantities • Generation of Electromagnetic Radiation • Detection of Electromagnetic Radiation • Overview of Interaction of EM Waves with Matter • Interaction Mechanisms Throughout the Electromagnetic Spectrum 2-2 ELECTROMAGNETIC SPECTRUM 2-3 MAXWELL’S EQUATIONS B E t D H J t B 0r H D 0 rE E 0 B 0 2-4 WAVE EQUATION From Maxwell’s Equations, we find: E H 0 r t 2E 0 r 0 r t 2 E E 2E 2E 2E 0 0 r 0 r t2 This is the free-space wave equation 2-5 SOLUTION TO THE WAVE EQUATION For a sinusoidal field, the wave equation reduces to 2 2 E 2 E 0 cr The solution to this equation is of the form E Aei kr t The speed of light is given by 1 c0 cr 0 r 0r r r 2-6 QUANTUM PROPERTIES OF EM RADIATION • Maxwell’s equations describe mathematically smooth motion of fields. • For very short wavelengths, it fails to describe certain significant phenomena when the wave interacts with matter. • In those cases, a quantum description is more appropriate. • In this description, the EM radiation is presented by a quantized burst with energy Q proportional to the
    [Show full text]
  • On Kirchhoff's Law and Its Generalized Application to Absorption and Emission by Cavities *
    JOURNAL OF RESEARCH of the National Bureau of Standards-B. Mathematics and Mathematical Physics Vol. 69B, No.3, July-September 1965 On Kirchhoff's Law and Its Generalized Application to Absorption and Emission by Cavities * Francis J. Kelly (March 15, 1965) Severa l a uthurs have ma de the assumption that Kirc hhoff's Law holds fur the apparent local s pec­ tral e mittance and apparent lo cal s pectral absorptance of a ny point on the inte rior s urface of a cavity. The correctness of this assumption is de monstrate d under cert ain general cunditiuns, and it s practi cal appli cati on to the calc ul ation of the tota l Aux a bsorbed by a cavit y or s pacecraft is di scussed. A fur­ ther app li cation to the case of a nunisothe rmal cavity ur spacecraft is de rived. By this de rivati on a n easy methud fur determining the total Au x e mitt ed fru lll s uc h a nonisothe rmal cavity is found when the di s tribution of the appare nt lucal s pectral e mittance uf the is uthermal c avity is known. T he economy and versatility of this methud is s hown by the calc ulation of the total Au x e mitt ed from a noni solhermal cylindrical cavit y for several a rbitra ry cases of te mpe rature di s tribution on the int e rior s urface of the c avity. Finally, the int egra l eq uation for a diffuse cav it y whose wall e mittance varies with position on the wall is tra nsformed to an e quation havi ng a symme tric kernel.
    [Show full text]