DOCSLIB.ORG

Intensity Wave Length

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Intensity Wave Length Module 9 Radiative Transfer in the Atmosphere 9.1 Introduction It has been emphasized in earlier lectures that energy from Sun drives the circulation of the atmosphere and ocean. Earth receives energy from Sun as ultraviolet, visible and near-infrared radiation. This radiation band is called the short wave radiation or radiation with wavelengths λ < 4 µm . An equal amount of energy is re-emitted by earth to maintain an overall energy balance. Earth emits energy in the form of infrared thermal radiation or longwave radiation with wavelengths λ > 4 µm . These two bands shown in Fig. 9.1 pertain to the wavelength intervals given as, Band 1: Solar spectrum 0.1− 4 µm (1 µm = 10−6 m) Band 2: Infrared region 4 −100 µm Sun Earth Fig. 9.1 Blackbody emission at the temperatures of Sun and Earth. 6000 K 288 K Intensity Overlap region Overlap 0.1 0.5 1 5 10 50 100 Wave length ( µ m ) Microwave radiation is not important for energy balance of the earth, but it finds wide use in remote sensing of the earth system because it is capable of penetrating through clouds. The study of radiative transfer in atmosphere and ocean is important because it leads to (i) a better understanding of energy transfer in these two components of the climate system; and (ii) in interpreting remote sensing measurements from satellites. Radiation is described by flux, intensity and radiance; and there are certain terms also that are frequently used while discussing the mathematics of the radiative transfer. First of all, it is required to calculate a differential amount of radiant energy dEλ ( J ) in a wavelength ( µm ) interval λ and λ + dλ that crosses an area ( m2 ) element dA in time (seconds) interval dt in a direction confined by an arc dω of the solid angle (steradian abbreviated as sr ). Some frequently used terms in radiative transfer are defined below and their dimensions (given in brackets) indicate how they are interrelated. Radiant Energy: The energy of radiation beam at a given wavelength (J) . Flux: Radiant energy crossing unit area per unit time ( Js−1m−2 or Wm−2 ). Intensity: Flux in unit wavelength and unit solid angle (W m−2µm−1 sr−1 ) Flux density or irradiance: Normal component of intensity integrated over the hemispheric solid angle (W m−2µm−1 ). It is the emittance of an emitting surface. Extinction: Loss of energy from a photon due to absorption and scattering. 1 Radiative decay: Electron falls back to the original state by re-emitting photon of same energy and same frequency. Photodissociation: Absorption of solar photons leading to breakdown of molecules initiating photochemical reactions and photo-ionization (i.e. outer electrons are stripped from atoms). Absorption: At sufficiently high pressures, molecular collisions are likely to occur and as a result of molecular collisions energy of excitation will be transferred to other forms of energy before re-emission could take place. In such situations, the photon is said to have been absorbed. Due to absorption of energy of excitation, the kinetic energy is produced, which is shared between molecules by collisional interaction. Since thermal energy is the macroscopic expression of molecular kinetic energy, the increased kinetic energy of molecules leads to local heating. In this process the photon energy has been transferred to heat. This process is also called “thermalization” or “quenching”. Scattering: Scattering of a photon of given energy and frequency by an atmospheric molecule implies that electron falls back to ground state re-emitting photon of same energy and frequency as the original one but in random direction. There are two kinds of scattering that occur in the atmosphere. Scattering by air molecules (Rayleigh) gives the blue colour to the sky; and scattering by aerosol particles (such as dust), called the Mie scattering, produces most scenic sunsets or sunrises. Thermal (infra-red) cooling: Thermal photons are also absorbed or scattered much like solar photons. When emitted, the energy is drawn from molecular kinetic energy leading to cooling of the atmosphere. Thus, radiant energy dEλ and the intensity Iλ are related as follows: dEλ = Iλ dAdλ dω dt (9.1) 9.2 Absorbing constituents in the atmosphere The main constituents that absorb radiation in different wavelength regions (or bands) are shown in Fig. 9.2. One may conspicuously note in this figure two atmospheric windows where the absorption is weak: one in the solar spectrum of the wavelengths 0.3 < λ < 1 µm (visible) and the other in the infrared region of wavelengths 8 < λ < 12 µm . Ozone (O3), water vapour (H2O) and carbon dioxide (CO2) are the dominant absorbers that primarily heat the atmosphere though oxygen (O2) also absorbs radiation in the ultraviolet and the visible region of the electromagnetic spectrum. In the solar spectrum ( λ < 4 µm ), O3 absorbs radiation in the ultraviolet and visible region; both CO2 and water vapour are greenhouse gases and absorb radiation in the near infrared region 1 < λ < 3.5 µm . In the infrared region, radiation is weakly absorbed by CO, CH4 and N2O in the troposphere, but CO2 and water vapour are the strong absorbers. In the atmospheric window region, 8 < λ < 12 µm , absorption is weak by these gases except for a band near λ = 9.6 µm which is associated with ozone (O3). The atmospheric window regions in the visible and infrared wavelength bands are important for remote sensing of atmosphere; that is why satellites are regularly launched by different countries in the space and their constellation forms an important part of the earth observing system. Electromagnetic radiation, a packet of different waves, is characterized by wavelength, frequency and wave number. Wavelength is denoted by λ; wave number is the reciprocal of wavelength; frequency is the product of wave number and the speed of 2 light with which all electromagnetic waves propagate. Wavelength (λ), wave number (ν~) and frequency (ν) are thus related as: 1 ν c ν = = and ν = cν~ = , c is the speed of light. λ c λ Fig. 9.2: The electromagnetic spectrum and the main atmospheric absorbents Small variations in the speed of light in air produce mirage and distortions, which indeed limit the resolution of ground based telescopes. Moreover, differences in the speed of light in air and water produce beautiful rainbows. Wavelength is expressed in the units of micrometre ( µm ). Based on wavelength (or frequency or wave number), energy can be partitioned according to wavelength bands. However, for radiative transfer in the atmosphere, radiation is categorized into two wave bands: Shortwave radiation: λ < 4 µm energy associated with solar (downwelling) radiation Longwave radiation: λ > 4 µm energy associated with terrestrial (upwelling) radiation Monochromatic radiation: refers to radiation of one single frequency or wavelength (i.e. single colour radiation). Similar meaning is also ascribed to monochromatic radiance. Visible Region: 0.39 ≤ λ ≤ 0.76 µm ; that is, the wavelengths sensed by the eye. Photon: Discrete packets of radiation; each photon contains energy E = hν . 9.3 Black-body radiation It is the radiation emitted from a small hole that has been cut in an isothermal cavity whose walls are maintained at a uniform temperature. The radiation is isotropic and the spectral energy density (the energy per unit volume per unit frequency interval) depends only on one frequency and cavity wall temperature. Thus, a blackbody surface completely absorbs all incident radiation to it. Most caves appear nearly black as all the sunlight rays that enter the cave are absorbed in multiple reflections and only a small fraction of sunlight (incident) emerges out from the entrance. The Planck function: According to the Planck’s Law (the first fundamental law of radiation), spectral energy density of the blackbody radiation at temperature T is given by 8π hν 3 u (T ) = (9.2) ν c3 {exp[hν / (kT )]−1} 3 −34 Here uν (T ) is the spectral energy density of blackbody radiation; h = 6.6262 ×10 J s 23 1 (Planck constant), k = 1.38062 ×10− J K − (Boltzmann constant) and c is the speed of 8 −1 light (c = 2.99792458 ×10 ms ). The energy density of a group of photons moving within a small arc of the solid angle Δω steradians is given by uν Δω / (4π ) ; 4π is the solid angle of the sphere. Then the energy flow at speed c by this group of photons is given as ⎛ uν Δω ⎞ c uν c ⎜ ⎟ = = Bν (T ) (9.3) ⎝ 4π ⎠ Δω 4π Using the expression of uν (T ) , we obtain an expression for the Planck function Bν (T ) as 2hν 3 B (T ) = (Planck Function) (9.4) ν c2 {exp[hν / (kT )]−1} Bν (T ) is the power per unit area, per unit solid angle, per unit frequency interval (spectral radiance) of blackbody radiation. The Planck function may also be expressed as a function of wavelength λ and temperature T, and it reads as: 2hc2 B (T ) = Wm−3 sr−1 or Wm−2sr−1µm−1 . (9.5) λ λ 5 exp[hc / (λkT )]−1 ( ) { } Since h, c and k are constant, the intensity of radiation Bλ(T) may be written as: −5 c1λ 2 −16 2 Bλ (T ) = ; c1 = 2πhc = 3.74 ×10 W m ; c2 π exp −1 c = hc / k= 1.45 ×10−2 mK. (9.6) { λT } 2 Thus Bλ (T ) is the blackbody spectral radiance written in terms of power (W ) per unit area (m−2 ) , per unit solid angle (sr−1) , per unit wavelength interval (m−1 or µm−1) . Whenever radiation and matter interact; photons are absorbed, scattered or emitted by molecules of the optically active gas If Bλ (T ) is integrated over all wavelengths, then one obtains the following expression for the blackbody radiance, ∞ σ 2k 4π 5 B (T )dλ = T 4 , σ = = 5.67 ×10−8 Wm−2K −4 (9.7) ∫ λ 3 2 0 π 15h c ∞ x3 π 4 In evaluating the above integral we use, dx = .
Load more

Recommended publications
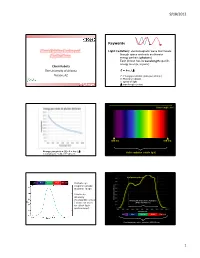
  • Plant Lighting Basics and Applications
    9/18/2012 Keywords Plant Lighting Basics and Light (radiation): electromagnetic wave that travels through space and exits as discrete Applications energy packets (photons) Each photon has its wavelength-specific energy level (E, in joule) Chieri Kubota The University of Arizona E = h·c / Tucson, AZ E: Energy per photon (joule per photon) h: Planck’s constant c: speed of light Greensys 2011, Greece : wavelength (meter) Wavelength （nm） 380 nm 780 nm Energy per photon [J]: E = h·c / Visible radiation (visible light) mole photons = 6.02 x 1023 photons Leaf photosynthesis UV Blue Green Red Far red Human eye response peaks at green range. Luminous intensity (footcandle or lux Photosynthetically Active Radiation ) does not work (PAR, 400-700 nm) for plant light environment. UV Blue Green Red Far red Plant biologically active radiation (300-800 nm) 1 9/18/2012 Chlorophyll a Phytochrome response Chlorophyll b UV Blue Green Red Far red Absorption spectra of isolated chlorophyll Absorptance 400 500 600 700 Wavelength (nm) Daily light integral (DLI or Daily Light Unit and Terminology PPF) Radiation Photons Visible light •Total amount of photosynthetically active “Base” unit Energy (J) Photons (mol) Luminous intensity (cd) radiation (400‐700 nm) received per sq Flux [total amount received Radiant flux Photon flux Luminous flux meter per day or emitted per time] (J s-1) or (W) (mol s-1) (lm) •Unit: mole per sq meter per day (mol m‐2 d‐1) Flux density [total amount Radiant flux density Photon flux (density) Illuminance, • Under optimal conditions, plant growth is received per area per time] (W m-2) (mol m-2 s-1) Luminous flux density highly correlated with DLI.
    [Show full text]
  • Measurement of the Earth Radiation Budget at the Top of the Atmosphere—A Review
    Review Measurement of the Earth Radiation Budget at the Top of the Atmosphere—A Review Steven Dewitte * and Nicolas Clerbaux Observations Division, Royal Meteorological Institute of Belgium, 1180 Brussels, Belgium; [email protected] * Correspondence: [email protected]; Tel.: +32-2-3730624 Received: 25 September 2017; Accepted: 1 November 2017; Published: 7 November 2017 Abstract: The Earth Radiation Budget at the top of the atmosphere quantifies how the Earth gains energy from the Sun and loses energy to space. It is of fundamental importance for climate and climate change. In this paper, the current state-of-the-art of the satellite measurements of the Earth Radiation Budget is reviewed. Combining all available measurements, the most likely value of the Total Solar Irradiance at a solar minimum is 1362 W/m2, the most likely Earth albedo is 29.8%, and the most likely annual mean Outgoing Longwave Radiation is 238 W/m2. We highlight the link between long-term changes of the Outgoing Longwave Radiation, the strengthening of El Nino in the period 1985–1997 and the strengthening of La Nina in the period 2000–2009. Keywords: Earth Radiation Budget; Total Solar irradiance; Satellite remote sensing 1. Introduction The Earth Radiation Budget (ERB) at the top of the atmosphere describes how the Earth gains energy from the sun, and loses energy to space through reflection of solar radiation and the emission of thermal radiation. The ERB is of fundamental importance for climate since: (1) The global climate, as quantified e.g., by the global average temperature, is determined by this energy exchange.
    [Show full text]
  • Chapter 2 Solar and Infrared Radiation Fluxes
    Chapter 2 Solar and Infrared Radiation Chapter overview: • Fluxes • Energy transfer • Seasonal and daily changes in radiation • Surface radiation budget Fluxes Flux (F): The transfer of a quantity per unit area per unit time (sometimes called flux density). A flux can be thought of as the inflow or outflow of a quantity through the side of a fixed volume. Fluxes can occur in all three directions - Fx, Fy, and Fz What is the convention for the sign of a flux? We can consider fluxes of mass or of heat. What are the units for a mass flux or a heat flux? The amount of a quantity transferred through a given area (A) in a given time (Δt) can be calculated as: Amount = F ⋅ A⋅ Δt For a heat flux, the amount of heat transferred is represented by ΔQH. Note: The textbook discusses kinematic fluxes, but we will not discuss fluxes in these terms in ATOC 3050. Unlike the textbook, we will use the symbol F to represent fluxes, not kinematic fluxes. What processes can cause a heat flux? Radiant flux: The radiant energy per unit area per unit time. Radiant energy: Energy transferred by electromagnetic waves (radiation). Radiation emitted by the sun is referred to as solar or shortwave radiation. Shortwave radiation – refers to the wavelength band (< 4 µm) that carries most of the energy associated with solar radiation Solar constant (or total solar irradiance) (S0): The solar radiative flux, perpendicular to the solar beam, that enters the top of the atmosphere -2 S0 = 1366 W m Radiation emitted by the earth is referred to as longwave, terrestrial, or infrared radiation.
    [Show full text]
  • Applied Spectroscopy Spectroscopic Nomenclature
    Applied Spectroscopy Spectroscopic Nomenclature Absorbance, A Negative logarithm to the base 10 of the transmittance: A = –log10(T). (Not used: absorbancy, extinction, or optical density). (See Note 3). Absorptance, α Ratio of the radiant power absorbed by the sample to the incident radiant power; approximately equal to (1 – T). (See Notes 2 and 3). Absorption The absorption of electromagnetic radiation when light is transmitted through a medium; hence ‘‘absorption spectrum’’ or ‘‘absorption band’’. (Not used: ‘‘absorbance mode’’ or ‘‘absorbance band’’ or ‘‘absorbance spectrum’’ unless the ordinate axis of the spectrum is Absorbance.) (See Note 3). Absorption index, k See imaginary refractive index. Absorptivity, α Internal absorbance divided by the product of sample path length, ℓ , and mass concentration, ρ , of the absorbing material. A / α = i ρℓ SI unit: m2 kg–1. Common unit: cm2 g–1; L g–1 cm–1. (Not used: absorbancy index, extinction coefficient, or specific extinction.) Attenuated total reflection, ATR A sampling technique in which the evanescent wave of a beam that has been internally reflected from the internal surface of a material of high refractive index at an angle greater than the critical angle is absorbed by a sample that is held very close to the surface. (See Note 3.) Attenuation The loss of electromagnetic radiation caused by both absorption and scattering. Beer–Lambert law Absorptivity of a substance is constant with respect to changes in path length and concentration of the absorber. Often called Beer’s law when only changes in concentration are of interest. Brewster’s angle, θB The angle of incidence at which the reflection of p-polarized radiation is zero.
    [Show full text]
  • Section 22-3: Energy, Momentum and Radiation Pressure
    Answer to Essential Question 22.2: (a) To find the wavelength, we can combine the equation with the fact that the speed of light in air is 3.00 " 108 m/s. Thus, a frequency of 1 " 1018 Hz corresponds to a wavelength of 3 " 10-10 m, while a frequency of 90.9 MHz corresponds to a wavelength of 3.30 m. (b) Using Equation 22.2, with c = 3.00 " 108 m/s, gives an amplitude of . 22-3 Energy, Momentum and Radiation Pressure All waves carry energy, and electromagnetic waves are no exception. We often characterize the energy carried by a wave in terms of its intensity, which is the power per unit area. At a particular point in space that the wave is moving past, the intensity varies as the electric and magnetic fields at the point oscillate. It is generally most useful to focus on the average intensity, which is given by: . (Eq. 22.3: The average intensity in an EM wave) Note that Equations 22.2 and 22.3 can be combined, so the average intensity can be calculated using only the amplitude of the electric field or only the amplitude of the magnetic field. Momentum and radiation pressure As we will discuss later in the book, there is no mass associated with light, or with any EM wave. Despite this, an electromagnetic wave carries momentum. The momentum of an EM wave is the energy carried by the wave divided by the speed of light. If an EM wave is absorbed by an object, or it reflects from an object, the wave will transfer momentum to the object.
    [Show full text]
  • CNT-Based Solar Thermal Coatings: Absorptance Vs. Emittance
    coatings Article CNT-Based Solar Thermal Coatings: Absorptance vs. Emittance Yelena Vinetsky, Jyothi Jambu, Daniel Mandler * and Shlomo Magdassi * Institute of Chemistry, The Hebrew University of Jerusalem, Jerusalem 9190401, Israel; [email protected] (Y.V.); [email protected] (J.J.) * Correspondence: [email protected] (D.M.); [email protected] (S.M.) Received: 15 October 2020; Accepted: 13 November 2020; Published: 17 November 2020 Abstract: A novel approach for fabricating selective absorbing coatings based on carbon nanotubes (CNTs) for mid-temperature solar–thermal application is presented. The developed formulations are dispersions of CNTs in water or solvents. Being coated on stainless steel (SS) by spraying, these formulations provide good characteristics of solar absorptance. The effect of CNT concentration and the type of the binder and its ratios to the CNT were investigated. Coatings based on water dispersions give higher adsorption, but solvent-based coatings enable achieving lower emittance. Interestingly, the binder was found to be responsible for the high emittance, yet, it is essential for obtaining good adhesion to the SS substrate. The best performance of the coatings requires adjusting the concentration of the CNTs and their ratio to the binder to obtain the highest absorptance with excellent adhesion; high absorptance is obtained at high CNT concentration, while good adhesion requires a minimum ratio between the binder/CNT; however, increasing the binder concentration increases the emissivity. The best coatings have an absorptance of ca. 90% with an emittance of ca. 0.3 and excellent adhesion to stainless steel. Keywords: carbon nanotubes (CNTs); binder; dispersion; solar thermal coating; absorptance; emittance; adhesion; selectivity 1.
    [Show full text]
  • UNIT 1 ELECTROMAGNETIC RADIATION Radiation
    Electromagnetic UNIT 1 ELECTROMAGNETIC RADIATION Radiation Structure 1.1 Introduction Objectives 1.2 What is Electromagnetic Radiation? Wave Mechanical Model of Electromagnetic Radiation Quantum Model of Electromagnetic Radiation 1.3 Consequences of Wave Nature of Electromagnetic Radiation Interference Diffraction Transmission Refraction Reflection Scattering Polarisation 1.4 Interaction of EM Radiation with Matter Absorption Emission Raman Scattering 1.5 Summary 1.6 Terminal Questions 1.7 Answers 1.1 INTRODUCTION You would surely have seen a beautiful rainbow showing seven different colours during the rainy season. You know that this colourful spectrum is due to the separation or dispersion of the white light into its constituent parts by the rain drops. The rainbow spectrum is just a minute part of a much larger continuum of the radiations that come from the sun. These are called electromagnetic radiations and the continuum of the electromagnetic radiations is called the electromagnetic spectrum. In the first unit of this course you would learn about the electromagnetic radiation in terms of its nature, characteristics and properties. Spectroscopy is the study of interaction of electromagnetic radiation with matter. We would discuss the ways in which different types of electromagnetic radiation interact with matter and also the types of spectra that result as a consequence of the interaction. In the next unit you would learn about ultraviolet-visible spectroscopy ‒ a consequence of interaction of electromagnetic radiation in the ultraviolet-visible
    [Show full text]
  • Realization of a Micrometre-Sized Stochastic Heat Engine Valentin Blickle1,2* and Clemens Bechinger1,2
    Erschienen in: Nature Physics ; 8 (2012), 2. - S. 143-146 https://dx.doi.org/10.1038/nphys2163 Realization of a micrometre-sized stochastic heat engine Valentin Blickle1,2* and Clemens Bechinger1,2 The conversion of energy into mechanical work is essential trapping centre and k(t), the time-dependent trap stiffness. The for almost any industrial process. The original description value of k is determined by the laser intensity, which is controlled of classical heat engines by Sadi Carnot in 1824 has largely by an acousto-optic modulator. By means of video microscopy, the shaped our understanding of work and heat exchange during two-dimensional trajectory was sampled with spatial and temporal macroscopic thermodynamic processes1. Equipped with our resolutions of 10 nm and 33 ms, respectively. Keeping hot and cold present-day ability to design and control mechanical devices at reservoirs thermally isolated at small length scales is experimentally micro- and nanometre length scales, we are now in a position very difficult to achieve, so rather than coupling our colloidal to explore the limitations of classical thermodynamics, arising particle periodically to different heat baths, here we suddenly on scales for which thermal fluctuations are important2–5. Here changed the temperature of the surrounding liquid. we demonstrate the experimental realization of a microscopic This variation of the bath temperature was achieved by a second heat engine, comprising a single colloidal particle subject to a coaxially aligned laser beam whose wavelength was matched to an time-dependent optical laser trap. The work associated with absorption peak of water. This allowed us to heat the suspension the system is a fluctuating quantity, and depends strongly from room temperature to 90 ◦C in less than 10 ms (ref.
    [Show full text]
  • Radiation Exchange Between Surfaces
    Chapter 1 Radiation Exchange Between Surfaces 1.1 Motivation and Objectives Thermal radiation, as you know, constitutes one of the three basic modes (or mechanisms) of heat transfer, i.e., conduction, convection, and radiation. Actually, on a physical basis, there are only two mechanisms of heat transfer; diffusion (the transfer of heat via molecular interactions) and radiation (the transfer of heat via photons/electomagnetic waves). Convection, being the bulk transport of a fluid, is not precisely a heat transfer mechanism. The physics of radiation transport are distinctly different than diffusion transport. The latter is a local phenomena, meaning that the rate of diffusion heat transfer, at a point in space, precisely depends only on the local nature about the point, i.e., the temperature gradient and thermal conductivity at the point. Of course, the temperature field will depend on the boundary and initial conditions imposed on the system. However, the diffusion heat flux at, say, one point in the system does not directly effect the diffusion flux at some distant point. Radiation, on the other hand, is not local; the flux of radiation at a point will, in general, be directly and instantaneously dependent on the radiation flux at all points in a system. Unlike diffusion, radiation can act over a distance. Accordingly, the mathematical description of radiation transport will employ an integral equation for the radiation field, as opposed to the differential equation for heat diffusion. Our objectives in studying radiation in the short amount of time left in the course will be to 1. Develop a basic physical understanding of electromagnetic radiation, with emphasis on the properties of radiation that are relevant to heat transfer.
    [Show full text]
  • Properties of Electromagnetic Waves Any Electromagnetic Wave Must Satisfy Four Basic Conditions: 1
    Chapter 34 Electromagnetic Waves The Goal of the Entire Course Maxwell’s Equations: Maxwell’s Equations James Clerk Maxwell •1831 – 1879 •Scottish theoretical physicist •Developed the electromagnetic theory of light •His successful interpretation of the electromagnetic field resulted in the field equations that bear his name. •Also developed and explained – Kinetic theory of gases – Nature of Saturn’s rings – Color vision Start at 12:50 https://www.learner.org/vod/vod_window.html?pid=604 Correcting Ampere’s Law Two surfaces S1 and S2 near the plate of a capacitor are bounded by the same path P. Ampere’s Law states that But it is zero on S2 since there is no conduction current through it. This is a contradiction. Maxwell fixed it by introducing the displacement current: Fig. 34-1, p. 984 Maxwell hypothesized that a changing electric field creates an induced magnetic field. Induced Fields . An increasing solenoid current causes an increasing magnetic field, which induces a circular electric field. An increasing capacitor charge causes an increasing electric field, which induces a circular magnetic field. Slide 34-50 Displacement Current d d(EA)d(q / ε) 1 dq E 0 dt dt dt ε0 dt dq d ε E dt0 dt The displacement current is equal to the conduction current!!! Bsd μ I μ ε I o o o d Maxwell’s Equations The First Unified Field Theory In his unified theory of electromagnetism, Maxwell showed that electromagnetic waves are a natural consequence of the fundamental laws expressed in these four equations: q EABAdd 0 εo dd Edd s BE B s μ I μ ε dto o o dt QuickCheck 34.4 The electric field is increasing.
    [Show full text]
  • Hybrid Electrochemical Capacitors
    Florida International University FIU Digital Commons FIU Electronic Theses and Dissertations University Graduate School 1-11-2018 Hybrid Electrochemical Capacitors: Materials, Optimization, and Miniaturization Richa Agrawal Department of Mechanical and Materials Engineering, Florida International University, [email protected] DOI: 10.25148/etd.FIDC006581 Follow this and additional works at: https://digitalcommons.fiu.edu/etd Part of the Materials Chemistry Commons, Materials Science and Engineering Commons, Nanoscience and Nanotechnology Commons, and the Physical Chemistry Commons Recommended Citation Agrawal, Richa, "Hybrid Electrochemical Capacitors: Materials, Optimization, and Miniaturization" (2018). FIU Electronic Theses and Dissertations. 3680. https://digitalcommons.fiu.edu/etd/3680 This work is brought to you for free and open access by the University Graduate School at FIU Digital Commons. It has been accepted for inclusion in FIU Electronic Theses and Dissertations by an authorized administrator of FIU Digital Commons. For more information, please contact [email protected]. FLORIDA INTERNATIONAL UNIVERSITY Miami, Florida HYBRID ELECTROCHEMICAL CAPACITORS: MATERIALS, OPTIMIZATION, AND MINIATURIZATION A dissertation submitted in partial fulfillment of the requirement for the degree of DOCTOR OF PHILOSOPHY in MATERIALS SCIENCE AND ENGINEERING by Richa Agrawal 2018 To: Dean John L. Volakis College of Engineering and Computing This dissertation entitled Hybrid Electrochemical Capacitors: Materials, Optimization, and Miniaturization, written
    [Show full text]
  • Direct Insolation Models
    SERI/TR-33S-344 UC CATEGORY: UC-S9,61,62,63 DIRECT INSOLATION MODELS RICHARD BIRD ROLAND L. HULSTROM JANUARY 1980 PREPARED UNDER TASK No. 3623.01 Solar Energy Research Institute 1536 Cole Boulevard Golden. Colorado 80401 A Division of Midwest Research Institute Prepared for the U.S_ Department of Energy Contract No_ EG-77-C-01-4042 , '. Printed in the United States of America Available from: National Technical Information Service U.S. Departm ent of Commerce 5285 Port Royal Road Springfi e1dt VA 22161 Price: Microfiche $3.00 Printed Copy $ 5.25 NOTICE This report was prepared as an account of work sponsored by the United States Govern­ ment. Neither the United States nor the United States Department of Energy, nor any of their employees, nor any of their contractors, subcontractors, or their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness or usefulness of any information, apparatus, product or process dis closed, or represents that its us e would not infringe privately owned rights. S=�I TR-344 FOREWORD This re port documents wo rk pe rforme d by the SERI Energy Resource Assessment Branch for the Division of Solar Energy Technology of the U.S. De pa rtment of Energy. The re po rt compares several simple direct insolation models with a rigorous solar transmission model and describes an improved , simple, direct insolation model. Roland L. Hulstrom , Branch Chief Energy Resource Assessment , \ Approved for: SOLAR ENERGY RE SEARCH INSTITUTE for Research iii S=�I TR-344 TABLE OF CONTENTS 1.0 Introduction •••••••••••••••••••••••••••••••••••••••••••••••••••••••• 1 2.0 Description of Models •••••••••••• .
    [Show full text]