Poteg-10-Guitar-Amps-B
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
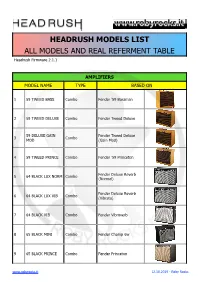
HEADRUSH MODELS LIST ALL MODELS and REAL REFERMENT TABLE Headrush Firmware 2.1.1
HEADRUSH MODELS LIST ALL MODELS AND REAL REFERMENT TABLE Headrush Firmware 2.1.1 AMPLIFIERS MODEL NAME TYPE BASED ON 1 59 TWEED BASS Combo Fender ’59 Bassman 2 59 TWEED DELUXE Combo Fender Tweed Deluxe 59 DELUXE GAIN Fender Tweed Deluxe 3 Combo MOD (Gain Mod) 4 59 TWEED PRINCE Combo Fender ’59 Princeton Fender Deluxe Reverb 5 64 BLACK LUX NORM Combo (Normal) Fender Deluxe Reverb 6 64 BLACK LUX VIB Combo (Vibrato) 7 64 BLACK VIB Combo Fender Vibroverb 8 65 BLACK MINI Combo Fender Champ 6w 9 65 BLACK PRINCE Combo Fender Princeton www.robyrocks.it 12.10.2019 - Roby Rocks 65 BLACK PRINCE 10 Combo Fender Princeton Reverb REV Fender Super Reverb 11 65 BLACK SR Combo “Blackface” Fender Twin Reverb 12 67 BLACK DUO Combo “Blackface” 13 67 BLACK SHIMMER Stack Fender Dual Showman 14 66 AC HI BOOST Combo Vox AC30 Top Boost 66 AC HI BOOST Vox AC30 Top Boost 15 Combo MOD (Mod) 16 66 FLIP BASS Stack Ampeg Portaflex B15-N 17 BLUE LINE BASS Stack Ampeg SVT 300w 69 BLUE LINE Ampeg SVT 300w 18 Stack SCOOP (Scooped) 19 65 J45 Stack Marshall JTM45 Marshall Super Lead Plexi 20 67 PLEXIGAS VARI Stack (Variac Mod) Marshall Super Lead Plexi 21 68 PLEXI EL84 MOD Stack (EL34 tubes mod) www.robyrocks.it 12.10.2019 - Roby Rocks Marshall Super Lead Plexi 22 68 PLEXIGLAS 100W Stack 100W Marshall Super Lead Plexi 23 68 PLEXIGLAS 50W Stack 50W Marshall JCM800 24 82 LEAD 800 100W Stack (Normal) 25 82 LEAD 800 50W Stack Marshall JCM800 50w 82 LEAD 800 BASS Marshall JCM800 (Bass 26 Stack MOD Mod) 82 LEAD 800 27 Stack Marshall JCM800 (Bright) BRIGHT 82 LEAD 800 TS Marshall -

Philips DEALING with TECHNICAL PROBLEMS
VOL. 5 N~. 3 . Philips DEALING WITH TECHNICAL PROBLEMS. RELATING TO THE PRODUCTS, PROCESSES AND. INVESTIGATIONS OF N.V. PHILIPS' GLOEILAMPENFABRIEKEN EDITED BY THE RESEARCH LABORATORY OF N.V. PHILIPS' GLOEILAMPENFABRIEKEN, EINDHOVEN, HOLLAND TESTING A~PLIFIER OUTPUT VALVES BY MEANS OF THE 'CAT~ODE RAY TUBE hy A. J. HEINS van der VEN. 621.317.755: 621.396.645 I n testing amplifier output valves, the most important data are contained in the In' v.. diagram if one knows over which part of the diagram the values of voltage and current prevailing during operatien range, i;e. if the position of the load line is known. The la- Vn 'diagrams as well as the load lines can very easily b~ obtained with the help of a 'cathode ray tube. The necessary apparatus is described in this article. A number of auxiliary ar- rangernents are also studied, by which the axes and the necessary calibration lines in the diagram can be traced on the fluorescent screen, and which make it possible to. cause the diagrams of two .output valves which are to be compared to appear simultancously on the screen. In order to obtain the load line in the correct place in the diagram, use must he made of dir'ect current push-pull amplifiers for the deflection voltages of the cathode ray tube. The position of the load line upon inductive loading is discussed and explained by a number of examples. In conclusion one,npplication of the instaflation in the develop- ment of output pentodes is dealt with. If one wishes to characterize briefly the perfor- quantrties are to some degree dependent _on the mance of an output valve of !tn amplifier or radio loading impedance which is included in the anode set, it is enough to give the sensitivity, the distor- circuit, it is first necessary to find out how the loa'd- tion as a function of the power output, and in some ing of the ~alve is e~pl'esse~ in the Ia- V~ curve.' , cases the maximum power which can he delivered mA without grid current flowing. -

Pentodes Connected As Triodes
Pentodes connected as Triodes by Tom Schlangen Pentodes connected as Triodes About the author Tom Schlangen Born 1962 in Cologne / Germany Studied mechanical engineering at RWTH Aachen / Germany Employments as „safety engineering“ specialist and CIO / IT-head in middle-sized companies, now owning and running an IT- consultant business aimed at middle-sized companies Hobby: Electron valve technology in audio Private homepage: www.tubes.mynetcologne.de Private email address: [email protected] Tom Schlangen – ETF 06 2 Pentodes connected as Triodes Reasons for connecting and using pentodes as triodes Why using pentodes as triodes at all? many pentodes, especially small signal radio/TV ones, are still available from huge stock cheap as dirt, because nobody cares about them (especially “TV”-valves), some of them, connected as triodes, can rival even the best real triodes for linearity, some of them, connected as triodes, show interesting characteristics regarding µ, gm and anode resistance, that have no expression among readily available “real” triodes, because it is fun to try and find out. Tom Schlangen – ETF 06 3 Pentodes connected as Triodes How to make a triode out of a tetrode or pentode again? Or, what to do with the “superfluous” grids? All additional grids serve a certain purpose and function – they were added to a basic triode system to improve the system behaviour in certain ways, for example efficiency. We must “disable” the functions of those additional grids in a defined and controlled manner to regain triode characteristics. Just letting them “dangle in vacuum unconnected” will not work – they would charge up uncontrolled in the electron stream, leading to unpredictable behaviour. -

Eimac Care and Feeding of Tubes Part 3
SECTION 3 ELECTRICAL DESIGN CONSIDERATIONS 3.1 CLASS OF OPERATION Most power grid tubes used in AF or RF amplifiers can be operated over a wide range of grid bias voltage (or in the case of grounded grid configuration, cathode bias voltage) as determined by specific performance requirements such as gain, linearity and efficiency. Changes in the bias voltage will vary the conduction angle (that being the portion of the 360° cycle of varying anode voltage during which anode current flows.) A useful system has been developed that identifies several common conditions of bias voltage (and resulting anode current conduction angle). The classifications thus assigned allow one to easily differentiate between the various operating conditions. Class A is generally considered to define a conduction angle of 360°, class B is a conduction angle of 180°, with class C less than 180° conduction angle. Class AB defines operation in the range between 180° and 360° of conduction. This class is further defined by using subscripts 1 and 2. Class AB1 has no grid current flow and class AB2 has some grid current flow during the anode conduction angle. Example Class AB2 operation - denotes an anode current conduction angle of 180° to 360° degrees and that grid current is flowing. The class of operation has nothing to do with whether a tube is grid- driven or cathode-driven. The magnitude of the grid bias voltage establishes the class of operation; the amount of drive voltage applied to the tube determines the actual conduction angle. The anode current conduction angle will determine to a great extent the overall anode efficiency. -

ELECTRIC GUITARS: Fender Custom Shop
Studio Contact 4 Union Street (+1) 207.756.9599 Camden, ME 04843 [email protected] GUITARS / BASSES / AMPS / STOMP-BOXES (SEE WEBSITE “GUITARSENAL” LINK FOR COMPLETE PHOTO GALLERY) ELECTRIC GUITARS: GUITAR AMPS / CABINETS: Fender Custom Shop ‘63 Tele Goldtop K&M 50 Watt Analog Design Custom (Dumble Circuit) Fender Custom Shop ‘52 Tele K&M 2x12 Cabinet (EVM 12L Black Label Speakers) Fender Custom Shop Tele Fender Super Reverb (Vintage Blackface circa ‘66) Fender Custom Shop ‘60s Strat Fender Super Reverb (Vintage Blackface circa ‘65) Fender Custom Shop ‘60s Relic Strat Fender Princeton Reverb (Vintage Silverface) Fender Strat Plus (Lace Pickups) Fender Deluxe Reverb (Jenson Special Design Speaker) Fender MIJ Squier Strat Fender Twin Reverb ’65 Reissue Fender Squire Strat Fender Blues Junior (EVM 12L Speaker) Gibson ES335 (Trapeze / Original PU / Circa 1966 Fender Princeton Chorus Gibson Les Paul Junior (Original P90s / Circa 1957) Fender Deluxe 90 DSP Gibson Reverse Firebird 3 (Circa 1964) Marshall 100 Watt Head (circa 1965) Gibson ES 120T (Jazzbox / Single Coil PU / Circa 1962) Marshall 1960a Cab (Cherry / Original Speakers / circa Gibson ES-335 Memphis Dot Reissue Custom Shop 1965) Gibson Les Paul Classic 1960 Reissue Marshall 1960b Cab (Original Speakers / circa 1965) Gibson Les Paul Studio Marshall 8x10 Cab (Original Speakers / circa 1966) CP Thornton Blues Queen Vox AC30 w/ Top Boost (Original Speakers / circa 1964) CP Thornton Elite E1 Soldano Speedster Head and Matching 1x12" Cab ESP Series 400 Strat-styled (Rosewood Fretboard) -

Mustang GTX 100 Manual
MUSTANG GTX50 MUSTANG GTX100 EXPANDED OWNER’S MANUAL REV. B CONTENTS Introduction 1 Control Panel 2 Rear Panel 3 Presets Preset Basics 4 Editing and Saving Presets 5 Editing Preset Amplifier Control Knob Settings 6 Replacing Preset Amplifier Models 8 List of Amplifier Models 9 List of Cabinet Models 10 Editing Effects 12 Editing Effects Settings 20 List of Effects Types 24 Menu Functions 28 Setlists 29 WiFi Use 32 Bluetooth Use 35 Built-in Tuner 37 Auxiliary and Headphone Jacks 38 USB Connectivity 38 Line Out and FX Send/Return 38 Footswitch Use GTX-7 Footswitch 39 Looper 42 EXP-1 Expression Pedal 45 EQ & Amp Settings 49 Global EQ 49 Line Out/USB Gain 50 Preset Organizer 51 Restore Settings and Restore All 53 About this Amp 54 Cloud Presets 54 Backup/Restore for Presets and Setlists 56 Firmware Updates and Factory Restore 60 Fender Tone™ App 62 Specifications 63 INTRODUCTION This expanded owner’s manual is a thorough user’s guide to the features and functions of the Mustang GTX50 and GTX100 amplifiers. As a complement to the Mustang GTX Quick Start Guide that comes with each amplifier, this manual pres- ents a deeper, more detailed look at Mustang GTX’s many versatile capabilities. This includes navigation and modification of the many onboard presets, and comprehensive descriptions of the many amplifier and effect models. It also includes step-by-step and fully illustrated instructions for using Mustang GTX’s Setlist, WiFi, Bluetooth, USB, onboard tuner, GTX-7 footswitch, EXP-1 Expression Pedal and looping functions. Mustang GTX’s tonal possibilities are virtually endless, especially when paired with the Fender Tone™ app (page 62). -

Sound Productions Backline Rentals Production Smaller Dec
BACKLINE RENTALS DRUM KITS PERCUSSION KEYBOARDS GUITARS GUITAR AMPS BASS GUITARS BASS AMPS GUITAR PEDALS & ACCS. DJ EQUIP. WIRELESS EQUIP. MIXING CONSOLES MISC EQUIP. For quotes & inquiries contact Greg Narkewicz at 972.550.0594 or [email protected] DRUM KITS DW Collectors Series Broken Glass Gretsch Renown Maple Pure Maple Kit Silver Sparkle Kicks : 20’’,22’’,24’’ Kick : 22’’ Rack Toms : 8’’.10’’,12’’,13’’,14’’ Rack Toms : 10’’,12’’ Floor Toms : 14’’,16’’,18’’ Floor Toms : 14’’,16’’ Snare : 14’’X6.5’’ Maple Snare : 14x5 Maple DW Collectors Series Curly Maple Ludwig Classic Maple Natural Finish Red Sparkle Kicks: 20’’,22’’,24’’ Kick : 22’’, 24’’ Rack Toms :8’’,10’’,12’’,13’’ Rack Toms : 10’’ , 12’’, 13’’ Floor Toms : 14’’,16’’,18’’ Floor Tom :2x 16’’ Snare: 14x5 Maple Snare : 6.5x14 Atlas-Pro Hardware Pearl Masterworks Red Sparkle Tama Starclassic Kick : 22’’ Cherry Sunburst Rack Toms : 10’’,12’’,13’’ Kick : 22’’ Floor Toms : 14’’,16’’ Rack Toms : 10’’ , 12’’ Snare : 14x6.5 Maple Signature Floor Tom : 16’’ Snare : 14x5’’ Gretsch Renown Maple Dark Brown Kick : 22’’ Yamaha Custom Recording Birch Rack Toms : 10’’,12’’ Black Hanging Floor Toms : 14’’,16’’ Kick : 22’’ Snare : 14x5 Maple Rack Toms : 10’’,12’’,13’’, 14’’ Floor Tom : 16’’ Snare : 14x7 Birch MoreDRUM KITS Yamaha Generic Kit Red Cymbal Brands Kick : 22’’ Zildjian Rack Toms : 12’’,13’’ Sabian Floor Tom : 16’’ Paiste Snare : 14x6.5 Chrome Yamaha Maple Custom Natural Finish Kick : 22’’ Rack Toms : 10’’,12’’,13’’ Hanging Floor Toms : 14’’,16’’ Snare : 14x4 Maple Yamaha Maple Custom Absolute Electric Blue Kicks : 20’’,22’’ Rack Toms : 8’’,10’’,12’’,13’’ Floor Toms : 14’’,16’’,18’’ Snare : 14x5 Maple Additional Snares Yamaha 13x6 Oak Yamaha 13x6 Brass Ludwig 14x6.5 Black Beauty Ludwig 14x5 Black Beauty Pearl 14x3 Brass Free Floater Mapex 13x5 Maple Pearl 10x5 Firecracker PERCUSSION Percussion L.P. -
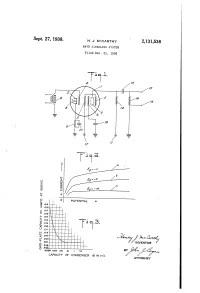
Sept. 27, 1938. H. J. Mcarthy 2,131,538 INVENTOR
Sept. 27, 1938. H. J. McArthy 2,131,538 WAWE SIGNALING SYSTEM Filed Dec. 31, 1936 INVENTOR CAPACITY OF CONDENSER 8 N m fid. AORNEY Patented Sept. 27, 1938 2,131,538 UNITED STATES PATENT OFFICE. 2,131,538 WAVE SIGNALENG SYSTEM Henry J. McCarthy, Danvers, Mass., assignor to Hygrade Sylvania Corporation, Salem, Mass., a corporation of Massachusetts Application December 31, 1936, Seria No. 8,532 4 Claims. (C. 179-11) : . This invention relates to Wave. Signaling Sys velope either of the metal or glass type. Suitably tems and more especially to such systems as supported within the envelope is a pentode employ electron discharge tubes of the suppreSSor mount comprising an electron emitting cathode grid type. 2. With its insulated heater filament 3; a control 5 The invention is in the nature of an improve grid 4; a shield grid 5; a suppressor grid 6; and ment. On the type of System disclosed in appli an anode or plate. It will be understood that cation Serial No. 13,047, filed March 26th, 1935. any Well-known structure and arrangement of There is disclosed in said application a System the electrodes may be employed, for example the employing a pentode tube of the Suppressor grid mount may be similar to that embodied in the O type Wherein the suppressing action is achieved tubes designated commercially by the type num 10: Without employing a conductive or metallic con bers 39/44, 41, 57, 78 and the like and while the nection between the Suppressor grid and the invention is primarily applicable to radio fre cathode. -

Guitar and Amp Tone
Jim Gleason’s GUITAR ENCYCLOPEDIA Guitar And Amp Tone By Jim Gleason Version 1. 0 © 1994-2006 Rock Performance Music. All Rights Reserved www.guitarencyclopedia.com PAGE 2 ALIGNING REFERENCES IN THIS MANUAL TO THE VIDEO CASSETTE On your video recorder (or with the remote), set the counter to zero (0:00:00) exactly at the beginning of the video, exactly where the title screen shown below first appears. It must be a REAL TIME COUNTER. GUITAR and AMP TONE By Jim Gleason ©1994 RPM All Rights Reserved You can then cue sections of the video by refering to the column on the far right of the Contents pages. CONTENTS PAGE 3 All entries in italics below are guitar and amp tone setups. Page Videotape Preview Of Sounds................................................................................................ on videotape only 0:00:04 Alligning Real Time Contents References To The Video Cassette Tape ................................ 2 Contents ................................................................................................................................ 3 Introduction A. The Proceedure Suggested By This Video and Book................................................... 5 B. Volume Control ............................................................................................................ 5 C. Distortion ...................................................................................................................... 6 D. Tone Control ................................................................................................................ -

AWE APR 1929 .Pdf
AMATEUR WIRELESS, APRIL 6, 1923 "BRITAIN'S FAVOURITE THREE -1929 MODEL Every Azsr i I Thursday() Vol. XIV.No. 356 Saturday, April 6, 1929 RITA1N'S AVOURITE Registered at the G.P.O. as a Nel...3-ttr t*, 3929 matter Whet, APRIL 6, l' 11 1S ? 9041014ofnatne is there adifference isonly Actuallyis aperfected there Ventone. Niullard that and. theVentonewhole thinli.valve tor the use ini0,titeatade world, with, its Sounap iathe it. in. byNkullard, increaseof betWeedifiereaeeonly behind llardin anan state alltheinade one tl-t artareptaation resultsafurther areeceiveradding, -valve. tradition. practiceogar by different, and stateobtainedsopa-powertobe valve "(beery that just all aown theoutputtoealaloviag VentooeAfterofits equal itthe veil volume call anative the araplification&alit perfortoancedeserve for its LS -We superiordoes but With ot its itself nosnob,inhand iaeldeatalki by is hand aclass Pentane beatbecauseis in toWorlz t Mulfordit pefers N.B.results brothers. best P, MullaYd IsarALOE 0.SAS The Mallard Wireless Service Co, Ltd., MullardHouse, Denmark Street, London, W.C.Z. Advertisers Appreciate Mention of "A.W." with Your Order APRIL 6, 1929 513 amour Wtraluj. THE AINvict 1 it I EXPEpts, LEWCOS COI LS ENGINEERING PRECISION... Engineering Precision has once again resulted in J.B. Condensers being chosen for yet another Star Circuit-in fact, it's no easy matter to -day to find a really high-class set which does not include these precision instruments. This time J.B. Logarithmic Condensers (Plain Type), are used in " Britain's Favourite Three " De Luxe, as described in this issue of " Amateur Wireless." These Condensers are the last word in ULTRA -SHORT- high-classdesign,possessinggreat SIX -PIN COILS WAVE COIL mechanical strength combined with the highest possible electrical efficiency. -

An Experimental Investigation of a Low Distortion Mixer
AN EXPERIMENTAL INVESTIGATION OF A LOW DISTORTION MIXER USING A BEAM-DEFLECTION TUBE A THESIS Presented to the Faculty of the Graduate Division By Guy Herbert Smith, Jr. In Partial. Fulfillment of the Requirements for the Degree Master of Science in Electrical Engineering Georgia Institute of Technology June, I96I "In presenting the dissertation as a partial fulfillment of the requirements for an advanced degree from the Georgia Institute of Technology, I agree that the Library of the Insti tution shall make it available for inspection and circulation in accordance with its regulations governing materials of this type. I agree that permission to copy from, or to publish from, this dissertation may be granted by the professor under whose di rection it was written, or,, in his .absence, by the dean, of the Graduate Division when such copying or publication is solely for scholarly purposes and does not involve potential financial gain. It is understood that any copying from, or publication of, this dissertation which involves potential financial gain will not be allowed without written permission. " /y~ J* AN EXPERIMENTAL INVESTIGATION OF A LOW DISTORTION MIXER USING A BEAM-DEFLECTION TUBE Approved: - \ A . \ h T T - / /) l Date Approved by Chairman: 11 PREFACE This study is an experimental investigation of a low distortion mixer using a beam-deflection tube as the active circuit element. The material herein is limited in its scope in that the investigation covers only one of several basic circuit configurations that are suitable for use with beam-deflection tubes. It is also limited because only one type of beam-deflection tube has been considered. -

SHARP-CUTOFF PENTODES.—(Continued)
570 RECEIVING TUBES [Sue. 14-4 14»4. Tetrodes and Pentodes.—Tetrodes and pentodes are most con• veniently classified according to function rather than to structure, and the tubes of this section will be classified primarily as r-f amplifiers or as power output tubes. There are many tubes which might be considered as belonging in either or both of these categories, but the great majority fall clearly into one or the other class. R-f Amplifiers.—R-f and i-f amplification in radio receivers is now almost invariably obtained from small pentodes, which may be classified on the basis of their cutoff characteristics into sharp-cutoff and remote- cutoff types. The latter type is occasionally and rather meaningless designated the "super control" type, and in some tube fists the former type is vaguely called a "triple grid amplifier." Some tubes are inter• mediate in character between the two classes, and are called "semi• remote-cutoff" pentodes; they may most conveniently be classed with the remote-cutoff tubes. Sharp-cutoff pentodes have Eg-Ip characteristics such that plate current and transconductance decrease to practically zero when the con• trol grid is made a few volts negative. In a remote-cutoff pentode they will decrease rapidly at first with increasing negative grid bias, but the rate of decrease becomes less and the quantities become essentially zero only when the negative bias becomes comparatively large. This remote- cutoff or variable-Mu characteristic is desirable when a variable bias ve£k- age is used to control the gain of the tube as in the ordinary receiver AVC circuit.