A Universal Scaling Law Between Gray Matter and White Matter of Cerebral Cortex
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Cerebral Cortex Structure, Function, Dysfunction Reading Ch 10 Waxman Dental Neuroanatomy Lecture Suzanne Stensaas, Ph.D
Cerebral Cortex Structure, Function, Dysfunction Reading Ch 10 Waxman Dental Neuroanatomy Lecture Suzanne Stensaas, Ph.D. March 15, 2011 Anatomy Review • Lobes and layers • Brodmann’s areas • Vascular Supply • Major Neurological Findings – Frontal, Parietal, Temporal, Occipital, Limbic • Quiz Questions? Types of Cortex • Sensory • Motor • Unimodal association • Multimodal association necessary for language, reason, plan, imagine, create Structure of neocortex (6 layers) The general pattern of primary, association and mulimodal association cortex (Mesulam) Brodmann, Lateral Left Hemisphere MCA left hemisphere from D.Haines ACA and PCA -Haines Issues of Functional Localization • Earliest studies -Signs, symptoms and note location • Electrical discharge (epilepsy) suggested function • Ablation - deficit suggest function • Reappearance of infant functions suggest loss of inhibition (disinhibition), i.e. grasp, suck, Babinski • Variabilities in case reports • Linked networks of afferent and efferent neurons in several regions working to accomplish a task • Functional imaging does not always equate with abnormal function associated with location of lesion • fMRI activation of several cortical regions • Same sign from lesions in different areas – i.e.paraphasias • Notion of the right hemisphere as "emotional" in contrast to the left one as "logical" has no basis in fact. Limbic System (not a true lobe) involves with cingulate gyrus and the • Hippocampus- short term memory • Amygdala- fear, agression, mating • Fornix pathway to hypothalamus • -

Structure and Function of Visual Area MT
AR245-NE28-07 ARI 16 March 2005 1:3 V I E E W R S First published online as a Review in Advance on March 17, 2005 I E N C N A D V A Structure and Function of Visual Area MT Richard T. Born1 and David C. Bradley2 1Department of Neurobiology, Harvard Medical School, Boston, Massachusetts 02115-5701; email: [email protected] 2Department of Psychology, University of Chicago, Chicago, Illinois 60637; email: [email protected] Annu. Rev. Neurosci. Key Words 2005. 28:157–89 extrastriate, motion perception, center-surround antagonism, doi: 10.1146/ magnocellular, structure-from-motion, aperture problem by HARVARD COLLEGE on 04/14/05. For personal use only. annurev.neuro.26.041002.131052 Copyright c 2005 by Abstract Annual Reviews. All rights reserved The small visual area known as MT or V5 has played a major role in 0147-006X/05/0721- our understanding of the primate cerebral cortex. This area has been 0157$20.00 historically important in the concept of cortical processing streams and the idea that different visual areas constitute highly specialized Annu. Rev. Neurosci. 0.0:${article.fPage}-${article.lPage}. Downloaded from arjournals.annualreviews.org representations of visual information. MT has also proven to be a fer- tile culture dish—full of direction- and disparity-selective neurons— exploited by many labs to study the neural circuits underlying com- putations of motion and depth and to examine the relationship be- tween neural activity and perception. Here we attempt a synthetic overview of the rich literature on MT with the goal of answering the question, What does MT do? www.annualreviews.org · Structure and Function of Area MT 157 AR245-NE28-07 ARI 16 March 2005 1:3 pathway. -
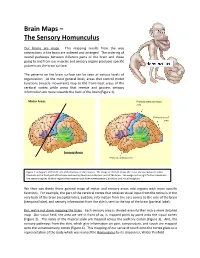
Brain Maps – the Sensory Homunculus
Brain Maps – The Sensory Homunculus Our brains are maps. This mapping results from the way connections in the brain are ordered and arranged. The ordering of neural pathways between different parts of the brain and those going to and from our muscles and sensory organs produces specific patterns on the brain surface. The patterns on the brain surface can be seen at various levels of organization. At the most general level, areas that control motor functions (muscle movement) map to the front-most areas of the cerebral cortex while areas that receive and process sensory information are more towards the back of the brain (Figure 1). Motor Areas Primary somatosensory area Primary visual area Sensory Areas Primary auditory area Figure 1. A diagram of the left side of the human cerebral cortex. The image on the left shows the major division between motor functions in the front part of the brain and sensory functions in the rear part of the brain. The image on the right further subdivides the sensory regions to show regions that receive input from somatosensory, auditory, and visual receptors. We then can divide these general maps of motor and sensory areas into regions with more specific functions. For example, the part of the cerebral cortex that receives visual input from the retina is in the very back of the brain (occipital lobe), auditory information from the ears comes to the side of the brain (temporal lobe), and sensory information from the skin is sent to the top of the brain (parietal lobe). But, we’re not done mapping the brain. -

The Human Brain Hemisphere Controls the Left Side of the Body and the Left What Makes the Human Brain Unique Is Its Size
About the brain Cerebrum (also known as the The brain is made up of around 100 billion nerve cells - each one cerebral cortex or forebrain) is connected to another 10,000. This means that, in total, we The cerebrum is the largest part of the brain. It is split in to two have around 1,000 trillion connections in our brains. (This would ‘halves’ of roughly equal size called hemispheres. The two be written as 1,000,000,000,000,000). These are ultimately hemispheres, the left and right, are joined together by a bundle responsible for who we are. Our brains control the decisions we of nerve fibres called the corpus callosum. The right make, the way we learn, move, and how we feel. The human brain hemisphere controls the left side of the body and the left What makes the human brain unique is its size. Our brains have a hemisphere controls the right side of the body. The cerebrum is larger cerebral cortex, or cerebrum, relative to the rest of the The human brain is the centre of our nervous further divided in to four lobes: frontal, parietal, occipital, and brain than any other animal. (See the Cerebrum section of this temporal, which have different functions. system. It is the most complex organ in our fact sheet for further information.) This enables us to have abilities The frontal lobe body and is responsible for everything we do - such as complex language, problem-solving and self-control. The frontal lobe is located at the front of the brain. -

Function of Cerebral Cortex
FUNCTION OF CEREBRAL CORTEX Course: Neuropsychology CC-6 (M.A PSYCHOLOGY SEM II); Unit I By Dr. Priyanka Kumari Assistant Professor Institute of Psychological Research and Service Patna University Contact No.7654991023; E-mail- [email protected] The cerebral cortex—the thin outer covering of the brain-is the part of the brain responsible for our ability to reason, plan, remember, and imagine. Cerebral Cortex accounts for our impressive capacity to process and transform information. The cerebral cortex is only about one-eighth of an inch thick, but it contains billions of neurons, each connected to thousands of others. The predominance of cell bodies gives the cortex a brownish gray colour. Because of its appearance, the cortex is often referred to as gray matter. Beneath the cortex are myelin-sheathed axons connecting the neurons of the cortex with those of other parts of the brain. The large concentrations of myelin make this tissue look whitish and opaque, and hence it is often referred to as white matter. The cortex is divided into two nearly symmetrical halves, the cerebral hemispheres . Thus, many of the structures of the cerebral cortex appear in both the left and right cerebral hemispheres. The two hemispheres appear to be somewhat specialized in the functions they perform. The cerebral hemispheres are folded into many ridges and grooves, which greatly increase their surface area. Each hemisphere is usually described, on the basis of the largest of these grooves or fissures, as being divided into four distinct regions or lobes. The four lobes are: • Frontal, • Parietal, • Occipital, and • Temporal. -

Neocortex: Consciousness Cerebellum
Grey matter (chips) White matter (the wiring: the brain mainly talks to itself) Neocortex: consciousness Cerebellum: unconscious control of posture & movement brains 1. Golgi-stained section of cerebral cortex 2. One of Ramon y Cajal’s faithful drawings showing nerve cell diversity in the brain cajal Neuropil: perhaps 1 km2 of plasma membrane - a molecular reaction substrate for 1024 voltage- and ligand-gated ion channels. light to Glia: 3 further cell types 1. Astrocytes: trophic interface with blood, maintain blood brain barrier, buffer excitotoxic neurotransmitters, support synapses astros Oligodendrocytes: myelin insulation oligos Production persists into adulthood: radiation myelopathy 3. Microglia: resident macrophages of the CNS. Similarities and differences with Langerhans cells, the professional antigen-presenting cells of the skin. 3% of all cells, normally renewed very slowly by division and immigration. Normal Neurosyphilis microglia Most adult neurons are already produced by birth Peak synaptic density by 3 months EMBRYONIC POSTNATAL week: 0 6 12 18 24 30 36 Month: 0 6 12 18 24 30 36 Year: 4 8 12 16 20 24 Cell birth Migration 2* Neurite outgrowth Synaptogenesis Myelination 1* Synapse elimination Modified from various sources inc: Andersen SL Neurosci & Biobehav Rev 2003 Rakic P Nat Rev Neurosci 2002 Bourgeois Acta Pediatr Suppl 422 1997 timeline 1 Synaptogenesis 100% * Rat RTH D BI E A Density of synapses in T PUBERTY primary visual cortex H at different times post- 0% conception. 100% (logarithmic scale) RTH Cat BI D E A T PUBERTY H The density values equivalent 0% to 100% vary between species 100% but in Man the peak value is Macaque 6 3 RTH 350 x10 synapses per mm BI D E PUBERTY A T The peak rate of synapse H formation is at birth in the 0% macaque: extrapolating to 100% the entire cortex, this Man RTH BI amounts to around 800,000 D E synapses formed per sec. -

Short- and Long-Term Deficits After Unilateral Ablation Andthe Effects of Subsequent Callosal Section’
0270.6474/84/0404-0918$02.00/0 The Journal of Neuroscience Copyright 0 Society for Neuroscience Vol. 4, No. 4, pp. 918-929 Printed in U.S.A. April 1984 SUPPLEMENTARY MOTOR AREA OF THE MONKEY’S CEREBRAL CORTEX: SHORT- AND LONG-TERM DEFICITS AFTER UNILATERAL ABLATION ANDTHE EFFECTS OF SUBSEQUENT CALLOSAL SECTION’ COBIE BRINKMAN Experimental Neurology Unit, The John Curtin School of Medical Research, Australian National University, Canberra, Australia 2601 Received March 7, 1983; Revised November 11, 1983; Accepted November 15, 1983 Abstract The short-term and long-term behavioral effects of unilateral lesions of the supplementary motor area (SMA) were studied in five monkeys (Mczcaca fascicularis ssp). A monkey with a unilateral lesion of the premotor area (PM) served as a control. In all animals, general behavior was unaffected by the lesions. For a few weeks postoperatively, all monkeys showed a clumsiness of forelimb movements, bilaterally, which involved both the distal and proximal muscles. Two SMA-lesioned monkeys (but not the PM-lesioned one), studied for up to 1 year postoperatively, showed a characteristic deficit of bimanual coordination where the two hands tended to behave in a similar manner instead of sharing the task between them. This deficit was more pronounced after a lesion contralateral to the nonpreferred hand. The deficit was interpreted as indicating that the intact SMA now influenced the motor outflow of both the ipsilateral hemisphere and the contralateral one through the corpus callosum. Callosal section immediately abolished the bimanual deficit, although the clumsiness returned transiently. The results imply that SMA may give rise normally to discharges informing the contralateral hemisphere of intended and/or ongoing movements via the corpus callosum. -

Neurogenesis in Adult Mammals: Some Progress and Problems
The Journal of Neuroscience, February 1, 2002, 22(3):619–623 Neurogenesis in Adult Mammals: Some Progress and Problems Elizabeth Gould and Charles G. Gross Department of Psychology, Princeton University, Princeton, New Jersey 08544 Approximately 40 years after its first report, the addition of addition, the growing evidence that glia communicate among neurons to the brains of adult mammals has now been generally themselves electrically and have many functional properties that accepted. We now know that several endocrine and experiential interact and overlap with neurons (Rose and Konnerth, 2001; variables modulate adult neurogenesis. However, several meth- Bezzi and Volterra, 2001) suggests that new glia may play a odological problems in its quantitative study remain. One is the significant role. use of low doses of the exogenous marker of cell proliferation, In the 1990s there were several developments that finally es- bromodeoxyuridine (BrdU). A second is the transient lifetime of tablished neurogenesis in the adult rodent. The first was the most of the adult-generated cells. A third is that the survival of introduction of cell type-specific markers for immunohistochem- new neurons may depend on stimuli that are lacking in standard ical identification of the phenotype of newly generated cells laboratory conditions. This review considers these issues as well (Cameron et al., 1993; Okano et al., 1993; Seki and Arai, 1993). as the possible functions of new neurons. These could be combined with 3H-thymidine labeling to deter- From the beginnings of modern neuroscience in the late 19th mine the identity of the new cells. The second was the introduc- century, it was assumed that the mammalian CNS became struc- tion of the thymidine analog BrdU as another in vivo marker of turally stable soon after birth and remained that way throughout proliferating cells (Miller and Nowakowski, 1988; Seki and Arai life. -

How Cells Fold the Cerebral Cortex
776 • The Journal of Neuroscience, January 24, 2018 • 38(4):776–783 Dual Perspectives Dual Perspectives Companion Paper: How Forces Fold the Cerebral Cortex, by Christopher D. Kroenke and Philip V. Bayly How Cells Fold the Cerebral Cortex Víctor Borrell Instituto de Neurociencias, Consejo Superior de Investigaciones Científicas & Universidad Miguel Herna´ndez, Sant Joan d’Alacant 03550, Spain Foldingofthecerebralcortexisashighlyintriguingaspoorlyunderstood.Atfirstsight,thismayappearassimpletissuecrumplinginside an excessively small cranium, but the process is clearly much more complex and developmentally predetermined. Whereas theoretical modeling supports a critical role for biomechanics, experimental evidence demonstrates the fundamental role of specific progenitor cell types, cellular processes, and genetic programs on cortical folding. Key words: basal Radial Glia; ferret; neurogenesis; OSVZ; Pax6; primate Introduction impact in defining the prospective patterns of cortical folding. In One of the most characteristic features of the human brain is its order for me to review the cellular mechanisms responsible for external folded appearance, due to the 3D arrangement of the cortical folding, I will first begin by defining what is cortical fold- cerebral cortex mantle forming outward folds and inward fis- ing, and what is not. sures. Folding patterns vary significantly between species, while being stereotyped within species. Developmental mechanisms re- Cortical folding sponsible for cortical folding are an intriguing and elusive ques- -
Anatomy of Cerebral Hemispheres Doctors Notes Notes/Extra Explanation Please View Our Editing File Before Studying This Lecture to Check for Any Changes
Color Code Important Anatomy of Cerebral Hemispheres Doctors Notes Notes/Extra explanation Please view our Editing File before studying this lecture to check for any changes. Objectives At the end of the lecture, the students should be able to: List the parts of the cerebral hemisphere (cortex, medulla, basal nuclei, lateral ventricle). Describe the subdivision of a cerebral hemisphere into lobes. List the important sulci and gyri of each lobe. Describe different types of fibers in cerebral medulla (association, projection and commissural) and give example of each type. Cerebrum Extra Corpus callosum o Largest part of the forebrain. ( makes up 2 / 3 rd weight off all brain) (recall: the forebrain gives the cerebral hemispheres and the diencephalon) o Divided into two halves, the cerebral hemispheres (right and left), which are separated Left hemisphere Right hemisphere by a deep median longitudinal fissure which lodges the falx cerebri*. o In the depth of the fissure, the hemispheres are connected by a bundle of fibers called the corpus callosum. *It is a large, crescent- shaped fold of meningeal layer of dura Median longitudinal fissure mater that descends vertically in the longitudinal fissure between the cerebral Extra Extra hemispheres Cerebrum Buried within the white matter Cerebral Hemispheres lie a number of nuclear masses The structure of cerebral hemipheres includes: (caudate, putamen, globus pallidus) collectively known as the basal ganglia. WM Deeper to the cortex, axons running to and from the cells of the cortex form an extensive mass of white matter (WM). Contains synapses (50 trillion) WM Superficial layer of grey matter, the cerebral cortex. -

Brain Anatomy
BRAIN ANATOMY Adapted from Human Anatomy & Physiology by Marieb and Hoehn (9th ed.) The anatomy of the brain is often discussed in terms of either the embryonic scheme or the medical scheme. The embryonic scheme focuses on developmental pathways and names regions based on embryonic origins. The medical scheme focuses on the layout of the adult brain and names regions based on location and functionality. For this laboratory, we will consider the brain in terms of the medical scheme (Figure 1): Figure 1: General anatomy of the human brain Marieb & Hoehn (Human Anatomy and Physiology, 9th ed.) – Figure 12.2 CEREBRUM: Divided into two hemispheres, the cerebrum is the largest region of the human brain – the two hemispheres together account for ~ 85% of total brain mass. The cerebrum forms the superior part of the brain, covering and obscuring the diencephalon and brain stem similar to the way a mushroom cap covers the top of its stalk. Elevated ridges of tissue, called gyri (singular: gyrus), separated by shallow groves called sulci (singular: sulcus) mark nearly the entire surface of the cerebral hemispheres. Deeper groves, called fissures, separate large regions of the brain. Much of the cerebrum is involved in the processing of somatic sensory and motor information as well as all conscious thoughts and intellectual functions. The outer cortex of the cerebrum is composed of gray matter – billions of neuron cell bodies and unmyelinated axons arranged in six discrete layers. Although only 2 – 4 mm thick, this region accounts for ~ 40% of total brain mass. The inner region is composed of white matter – tracts of myelinated axons. -

A Scoping Review of Neuromodulation Techniques in Neurodegenerative Diseases: a Useful Tool for Clinical Practice?
medicina Review A Scoping Review of Neuromodulation Techniques in Neurodegenerative Diseases: A Useful Tool for Clinical Practice? Fabio Marson 1,2 , Stefano Lasaponara 3,4 and Marco Cavallo 5,6,* 1 Research Institute for Neuroscience, Education and Didactics, Fondazione Patrizio Paoletti, 06081 Assisi, Italy; [email protected] 2 Department of Human Neuroscience, Sapienza University of Rome, 00185 Rome, Italy 3 Department of Psychology, Sapienza University of Rome, 00185 Rome, Italy; [email protected] 4 Department of Human Sciences, LUMSA University, 00193 Rome, Italy 5 Faculty of Psychology, eCampus University, 22060 Novedrate, Italy 6 Clinical Psychology Service, Saint George Foundation, 12030 Cavallermaggiore, Italy * Correspondence: [email protected]; Tel.: +39-347-830-6430 Abstract: Background and Objectives: Neurodegenerative diseases that typically affect the elderly such as Alzheimer’s disease, Parkinson’s disease and frontotemporal dementia are typically char- acterised by significant cognitive impairment that worsens significantly over time. To date, viable pharmacological options for the cognitive symptoms in these clinical conditions are lacking. In recent years, various studies have employed neuromodulation techniques to try and contrast patients’ decay. Materials and Methods: We conducted an in-depth literature review of the state-of-the-art of the contribution of these techniques across these neurodegenerative diseases. Results: The present review reports that neuromodulation techniques targeting cognitive impairment do not allow to Citation: Marson, F.; Lasaponara, S.; Cavallo, M. A Scoping Review of draw yet any definitive conclusion about their clinical efficacy although preliminary evidence is very Neuromodulation Techniques in encouraging. Conclusions: Further and more robust studies should evaluate the potentialities and Neurodegenerative Diseases: A limitations of the application of these promising therapeutic tools to neurodegenerative diseases.