Cdma2000 1X Capacity Decrease by Power Control Error in High Speed Train Environment
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

NEXT GENERATION MOBILE WIRELESS NETWORKS: 5G CELLULAR INFRASTRUCTURE JULY-SEPT 2020 the Journal of Technology, Management, and Applied Engineering
VOLUME 36, NUMBER 3 July-September 2020 Article Page 2 References Page 17 Next Generation Mobile Wireless Networks: Authors Dr. Rendong Bai 5G Cellular Infrastructure Associate Professor Dept. of Applied Engineering & Technology Eastern Kentucky University Dr. Vigs Chandra Professor and Coordinator Cyber Systems Technology Programs Dept. of Applied Engineering & Technology Eastern Kentucky University Dr. Ray Richardson Professor Dept. of Applied Engineering & Technology Eastern Kentucky University Dr. Peter Ping Liu Professor and Interim Chair School of Technology Eastern Illinois University Keywords: The Journal of Technology, Management, and Applied Engineering© is an official Mobile Networks; 5G Wireless; Internet of Things; publication of the Association of Technology, Management, and Applied Millimeter Waves; Beamforming; Small Cells; Wi-Fi 6 Engineering, Copyright 2020 ATMAE 701 Exposition Place Suite 206 SUBMITTED FOR PEER – REFEREED Raleigh, NC 27615 www. atmae.org JULY-SEPT 2020 The Journal of Technology, Management, and Applied Engineering Next Generation Mobile Wireless Networks: Dr. Rendong Bai is an Associate 5G Cellular Infrastructure Professor in the Department of Applied Engineering and Technology at Eastern Kentucky University. From 2008 to 2018, ABSTRACT he served as an Assistant/ The requirement for wireless network speed and capacity is growing dramatically. A significant amount Associate Professor at Eastern of data will be mobile and transmitted among phones and Internet of things (IoT) devices. The current Illinois University. He received 4G wireless technology provides reasonably high data rates and video streaming capabilities. However, his B.S. degree in aircraft the incremental improvements on current 4G networks will not satisfy the ever-growing demands of manufacturing engineering users and applications. -

Cellular Wireless Networks
CHAPTER10 CELLULAR WIRELESS NETwORKS 10.1 Principles of Cellular Networks Cellular Network Organization Operation of Cellular Systems Mobile Radio Propagation Effects Fading in the Mobile Environment 10.2 Cellular Network Generations First Generation Second Generation Third Generation Fourth Generation 10.3 LTE-Advanced LTE-Advanced Architecture LTE-Advanced Transission Characteristics 10.4 Recommended Reading 10.5 Key Terms, Review Questions, and Problems 302 10.1 / PRINCIPLES OF CELLULAR NETWORKS 303 LEARNING OBJECTIVES After reading this chapter, you should be able to: ◆ Provide an overview of cellular network organization. ◆ Distinguish among four generations of mobile telephony. ◆ Understand the relative merits of time-division multiple access (TDMA) and code division multiple access (CDMA) approaches to mobile telephony. ◆ Present an overview of LTE-Advanced. Of all the tremendous advances in data communications and telecommunica- tions, perhaps the most revolutionary is the development of cellular networks. Cellular technology is the foundation of mobile wireless communications and supports users in locations that are not easily served by wired networks. Cellular technology is the underlying technology for mobile telephones, personal communications systems, wireless Internet and wireless Web appli- cations, and much more. We begin this chapter with a look at the basic principles used in all cellular networks. Then we look at specific cellular technologies and stan- dards, which are conveniently grouped into four generations. Finally, we examine LTE-Advanced, which is the standard for the fourth generation, in more detail. 10.1 PRINCIPLES OF CELLULAR NETWORKS Cellular radio is a technique that was developed to increase the capacity available for mobile radio telephone service. Prior to the introduction of cellular radio, mobile radio telephone service was only provided by a high-power transmitter/ receiver. -

Guidelines on Mobile Device Forensics
NIST Special Publication 800-101 Revision 1 Guidelines on Mobile Device Forensics Rick Ayers Sam Brothers Wayne Jansen http://dx.doi.org/10.6028/NIST.SP.800-101r1 NIST Special Publication 800-101 Revision 1 Guidelines on Mobile Device Forensics Rick Ayers Software and Systems Division Information Technology Laboratory Sam Brothers U.S. Customs and Border Protection Department of Homeland Security Springfield, VA Wayne Jansen Booz-Allen-Hamilton McLean, VA http://dx.doi.org/10.6028/NIST.SP. 800-101r1 May 2014 U.S. Department of Commerce Penny Pritzker, Secretary National Institute of Standards and Technology Patrick D. Gallagher, Under Secretary of Commerce for Standards and Technology and Director Authority This publication has been developed by NIST in accordance with its statutory responsibilities under the Federal Information Security Management Act of 2002 (FISMA), 44 U.S.C. § 3541 et seq., Public Law (P.L.) 107-347. NIST is responsible for developing information security standards and guidelines, including minimum requirements for Federal information systems, but such standards and guidelines shall not apply to national security systems without the express approval of appropriate Federal officials exercising policy authority over such systems. This guideline is consistent with the requirements of the Office of Management and Budget (OMB) Circular A-130, Section 8b(3), Securing Agency Information Systems, as analyzed in Circular A- 130, Appendix IV: Analysis of Key Sections. Supplemental information is provided in Circular A- 130, Appendix III, Security of Federal Automated Information Resources. Nothing in this publication should be taken to contradict the standards and guidelines made mandatory and binding on Federal agencies by the Secretary of Commerce under statutory authority. -

Cellular Network Sunsetting
Cellular Network Sunsetting By Dave Anderson, Senior IoCP Program Manager The use of acronyms by the cellular industry is extensive. 3GPP, 2G, 3G, 4G, 5G, LTE, CDMA, 1xRTT, HSPA, GPRS, EV-DO, GSM, NB-IoT, and many others are examples of the plethora of technologies and descriptions used to ultimately describe the actual hardware and service used by a device to connect to various networks to communicate information. This complexity pales in comparison to the FCC spectrum allocation chart shown in Fig 1. The chart depicts the frequency spectrums where toys, TV, radio, military, medical, marine radios, satellites, space telescopes and all the other frequency uses in the United States. Other countries have their own versions of this chart. Cellular technology utilizes a very small portion of this chart, yet occupies a large portion of everyday life in today’s connected society. Figure 1 Close examination of this chart will show that there are no open or available blocks of spectrum, so as new technologies are developed they must either layer on top of existing technologies, or aging technologies must be turned off or ‘sunset’ to free up spectrum for newer technologies. The cell phone industry has diligently worked to define a consumer market where the expectation is to replace this communication device with contract renewal type regularity. From a consumer point of view, the older technologies are usually long passed before a sunset event would force a phone upgrade. In parallel to the explosive cell phone market growth is the industrial usage of the cellular communication networks. The presence of a cellular network removes the necessity for wired connections and makes mobile monitoring possible for a number of industries. -

4G LTE Standards
Standard of 4G LTE Jia SHEN CAICT 1 Course Objectives: Evolution of LTE-Advanced LTE-Advanced pro 2 2 Evolution of LTE/LTE-A technology standard Peak rate LTE-Advanced 3Gbps R10 R11 R12 LTE • Distributed • D2D R9 antenna • TDD Flexible 300Mbps R8 • dual layer CoMP slot beamformi • Enhanced allocation ng • CA MIMO • 3D MIMO • Terminal • Enhanced • OFDM • Enhanced CA • … location MIMO • MIMO • … technology • Relay • … • HetNet 2008 2009 • … 2011 2012 2014 Terminal location technology dual layer3 beamforming CA Enhanced antenna Relay Course Objectives: Evolution of LTE-Advanced CA Enhanced MIMO CoMP eICIC Relay LTE-Advanced pro 4 4 Principle of carrier aggregation (CA) Carrier aggregation • In order to satisfy the design of LTE-A system with the maximum bandwidth of 100MHz, and to maintain the backward compatibility,3GPP proposed carrier aggregation. In the LTE-A system, the maximum bandwidth of a single carrier is 20MHz Participate in the aggregati on of the various LTE carrier is known as the LTE-A mem ber carrier (Component Car rier, CC) Standard Considering the backward compatibility of LTE system, the maximum bandwidth of a single carrier unit is 20M Hz in the LTE-A system. All carrier units will be designed to be compatible with LTE, but at this stage it does not exclude the considerati on of non - backward compatible carriers. In the LTE-A FDD system, the terminal can be configured to aggregate different bandwidth, different number o f carriers. For TDD LTE-A systems, the number of uplink and downlink carriers is the same in a typical scence. In the LTE-A system, CA supports up to 5 DL carriers. -

18-452/18-750 Wireless Networks and Applications Overview Cellular
Overview 18-452/18-750 Surveys Wireless Networks and Applications Cellular principles Lecture 17: » Cellular design Cellular - Principles » Elements of a cellular network » How does a mobile phone take place? Peter Steenkiste » Handoff » Frequency Allocation, Traffic Engineering Early cellular generations: 1G, 2G, 3G Spring Semester 2017 Today’s cellular: LTE http://www.cs.cmu.edu/~prs/wirelessS17/ Some slides based on material from “Wireless Communication Networks and Systems” © 2016 Pearson Higher Education, Inc. Peter A. Steenkiste, CMU 1 Peter A. Steenkiste, CMU 2 The Advent of Cellular versus WiFi Cellular Networks Cellular WiFi Mobile radio telephone system was based on: Licensed Unlicensed » Predecessor of today’s cellular systems Spectrum » High power transmitter/receivers Provisioned Unprovisioned » Could support about 25 channels Service model » in a radius of 80 Km “for pay” “free” – no SLA To increase network capacity: » Multiple lower power transmitters (100W or less) MAC services Fixed bandwidth Best effort » Smaller transmission radius -> area split in cells SLAs no SLAs » Each cell with its own frequencies and base station » Adjacent cells use different frequencies Implications for level of service (SLAs), cost, » The same frequency can be reused at sufficient distance nature of protocols, …? These trends are continuing … Peter A. Steenkiste, CMU 3 Peter A. Steenkiste, CMU 4 Page 1 The Cellular Idea The MTS network http://www.privateline.com/PCS/images/SaintLouis2.gif In December 1947 Donald H. Ring outlined the idea in a Bell labs memo Split an area into cells, each with their own low power towers Each cell would use its own frequency Did not take off due to “extreme-at-the-time” processing needs » Handoff for thousands of users » Rapid switching infeasible – maintain call while changing frequency » Technology not ready Peter A. -

Network Validation for CDMA 2000 1X EV-DO Technology Technical Handbook Report
2 3 4 5 Network Validation for CDMA 2000 1X EV-DO Technology Technical Handbook Report 6 6 In accordance to the requirements of the Request for Engineering, we carried out several information and asks in Panama, China, Sweden, USA, Norway, Finland, Korea and Taiwan. These locations are home to equipment suppliers, network operators or product regional representatives. The tasks outlined for compliance were defined as: 1- Revision, testing, analysis and recommendation of initial terminal equipment for use in the local IMT-2000 network. Compilation of accurate on the field information on troublesome equipment. 2- Secure availability of terminal equipment to synchronize with the new IMT-2000 platform. 3- Interpretation and recommendation of a product release information listing that will be able to interact with the majority of available terminals, particularly low- end supplies, without affecting GoS/QoS. 4- Cellular tests and measurements. Perform data throughput tests with terminals in working IMT-2000 networks. Sensitivity and Performance measurements. 5- Revision, testing, analysis and recommendation of testing equipment to be used for engineering purposes in the IMT-2000 network at terminal level (level 1,2,3) and network level. 6- Conduct laboratory testing and measurements on network equipment (including antennas) and terminals. 7- Purchasing of spare parts of key components of the IMT-2000 network. 8- Pursuing adequate training relevant to the technology and vendor for know-how transfer to network operator. 7 9- Testing and analysis of IMT-2000 networks in the countries visited with hardware and software tools. Network Validation for CDMA 2000 1X EV-DO Technology Technical Handbook Report 7 In meetings with manufacturers of IMT-2000 terminals were held, model compatibility was observed and technical training received by the manufacturers of equipment. -

Security Architecture in UMTS Third Generation Cellular Networks Tomás Balderas-Contreras René A
Security Architecture in UMTS Third Generation Cellular Networks Tomás Balderas-Contreras René A. Cumplido-Parra Reporte Técnico No. CCC-04-002 27 de febrero de 2004 © Coordinación de Ciencias Computacionales INAOE Luis Enrique Erro 1 Sta. Ma. Tonantzintla, 72840, Puebla, México. Security Architecture in UMTS Third Generation Cellular Networks Tom´asBalderas-Contreras Ren´eA. Cumplido-Parra Coordinaci´onde Ciencias Computacionales, Instituto Nacional de Astrof´ısica, Optica´ y Electr´onica, Luis Enrique Erro 1, Sta. Ma. Tonantzintla, 72840, Puebla, MEXICO [email protected] [email protected] Abstract Throughout the last years there has been a great interest in developing and standardizing the technologies needed to achieve high speed transmission of data in cellular networks. As a result, mobile communications technology has evolved amaz- ingly during the last decades to meet a very demanding market. Third generation (3G) wireless networks represent the more recent stage in this evolutionary process; they provide users with high transmission bandwidths which allow them to transmit both audio and video information in a secure manner. This report concerns a specific imple- mentation of the 3G requirement specification: Universal Mobile Telecommunications System (UMTS), which is considered to be the most important of the 3G proposals. In order to protect the information transmitted through the radio interface, either user data or signaling data, an advanced security scheme was conceived. Among the features of this scheme are: mutual authentication, -
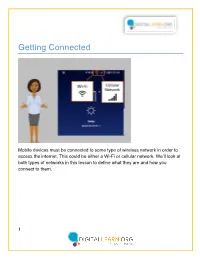
Getting Connected
Getting Connected Mobile devices must be connected to some type of wireless network in order to access the internet. This could be either a Wi-Fi or cellular network. We’ll look at both types of networks in this lesson to define what they are and how you connect to them. 1 A wi-fi network provides a wireless internet connection. All smartphones and tablets can connect to wi-fi. To set up a Wi-Fi network in your home, you must sign up with an Internet Service Provider, like your local phone or cable company. Many businesses, libraries, and other public places offer free wi-fi. Some businesses offer public Wi-Fi access for a small fee. You can use these public wi-fi networks while you visit these locations. 2 To connect to a Wi-Fi network for the first time, open your settings app. Then tap on Wi-Fi. It will show a list of any networks that are nearby. Networks with a lock icon require a password. This Network is Public Wi-Fi at a library and does not need a password. To access it, just tap the network name. Sometimes you may have to accept an agreement on public networks before you can continue. Once you’re connected, you’ll see the Wi-Fi icon in the status bar at the top of your device. 3 Always keep your information safe while connecting to Wi-Fi: Make sure you trust the public network before connecting to it. Do you know who set up the network? Try not to send private information over public Wi-Fi networks. -

Multimodem CDMA Datasheet: Cellular Modems
® MultiModem CDMA Benefits Cellular Modems • Rugged industrial chassis design • Desktop or panel mounting • Carrier approved • RS-232, USB and Ethernet interfaces The MultiModem® CDMA cellular modem offers standards-based dual-band CDMA2000 1xRTT performance. This ready-to-deploy, standalone modem provides wireless data communication and integrates seamlessly with virtually any application. It is available with a broad range of interface options including RS-232, USB and Ethernet to cover all of your application needs. The MultiModem CDMA cellular modem is based on industry-standard open interfaces and can be desktop or panel mounted. Features • CDMA2000 1xRTT • Qualcomm® MSM6050 chipset • CDMA IS-95A, IS-95B backwards compatible • Dual-band 800/1900 MHz CDMA • Packet data up to 153.6K bps forward and reverse • 14.4K bps circuit switched data • Short Message Services (SMS) • RS-232, USB and Ethernet interfaces • Models available with a complete TCP/IP stack • SMA antenna connector • Serial interface supports DTE speeds to 230K bps • AT command compatible • Numerous LEDs provide operational status • Over-the-Air activation • Desktop or panel mounting • CDG 1 and 2 network certified • Carrier approved • Two-year warranty Voice Features. The MultiModem CDMA cellular modem Highlights provides telephony and Dual Tone Multi Frequency (DTMF) Applications. With packet data speeds up to 153.6K bps, functionality, as well as, AMPS Voice, QCELP (13K) and echo the MultiModem CDMA cellular modem is targeted at cancellation. applications which periodically need to send or receive data over a wireless network. It is ideal for: Compatible Supplementary Services. The MultiModem CDMA cellular modem is compatible with supplementary services • Automated machine-to-machine (M2M) such as call forwarding, call barring, multiparty, call waiting • Public Safety/Emergency Services and call hold, calling line identification, closed user group • Public Transit and call transfer. -

Cellular Wireless Networks Principles of Cellular Networks
Cellular Wireless Networks • Chapter 14 CS420/520 Axel Krings Page 1 Sequence 14 Principles of Cellular Networks • Underlying technology for mobile phones, personal communication systems, wireless networking etc. • Developed for mobile radio telephone — Replace high power transmitter/receiver systems • Typical support for 25 channels over 80km — Use lower power, shorter range, more transmitters CS420/520 Axel Krings Page 2 Sequence 14 1 Cellular Network Organization • Multiple low power transmitters — 100W or less • Area divided into cells — Each with own antenna — Each with own range of frequencies — Served by base station • Transmitter, receiver, control unit — Adjacent cells on different frequencies to avoid crosstalk CS420/520 Axel Krings Page 3 Sequence 14 Shape of Cells • Square — Width d cell has four neighbors at distance d and four at distance 2 d — Better if all adjacent antennas equidistant • Simplifies choosing and switching to new antenna • Hexagon — Provides equidistant antennas — Radius defined as radius of circum-circle • Distance from center to vertex equals length of side — Distance between centers of cells radius R is 3 R — Not always precise hexagons • Topographical limitations • Local signal propagation conditions • Location of antennas CS420/520 Axel Krings Page 4 Sequence 14 2 Cellular Geometries CS420/520 Axel Krings Page 5 Sequence 14 Frequency Reuse • Power of base transceiver controlled — Allow communications within cell on given frequency — Limit escaping power to adjacent cells — Allow re-use of frequencies -

Road Traffic Estimation Using Cellular Network Signaling in Intelligent Transportation Systems
Road Traffic Estimation using Cellular Network Signaling in Intelligent Transportation Systems David Gundlegård and Johan M Karlsson Linköping University Post Print N.B.: When citing this work, cite the original article. Original Publication: David Gundlegård and Johan M Karlsson, Road Traffic Estimation using Cellular Network Signaling in Intelligent Transportation Systems, 2009, Wireless technologies in Intelligent Transportation Systems. Editors: Ming-Tuo Zhou, Yan Zhang and L. T. Yan. ISBN: 978-1-60741-588-6 Copyright: Nova Science Publishers https://www.novapublishers.com/ Postprint available at: Linköping University Electronic Press http://urn.kb.se/resolve?urn=urn:nbn:se:liu:diva-50734 In: Wireless Technologies in Intelligent Transportation Systems ISBN 978-1-60741-588-6 Editors: Ming-Tuo Zhou, Yan Zhang and L. T. Yan, pp. © 2009 Nova Science Publishers, Inc. Chapter 13 ROAD TRAFFIC ESTIMATION USING CELLULAR NETWORK SIGNALING IN INTELLIGENT TRANSPORTATION SYSTEMS David Gundlegård and Johan M Karlsson Department of Science and Technology Linköping University, 601 74 Norrköping ABSTRACT In the area of Intelligent Transportation Systems the introduction of wireless communications is reshaping the information distribution concept, and is one of the most important enabling technologies. The distribution of real-time traffic information, scheduling and route-guidance information is helping the transportation management systems in their strive to optimize the system. The communication required to transfer all this information is rather expensive in terms of transmission power, use of the scarce resources of frequencies and also the building of an infrastructure to support the transceivers. By using information that already exists and is exchanged within the infrastructures of the GSM and UMTS networks, a lot of the resource problems are solved.