Game Playing Ch
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
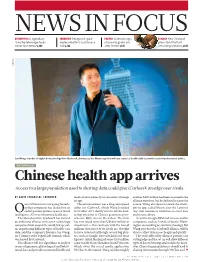
Chinese Health App Arrives Access to a Large Population Used to Sharing Data Could Give Icarbonx an Edge Over Rivals
NEWS IN FOCUS ASTROPHYSICS Legendary CHEMISTRY Deceptive spice POLITICS Scientists spy ECOLOGY New Zealand Arecibo telescope faces molecule offers cautionary chance to green UK plans to kill off all uncertain future p.143 tale p.144 after Brexit p.145 invasive predators p.148 ICARBONX Jun Wang, founder of digital biotechnology firm iCarbonX, showcases the Meum app that will use reams of health data to provide customized medical advice. BIOTECHNOLOGY Chinese health app arrives Access to a large population used to sharing data could give iCarbonX an edge over rivals. BY DAVID CYRANOSKI, SHENZHEN medical advice directly to consumers through another $400 million had been invested in the an app. alliance members, but he declined to name the ne of China’s most intriguing biotech- The announcement was a long-anticipated source. Wang also demonstrated the smart- nology companies has fleshed out an debut for iCarbonX, which Wang founded phone app, called Meum after the Latin for earlier quixotic promise to use artificial in October 2015 shortly after he left his lead- ‘my’, that customers would use to enter data Ointelligence (AI) to revolutionize health care. ership position at China’s genomics pow- and receive advice. The Shenzhen firm iCarbonX has formed erhouse, BGI, also in Shenzhen. The firm As well as Google, IBM and various smaller an ambitious alliance with seven technology has now raised more than US$600 million in companies, such as Arivale of Seattle, Wash- companies from around the world that special- investment — this contrasts with the tens of ington, are working on similar technology. But ize in gathering different types of health-care millions that most of its rivals are thought Wang says that the iCarbonX alliance will be data, said the company’s founder, Jun Wang, to have invested (although several big play- able to collect data more cheaply and quickly. -

Fml-Based Dynamic Assessment Agent for Human-Machine Cooperative System on Game of Go
Accepted for publication in International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems in July, 2017 FML-BASED DYNAMIC ASSESSMENT AGENT FOR HUMAN-MACHINE COOPERATIVE SYSTEM ON GAME OF GO CHANG-SHING LEE* MEI-HUI WANG, SHENG-CHI YANG Department of Computer Science and Information Engineering, National University of Tainan, Tainan, Taiwan *[email protected], [email protected], [email protected] PI-HSIA HUNG, SU-WEI LIN Department of Education, National University of Tainan, Tainan, Taiwan [email protected], [email protected] NAN SHUO, NAOYUKI KUBOTA Dept. of System Design, Tokyo Metropolitan University, Japan [email protected], [email protected] CHUN-HSUN CHOU, PING-CHIANG CHOU Haifong Weiqi Academy, Taiwan [email protected], [email protected] CHIA-HSIU KAO Department of Computer Science and Information Engineering, National University of Tainan, Tainan, Taiwan [email protected] Received (received date) Revised (revised date) Accepted (accepted date) In this paper, we demonstrate the application of Fuzzy Markup Language (FML) to construct an FML- based Dynamic Assessment Agent (FDAA), and we present an FML-based Human–Machine Cooperative System (FHMCS) for the game of Go. The proposed FDAA comprises an intelligent decision-making and learning mechanism, an intelligent game bot, a proximal development agent, and an intelligent agent. The intelligent game bot is based on the open-source code of Facebook’s Darkforest, and it features a representational state transfer application programming interface mechanism. The proximal development agent contains a dynamic assessment mechanism, a GoSocket mechanism, and an FML engine with a fuzzy knowledge base and rule base. -

When Are We Done with Games?
When Are We Done with Games? Niels Justesen Michael S. Debus Sebastian Risi IT University of Copenhagen IT University of Copenhagen IT University of Copenhagen Copenhagen, Denmark Copenhagen, Denmark Copenhagen, Denmark [email protected] [email protected] [email protected] Abstract—From an early point, games have been promoted designed to erase particular elements of unfairness within the as important challenges within the research field of Artificial game, the players, or their environments. Intelligence (AI). Recent developments in machine learning have We take a black-box approach that ignores some dimensions allowed a few AI systems to win against top professionals in even the most challenging video games, including Dota 2 and of fairness such as learning speed and prior knowledge, StarCraft. It thus may seem that AI has now achieved all of focusing only on perceptual and motoric fairness. Additionally, the long-standing goals that were set forth by the research we introduce the notions of game extrinsic factors, such as the community. In this paper, we introduce a black box approach competition format and rules, and game intrinsic factors, such that provides a pragmatic way of evaluating the fairness of AI vs. as different mechanical systems and configurations within one human competitions, by only considering motoric and perceptual fairness on the competitors’ side. Additionally, we introduce the game. We apply these terms to critically review the aforemen- notion of extrinsic and intrinsic factors of a game competition and tioned AI achievements and observe that game extrinsic factors apply these to discuss and compare the competitions in relation are rarely discussed in this context, and that game intrinsic to human vs. -

About Go, the Ancient Game in Which AI Bested a Master 10 March 2016, by Youkyung Lee
All about Go, the ancient game in which AI bested a master 10 March 2016, by Youkyung Lee ___ WHAT IS GO? In Go, also known as baduk in Korean and weiqi in Chinese, two players take turns putting black or white stones on a 19-by-19 square grid. The goal: to put more territory under one's control by surrounding vacant areas with the stones. Many Asian people see it as not just a game but also a reflection of life, one's personality and temper. There are nearly infinite ways to play Go, South Korean professional Go player Lee Sedol, right, and each player has his or her distinctive style. appears on the screen during the second match of the That's partly the reason the game has been Google DeepMind Challenge Match against Google's particularly difficult for artificial intelligence to artificial intelligence program, AlphaGo at the media master. room in Seoul, South Korea, Thursday, March 10, 2016. Google's computer program AlphaGo defeated its human opponent, South Korean Go champion Lee Sedol, on Wednesday in the first face-off of a historic five-game match. (AP Photo/Lee Jin-man) The rules of Go, the ancient Chinese board game that is the stage for a man-vs-machine battle this week, are beautifully simple. Actually playing it is anything but. Go is considered to be far more complex than chess, making it remarkable that a cutting-edge computer program by Google has swept the first two games of a five-game match against a human South Korean professional Go player Lee Sedol, right, Go champion, Lee Sedol. -

Mastering the Game of Go Without Human Knowledge
Mastering the Game of Go without Human Knowledge David Silver*, Julian Schrittwieser*, Karen Simonyan*, Ioannis Antonoglou, Aja Huang, Arthur Guez, Thomas Hubert, Lucas Baker, Matthew Lai, Adrian Bolton, Yutian Chen, Timothy Lillicrap, Fan Hui, Laurent Sifre, George van den Driessche, Thore Graepel, Demis Hassabis. DeepMind, 5 New Street Square, London EC4A 3TW. *These authors contributed equally to this work. A long-standing goal of artificial intelligence is an algorithm that learns, tabula rasa, su- perhuman proficiency in challenging domains. Recently, AlphaGo became the first program to defeat a world champion in the game of Go. The tree search in AlphaGo evaluated posi- tions and selected moves using deep neural networks. These neural networks were trained by supervised learning from human expert moves, and by reinforcement learning from self- play. Here, we introduce an algorithm based solely on reinforcement learning, without hu- man data, guidance, or domain knowledge beyond game rules. AlphaGo becomes its own teacher: a neural network is trained to predict AlphaGo’s own move selections and also the winner of AlphaGo’s games. This neural network improves the strength of tree search, re- sulting in higher quality move selection and stronger self-play in the next iteration. Starting tabula rasa, our new program AlphaGo Zero achieved superhuman performance, winning 100-0 against the previously published, champion-defeating AlphaGo. Much progress towards artificial intelligence has been made using supervised learning sys- tems that are trained to replicate the decisions of human experts 1–4. However, expert data is often expensive, unreliable, or simply unavailable. Even when reliable data is available it may impose a ceiling on the performance of systems trained in this manner 5. -

Mastering the Game of Go Without Human Knowledge
ArtICLE doi:10.1038/nature24270 Mastering the game of Go without human knowledge David Silver1*, Julian Schrittwieser1*, Karen Simonyan1*, Ioannis Antonoglou1, Aja Huang1, Arthur Guez1, Thomas Hubert1, Lucas Baker1, Matthew Lai1, Adrian Bolton1, Yutian Chen1, Timothy Lillicrap1, Fan Hui1, Laurent Sifre1, George van den Driessche1, Thore Graepel1 & Demis Hassabis1 A long-standing goal of artificial intelligence is an algorithm that learns, tabula rasa, superhuman proficiency in challenging domains. Recently, AlphaGo became the first program to defeat a world champion in the game of Go. The tree search in AlphaGo evaluated positions and selected moves using deep neural networks. These neural networks were trained by supervised learning from human expert moves, and by reinforcement learning from self-play. Here we introduce an algorithm based solely on reinforcement learning, without human data, guidance or domain knowledge beyond game rules. AlphaGo becomes its own teacher: a neural network is trained to predict AlphaGo’s own move selections and also the winner of AlphaGo’s games. This neural network improves the strength of the tree search, resulting in higher quality move selection and stronger self-play in the next iteration. Starting tabula rasa, our new program AlphaGo Zero achieved superhuman performance, winning 100–0 against the previously published, champion-defeating AlphaGo. Much progress towards artificial intelligence has been made using trained solely by selfplay reinforcement learning, starting from ran supervised learning systems that are trained to replicate the decisions dom play, without any supervision or use of human data. Second, it of human experts1–4. However, expert data sets are often expensive, uses only the black and white stones from the board as input features. -

FML-Based Prediction Agent and Its Application to Game of Go
Published as a conference paper at IFSA-SCIS 2017______________________________________________________________________ FML-based Prediction Agent and Its Application to Game of Go Chang-Shing Lee Chia-Hsiu Kao Yusuke Nojima Nan Shuo Mei-Hui Wang Sheng-Chi Yang Ryosuke Saga Naoyuki Kubota Dept. of Computer Science and Information Engineering Dept. of Electrical Engineering Dept. of System Design Knowledge Application and Web Service Research Center and Information Science Tokyo Metropolitan University National University of Tainan Osaka Prefecture University Tokyo, Japan Tainan, Taiwan Osaka, Japan [email protected] [email protected] [email protected] Abstract- In this paper, we present a robotic prediction agent Many different real-world applications are with a high-level including a darkforest Go engine, a fuzzy markup language (FML) of uncertainty. A lot of researches proved the good performance assessment engine, an FML-based decision support engine, and a of using fuzzy sets. Being an IEEE Standard in May 2016, fuzzy robot engine for game of Go application. The knowledge base and markup language (FML) provides designers of intelligent rule base of FML assessment engine are constructed by referring decision making systems with a unified and high-level the information from the darkforest Go engine located in NUTN methodology for describing systems’ behaviors by means of and OPU, for example, the number of MCTS simulations and rules based on human domain knowledge [10, 11]. The main winning rate prediction. The proposed robotic prediction agent advantage of using FML is easy to understand and extend the first retrieves the database of Go competition website, and then the implemented programs for other researchers. -

Alphago Program, What New Ideas from Sedol Do Foresee?
Pickford Film Center DOCTOBER DOCUMENTARY FILM FESTIVAL, 2017 Film Discussion Guide ALPHA GO (2017) A documentary film by Greg Kohl https://www.mountainfilm.org/festival/personalities/greg-kohs THE STORY: “The ancient Chinese board game Go has long been considered the holy-grail for artificial intelligence. Its simple rules but near-infinite number of outcomes make it exponentially more complex than chess. Mastery of the game by computers was considered by expert players and the AI community alike to be out of reach for at least another decade. Yet in 2016, Google's DeepMind team announced that they would be taking on Lee Sedol, the world's most elite Go champion. The match was set for a weeklong tournament in Seoul in early 2016, and there was more at stake than the million-dollar prize. Director Greg Kohs' absorbing documentary chronicles Google's DeepMind team as it prepares to test the limits of its rapidly evolving AI technology. The film pits machine against man, and reveals as much about the workings of the human mind as it does the future of AI.” —Ian Hollander THE CAST: Frank Lantz, Director, New York University Game Center Demis Hassabis, Co-Founder and CEO, DeepMind Shane Legg, Co-Founder and Chief Scientist, DeepMind David Silver, Lead Researcher, DeepMind Lee Sedol, 9p World GO Professional Aja Hung, Lead Programmer, DeepMind Fan Hui, 2p Go Professional, European Go Champion Janice Kim, 3p Go Professional Andrew Jackson, Vice President Operations, American GO Association Yuan Zhou, 7p Go Professional Julian Schrittweiser, Software Engineer, DeepMind DOCUMENTARY STYLE: Bill Nichols, film educator, has written many texts on documentary styles and his analysis is distilled in the article cited here. -
![Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm Arxiv:1712.01815V1 [Cs.AI] 5 Dec 2017](https://docslib.b-cdn.net/cover/5893/mastering-chess-and-shogi-by-self-play-with-a-general-reinforcement-learning-algorithm-arxiv-1712-01815v1-cs-ai-5-dec-2017-10355893.webp)
Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm Arxiv:1712.01815V1 [Cs.AI] 5 Dec 2017
Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm David Silver,1∗ Thomas Hubert,1∗ Julian Schrittwieser,1∗ Ioannis Antonoglou,1 Matthew Lai,1 Arthur Guez,1 Marc Lanctot,1 Laurent Sifre,1 Dharshan Kumaran,1 Thore Graepel,1 Timothy Lillicrap,1 Karen Simonyan,1 Demis Hassabis1 1DeepMind, 6 Pancras Square, London N1C 4AG. ∗These authors contributed equally to this work. Abstract The game of chess is the most widely-studied domain in the history of artificial intel- ligence. The strongest programs are based on a combination of sophisticated search tech- niques, domain-specific adaptations, and handcrafted evaluation functions that have been refined by human experts over several decades. In contrast, the AlphaGo Zero program recently achieved superhuman performance in the game of Go, by tabula rasa reinforce- ment learning from games of self-play. In this paper, we generalise this approach into a single AlphaZero algorithm that can achieve, tabula rasa, superhuman performance in many challenging domains. Starting from random play, and given no domain knowledge except the game rules, AlphaZero achieved within 24 hours a superhuman level of play in the games of chess and shogi (Japanese chess) as well as Go, and convincingly defeated a world-champion program in each case. arXiv:1712.01815v1 [cs.AI] 5 Dec 2017 The study of computer chess is as old as computer science itself. Babbage, Turing, Shan- non, and von Neumann devised hardware, algorithms and theory to analyse and play the game of chess. Chess subsequently became the grand challenge task for a generation of artificial intel- ligence researchers, culminating in high-performance computer chess programs that perform at superhuman level (9, 13). -

How the Computer Beat the Go Player
CONSCIOUSNESS REDUX MACHINE LEARNING How the Computer Beat the Go Player As a leading go player falls to a machine, artificial intelligence takes a decisive step on the road to overtaking the natural variety God moves the player, he in turn, the piece. But what god beyond God begins the round of dust and time and sleep and agonies? —Jorge Luis Borges, from “Chess,” 1960 The victory in March of the computer program AlphaGo over one of the world’s top handful of go players marks the high- est accomplishment to date for the bur- era is over, and a new one has begun. The reigning world chess champion Garry geoning field of machine learning and methods underlying AlphaGo, and its Kasparov. In a six-game match played in intelligence. The computer beat Lee Se- recent victory, have startling implications 1996, Kaspa rov prevailed against Deep dol at go, a very old and traditional board for the future of machine intelligence. Blue by three wins, two draws and one game, at a highly publicized tournament loss but lost a year later in a historic re- in Seoul in a 4–1 rout. With this defeat, Coming Out of Nowhere match 3.5 to 2.5. (Scoring rules permit ) computers have bettered people in the The ascent of AlphaGo to the top of the half points in the case of a draw.) last of the classical board games, this one go world has been stunning and quite dis- Chess is a classic game of strategy, Koch known for its depth and simplicity. -

Deep Reinforcement Learning: a Brief Introduction
Deep Reinforcement Learning: a brief introduction (Copyright © 2018 Piero Scaruffi - Silicon Valley Artificial Intelligence Research Institute) The game of go/weichi had been a favorite field of research since the birth of deep learning. In 2006 Remi Coulom in France applied Ulam's old Monte Carlo method to the problem of searching a tree data structure (one of the most common problems in computational math, but particularly difficult when the data are game moves), and thus obtained the Monte Carlo Tree Search algorithm, and then applied it to go/weichi ("Bandit Based Monte-Carlo Planning", 2006). At the same time Levente Kocsis and Csaba Szepesvari developed the UCT algorithm (Upper Confidence Bounds for Trees algorithm), an application of the bandit algorithm to the Monte Carlo search, the bandit algorithm being a problem in probability theory first studied by Herbert Robbins in 1952 at the Institute for Advanced Study ("Some aspects of the sequential design of experiments", 1952). These algorithms dramatically improved the chances by machines to beat go masters: in 2009 Fuego Go (developed at the University of Alberta) beat Zhou Junxun, in 2010 MogoTW (developed by a French-Taiwanese team) beat Catalin Taranu, in 2012 Tencho no Igo/ Zen (developed by Yoji Ojima) beat Takemiya Masaki, in 2013 Crazy Stone (by Remi Coulom) beat Yoshio Ishida, and in 2016 AlphaGo (developed by Google's DeepMind) beat Lee Sedol. DeepMind's victory was widely advertised. DeepMind used a slightly modified Monte Carlo algorithm but, more importantly, AlphaGo taught itself by playing against itself. AlphaGo's neural network was trained with 150,000 games played by go/weichi masters. -

Algorithmic Business & the Pursuit of Digital Happiness
Algorithmic business & The pursuit of digital Happiness Algorithmic Business In Code We Trust Onlife: Dealing with iGen Design for Happiness http://labs.sogeti.com/research the dawn of algorithmic business (in the age of customer obsession where you are either predator or prey) DIGITAL FUNDAMENTALLY CHANGES THE RELATIONSHIP WITH CUSTOMERS (RE-ENGINEER HOW BUSINESS CREATES VALUE IN THE DIGITAL AGE) USE DIGITAL TO HELP CUSTOMERS GET TO THE OUTCOMES THEY DESIRE (EXPAND YOUR ROLE IN THE PERSONAL VALUE ECOSYSTEM OF YOUR CUSTOMER) NOT JUST DCX (OPERATIONAL AGILITY - SPEED TO MARKET - EMPLOYEE PRODUCTIVITY - LEANER PROCESSES - MAXIMISE ASSET UTILISATION) INNOVATE AT THE SPEED OF TECHNOLOGY CHANGE (AND ADOPTION BY THE CONSUMER) Big Bang Market Number of Adopters Late Majority Late Early Majority Early Laggards REDUCE Adopters Early THE RISK OF NEW BEHAVIOURS AND Innovators PEOPLE WILL ADOPT THEM MORE QUICKLY Trial Users ‘Everybody’ Time to adopt V I N T | Vision • Inspiration • Navigation • Trends 900m No Yes My customer is changing faster than my organisation Jack Welsch “If the rate of change on the outside exceeds the rate of change on the inside, the end is near” Machine Platform Crowd Innovate at the speed of Technology Change Machine 1 October 2015 - alpha Go vs Fan Hui 5 - 0 March 2016 - alpha go vs Lee Sedol 4 - 1 mAY 2017 - ALPHA GO MASTER VS KE JIE 3 - 0 23-27 May 2017 - Ke Jie versus AlphaGo Master 1 AI FIRST: LEARNING FROM THE COMPUTER In 2013, Google’s parent company, Alphabet, purchased the British company DeepMind for more than 600 million dollars. This is a start-up specialized in artificial intelligence.