Theoretical and Experimental Study of the Regioselectivity of Michael Additions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Catalytic Direct Asymmetric Michael Reactions
ORGANIC LETTERS 2001 Catalytic Direct Asymmetric Michael Vol. 3, No. 23 Reactions: Taming Naked Aldehyde 3737-3740 Donors Juan M. Betancort and Carlos F. Barbas III* The Skaggs Institute for Chemical Biology and the Department of Molecular Biology, The Scripps Research Institute, 10550 North Torrey Pines Road, La Jolla, California 92037 [email protected] Received September 5, 2001 ABSTRACT Direct catalytic enantio- and diastereoselective Michael addition reactions of unmodified aldehydes to nitro olefins using (S)-2-(morpholinomethyl)- pyrrolidine as a catalyst are described. The reactions proceed in good yield (up to 96%) in a highly syn-selective manner (up to 98:2) with enantioselectivities approaching 80%. The resulting γ-formyl nitro compounds are readily converted to chiral, nonracemic 3,4-disubstituted pyrrolidines. The Michael reaction is generally regarded as one of the Typically, carbon nucleophiles that contain an active most efficient carbon-carbon bond forming reactions, and methylene center such as malonic acid esters, â-keto esters, studies concerning this reaction have played an important nitroalkanes, etc. have been studied in the Michael reaction. role in the development of modern synthetic organic Carbonyl compounds, and ketones in particular, have gener- chemistry.1 As the demand for optically active compounds ally only been used as donors following their preactivation has soared in recent years, much progress has been made in by conversion into a more reactive species such as enol or the development of asymmetric variants of this reaction, enamine equivalents.5,6 In these cases, additional synthetic providing for the preparation of Michael adducts with high enantiomeric purity.2 Though remarkable advances have been (3) (a) Chataigner, I.; Gennari, C.; Ongeri, S.; Piarulli, U.; Ceccarelli, S. -

Proton Nmr Spectroscopy
1H NMR Spectroscopy (#1c) The technique of 1H NMR spectroscopy is central to organic chemistry and other fields involving analysis of organic chemicals, such as forensics and environmental science. It is based on the same principle as magnetic resonance imaging (MRI). This laboratory exercise reviews the principles of interpreting 1H NMR spectra that you should be learning right now in Chemistry 302. There are four questions you should ask when you are trying to interpret an NMR spectrum. Each of these will be discussed in detail. The Four Questions to Ask While Interpreting Spectra 1. How many different environments are there? The number of peaks or resonances (signals) in the spectrum indicates the number of nonequivalent protons in a molecule. Chemically equivalent protons (magnetically equivalent protons) give the same signal in the NMR whereas nonequivalent protons give different signals. 1 For example, the compounds CH3CH3 and BrCH2CH2Br all have one peak in their H NMR spectra because all of the protons in each molecule are equivalent. The compound below, 1,2- dibromo-2-methylpropane, has two peaks: one at 1.87 ppm (the equivalent CH3’s) and the other at 3.86 ppm (the CH2). 1.87 1.87 ppm CH 3 3.86 ppm Br Br CH3 1.87 ppm 3.86 10 9 8 7 6 5 4 3 2 1 0 2. How many 1H are in each environment? The relative intensities of the signals indicate the numbers of protons that are responsible for individual signals. The area under each peak is measured in the form of an integral line. -
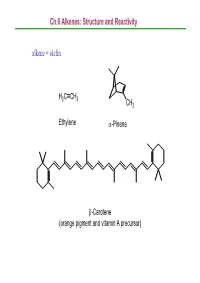
Ch.6 Alkenes: Structure and Reactivity Alkene = Olefin
Ch.6 Alkenes: Structure and Reactivity alkene = olefin H2CCH2 CH3 Ethylene α-Pinene β-Carotene (orange pigment and vitamin A precursor) Ch.6 Alkenes: Structure and Reactivity 6.1 Industrial Preparation and Use of Alkenes Compounds derived industrially from ethylene CH3CH2OH Ethanol CH3CHO Acetaldehyde CH3COOH Acetic acid HOCH2CH2OH Ethylene glycol ClCH2CH2Cl Ethylene dichloride H C=CHCl Vinyl chloride H2CCH2 2 O Ethylene oxide Ethylene (26 million tons / yr) O Vinyl acetate O Polyethylene Ch.6 Alkenes: Structure and Reactivity Compounds derived industrially from propylene OH Isopropyl alcohol H3CCH3 O Propylene oxide CH3 H3CCH CH2 Propylene Cumene (14 million tons / yr) CH3 CH3 Polypropylene Ch.6 Alkenes: Structure and Reactivity • Ethylene, propylene, and butene are synthesized industrially by thermal cracking of natural gas (C1-C4 alkanes) and straight-run gasoline (C4-C8 alkanes). 850-900oC CH (CH ) CH H + CH + H C=CH + CH CH=CH 3 2 n 3 steam 2 4 2 2 3 2 + CH3CH2CH=CH2 - the exact processes are complex; involve radical process H 900oC CH3CH2 CH2CH3 22H2CCH H2C=CH2 +H2 Ch.6 Alkenes: Structure and Reactivity • Thermal cracking is an example of a reaction whose energetics are dominated by entropy (∆So) rather than enthalpy (∆Ho) in the free-energy equation (∆Go = ∆Ho -T∆So) . ; C-C bond cleavage (positive ∆Ho) ; high T and increased number of molecules → larger T∆So Ch.6 Alkenes: Structure and Reactivity 6.2 Calculating Degree of Unsaturation unsaturated: formula of alkene CnH2n ; formula of alkane CnH2n+2 in general, each ring or double -

Ganic Compounds
6-1 SECTION 6 NOMENCLATURE AND STRUCTURE OF ORGANIC COMPOUNDS Many organic compounds have common names which have arisen historically, or have been given to them when the compound has been isolated from a natural product or first synthesised. As there are so many organic compounds chemists have developed rules for naming a compound systematically, so that it structure can be deduced from its name. This section introduces this systematic nomenclature, and the ways the structure of organic compounds can be depicted more simply than by full Lewis structures. The language is based on Latin, Greek and German in addition to English, so a classical education is beneficial for chemists! Greek and Latin prefixes play an important role in nomenclature: Greek Latin ½ hemi semi 1 mono uni 1½ sesqui 2 di bi 3 tri ter 4 tetra quadri 5 penta quinque 6 hexa sexi 7 hepta septi 8 octa octo 9 ennea nona 10 deca deci Organic compounds: Compounds containing the element carbon [e.g. methane, butanol]. (CO, CO2 and carbonates are classified as inorganic.) See page 1-4. Special characteristics of many organic compounds are chains or rings of carbon atoms bonded together, which provides the basis for naming, and the presence of many carbon- hydrogen bonds. The valency of carbon in organic compounds is 4. Hydrocarbons: Compounds containing only the elements C and H. Straight chain hydrocarbons are named according to the number of carbon atoms: CH4, methane; C2H6 or H3C-CH3, ethane; C3H8 or H3C-CH2-CH3, propane; C4H10 or H3C-CH2- CH2-CH3, butane; C5H12 or CH3CH2CH2CH2CH3, pentane; C6H14 or CH3(CH2)4CH3, hexane; C7H16, heptane; C8H18, octane; C9H20, nonane; C10H22, CH3(CH2)8CH3, decane. -

Surface Chemistry Changes of Weathered HDPE/Wood-Flour
Polymer Degradation and Stability 86 (2004) 1–9 www.elsevier.com/locate/polydegstab Surface chemistry changes of weathered HDPE/wood-flour composites studied by XPS and FTIR spectroscopy* Nicole M. Starka,), Laurent M. Matuanab aU.S. Department of Agriculture, Forest Service, Forest Products Laboratory, One Gifford Pinchot Drive, Madison, WI 53726-2398, United States bDepartment of Forestry, Michigan State University, East Lansing, MI 48824-1222, United States Received 7 August 2003; received in revised form 3 November 2003; accepted 4 November 2003 Abstract The use of wood-derived fillers by the thermoplastic industry has been growing, fueled in part by the use of wood-fiber– thermoplastic composites by the construction industry. As a result, the durability of wood-fiber–thermoplastic composites after ultraviolet exposure has become a concern. Samples of 100% high-density polyethylene (HDPE) and HDPE filled with 50% wood- flour (WF) were weathered in a xenon arc-type accelerated weathering apparatus for 2000 h. Changes in surface chemistry were studied using spectroscopic techniques. X-ray photoelectron spectroscopy (XPS) was used to verify the occurrence of surface oxidation. Fourier transform infrared (FTIR) spectroscopy was used to monitor the development of degradation products, such as carbonyl groups and vinyl groups, and to determine changes in HDPE crystallinity. The results indicate that surface oxidation occurred immediately after exposure for both the neat HDPE and WF/HDPE composites; the surface of the WF/HDPE composites was oxidized to a greater extent than that of the neat HDPE. This suggests that the addition of WF to the HDPE matrix results in more weather-related damage. -

Novel Poly(Vinyl Alcohol)-Based Column Coating for Capillary Electrophoresis of Proteins
Biochemical Engineering Journal 53 (2010) 137–142 Contents lists available at ScienceDirect Biochemical Engineering Journal journal homepage: www.elsevier.com/locate/bej Novel poly(vinyl alcohol)-based column coating for capillary electrophoresis of proteins Liang Xu, Xiao-Yan Dong, Yan Sun ∗ Department of Biochemical Engineering and Key Laboratory of Systems Bioengineering of the Ministry of Education, School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China article info abstract Article history: A novel and simple method for the preparation of chemically bonded poly(vinyl alcohol) (PVA) coat- Received 30 June 2010 ing to silica capillary inner wall was developed, and the PVA-coated capillary columns were employed Received in revised form for capillary electrophoresis (CE). The coating procedure included pretreatment of the capillary inner 30 September 2010 wall, silanization, aldehyde group functionalization and PVA immobilization. Electroosmotic flow of the Accepted 6 October 2010 coated capillary was almost suppressed over a wide pH range (pH 3–10). High-efficiency separations of cationic proteins (including cytochrome c, lysozyme, ␣-chymotrypsinogen A) at pH 3.0–5.0 and of anionic proteins (including myoglobin and trypsin inhibitor) at pH 10.0 were achieved with the PVA-coated cap- Keywords: Protein illary. Moreover, a “dual-opposite-injection” approach was adopted for simultaneous separations of both Separation cationic and anionic proteins at neutral pH with the prepared column. In this CE mode, positively charged Bioprocess Monitoring proteins migrated from one end of the column to the detector while negatively charged proteins from Adsorption the other end to the detection window. Good run-to-run repeatability was obtained in all of the protein Capillary electrophoresis CE separations performed in this work. -

Alkynes: Molecular and Structural Formulas
Alkynes: Molecular and Structural Formulas The alkynes comprise a series of carbon- and hydrogen-based compounds that contain at least one triple bond. This group of compounds is a homologous series with the general molecular formula of C n H2 n--2 , where n equals any integer greater than one. The simplest alkyne, ethyne (also known as acetylene), has two carbon atoms and the molecular formula of C2H2. The structural formula for ethyne is In longer alkyne chains, the additional carbon atoms are attached to each other by single covalent bonds. Each carbon atom is also attached to sufficient hydrogen atoms to produce a total of four single covalent bonds about itself. In alkynes of four or more carbon atoms, the triple bond can be located in different positions along the chain, leading to the formation of structural isomers. For example, the alkyne of molecular formula C4H6 has two isomers, Although alkynes possess restricted rotation due to the triple bond, they do not have stereoisomers like the alkenes because the bonding in a carbon-carbon triple bond is sp hybridized. In sp hybridization, the maximum separation between the hybridized orbitals is 180°, so the molecule is linear. Thus, the substituents on triple-bonded carbons are positioned in a straight line, and stereoisomers are impossible Alkynes: Nomenclature Although some common alkyne names, such as acetylene, are still found in many textbooks, the International Union of Pure and Applied Chemistry (IUPAC) nomenclature is required for journal articles. The rules for alkynes in this system are identical with those for alkenes, except for the ending. -

Recoverable Phospha-Michael Additions Catalyzed by a 4-N,N
molecules Article Recoverable Phospha-Michael Additions Catalyzed by a 4-N,N-Dimethylaminopyridinium Saccharinate Salt or a Fluorous Long-Chained Pyridine: Two Types of Reusable Base Catalysts Eskedar Tessema 1,†, Vijayanath Elakkat 1,† , Chiao-Fan Chiu 2,3,*, Jing-Hung Zheng 1, Ka Long Chan 1, Chia-Rui Shen 4,5, Peng Zhang 6,* and Norman Lu 1,7,* 1 Institute of Organic and Polymeric Materials, National Taipei University of Technology, Taipei 106, Taiwan; [email protected] (E.T.); [email protected] (V.E.); [email protected] (J.-H.Z.); [email protected] (K.L.C.) 2 Department of Pediatrics, Linkou Medical Center, Chang Gung Memorial Hospital, Taoyuan 333, Taiwan 3 Graduate Institute of Clinical Medical Sciences, College of Medicine, Chang Gung University, Taoyuan 333, Taiwan 4 Department of Medical Biotechnology and Laboratory Sciences, College of Medicine, Chang Gung University, Taoyuan 333, Taiwan; [email protected] 5 Department of Ophthalmology, Linkou Medical Center, Chang Gung Memorial Hospital, Taoyuan 333, Taiwan 6 Department of Chemistry, University of Cincinnati, Cincinnati, OH 45221-0172, USA 7 Development Center for Smart Textile, National Taipei University of Technology, Taipei 106, Taiwan Citation: Tessema, E.; Elakkat, V.; * Correspondence: [email protected] (C.-F.C.); [email protected] (P.Z.); Chiu, C.-F.; Zheng, J.-H.; Chan, K.L.; [email protected] (N.L.) Shen, C.-R.; Zhang, P.; Lu, N. † These authors contributed equally to this work. Recoverable Phospha-Michael Additions Catalyzed by a Abstract: Phospha-Michael addition, which is the addition reaction of a phosphorus-based nucle- 4-N,N-Dimethylaminopyridinium ophile to an acceptor-substituted unsaturated bond, certainly represents one of the most versatile and Saccharinate Salt or a Fluorous powerful tools for the formation of P-C bonds, since many different electrophiles and P nucleophiles Long-Chained Pyridine: Two Types can be combined with each other. -

Development of the Interrupted Nazarov Cyclization of Allenyl Vinyl Ketones, with Application to the Total Synthesis of the Cyclooctane Natural Product Roseadione
Development of the Interrupted Nazarov Cyclization of Allenyl Vinyl Ketones, with Application to the Total Synthesis of the Cyclooctane Natural Product Roseadione by Vanessa M. Marx Submitted in partial fulfilment of the requirements for the degree of Doctor of Philosophy at Dalhousie University Halifax, Nova Scotia May 2011 © Copyright by Vanessa M. Marx, 2011 DALHOUSIE UNIVERSITY DEPARTMENT OF CHEMISTRY The undersigned hereby certify that they have read and recommend to the Faculty of Graduate Studies for acceptance a thesis entitled “Development of the Interrupted Nazarov Cyclization of Allenyl Vinyl Ketones, with Application to the Total Synthesis of the Cyclooctane Natural Product Roseadione” by Vanessa M. Marx in partial fulfilment of the requirements for the degree of Doctor of Philosophy. Dated: May 19, 2011 Supervisor: _________________________________ Readers: _________________________________ _________________________________ _________________________________ Departmental Representative: _________________________________ ii DALHOUSIE UNIVERSITY DATE: May 19, 2011 AUTHOR: Vanessa M. Marx TITLE: Development of the Interrupted Nazarov Cyclization of Allenyl Vinyl Ketones, with Application to the Total Synthesis of the Cyclooctane Natural Product Roseadione DEPARTMENT OR SCHOOL: Department of Chemistry DEGREE: PhD CONVOCATION: October YEAR: 2011 Permission is herewith granted to Dalhousie University to circulate and to have copied for non-commercial purposes, at its discretion, the above title upon the request of individuals or institutions. I understand that my thesis will be electronically available to the public. The author reserves other publication rights, and neither the thesis nor extensive extracts from it may be printed or otherwise reproduced without the author’s written permission. The author attests that permission has been obtained for the use of any copyrighted material appearing in the thesis (other than the brief excerpts requiring only proper acknowledgement in scholarly writing), and that all such use is clearly acknowledged. -

1-Alkenylboranes And(E)-1-Alkenylboronates an Investigation of Borane/Nitrone Reactions
W&M ScholarWorks Dissertations, Theses, and Masters Projects Theses, Dissertations, & Master Projects 1991 Preparation and Characterization of (E)-1-Alkenylboranes and(E)-1-Alkenylboronates an Investigation of Borane/Nitrone Reactions Philip Louis Smith College of William & Mary - Arts & Sciences Follow this and additional works at: https://scholarworks.wm.edu/etd Part of the Organic Chemistry Commons Recommended Citation Smith, Philip Louis, "Preparation and Characterization of (E)-1-Alkenylboranes and(E)-1-Alkenylboronates an Investigation of Borane/Nitrone Reactions" (1991). Dissertations, Theses, and Masters Projects. Paper 1539625667. https://dx.doi.org/doi:10.21220/s2-902s-jv27 This Thesis is brought to you for free and open access by the Theses, Dissertations, & Master Projects at W&M ScholarWorks. It has been accepted for inclusion in Dissertations, Theses, and Masters Projects by an authorized administrator of W&M ScholarWorks. For more information, please contact [email protected]. Preparation and characterization of (E)-l-Alkenylboranes and (E)-l-Alkenylboronates And An Investigation of Borane/Nitrone Reactions A Thesis Presented to The Faculty of the Department of Chemistry The College of William and Mary in Virginia In Partial Fulfillment Of the Requirements for the Degree of Masters of Arts by Philip L. Smith 1991 APPROVAL SHEET This thesis is submitted in partial fulfillment of the requirements for the degree of Masters of Arts L Philip L. Smith Approved, September 1991 + W. Gary Hollis, Ph/D. toi/M 6/. David W. ThompsofvPh. D Christopher J. AbeW, Ph.D. DEDICATION For George and Herminia, my parents, Stella and Kimberly, my sisters, and Christain, my brother. iii ACKNOWLEDGMENTS I wish to express my sincere appreciation to Dr. -

Electron Deficient Heterocycle. Examples Abound
Pyridines Pyridines are the most commonly encountered π- electron deficient heterocycle. Examples abound. H O 4 N nifedipine 5 3 N NH2 (anti- angina) H CH3 6 2 MeO2C CO2Me N N 1 N NO2 nicotine niacin (nicitinamide) (in NADP) There are many classical syntheses of pyridines; only a few can be covered in the time available. 1. Hantzsch Synthesis Probably the conceptually simples pyridine synthesis would be a simple extension based on the Paal- Knorr pyrrole synthesis. In other words…. Paal-Knorr NH3 R5 R2 5 2 R N R OO H the shouldn't a 1,5-dicarbonyl do.... NH3 [O] 6 2 6 2 R R 6 2 R N R O O R N R H This is absolutely feasible. Furthermore, as you might expect, the 1,5-dicarbonyls are readily accessible by Michael reaction chemistry (1,4-, conjugate additions). The one- pot version of this, where the unsaturated carbonyl is prepared, the Michael reaction occurs, and the pyridine formation is accomplished, is quite common. It is called the Hantzsch synthesis. 4 O O 4 R O NH3 or O R O EtO2C CO2Et R4 NH4OAc EtO + + OEt EtO OEt ∆∆∆ H2O, O O O O OO ** R4 R4 FeCl3 EtO2C CO2Et EtO2C CO2Et ∆∆∆ H2O, N N H It’s rather forceful conditions, but the ester groups can be decarboxylated. The shown example is a symmetric case, but unsymmetrical ones can be done by doing the aldol condensation (here called a Knoevenagel) first, discretely, and then putting that compound (** ) into a separate reaction doing the subsequent steps. -
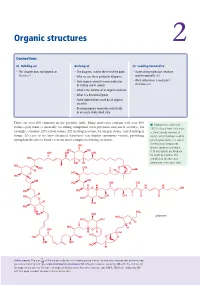
Organic Structures 2
Organic structures 2 Connections Building on Arriving at Looking forward to • This chapter does not depend on • The diagrams used in the rest of the book • Ascertaining molecular structure Chapter 1 • Why we use these particular diagrams spectroscopically ch3 • How organic chemists name molecules • What determines a molecule’s in writing and in speech structure ch4 • What is the skeleton of an organic molecule • What is a functional group • Some abbreviations used by all organic chemists • Drawing organic molecules realistically in an easily understood style There are over 100 elements in the periodic table. Many molecules contain well over 100 ■ Palytoxin was isolated in atoms—palytoxin (a naturally occurring compound with potential anticancer activity), for 1971 in Hawaii from Limu make example, contains 129 carbon atoms, 221 hydrogen atoms, 54 oxygen atoms, and 3 nitrogen o Hane (‘deadly seaweed of atoms. It’s easy to see how chemical structures can display enormous variety, providing Hana’), which had been used to enough molecules to build even the most complicated living creatures. poison spear points. It is one of the most toxic compounds OH known, requiring only about HO OH 0.15 micrograms per kilogram OH OH OH for death by injection. The HO complicated structure was O OH H determined a few years later. HO OH OH O H H O O HO HO H OH OH HO OH OH H H H H O N N OH HO HO H HO OH OH O O O HO OH H OH HO OH NH2 HO OH HO palytoxin HO OH O H HO H OH O H H H HO HO OH O O OH OH HO H Online support.